Дополнение множества
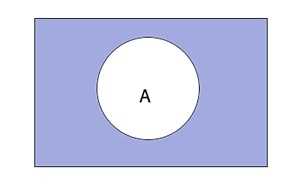
Дополнением к множеству A является множество \(\overline A\), которое состоит из элементов, не входящих в А.
\(\overline A\;=\;\left\{x\;\vert\;x\;\not\in\;A\right\}\)
При этом не все элементы, не являющиеся элементами А, могут быть включены в \(\overline A.\) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение \overline A определяется следующим образом:
\(\overline A\;=\;U\;\backslash\;A\)
Таким образом выглядит дополнение \(\overline A\) графически:
Решение задач, примеры
Круги Эйлера и как решать сложные логические задачи, используя свойства диаграммы, можно показать на примерах.
Задача 1. Пусть имеется следующее условие: 54 школьника шестых классов занимаются в авиамодельном, музыкальном и танцевальном кружках. Каждый посещает хотя бы один кружок. Музыкой занимаются 32 ученика, 22 — танцами, 34 — авиамоделированием. Участвуют в музыкальном и танцевальном кружках 11 школьников, в музыкальном и авиамоделировании — 21, в танцевальном и авиамоделировании — 12. Сколько учащихся посещают все три кружка?
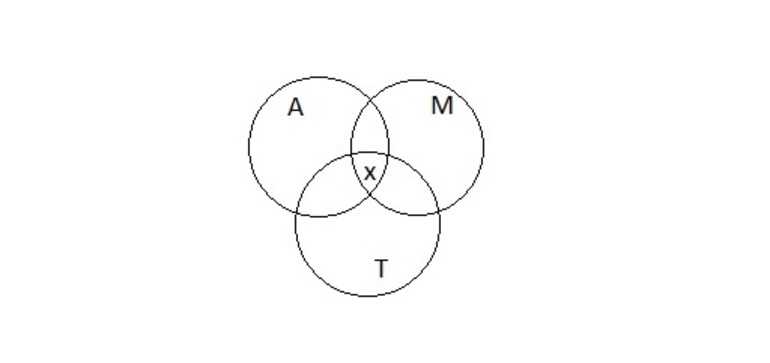
Рисунок 2
Проект решения предполагает необходимость расписать всех 54 школьников в соответствии с условиями задачи. Известно, что в авиамодельном кружке 34 ученика. Если прибавить к этому число учеников, которые занимаются музыкой, их 32 человека, то получится A ⋃ M, где ⋃ обозначение объединения множеств, будет состоять из 34 + 32… учеников.
Но при взгляде на круги Эйлера (Рисунок 2) становится понятно, что те, кто занимается и музыкой, и авиамоделированием посчитаны дважды. Это область на диаграмме, которая принадлежит и кругу A, и кругу М, таких учеников 21. Значит, объединение множеств A ⋃ M будет 34 + 32 — 21…
Теперь нужно прибавить 22 школьника, занимающихся танцами. A ⋃ M ⋃ T равно 34 + 32 — 21 + 22… Тут опять некоторые ученики оказываются посчитаны дважды. Можно вычесть из общей суммы тех, кто занимается танцами и музыкой — 11 человек и 12 человек, участвующих в авиамодельном и танцевальном кружках одновременно. Функция принимает следующий вид: A ⋃ M ⋃ T будет 34 + 32 — 21 + 22 — 11 — 12…
Но при этом школьники, которые посещают все три кружка, оказались отняты дважды. Их число обозначено x и его надо прибавить один раз к имеющейся формуле. Чтобы решить задачу, требуется определить x из полученного уравнения (Рисунок 3).
54 = 34 + 32 — 21 + 22 — 11 — 12 + х; откуда следует, что x = 10. Ответ: 10.
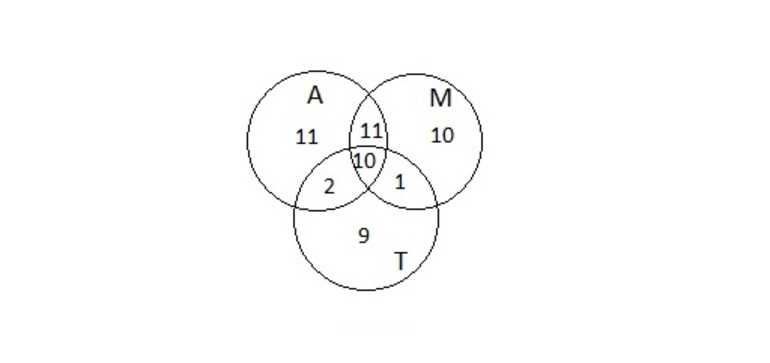
Рисунок 3
Задача 2. В школьную библиотеку пришло 30 учеников седьмого класса. Из них 15 человек взяли учебник по алгебре, 12 — по русскому языку, 10 человек не взяли ни одного учебника. Сколько учеников получили учебники по алгебре и русскому языку?
Множества на диаграммах представлены на рисунке 4. В большом круге 30 учеников, внутри двух малых 30 — 10 = 20 человек. По условию задачи 15 учеников получили учебник по алгебре, значит, 20 — 15 = 5 учеников получили только учебник по русскому языку. А в условии говорится, что 12 человек взяли учебник по русскому, то есть 12 — 5 = 7 школьников получили учебники и по алгебре, и по русскому. Ответ: 7.
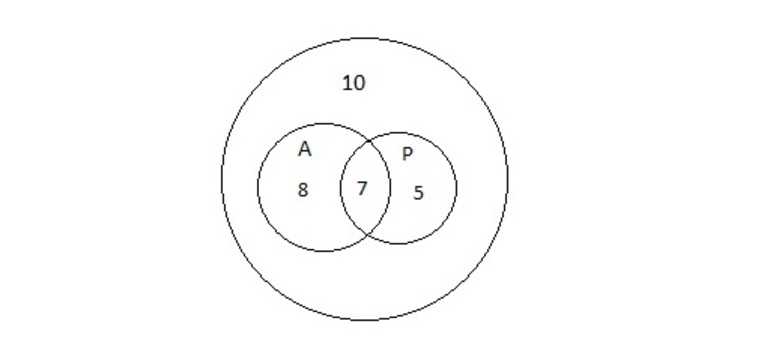
Рисунок 4
Круги Эйлера часто применяются для решения самых разных задач. Они служат для развития способности к логическому мышлению у дошкольников. Большой раздел задач для школьников может решаться с помощью диаграмм. Многие учёные в своих исследованиях тоже обращаются к этому методу, который повышает наглядность решаемых проблем и помогает в их обдумывании. Использование простых фигур позволяет свести решение любой сложной задачи к символической логике и упростить ход рассуждений. Диаграммы могут применяться и в обычной жизни, например при поиске работы. Пересечение кругов «лучше всего получается», «больше всего нравится делать» и «чем можно заработать», возможно, даст нужный результат.
Решение задач с помощью кругов Эйлера
Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.
Задача про любимые мультфильмы
Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».
Решение:
Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:
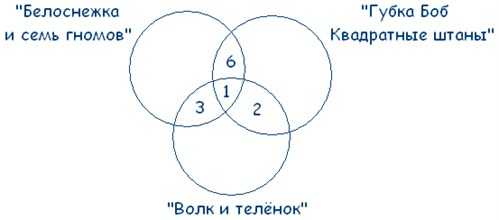
Выходит, что:
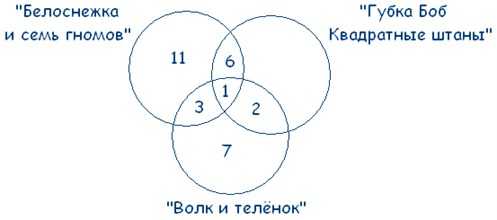
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Теперь смело можем сложить все полученные цифры и выяснить, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.
А еще давайте рассмотрим задачу
, которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор
?
Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
Опираясь на условия задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор
(обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.
Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
Принцип кругов Эйлера
Помни про эмблему из «Зачарованных», она тебе понадобится для визуализации.

Круги Эйлера в реальной жизни
На самом деле, все гениальное просто и самая лучшая и простая техника с техникой Эйлера называется «три круга». Для использования этой несложной техники тебе понадобится три карандаша разного цвета и листок бумаги. Ловкость ума и никакого мошенничества, честно слово! Сейчас ты научишься мыслить ещё более рационально, чем до этого момента!
Помни, что один круг–один инструмент. Например: «что я люблю делать?», «что у меня получается лучше всего?», «как из этого извлечь выгоду или заработок?».
Рисуй круги.
Тут нам и понадобится эмблема из нашумевшего сериала. Нарисуй три круга (у каждого круга свой цвет), так, чтобы круги пересекались образовывая внутри трилистник.
Дай кругам названия.
Название круга – это инструмент, присвой каждому кругу свой. Раскрой полностью смысл каждого инструмента. Что-то нравится? Напиши почему нравится. Напиши о том, сколько ты хочешь зарабатывать, укажи причину – поставь себе цель. Напиши, почему у тебя получается делать что-то лучше, чем остальные, похвали себя.
Очень важно рисовать круги до тех пор, пока не образуется этот трилистник. Да, круги могут не пересекаться, тогда нужно думать, как сделать так, чтобы пересеклись, может быть, придётся заменять инструменты
Круги могут быть разного размера, фигура внутри не обязательно должна иметь равные части, самое главное, чтобы эти части были.
Теперь, когда ты нарисовала круги, распределила задачи, в самом центре появилась фигура похожая на треугольник–эта фигура является главным отношением между твоими «подмножествами», она даёт конечный результат. Получившиеся листки – это путь к конечному результату.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
\(n(U)\;=\;100\\n(Р)\;=\;28,\;n(Ф)\;=\;42,\;n(К)\;=\;30\\n\;(Р\;\cap\;Ф)\;=\;10,\;n(Р\;\cap\;К)\;=\;8,\;n\;(Ф\;\cap\;К)\;=\;5\\n\;(Р\;\cap\;Ф\;\cap\;К)\;=\;3\)
Необходимо найти \(n(Р\;\cup\;Ф\;\cup\;К)\;=\;n\;(U\;\backslash\;(Р\;\cap\;Ф\;\cap\:К))\)
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна
Составляя ее, важно помнить, что если в \(Р\;\cap\;Ф\;\cap\:К\) три элемента, а в множестве \(Р\;\cap\;Ф\) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено
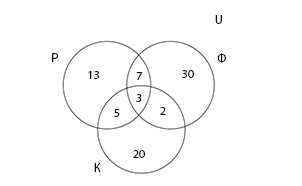
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
\(n(Р\;\cup\;Ф\;\cup\;К)\;=\;13\;+\;7\;+\;30\;+5\;+\;3\;+\;2\:+\;20\;=\;80\)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
\(n(U\;\backslash\;(Р\;\cup\;Ф\;\cup\;К))\;=\;100\;-\;80\;=\;20\)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
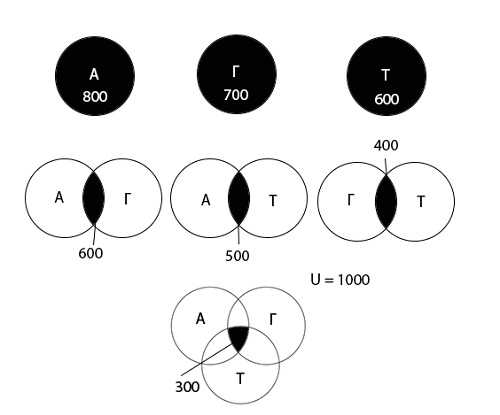
Теперь используя диаграмму, обозначим область, которую необходимо найти:
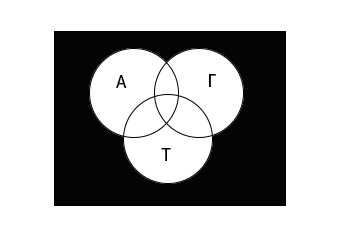
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
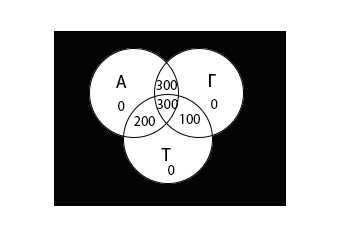
Определим x:
\(x\;=\;U\;-\;(A\;\cup\;Г\;\cup\;Т)\;\)
При U — универсум
U = 1000
\((A\;\cup\;Г\;\cup\;Т)\;=\; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900\)
x = 1000 — 900 = 100
Практическое применение
Немецкий математик XVIII в. Леонард Эйлер внес большой вклад в развитие прикладных наук. Помимо огромного количества работ, он представил графическую модель-схему представления пересечения категории которые, которые позже назвали кругами Эйлера. Эта методика помогает в поиске и более наглядном отображении логических связей между множествами, а также разными явлениями, понятиями и отношениями. Можно визуализировать любые рассуждения, чтобы быстрее найти ответы на вопросы.
Изобретение Эйлера имеет прикладное значение. Наглядный способ помогает в решении логической или математической задачи. Однако методика вышла далеко за пределами математик. Круги Эйлера в своих работах использовали такие ученые, как Джон Венн, Эрнест Шредер и другие.
Сегодня диаграммы ученого используют не только математика, логика и информатика, но практически все науки. В том числе и психология. Ведь геометрический шаблон может использоваться для решения жизненных проблем, познания себя, своих желаний и возможностей.
В психология вообще активно применяются разные методики-изображение целей и желаний. Например, отлично работает визуализация, призванная помогать в достижении цели. Визуализация – это перевод мысленных представлений в зрительные образы, размышление у себя в голове с целью их физического воплощения. Но если визуализация – это, скорее, сила воображения, то с кругами все сводится к логике и математическим расчетам. Хотя и там, и там работает наглядность.
Достаточно даже трех кругов, чтобы решить какую-то проблему или что-то узнать. Кругов может быть больше: четыре, шесть, десять. Хотя много не надо. Смысл методики не в количестве кругов, а в их пересечении. И пусть они работают по одной схеме, но ведь дают абсолютно разные и нередко неожиданные результаты.
Иногда вместо круга используется треугольник или прямоугольник. Вообще, элемент может быть любой. Просто круги или овалы лучше всего подходят под условие метода.
Например, можно задать вопрос о профессии. Каждый круг или овал – один вопрос-задача: что я умею делать, что хочу, сколько зарабатываю и сколько хочу и т.д. Вопрос нужно написать в самой фигуре или рядом с ней. Причем какая-то фигура может не пересекаться с другой. Когда рисунок закончен, становиться намного понятнее решение проблемы.
Похожая техника – капля в луже. Вообще, на основе кругов немецкого математика изобретено множество похожих методик. Какие-то практически полностью повторяют эйлерские диаграммы, некоторые похожи содержанием. Главное, что что-то (мысль, идея, запрос) должны изображаться.
Обычно «капля в луже» применяется для диагностики психоэмоционального состояния человека. Рисунок представляет собой как бы круги на воде. В центре сам человек, а каждый следующий круг может представлять качество характера или какое-то явление, характеризующее его состояние. Например, как он реагирует на стресс, какими ресурсами обладает, чтобы справиться с ситуацией, как чувствует себя вне зоны комфорта и т.п.
Круговой методикой тоже полезно пользоваться для решения каких-либо проблем. Это еще одна своеобразная визуализация или представление проблемы. А рисование кругов напоминает геометрическую схему Эйлера с той лишь разницей, что здесь фигуры не пересекаются.
Многие компании используют этот метод для психологической диагностики сотрудников. Круги Эйлера также помогают справиться с негативом на работе. Например, с их помощью можно взвесить плюсы и минусы разной деятельности и найти оптимальный вариант ее выполнения.
Иногда у сотрудников такой объем работы, с которым, кажется, невозможно справиться. Разделить задания тоже можно, использую диаграмму немецкого математика. Наглядно и просто.
Круги Эйлера хороши тем, что их может использовать абсолютно любой человек в любом возрасте: ребенок в первый год жизни (с помощью родителей, конечно), дошкольник, студент, женщина или мужчина, начальник и подчиненный, профессор и домохозяйка. Например, дети, используя эту методику, могут научиться разделять множество и подмножество. Взрослые делать более сложный выбор. И это необязательно решение математической задачи, но также и психологической дилеммы.
Кто-то решает рисунками глобальные задачи, а кто-то просто весело проводит время. Ведь круги можно применять даже в быту, хоть для расчета рецепта блюда, оптимального времени уборки или какими растениями лучше засадить сад. Почти для этого математик и придумал технику – чтобы упрощать жизнь.
Где применяются круги Эйлера
Круги Эйлера широко используются во многих упражнениях на мышление и логику. Ученые сами применяют этот метод для решения сложных математических задач. Это объясняется тем, что простая форма схемы упрощает рассуждения и позволяет визуализировать возможные решения.
Сегодня круги Эйлера широко используются в его работе: круг Эйлера — это простая форма, которую можно использовать для визуализации решения сложной математической задачи.
Основным преимуществом этого метода является его гибкость. Развитие детского мышления и сложных математических (и не только!) способностей. проблемы.
Отношения между понятиями
Логические операции, разрешающие доказывать утверждения и делать выводы, основаны на связях и отношениях разных понятий. При классификации понятия делятся на сравнимые, между которыми существуют логические связи и отношения, и несравнимые, которые не имеют связей. К несравнимым относятся, например, «машина» и «квадрат», «озеро» и «клетка». У них нет общих элементов и их нельзя сравнивать.
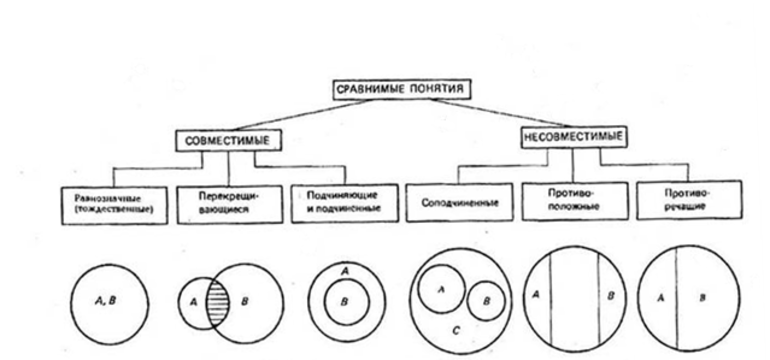
Рисунок 1
Сравнимые понятия подразделяются на совместимые и несовместимые. Совместимые понятия отличаются тем, что имеют хотя бы один общий элемент:
- равнозначные (тождественные);
- перекрещивающиеся;
- подчиняющие и подчинённые.
У равнозначных понятий объёмы полностью совпадают. Например, А — писатель Чехов, В — автор пьесы «Вишнёвый сад». Графически тождественность можно представить как два круга, слившиеся в один (Рисунок 1).
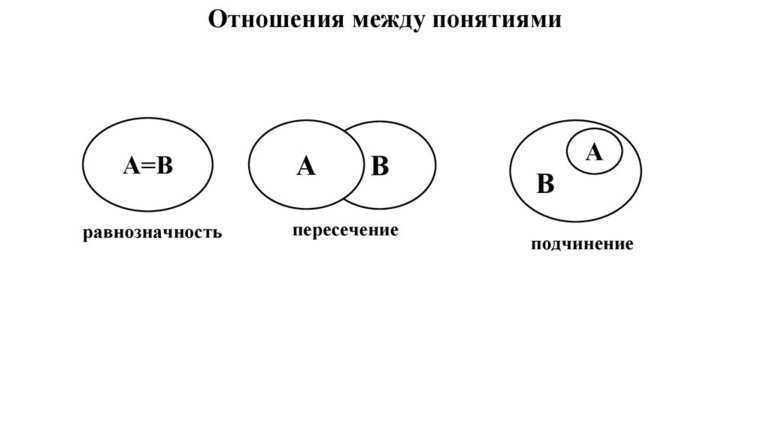
Пересекающимися понятиями, или находящимися в отношении перекрещивания, считаются те, объёмы которых совпадают частично. Пример: A — «математик», B — «репетитор»; A — «студент», B — «спортсмен». Часть объёма понятия «математик» входит в объём понятия «репетитор» и наоборот.
Понятия, состоящие в отношении подчинения, содержат одинаковые элементы, а объём подчинённого целиком входит в объём подчиняющего. Например, «млекопитающее» и «коза».
Несовместимыми называют понятия, не имеющие общих элементов:
- соподчинённые;
- противоположные;
- противоречащие.
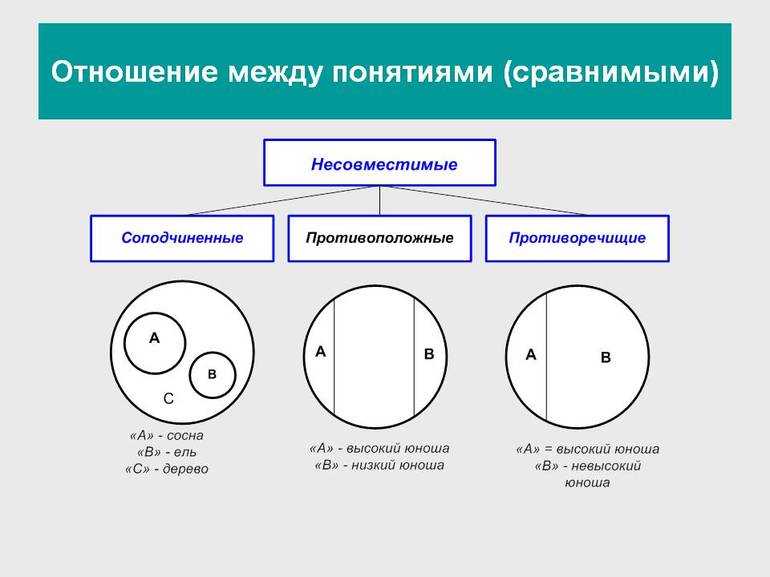
Соподчинённые понятия имеют общие элементы и вместе входят в родовое понятие, но в их объёмах общие элементы отсутствуют. Например, А — «корова», B — «овца», C — «млекопитающее». Круги A и B необходимо поместить внутри круга, изображающего объём понятия C, но они не смогут пересекаться, так как не бывает млекопитающих, которые были бы и коровой, и овцой одновременно.
Противоположные понятия — это виды одного и того же рода, но одно из них имеет какой-то признак, а другое не обладает им и содержит признак, несовместимый с первым, направленный против него. Таковы A — «большой дом» и B — «маленький дом». Тут в отличие от отношения противоречия возможны предметы, которые не входят ни в A и ни в B. Если общее родовое C — дом, то в его круге будут изображения двух сегментов A и B, расположенных напротив друг друга, а оставшаяся часть должна соответствовать всем остальным домам (средним, меньше средних).
Что даёт построение кругов
Когда ты начнёшь использовать схему в деле, применяя техники и возьмёшь это за правило, твоё мышление натренируется, и ты станешь понимать этот мир лучше, найдёшь своё предназначение.

Фото Mel Poole on Unsplash
Разовьётся логическое мышление, ты станешь продуктивнее и рациональнее мыслить.
Да, пересечение «трёх кругов» порой даёт отрицательный результат, ты можешь даже по началу расстроиться от того, что тебя это не устроит. Но тебе нужно понимать, что не все тебе по силам, нет на свете совершенных людей, которые могут по щелчку пальца сделать так, как надо им. У тебя попросту может быть другая цель, которую ты не ощущаешь, потому что она находится глубоко в подсознании. Круги Эйлера как раз и предназначены для того, чтобы найти себя с помощью логики и размышлений, которые распространяются на все аспекты жизни.
Техники универсальны, они подойдут абсолютно для всех аспектов жизни: от бытовых мелочей до глобальных целей в жизни. Просто меняй инструменты, применяя техники и жизнь будет становится проще. Главное – это тренировки. Удачи в поиске себя!
16.
Ч
е
р
т
с
И
х
м
ы
ы
в
н
о
ь
н
Л
о
е
т
Д
а
м
и
и
м
н
а
а
ч
з
а
д
П О Н Я Т И Е
Каждый предмет или явление обладает
некими свойствами (признаками).
Получается, что составить понятие об
объекте означает, прежде всего, умение
отличить его от других сходных с ним
объектов.
Можно сказать, что понятие – это мысленное
содержание слова.
Понятие
– это форма мысли, отображающая предметы
в их наиболее общих и существенных
признаках*.
Понятие – это форма мысли, а не форма
слова, так как слово лишь метка, которой
мы помечаем ту или иную мысль.
Слова могут быть различны, но при этом
обозначать одно и то же понятие. По-русски
– «карандаш», по-английски – «pencil»,
по-немецки –bleistift. Одна
и та же мысль в разных языках имеет
разное словесное выражение.
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ
ЭЙЛЕРА.
Понятия, имеющие в своих содержаниях
общие признаки, называются СРАВНИМЫМИ
(«адвокат» и «депутат»; «студент» и
«спортсмен»).
В противном случае, понятия считаются
НЕСРАВНИМЫМИ
(«крокодил» и «блокнот»; «человек» и
«пароход»).
Если кроме общих признаков понятия
имеют и общие элементы объёма, то они
называются СОВМЕСТИМЫМИ
.
Существует шесть видов отношений между
сравнимыми понятиями. Отношения между
объёмами понятий удобно обозначать с
помощью кругов Эйлера (круговые схемы,
где каждый круг обозначает объём
понятия).
|
ВИД |
ИЗОБРАЖЕНИЕ |
|
РАВНОЗНАЧНОСТЬ Объёмы понятий полностью совпадают. Т.е. это |
1) А – Аристотель В – основатель логики 2) А – квадрат В – равносторонний прямоугольник |
|
ПОДЧИНЕНИЕ Объём одного понятия полностью входит |
1) А – человек В – студент 2) А – животное |
|
ПЕРЕСЕЧЕНИЕ Объёмы двух |
1) А – юрист В – депутат 2) А – студент В – спортсмен |
|
СОПОДЧИНЕНИЕ Понятия, не |
1) А – животное В – кот; С – 2) А – драгоценный В – золото; С D- платина |
|
ПРОТИВОПОЛОЖНОСТЬ Понятия А |
1) А – белый кот; В – (коты 2) А – горячий чай; (чай может быть Т.е. понятия А и В не исчерпывают всего |
|
ПРОТИВОРЕЧИЕ Отношение |
1) А – высокий дом В – невысокий 2) А – выигрышный В – невыигрышный Т.е. понятия А и не-А исчерпывают весь |
Упражнение:
Определите вид
отношений по объёму приведённых ниже
понятий. Изобразите их с помощью кругов
Эйлера.
1)
А – горячий чай; В – холодный чай;
С – чай с лимоном
Горячий чай (В) и холодный чай (С) –
находятся
в отношении противоположности.
Чай с лимоном (С) может быть как горячим,
так и холодным, но может быть и, например,
тёплым.
2)
А
– деревянный;В
– каменный;С
– строение;D
–
дом.
Всякое ли строение (С) – дом (D)?
– Нет.
Всякий ли дом (D) – строение
(С)? – Да.
Что-то деревянное (А) обязательно ли дом
(D) или строение (С) – Нет.
Но можно найти деревянное строение
(например, будка),
также можно найти деревянный дом.
Что-то каменное (В) не обязательно дом
(D) или строение (С).
Но может быть и каменное строение, и
каменный дом.
3)
А
– российский город;В
– столица
России;
С
– Москва;D
–
город на Волге;Е
– Углич.
Столица России (В) и Москва (С) – один и
тот же город.
Углич (Е) является городом на Волге (D).
При этом, Москва, Углич, как и любой город
на Волге,
являются российскими городами (А)
При решении многих задач, связанных с множествами, незаменимым оказывается приём, основанный на использовании так называемых «кругов Эйлера». Эти диаграммы впервые появились в работах одного из величайших математиков в истории Леонарда Эйлера, который в течение продолжительного времени жил и работал в России и был членом Петербургской академии наук. Использование кругов Эйлера добавляет наглядности при решении сложных задач, делая многие вещи буквально очевидными. Предлагаю вам в этом убедиться самостоятельно на примере решения следующей задачи.
Техника «капля в луже»
Эта техника подходит для тебя, если ты не можешь определить свои качества.

Фото автора Jana Kukebal: Pexels
Для этого нужно представить себя каплей, которая, попадая в воду даёт множество кругов.
Обозначь себя главным кругом. Далее подобно капле в луже рисуй круги вокруг себя, делая их все больше и больше. Нарисуй минимум пять кругов и обозначь их своими качествами, прислушиваясь к себе. Самый первый круг определяет тебя, последующие же помогают идти по жизни.
Рисуя такие круги, ты находишь в себе те качества, о которых даже не подозревала, они помогут раскрыть твоё потенциал. Если вдруг тебе не нравится какое-то качество в себе, ты можешь проработать этот момент и избавиться от того, что тебе не нравится. Главная задача техники–это понять, какие качества в тебе вообще есть.
Отношения между множествами
Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).
Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств – строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.
В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х 2 = -5.
Описание схемы кругов Эйлера
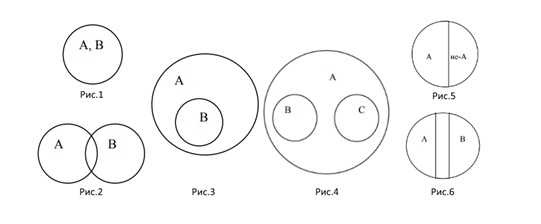
Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.
Делятся на группы, в зависимости от типа отношений между множествами:
- равнозначные (рис.1);
- пересекающиеся (рис.2);
- подчиненные (рис.3);
- соподчиненные (рис.4);
- противоречащие (рис.5);
- противоположные (рис.6).
Типовой пример такой диаграммы:
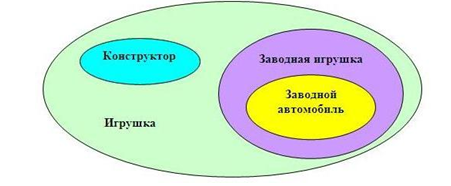
Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.
Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».
Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».
При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.
Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.
Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.






























