§ 5.6. энергия электромагнитной волны

Переменный ток. Производство, передача и потребление электрической энергии

Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.

Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:

• мгновенное значение силы тока – i;

• мгновенное значение напряжения – u;

• амплитудное значение силы тока – Im;

• амплитудное значение напряжения –Um.

Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.

Активное сопротивление

Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ​\( R \)​. (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.

В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:

Мгновенное значение мощности: ​\( p=i^2R, \)​

среднее значение мощности за период: ​\( \overline{p}=\frac{I_m^2R}{2}. \)​

Действующим значением силы переменного тока ​\( I_Д \)​ называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:

Действующим значением напряжения переменного тока ​\( U_Д \)​ называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:

Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.

Индуктивное сопротивление

Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ​\( \pi/2 \)​. Колебания силы тока и напряжения происходят по закону:

Амплитуда силы тока в катушке:

где ​\( L \)​ – индуктивность катушки.

Индуктивным сопротивлением ​\( X_L \)​ называют физическую величину, равную произведению циклической частоты на индуктивность катушки:

Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.

Для цепи с индуктивным сопротивлением выполняется закон Ома.

Плотность импульса электромагнитной волны

При поглощении в веществе какого-нибудь тела электромагнитная волна оказывает на это тело давление, то есть сообщает ему импульс. Если обозначить плотность импульса как $\overrightarrow{G}$, то его можно определить, используя вектор Умова — Пойнтинга ($\overrightarrow{P}$):

Пусть плоская волна падает перпендикулярно на плоскую поверхность тела. Положим, что $\varepsilon =1,\ \mu =1$ плохо проводящего тела. Электрическое поле волны будет возбуждать в теле ток, плотность которого ($\overrightarrow{j}$):

$\sigma $ — удельная проводимость вещества. Магнитное поле волны действует на данный ток с удельной силой (${\overrightarrow{F}}_u$) (силой на единицу объема):

Направление ${\overrightarrow{F}}_u$ совпадает с направлением распространения волны.

При этом поверхностному слою тела толщиной $\triangle l$, единичной площади волной сообщается импульс за $1 с$, ($\overrightarrow{j}\bot \overrightarrow{H}$) равный:

В том же слое за $1 с$ поглощается энергия:

которая выделяется потом, как тепло. Найдем отношение импульса (10) к энергии (11), имеем:

Воспользуемся выражением (3) при $\varepsilon =1,\ \mu =1,$ получим:

Подставим (13) в формулу (13):

Из выражения (14) следует, что электромагнитная волна, обладающая энергией $W$, имеет импульс ($G$):

Из формулы (15) получаем, что плотность импульса ($G_u$) — импульс единицы объема равен:

Воспользовавшись вектором Умова — Пойнтинга, можно выражение (16) представить как:

В формуле (17) учтено, что направление вектора импульса электромагнитной волны имеет такое же направление, что и вектор Умова — Пойнтинга.

Пример 1

Задание: Какое давление ($p$), производит плоская электромагнитная волна на тело? Она распространялась в вакууме, вдоль $оси X$, падает на тело перпендикулярно, поглощается полностью. Амплитуда напряженности магнитного поля равна $H_m$.

Решение:

В качестве основы для решения задачи примем вывод из теории Максвелла о том, что, если волна падает на тело перпендикулярно его поверхности и полностью поглощается, то:

\

где $\left\langle w\right\rangle $ — средняя объемная плотность энергии электромагнитной волны.

Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:

\ \

Плотность энергии электромагнитного поля ($w$) является суммой плотности электрического поля ($w_E$) и плотности магнитного поля ($w_H$):

\

где:

\

При этом для электромагнитной волны мы имеем соотношение между мгновенными значениями характеристик полей:

\

Следовательно, можем записать следующее:

\

Используем выражение (1.3), подставив вместо H выражение, которое находится в правой части, получим:

\

Найдем среднее от объемной плотности энергии электромагнитной волны, получим:

\

Примем во внимание, что:

\

Тогда формула (1.9) будет переписана как:

\

Ответ: $p=\frac{\mu {\mu }_0{H_m}^2}{2},\ где\ \mu =1\ .$

Пример 2

Задание: Чему равна средняя (по времени) плотность импульса электромагнитной волны ($\left\langle G_u\right\rangle $)? Если электромагнитная волна плоская, распространяется в вакууме по оси X, амплитуда ее магнитного поля равна $H_m.$

Решение:

За основу решения задачи примем формулу:

\\to G_u=\frac{1}{c^2}EH\to \left\langle G_u\right\rangle =\frac{1}{c^2}\left\langle EH\right\rangle \left(2.1\right).\]

Используя соотношение:

\

найдем амплитуду электрического поля:

\

Уравнения колебаний модулей векторов напряженностей электрического и магнитного полей запишем в соответствии с гармоническими законами:

\ \

Подставим выражения (2.3), (2.4) и (2.5) в формулу (2.1), получим:

\

Ответ: $\left\langle G_u\right\rangle =\frac{60 \pi}{c^2}{H_m}^2.$

Свойства электромагнитных волн

Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.

Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.

Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.

Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд

Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.

Электромагнитная волна называется монохроматической, если векторы ​\( \vec{E} \)​ и \( \vec{B} \)​ совершают гармонические колебания с одинаковой частотой (частотой волны).

Длина электромагнитной волны: ​\( \lambda=cT=\frac{c}{\nu}, \)​

где ​\( c \)​ – скорость электромагнитной волны, ​\( T \)​ – период, ​\( \nu \)​ – частота электромагнитной волны.

Свойства электромагнитных волн

• В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·108 м/с.
• Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
• Электромагнитная волна переносит энергию в направлении распространения волны.

Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме. Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени

Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.

Обозначение – ​\( I \)​, единица измерения в СИ – ватт на квадратный метр (Вт/м2).

Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты. Электромагнитная волна обладает общими для любых волн свойствами, это:

Электромагнитная волна обладает общими для любых волн свойствами, это:

• отражение,
• преломление,
• интерференция,
• дифракция,
• поляризация.

Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.

Электромагнитное поле

Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.

Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.

Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.

Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.

Если электрический заряд покоится, то вокруг него существует только электрическое поле.

Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.

Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.

Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.

При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.

Плотность потока энергии волны. Интенсивность волны

Распространение волн всегда связан с переносом энергии, который количественно характеризуется потоком энергии Ф, плотностью потока энергии J и интенсивностью волны I.

Рассмотрим волну, распространяющуюся вдоль оси о х со скоростью v (рис.210). Волна за время A t распространяется на расстояние, равное v • A t. Построим параллелепипед с основаниями A S, перпендикулярными оси ох, и длиной v — At.

Вся энергия волны, заключённая в параллелепипеде, за интервал времени A t пройдёт через правое основание A S. Обозначим энергию, переносимую волной сквозь площадку A S, через A W. Она равна произведению объёмной плотности полной энергии со _пол волны на объём параллелепипеда А V.,

Если объём V,, параллелепипеда мал, то объёмную плотность энергии со _пол волны можно считать одинаковой во всех точках рассматриваемого объёма.

Количество энергии, переносимое волной за единицу времени через поверхность AS, расположенную перпендикулярно направлению распространения волны, называется потоком Ф энергии волны

Поток энергии Ф в системе СИ измеряется в ваттах

(7 Вт =1 Л ж ). Поток энергии Ф волны может изменяться от одной

точки среды к другой. В этом случае используется векторная величина, называемая вектором плотности потока энергии J. Он был введён в 1874 г. профессором Московского университета Н. А. Умовым, поэтому назван вектором Умова.

Вектор Умова (вектор плотности потока энергии J) численно равен энергии, переносимой волной через единичную площадку, расположенную перпендикулярно направлению потока энергии в данной точке среды, за единицу времени

Запишем уравнение (20.56) в векторной форме

Вектор Умова, как и объёмная плотность полной энергии со ,_Ю1 волны, может иметь разные значения в разных точках пространства. В рассматриваемой точке среды вектор Умова изменяется со временем по такому же закону, как и объёмная плотность полной энергии со ,_Ю1 волны. Поэтому величина плотности потока энергии У через любую площадку (х = с о п s t), расположенную перпендикулярно направлению распространения волны, со временем периодически возрастает от нуля (У = 0) до максимального значения (У = У _тах).

В теории волн используется понятие среднего значения

плотности потока энергии за период времени Т (Т = xIL) в

где _пош) — среднее за период Т значение объёмной плотности

определённой точке пространства (х = с о п s t), которое назвали интенсивностью волны I

энергии волны в данной точке среды.

Подставим в (20.59) формулу (20.53)

Здесь учли, что среднее значение квадрата синуса за период Т равно 1.

Запишем формулу для интенсивности I волны, принимая во внимание выражение (20.60)

Отсюда следует, что интенсивность I волны прямо пропорциональна квадрату амплитуды А

Когда волна распространяется в трёхмерном пространстве, то поток энергии Ф через произвольную поверхность S определяется по формуле

где d S = п ? d S, п нормаль к поверхности S.

Плотность потока энергии J и интенсивность I в системе СИ

имеют размерность — ватт на квадратный метр | ^ т ].

Проведём две волновые поверхности в виде сфер, с радиусами г; и г₂. Считаем, что энергия волны не поглощается средой, тогда средние значения энергии, проходящей через волновые поверхности, равны

где S/, S₂ — площади сфер радиусами Г/ и г₂. Подставим в (20.62) интенсивности //, 1₂

сократив на р, у, со , получим

Итак интенсивность I сферической волны убывает по мере удаления от точечного источника по закону

где I 00), I (г) — интенсивность волны на расстояниях г = 1 м и произвольном расстоянии г от источника волны. Уравнение (20.65) следует из (20.63) и (20.64), записанных для двух расстояний г = 1 м и г > 1 м.

Зависимость амплитуды А и интенсивности I сферической волны от расстояния г от источника волны объясняются тем, что по мере удаления фронта волны от источника волн в колебательное движение за равные промежутки времени вовлекаются всё возрастающие объёмы среды.

Уравнение сферической волны записывается в виде

где г — расстояние от источника волн до рассматриваемой точки среды.

Интенсивность I и амплитуда А плоской волны, распространяющейся в среде, не поглощающей энергию волны, не изменяются при удалении от источника волн. Это связано с тем, что в колебательное движение за равные промежутки времени вовлекаются равные объёмы среды.

Интенсивность I плоской волны, распространяющейся в поглощающей среде вдоль положительного направления оси о х, изменяется, как и амплитуда волны по экспоненциальному закону

где I () — интенсивность волны в точке х = О, а — линейный коэффициент поглощения упругих волн.

Плотность энергии, которую переносят электромагнитные волны

Электромагнитные волны переносят энергию. Ее объемную плотность ($w$) составляют электрическое и магнитное поля, то есть:

где $w_E$ — плотность энергии электрического поля, $w_m$ — плотность энергии магнитного поля. При этом известно, что:

Для электромагнитной волны выполняется соотношение для мгновенных значений $E$ и $H$:

Из выражений (2) и (3), получается, что:

Иначе можно записать:

Из теории Максвелла следует вывод о том, что если тело полностью поглощает падающую на него перпендикулярно волну, то давление ($p$), которое она производит равно среднему значению объемной плотности энергии в данной волне:

Энергия электрического поля: конденсатор

Конденсаторы обладают способностью накапливать электрический заряд и, следовательно, электрическую энергию. Они входят в состав многих устройств: двигателей, радио- и телевизионных схем, систем освещения автомобилей и многого другого.

Конденсаторы состоят из двух проводов, разделенных небольшим расстоянием. Каждому из них дается заряд одинаковой величины и противоположного знака, создавая электрическое поле в пространстве между обоими проводниками. Геометрия может меняться, как и у плоскопараллельных пластинчатых конденсаторов.

Энергия, хранящаяся в конденсаторе, возникает в результате работы, которая была проделана для его зарядки, что послужило созданию внутри него электрического поля. Путем введения диэлектрического материала между пластинами емкость конденсатора увеличивается и, следовательно, энергия, которую он может хранить.

Конденсатор емкостью C, первоначально разряженный, который заряжается батареей, которая выдает напряжение V, до достижения заряда Q, сохраняет энергию U, определяемую следующим образом:

U = ½ (Q 2 / C) = ½ QV = ½ CV 2

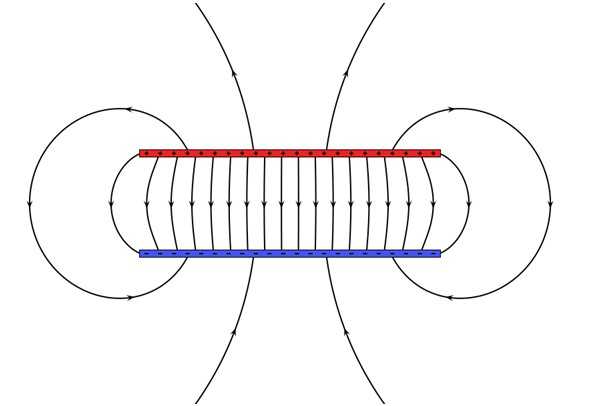
Дипольная антенна

Антенны всюду наполняют пространство электромагнитными волнами. Есть передатчики, которые преобразуют электрические сигналы, например, в радиоволны или микроволны. А есть приемники, которые выполняют обратную работу: они собирают волны и преобразуют их в электрические сигналы.

Давайте посмотрим, как создать электромагнитный сигнал, распространяющийся в космосе, от электрического диполя. Диполь состоит из двух электрических зарядов одинаковой величины и противоположных знаков, разделенных небольшим расстоянием.

На следующем рисунке показано электрическое поле E, когда заряд + находится выше (левый рисунок). E указывает вниз на показанную точку.

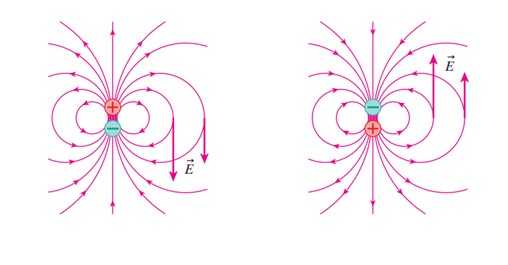
На рисунке 3 справа диполь изменил положение, и теперь буква E направлена ​​вверх. Давайте повторим это изменение много раз и очень быстро, скажем, с частотой f. Таким образом, создается поле E, изменяющееся во времени, вызывающее магнитное поле B , также переменное и имеющее синусоидальную форму (см. Рисунок 4 и пример 1 ниже).

И поскольку закон Фарадея гарантирует, что изменяющееся во времени магнитное поле B порождает электрическое поле, оказывается, что, осциллируя диполь, человек уже имеет электромагнитное поле, способное распространяться в среде.

Обратите внимание, что B поочередно указывает внутрь или наружу экрана (он всегда перпендикулярен E )

Формула и уравнения

Электромагнитные волны — это поперечные волны, в которых электрическое поле E и магнитное поле B перпендикулярны друг другу, а направление распространения волны перпендикулярно полям.

Все волны характеризуются своей частотой. Именно широкий диапазон частот электромагнитных волн дает им универсальность при преобразовании их энергии, которая пропорциональна частоте.

На рисунке 2 изображена электромагнитная волна, в ней электрическое поле E, выделенное синим цветом, колеблется в плоскости zy, магнитное поле B, выделенное красным цветом, колеблется в плоскости xy, а скорость волны направлена ​​вдоль оси + y, согласно показанной системе координат.

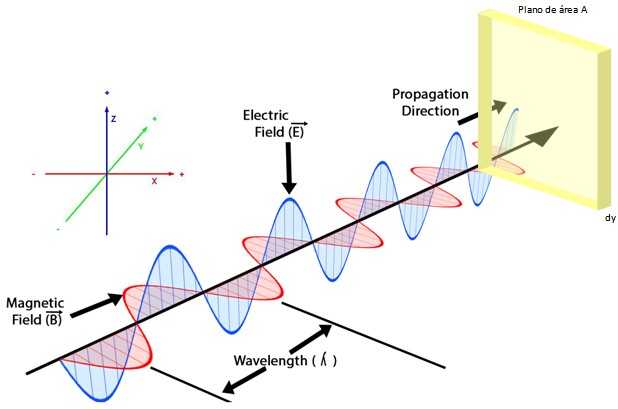
Если на пути обеих волн расположена поверхность, скажем, плоскость площади A и толщины dy, так что она перпендикулярна скорости волны, поток электромагнитной энергии на единицу площади, обозначаемый S, описывается как из вектора Пойнтинга:

Легко проверить, что единицы измерения S — это ватт / м 2 в международной системе.

Есть еще кое-что. Величины полей E и B связаны друг с другом скоростью света c. Фактически, электромагнитные волны в вакууме распространяются так быстро. Это отношения:

Подставляя это соотношение в S, получаем:

Вектор Пойнтинга изменяется во времени синусоидальным образом, поэтому приведенное выше выражение является его максимальным значением, потому что энергия, поставляемая электромагнитной волной, также колеблется, как и поля. Конечно, частота колебаний очень велика, поэтому их невозможно обнаружить, например, в видимом свете.

Вынужденные электромагнитные колебания. Резонанс

Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:

где ​\( \varepsilon \)​ – мгновенное значение ЭДС, \( \varepsilon_m \) – амплитудное значение ЭДС.

При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.

Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.

Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ​\( \varphi_L=-\pi/2 \)​, а на конденсаторе \( \varphi_C=\pi/2 \)​. Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:

Резонансная частота вычисляется по формуле:

Важно!
Резонансная частота не зависит от активного сопротивления ​\( R \)​. Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс

Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ​\( (R\to0) \)​, то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.

График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.

Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.

При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.

Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.

Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.

Гармонические электромагнитные колебания

Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.

В электрических цепях это могут быть колебания:

• силы тока – ​\( i=I_m\cos(\omega t+\varphi+\frac{\pi}{2}); \)​
• напряжения – \( u=U_m\cos(\omega t+\varphi); \)
• заряда – \( q=q_m\cos(\omega t+\varphi); \)
• ЭДС – \( \varepsilon=\varepsilon_m\sin\omega t. \)

В этих уравнениях ​\( \omega \)​ –циклическая частота, ​\( \varphi \)​ – начальная фаза колебаний, амплитудные значения: силы тока – ​\( I_m \)​, напряжения – ​\( U_m \)​ и заряда – ​\( q_m \)​.

Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса

Сила тока равна первой производной заряда от времени:

Амплитуда колебаний силы тока равна:

Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:

Колебания силы тока смещены по фазе относительно колебаний заряда на ​\( \pi/2 \)​.

Период свободных электромагнитных колебаний

Период свободных электромагнитных колебаний находится по формуле Томсона:

где ​\( L \)​ – индуктивность катушки, ​\( C \)​ – электроемкость конденсатора.

Циклическая частота: ​\( \omega=\frac{2\pi}{T}=\frac{1}{\sqrt{LC}} \)​

Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре

При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.

Энергия электромагнитных волн

Предположим, что в поле электромагнитной волны расположена площадка $S$ (рис.1).

Рисунок 1. Площадка, расположенная в поле электромагнитной волны. Автор24 — интернет-биржа студенческих работ

Определим, какая энергия ($W$) переносится электромагнитной волной сквозь эту площадку за малое время ∆t. Построим на основании площадки $S$ параллелепипед, с ребрами параллельными скорости перемещения волны $\vec{v}$. Пусть длины ребер параллелепипеда будут равны $v\Delta{}t$. Объем выделенного параллелепипеда будет:

$\Delta{}V=Sv\Delta{}t\cos{\alpha{}\ \left(1\right),}$

где α – угол между нормалью к площадке $S$ и направлением вектора скорости движения волны. Поскольку за время $\Delta{}t$ волна пробегает расстояние $v\Delta{}t$, то через выделенную нами площадь пройдет искомая нами энергия $W$, которая заключена внутри параллелепипеда.

$W=w\Delta{}V=wSv\Delta{}t\cos{\alpha{}\ \left(2\right),}$

где $w $ – объемная плотность энергии.

Электромагнитная волна имеет две составляющие, которые обладают энергией – это переменное электрическое и магнитное поля, поэтому объемную плотность нашей волны мы запишем как:

$w=\frac{\epsilon{}{\epsilon{}}_0}{2}E^2+\frac{\mu{}{\mu{}}_0}{2}H^2\left(3\right).$

Мы знаем, что напряженности полей в электромагнитной волне связывает уравнение:

$\sqrt{\epsilon{}{\epsilon{}}_0}E=\sqrt{\mu{}{\mu{}}_0}H\left(4\right),$

откуда следует, что мы можем написать:

$w=\epsilon{}{\epsilon{}}_0E^2=\mu{}{\mu{}}_0H^2=\sqrt{\epsilon{}\mu{}}\sqrt{{\epsilon{}}_0{\mu{}}_0}EH\left(5\right).$

Принимая во внимание, что скорость распространения электромагнитной волны в веществе можно представить как:

$v=\frac{1}{\sqrt{\epsilon{}\mu{}{\epsilon{}}_0{\mu{}}_0}}\left(6\right),$

учитывая формулу (5) из выражения (2) следует, что искомая энергия равна:

$W=\sqrt{\epsilon{}\mu{}}\sqrt{{\epsilon{}}_0{\mu{}}_0}EHS\frac{1}{\sqrt{\epsilon{}\mu{}{\epsilon{}}_0{\mu{}}_0}}\Delta{}t\cos{\alpha{}=EHS\Delta{}t\cos{\alpha{}}\left(7\right).}$

Свободные электромагнитные колебания. Колебательный контур

Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.

Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.

Сопротивление катушки ​\( R \)​ равно нулю.

Если зарядить конденсатор до напряжения ​\( U_m \)​, то в начальный момент времени ​\( t_1=0 \)​, напряжение на конденсаторе будет равно ​\( U_m \)​. Заряд конденсатора в этот момент времени будет равен ​\( q_m=CU_m \)​. Сила тока равна нулю.

Полная энергия системы будет равна энергии электрического поля:

Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.

Ток достигает своего максимального значения ​\( I_m \)​ в момент времени ​\( t_2=T/4 \)​. Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.

Полная энергия системы в этот момент времени равна энергии магнитного поля:

В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.

В момент времени ​\( t_3=T/2 \)​ заряд конденсатора равен ​\( q_m \)​, напряжение равно ​\( U_m \)​, сила тока равна нулю.

Полная энергия системы равна энергии электрического поля конденсатора.

Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.

В момент времени ​\( t_4=3T/4 \)​ сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.

Через время, равное периоду ​\( T \)​, система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.

Важно!Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре

В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:

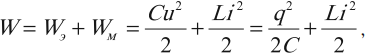
где ​\( i, u, q \)​ – мгновенные значения силы тока, напряжения, заряда в любой момент времени.

Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.