Контур с током в магнитном поле

Плотность энергии электрического и магнитного полей

Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.

В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.

Формула 12

Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:

\({\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}\)

где \(U=\int E\,dx\) — разность потенциалов, или напряжение.

Формула 13

Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:

\({\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}\)

где \(I(t)={dQ \over dt}\) — сила тока.

Формула 14

Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:

\({\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}\)

Согласно закону Ома:

\(U=I\cdot R\)

Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:

\({\displaystyle P=I(t)^{2}\cdot R,}\)

Формула мощности с учетом напряжения принимает следующий вид:

\({\displaystyle P={{U(t)^{2}} \over R}.}\)

Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:

\({\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}\)

Примечание

Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.

В системе СИ:

\({\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}\)

В вакуумной среде и микрополях:

\({\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}\)

где E — напряженность электрического поля;

B — магнитная индукция;

D — электрическая индукция;

H — напряженность магнитного поля;

с — скорость света;

\(\varepsilon _{0} \)— электрическая постоянная;

\(\mu _{0}\) — магнитная постоянная.

В системе СГС:

\({\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}\)

Формула 15

Энергия электромагнитного поля в колебательном контуре:

\({\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}\)

где U — электрическое напряжение в цепи;

C — электроемкость конденсатора;

I — сила тока;

L — индуктивность катушки или витка с током.

В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).

Формула 16

В системе СИ вектор Пойнтинга определяют, как:

\({\mathbf S}={\mathbf E}\times {\mathbf H}\)

В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.

С другой стороны, формулу для плотности потока энергии можно адаптировать для случая стационарных электрических и магнитных полей:

\({\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H}.}\)

Как измерить ЭМП

Вектором магнитной индукции B характеризуется интенсивность силового действия со стороны магнитного поля (на полюс или на ток), и поэтому является его главной характеристикой в данной точке пространства.

Значит, исследуемое магнитное поле может взаимодействовать силовым образом либо с магнитом, либо с элементом тока. Кроме того, оно способно наводить ЭДС индукции в контуре, если магнитное поле, пронизывающее контур, изменяется с течением времени, либо если контур изменяет свое положение относительно магнитного поля.

На элемент проводника с током длиной dl в магнитном поле с индукцией B будет действовать сила F, величина которой может быть найдена с помощью следующей формулы:

Значит, индукция B исследуемого магнитного поля может быть найдена по силе F, действующей на помещенный в это магнитное поле проводник заданной длины l с постоянным током известной величины I.

Магнитные измерения удобно проводить практически, используя величину, называемую магнитным моментом. Магнитный момент Pm характеризует контур площади S с током I, а величина магнитного момента определяется так:

ρm= I×S

Если используется катушка из N витков, то ее магнитный момент будет равен: 

ρm= I×N×S

Механический момент взаимодействия магнитных сил M можно найти, исходя из значений магнитного момента Pm и индукции магнитного поля B следующим образом:

Однако для измерения магнитного поля не всегда удобно пользоваться его механическими силовыми проявлениями. Есть еще одно явление, на которое можно опереться. Это явление электромагнитной индукции. Закон электромагнитной индукции в математической форме записывается формулой:

Итак, магнитное поле проявляет себя силами либо наводимой ЭДС. При этом источником самого магнитного поля является электрический ток.

Если ток, порождающий магнитное поле в данной точке пространства известен, то напряженность магнитного поля в этой точке (на расстоянии r от элемента тока) можно найти с помощью закона Био-Савара-Лапласа:

Стоит отметить, что магнитная индукция B в вакууме связана с напряженностью магнитного поля H (порожденного соответствующим током) следующим соотношением: Β0=μ0H. 

Магнитная постоянная вакуума в системе СИ определяется через ампер. Для произвольной же среды данная константа есть отношение магнитной индукции в данной среде к магнитной индукции в вакууме, и называется магнитной проницаемостью среды: μ=B/B0. 

Магнитная проницаемость воздуха практически совпадает с магнитной проницаемостью вакуума, поэтому для воздуха магнитная индукция B практически тождественна напряженности магнитного поля H.

Единица измерения магнитной индукции в системе СИ — тесла , в системе СГС — Гаусс , причем 1 Тл = 10000 Гс. Измерительные приборы для определения индукции магнитного поля, называются тесламетрами. 

Напряженность H магнитного поля измеряется в амперах на метр (А/м), причем 1 ампер/метр задается как напряженность магнитного поля соленоида бесконечной длины с единичной плотностью витков при протекании по данному соленоиду тока в 1 ампер. Один ампер на метр можно определить и иначе: это напряженность магнитного поля в центре круглого витка с током в 1 ампер при диаметре витка в 1 метр.

Стоит отметить такую величину, как магнитный поток индукции — Ф. Это скалярная величина, в системе СИ она измеряется в веберах, а в системе СГС — в максвеллах, причем 1 мкс = 0,00000001 Вб. 1 Вебер — это магнитный поток такой величины, что при убывании его до нуля, по сцепленной с ним проводящей цепи сопротивлением 1 Ом, пройдет заряд в 1 Кулон.

Если принять за исходную величину магнитный поток Ф, то индукция магнитного поля B будет плотностью магнитного потока. Приборы для измерения магнитного потока называются веберметрами. 

Магнитная индукция может определяться либо через силу (или через механический момент), либо через наводимую в контуре ЭДС. Это так называемые прямые измерительные преобразования, при которых магнитный поток или магнитная индукция выражаются через другую физическую величину (силу, заряд, момент, разность потенциалов), однозначно связанную с магнитной величиной посредством фундаментального физического закона.

Преобразования, в которых магнитная индукция B или магнитный поток Ф находятся через ток I, длину l или радиус r, называются обратными преобразованиями. Такие преобразования выполняются с опорой на закон Био-Савара-Лапласа, с использованием известного соотношения между магнитной индукцией B и напряженностью магнитного поля H.

3.10. Работа по перемещению проводника с током в магнитном поле

Длина проводника l, и перемещается он слева направо. Тогда работа по перемещению элемента проводника с током на расстояние dr равна:

.

Условия перемещения:

1. магнитное поле и проводник в пространстве взаимно перпендикулярны, .
2. Направление перемещения проводника параллельно силе, вдоль которой мы совершаем работу по перемещению. То есть

3. — площадочка, заметаемая элементом проводника с током dl при его перемещении на dr. Тогда поток векторов B, проходящих через эту площадку:

Работа по перемещению проводника с током в магнитном поле определяется величиной тока, величиной магнитной индукции и площадью закрываемой (заметаемой) проводником при движении. Она также определяется величиной тока и магнитным потоком, проходящим через площадь, закрываемую проводником при движении.

3.17. Энергия магнитного поля

Как любое поле, магнитное поле обладает энергией. Легче всего исследуется однородное магнитное поле, которое находится в соленоиде.

При замкнутом ключе внутри соленоида накапливается магнитная энергия. Если величину тока не менять в стационарных условиях, то часть тока идет через нагрузку, например, лампочку Л, другая часть через соленоид L.

При выключении ЭДС батареи в момент времени ток, протекающий в соленоиде, уменьшается и вызывает ЭДС электромагнитной индукции, препятствующую этому уменьшению. Эта ЭДС стремиться поддержать ток на нагрузке.

Поэтому величина тока на приборе плавно уменьшиться. Это происходит за счет энергии магнитного поля, накопленной в соленоиде.

Можно записать работу по переносу заряда для поддержания тока в цепи при выключении ключа, которая происходит за счет энергии магнитного поля, запасенной в соленоиде.

а так, как (Закон Фарадея-Ленца) и dq=Idt,

то — закон сохранения энергии.

Тогда полная энергия магнитного поля:

— полная магнитная энергия, запасенная в соленоиде с индуктивностью L. Аналогична ситуация с включением.

Схема включения цепи с соленоидом. Время релаксации τ — время, необходимое для установления в рабочих цепях режима равновесной (стационарной) работы.

3.13. Явление электромагнитной индукции. ЭДС электромагнитной индукции

Проводник, по которому не пропускают ток, помещаем в магнитное поле. Будем перемещать проводник перпендикулярно вектору магнитного поля. По закону Лоренца так как . Мы получили, что свободные заряды, которые, по определению, имеются в проводнике, будут перемещаться вдоль проводника. В результате перераспределения зарядов в проводнике при их движении на концах проводника возникает разность потенциалов, которая создает электрическое поле в проводнике: . Тогда напряженность электрического поля в проводнике

Если подключим гальванометр, то можно выразить напряженность через напряжение . В равновесии Fл=Fк. То есть: . Если закон перемещения проводника в магнитном поле произволен, то разбиваем все перемещение на отрезки dr: , где dS=drℓ — площадь, заметаемая проводником при перемещении. Правило Фарадея: величина разности потенциалов, возникающих на концах проводника при его перемещении в магнитном поле прямо пропорциональна скорости изменения магнитного потока.

Если концы проводника замкнуты между собой, то в цепи протекает ток так, если бы проводник являлся источником тока. Тогда по закону Ампера сила, действующая на проводник с током в магнитном поле (правило левой руки) направлена в сторону, противоположную перемещению проводника в магнитном поле, то есть эта сила препятствует перемещению. Тогда:

1. разность потенциалов, возникающих на концах проводника, называют ЭДС магнитной индукции.
2. поскольку ЭДС вызывает силы, препятствующие движению проводника, то в законе Фарадея ставят знак “минус” (правило Ленца):

3.23. Анализ массово-зарядового состояния (q/m) элементарных частиц

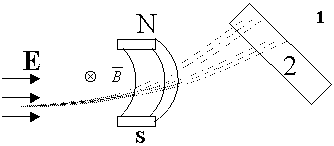
С поверхности вещества испаряют часть атомов или молекул. Как правило, при этом такие атомы обладают зарядовыми свойствами. Далее эти атомы ускоряются в электрическом поле E, и движущийся поток атомов пропускают через магнитное поле B. По закону Лоренца эти заряды в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах оседают атомы разных зарядов. По степени отклонения атомов от прямолинейного распространения можно судить о заряде атома.

Частицы в магнитном поле отклоняются. Тогда на экране за магнитным полем в разных местах, например:

Заряд q= 1e – в точке 2 на экране.

Заряд q=2e – в точке 1 на экране.

Процесс разделения частиц по зарядам называется сепарированием, а прибор, анализирующий состав этих пучков — масспектрограф.

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

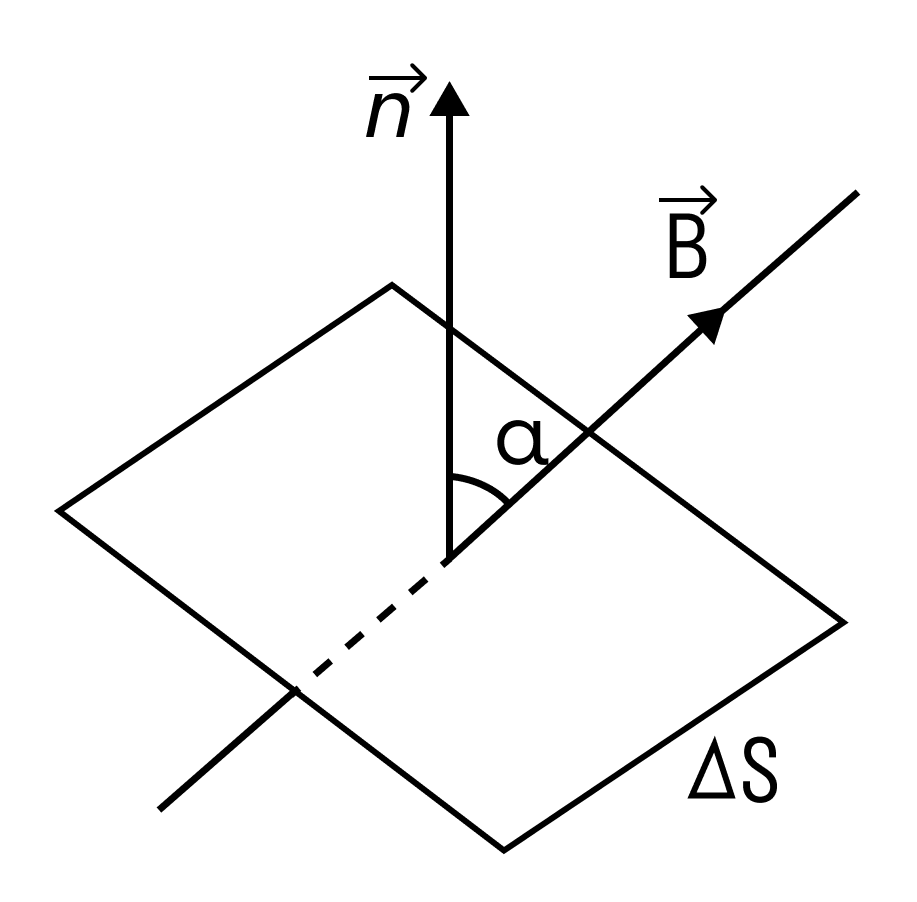
Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​B​, площади поверхности ​S​, пронизываемой данным потоком, и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток Ф — магнитный поток B — магнитная индукция S — площадь пронизываемой поверхности n — вектор нормали (перпендикуляр к поверхности)

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​\( \varepsilon_{is} \)​, возникающая в катушке с индуктивностью ​\( L \)​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея Ɛi — ЭДС индукции ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков Ɛi — ЭДС индукции ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Закон Ома для проводящего контура Ɛi — ЭДС индукции I — сила индукционного тока R — сопротивление контура

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника Ɛi — ЭДС индукции B — магнитная индукция v — скорость проводника [м/с] l — длина проводника

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
• вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

3.14. Явление электромагнитной индукции (взаимоиндукции)

В 1831 году Фарадей установил, что если изменять магнитный поток, проходящий через контур, то в этом контуре возникает ЭДС, препятствующая изменению внешнего магнитного поля. Пусть есть контур I, к которому подключен гальванометр, и контур II, к которому подключен резистор, и источник ЭДС.

1. силовые линии II проводника пересекают первый контур. Если менять величину тока во II контуре, то меняется B2 , то есть магнитный поток, создаваемый вторым контуром также меняется. И по закону Фарадея в первом контуре возникает ЭДС.
2. Удаление или приближение второго контура также вызывает ЭДС в первом.
3. Можно поворачивать контура относительно друг друга, чтобы вызвать ЭДС в I контуре.
4. Вызвать ЭДС можно также изменением магнитной среды, которая находится между контурами.

Приложение:

1. Контуры с током, близко расположенные друг с другом называют связанными.
2. Влияние одного контура на другой возможно только, если ток в контурах переменный (принцип трансформатора). Для усиления взаимодействия используют последовательно соединенные контура – соленоиды.

Пусть:

Соленоид 1 содержит N витков, а соленоид, II: N₂ витков. S — поперечное сечение соленоида.

Если в соленоиде I изменить величину тока, то в соленоиде II возникает ЭДС, равная:

Если в каждом из контуров соленоида возникает ЭДС, то результирующая ЭДС соленоида будет равна произведению числа витков соленоида на ЭДС одного витка: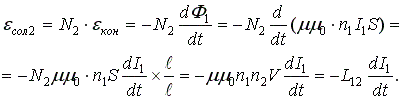

то есть: , где L₁₂ — коэффициент взаимной индукции первого соленоида относительно второго.

Если источник неэлектрических сил подключить ко второму соленоиду, а гальванометр к первому, то ЭДС, возникающую в первом соленоиде можно будет рассчитать аналогично:

, где — коэффициент взаимоиндукции II-ого соленоида относительно первого. Таким образом L₂₁=L₁₂

Энергия соленоида с током формула

Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.

Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции

Проявление явления самоиндукции

При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результате Л1 загорается позже, чем Л2.

При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает.

в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).

От чего зависит ЭДС самоиндукции?

Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике (B

I), следовательно магнитный поток пропорционален силе тока (Ф

I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА

Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.

Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

3.20. Магнетики. Вещества в магнитном поле

Вещества, способные намагничиваться и влиять на направление вектора магнитной индукции внешнего поля B, называются магнетиками.

Способность намагничиваться — создание собственного магнитного поля в веществе, которое или усиливает, или уменьшает внешнее магнитное поле.

Собственные магнитные свойства вещества определяются электронами, связанными с атомами. Строение атома подразумевает наличие электрона e, вращающегося вокруг ядра. Магнитный момент электрона , то есть каждая орбита электрона в атоме обладает собственным магнитным моментом и создает собственное магнитное поле. В целом в веществе суммарные магнитные моменты электронов в атоме расположены хаотично и их сумма зачастую равна нулю.

Под действием внешнего магнитного поля собственные магнитные поля, созданные электронами, упорядочиваются. Это и есть явление намагниченности. Оно может сохраняться после снятия магнитного поля, а может и исчезать. У ферромагнетиков оно сохраняется, а у диа и парамагнетиков исчезает.

В результате поле равно: , где каппа — магнитная восприимчивость, которая определяется внешним воздействием, а и — магнитные моменты электронных орбит.

; — магнитная проницаемость.

.

Для разных веществ значение может принимать как положительные, так и отрицательные значения. В большинстве веществ собственные магнитные моменты атомов (молекул) не зависят друг от друга и хаотично расположены в пространстве. Если к такому веществу приложить внешнее поле, то собственный магнитный момент каждого атома стремится, как волчок, выровнять положение оси вращения вдоль силовых линий внешнего поля.

B_вне — индукция внешнего магнитного поля, Pm- собственный магнитный момент атома.

Изменение собственной оси вращения (собственного магнитного момента) относительно вектора магнитной индукции (внешнего поля) называется прецессией.

Собственный механический момент или количество движения Ls (спин)

Механические моменты электронов в атоме могут отличаться только направлением движения по орбите (вдоль и против часовой стрелки).

1. Если внешнее магнитное поле затрачивает энергию на прецессию, то её результирующее магнитное поле ослабляется. Такие вещества называют диа–магнетиками: .
2. В некоторых веществах внешнее магнитное поле не затрачивает энергию на прецессию, а разворачивает весь атом так, чтобы его собственное магнитное поле совпадало с внешним магнитным полем. Эти вещества -парамагнетики. Для них .

Парамагнетики

Стрелками укажем магнитные моменты отдельных атомов.

Ферромагнетики.

Для объяснения ферромагнетизма вводим понятие доменов. Домен — совокупность атомов с одинаковым направлением собственных магнитных полей. Подобные совокупности атомов требуют меньше энергии для образования доменов, т.е. энергетически более выгодны по сравнению с разрозненными атомами. В целом собственное магнитное поле вещества равно нулю. Под действием внешнего магнитного поля домены могут увеличиваться за счет других доменов вплоть до поглощения неориентированных доменов, то есть все пространство вещества заполняется доменами, ориентированными вдоль поля. При снятии внешнего поля обратной переориентации не происходит, так как это энергетически не выгодно. В этом случае магнитная восприимчивость составляет тысячи и десятки тысяч единиц. Оказывается, реакция вещества на воздействие внешнего магнитного поля носит нелинейный характер. Это определяется способностью собственных магнитных моментов переориентироваться во внешнем магнитном поле. Сначала идёт резкое изменение ориентации во внешнем магнитном поле, магнитные моменты ориентируются вдоль силовых линий магнитного поля. Дальнейшее увеличение магнитного поля не изменяет намагниченность, так как все магнитные моменты уже ориентированы вдоль поля. Зависимость результирующего магнитного поля в веществе в целом в зависимости от внешнего поля носит характер гистерезиса.

B₁ — остаточная индукция. H₁ — коэрцетивная сила.

B₁ — в веществе остается собственное магнитное поле без внешнего магнитного поля H₁ = 0, (так создаются постоянные магниты).

H₁ — внешнее поле, необходимое для снятия собственной намагниченности, B₁=0. Эта величина называется коэрцетивная сила.

Анализ петли гистерезиса см. в разделе “Сегнетоэлектрики”. Если коэрцетивная сила велика, то говорят, что ферромагнетик жёсткий, если мала — то мягкий.

3.29. Анализ III и IV уравнений

Из III уравнения Максвелла следует, что в объеме, из которого исходят силовые линии электрического поля, находятся электрические заряды, а из IV следует, что объем, из которого исходят силовые линии магнитного поля не содержит зарядов магнитного поля.

Это доказательство того, что в природе не существует магнитных зарядов, соответственно, нет потенциала магнитного поля.

Итак, рассмотренные 4 уравнения Максвелла считаются основными, но есть еще три дополнительных.

Эти уравнения соединяют свойства электрических и магнитных полей в вакууме и средах.

Первые два уравнения Максвелла получены из поверхностных интегралов, для которых важно задать направление силовых линий, значит, в уравнениях обязательно отмечается векторность полей. (I)

(I).

(II)

А III и IV уравнения – количественные, то есть скалярные уравнения.

или умножив это уравнение на получим (III).

И наконец (IV).

Система уравнений Максвелла отображает единую теорию электромагнитного поля и показывает, что оно есть единое поле, то есть электрического поля не существует без магнитного, а магнитное поле не существует без электрического. Можно ещё сказать, что переменное магнитное поле порождает неоднородное электрическое, а переменное электрическое поле порождает неоднородное магнитное поле.