Закон ампера: определение, что устанавливает, границы применимости, единицы измерения, формула

Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера

Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.

Анализ задачи:

Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.

Решение:

В ходе решения выполним объяснительные рисунки: изобразим проводники А и В, покажем направление тока в них и др.

Определим направление силы Ампера, действующая на проводник А, находящегося в магнитном поле проводника В.

1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (отметка «•»).

2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.

3) Приходим к выводу: проводник А привлекается к проводнику В.

Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.

1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (отметка «х»).

2) Определим направление силы Ампера, действующая на проводник В.

3) Приходим к выводу: проводник В привлекается к проводнику А.

Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.

Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?

Анализ задачи:

Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:

сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх)
значение силы Ампера равна значению силы тяжести FA = Fтяж

Направление тока определим, воспользовавшись правилом левой руки.

Решение:

Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.

Учитываем, что FA = Fтяж. FA= BIlsinα, где sin α = 1; Fтяж = mg

Из последнего выражения найдем силу тока: I = mg/Bl

Проверим единицу, найдем значение искомой величины.

Ответ: I = 8 А; Ток в направлении от нас.

Подводим итоги

Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: FA= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.

Направление силы Ампера

Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются). Сила ($\overrightarrow{F}$), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции ($\overrightarrow{B}$). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует. Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера. Если направление вектора $\overrightarrow{B}$ составляет некоторый угол с направлением тока, то для выяснения направления силы Ампера целесообразно разложить вектор магнитной индукции на две составляющие (рис.1):

где $\overrightarrow{B_{\bot }}$ — перпендикулярна току, $\overrightarrow{B_{II}}$ — параллельна току. Только $\overrightarrow{B_{\bot }}$ — вызывает действие поля, к ней надо применять правило левой руки.

Рис. 1

Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.

Применение в жизни

В электротехнике закон Ампера «играет» одну из самых важных «ролей». Давайте обсудим случаи его применения на практике. Электропривод — это основа практически каждого предприятия. Для передвижения или доведения до действий всевозможных систем, таких как:

электромобили;
трамваи;
троллейбусы;
автоматизированные задвижки трубопроводов;
грузоподъемных механизмов;
электротранспорта (электровозы на ЖД) и других,

применяются двигатели и электромагнитные исполнительные механизмы.

В результате содействия между обмотками ротора и статора, сила вынуждает двигатель вращаться.

Чтобы заставить обмотки вращаться, их либо переключают с помощью щеточного узла и коллектора в двигателях постоянного тока, либо используют переменный ток.

Ее действие просматривается при коротких замыканиях на линиях электропередач. Там, под влиянием сверхбольших токов, провода и шины начинают изгибаться.

В рельсотроне в момент выстрела раздвигаются рельсы. Это предопределено уже вышеперечисленными причинами.

Общее представление об электромагнитном поле

Длительное время представления об электрическом и магнитном поле не связывались между собой. Практические эксперименты подтверждали, что каждое из них имеет свои особенные свойства. Исследования Фарадея и Максвелла показали, что существует электромагнитное поле, которое может проявлять себя как электрическое или магнитное. Его можно описать с мощью вектора напряжённости. Если знать величину и направление данного вектора, то можно рассчитать силу воздействия.

Первым из учёных, кто обратил внимание на взаимное влияние магнитного поля и тока был известный учёный Х. К

Эрстед. Он исследовал влияние проводника с текущим по нему током на положение стрелки компаса. После этого учёные стали систематически изучать различные варианты взаимодействия.

Ампер появился на свет в 1775 году в Лионе. С детства он проявлял страсть к математике. Будучи подростком, изучал труды Эйлера и Лагранжа. Профессором математики Ампер стал в 1809 году, а в 1814 году был избран в академию наук. Хотя он преимущественно занимался математикой, его интересовала физика и некоторые другие науки.

Ампер был не первым человеком, который проявил интерес к связи магнитных и электрических полей, однако он впервые постарался найти точное математическое описание происходящих процессов. Им был не только установлен факт взаимодействия между электрическими токами, но и сформулирован закон данного явления.

Ампер доказал, что проводники начинают взаимодействовать, если по каждому из них протекает ток. В этом случае между ними возникают силы отталкивания или притягивания. В 1826 году Ампер впервые опубликовал результаты своего исследования, с помощью которого он изучал взаимодействие параллельных токов.

Основываясь на экспериментах, учёный сделал предположение, которое впоследствии получило название «гипотеза Ампера». Понимая, как влияет ток на магнитное поле, он сумел доказать, что вещество состоит из совокупности чрезвычайно маленьких круговых токов. Каждый из них порождает очень слабое магнитное поле. Поскольку все эти токи ориентированы хаотично, то внешне магнитное поле практически не проявляется. Однако в магнитах все круговые токи одинаково направлены и их воздействие складывается. Этим объясняются их особые свойства и практическое использование.

Ампер, используя свой закон, также объяснил эффект намагничивания. Согласно ему, у некоторых веществ под воздействием магнитного поля происходит упорядочивание круговых токов, и они постепенно ориентируются в одну сторону.

Эта гипотеза стала одним из источников теории магнетизма. Она смогла объяснить явление только частично, так как не дала ответа на вопрос о том, почему некоторые вещества подвергаются воздействию внешнего магнитного поля незначительно. Также остался необъяснённым вопрос, почему при намагничивании одни вещества создают магнитный поток сонаправленный внешнему полю (парамагнетики), а другие — противоположно направленный (диамагнетики).

Закон Ампера

Элементарная сила Ампера определена законом (или формулой) Ампера:

где I – сила тока, – малый элемент длины проводника – это вектор, равный по модулю длине проводника, направленный в таком же направлении как вектор плотности тока, – индукция магнитного поля, в которое помещен проводник с током.

Иначе эту формулу для силы Ампера записывают как:

где – вектор плотности тока, dV – элемент объема проводника.

Модуль силы Ампера находят в соответствии с выражением:

где – угол между векторами магнитной индукции и направление течения тока. Из выражения (3) очевидно, что сила Ампера максимальна в случае перпендикулярности линий магнитной индукции поля по отношению к проводнику с током.

Великий учёный

Имя André-Marie Ampère увековечено среди имён других 72 учёных на первом этаже Эйфелевой башни. Его вклад в науку заложил фундамент для понимания явлений электромагнетизма. Хоть Андре-Мари был не первым человеком, обнаружившим связь между электричеством и магнетизмом, он впервые попытался теоретически объяснить и продемонстрировать, как в математических выражениях расписывается связь между этими явлениями. Ампер с помощью устройства собственного изобретения смог измерить ток, а не просто зафиксировать его присутствие.

Учёный родился в Лионе в 1775 году и был современником Французской революции. Будучи сыном коммерсанта и чиновника, он с ранних лет проявлял страсть к математике, а став подростком, читал сложные трактаты Эйлера и Лагранжа. Получил должность профессора математики Парижской политехнической школы в 1809 году, а в 1814 г. был избран членом Академии наук. Хоть Андре-Мари преподавал математику, его интересы распространялись на многие области, в том числе на химию и физику.

Наиболее значимый документ Ампера по теории электричества был опубликован в 1826 году. Теоретические основы, представленные в этом труде, стали фундаментом для дальнейших открытий в области электричества и магнетизма. Получив известность и признание в высокоуважаемых академиях и научных организациях мира, Ампер избегал публичности и чувствовал себя счастливым только в скромной лаборатории в Париже.

Несмотря на достижения и место в обществе, судьба учёного сложилась довольна трагично. В 1793 году его отца гильотинировали за политические убеждения. Это событие стало причиной глубокой депрессии Андре-Мари и едва не свело его с ума. Первая жена рано ушла из жизни после продолжительной болезни, второй брак был неудачным и несчастливым. Сам Ампер умер в 1836 году от воспаления лёгких в Марселе и был похоронен на кладбище Монмартр в Париже.

Направление (устремление) силы Ампера

Для определения направления прибегают к правилу левой руки. Для этого Вам потребуется разместить раскрытую ладонь левой руки возле проводника таким образом, чтобы в нее входили векторы индукции магнитного поля, а четыре открытых пальца показывали направление движение тока.

Вследствие этого, большой палец укажет, куда устремлены силы Ампера и Лоренца.

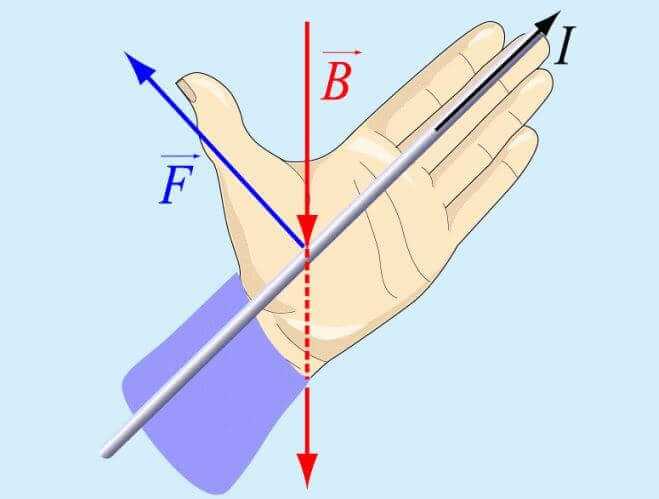
Давайте вспомним, как найти направление вектора магнитной индукции… Он находится путем применения правила правой руки: четырьмя пальцами правой руки «обнять» проводник, а большой палец выпрямить под углом 90 градусов таким образом, чтоб он показывал направление тока.

Вследствие этого, четыре согнутых пальца будут изображать круги вокруг токопроводящей нити и указывать, как пробегают линии магнитного поля.

Закон Ампера

Также законом Ампера называют закон, который определяет силу действия магнитного поля не небольшую часть проводника, по которой протекает ток. В данном случае она определяется как результат умножения плотности тока, который идёт по проводнику, на индукцию магнитного поля, в котором проводник находится.

Из самого закона Ампера сделаны выводы, что сила Ампера равняется нулю, если величина угла, расположенного между током и линией магнитной индукции, тоже будет равняться нулю. Другими словами, проводник для достижения нулевого значения должен быть расположен вдоль линии магнитной индукции.

Закон Ампера – определение

Андре Ампер в 1920 году дал определение тому, с какой силой магнитное поле влияет на проводник, помещённый в него. Он установил прямое соотношение между силой, возникающей вокруг проводника, силой тока, модулем магнитной индукции и синусом угла между вектором магнитной индукции и направлением тока.

Выражение имеет вид:

FА = B *I*L*sinα,

где:

FА – сила Ампера, Н;
В – модуль магнитной индукции;
I – сила тока, А;
L – длина отрезка проводника, м.

Определение справедливо для проводника, по которому происходит постоянно направленное движение электронов.

Что такое сила Ампера

Собственно сила ампера и является той силой действия магнитного поля на проводник, по которому идет ток. Сила Ампера вычисляется по формуле как результат умножения плотности тока, идущего по проводнику на индукцию магнитного поля, в котором находится проводник. Как результат формула силы Ампера будет выглядеть так

са=ст*дчп*ми

Где, са – сила Ампера, ст – сила тока, дчп – длина части проводника, ми – магнитная индукция.

Сила Ампера, Закон Ампера, правило левой руки:

Сила Ампера: это сила, действующая на проводник с током, помещенный в магнитное поле
Правило левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению движения тока, то отогретый на 90о большой палец покажет направление силы, действующей на отрезок проводника

Сила взаимодействия параллельных токов. Закон Ампера

Если взять два проводника с электрическими токами, то они будут притягиваться друг к другу, если токи в них направлены одинаково и отталкиваться, если токи текут в противоположных направлениях. Сила взаимодействия, которая приходится на единицу длины проводника, если они параллельны, может быть выражена как:

где $I_1{,I}_2$ — токи, которые текут в проводниках, $b$- расстояние между проводниками, $в\ системе\ СИ\ {\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}\ (Генри\ на\ метр)$ магнитная постоянная.

Закон взаимодействия токов был установлен в 1820 г. Ампером. На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную $2\cdot {10}^{-7}Н$ на каждый метр длины.

Как измерить ЭМП

Вектором магнитной индукции B характеризуется интенсивность силового действия со стороны магнитного поля (на полюс или на ток), и поэтому является его главной характеристикой в данной точке пространства.

Значит, исследуемое магнитное поле может взаимодействовать силовым образом либо с магнитом, либо с элементом тока. Кроме того, оно способно наводить ЭДС индукции в контуре, если магнитное поле, пронизывающее контур, изменяется с течением времени, либо если контур изменяет свое положение относительно магнитного поля.

На элемент проводника с током длиной dl в магнитном поле с индукцией B будет действовать сила F, величина которой может быть найдена с помощью следующей формулы:

Значит, индукция B исследуемого магнитного поля может быть найдена по силе F, действующей на помещенный в это магнитное поле проводник заданной длины l с постоянным током известной величины I.

Магнитные измерения удобно проводить практически, используя величину, называемую магнитным моментом. Магнитный момент Pm характеризует контур площади S с током I, а величина магнитного момента определяется так:

ρm= I×S

Если используется катушка из N витков, то ее магнитный момент будет равен:

ρm= I×N×S

Механический момент взаимодействия магнитных сил M можно найти, исходя из значений магнитного момента Pm и индукции магнитного поля B следующим образом:

Однако для измерения магнитного поля не всегда удобно пользоваться его механическими силовыми проявлениями. Есть еще одно явление, на которое можно опереться. Это явление электромагнитной индукции. Закон электромагнитной индукции в математической форме записывается формулой:

Итак, магнитное поле проявляет себя силами либо наводимой ЭДС. При этом источником самого магнитного поля является электрический ток.

Если ток, порождающий магнитное поле в данной точке пространства известен, то напряженность магнитного поля в этой точке (на расстоянии r от элемента тока) можно найти с помощью закона Био-Савара-Лапласа:

Стоит отметить, что магнитная индукция B в вакууме связана с напряженностью магнитного поля H (порожденного соответствующим током) следующим соотношением: Β0=μ0H.

Магнитная постоянная вакуума в системе СИ определяется через ампер. Для произвольной же среды данная константа есть отношение магнитной индукции в данной среде к магнитной индукции в вакууме, и называется магнитной проницаемостью среды: μ=B/B0.

Магнитная проницаемость воздуха практически совпадает с магнитной проницаемостью вакуума, поэтому для воздуха магнитная индукция B практически тождественна напряженности магнитного поля H.

Единица измерения магнитной индукции в системе СИ — тесла , в системе СГС — Гаусс , причем 1 Тл = 10000 Гс. Измерительные приборы для определения индукции магнитного поля, называются тесламетрами.

Напряженность H магнитного поля измеряется в амперах на метр (А/м), причем 1 ампер/метр задается как напряженность магнитного поля соленоида бесконечной длины с единичной плотностью витков при протекании по данному соленоиду тока в 1 ампер. Один ампер на метр можно определить и иначе: это напряженность магнитного поля в центре круглого витка с током в 1 ампер при диаметре витка в 1 метр.

Стоит отметить такую величину, как магнитный поток индукции — Ф. Это скалярная величина, в системе СИ она измеряется в веберах, а в системе СГС — в максвеллах, причем 1 мкс = 0,00000001 Вб. 1 Вебер — это магнитный поток такой величины, что при убывании его до нуля, по сцепленной с ним проводящей цепи сопротивлением 1 Ом, пройдет заряд в 1 Кулон.

Если принять за исходную величину магнитный поток Ф, то индукция магнитного поля B будет плотностью магнитного потока. Приборы для измерения магнитного потока называются веберметрами.

Магнитная индукция может определяться либо через силу (или через механический момент), либо через наводимую в контуре ЭДС. Это так называемые прямые измерительные преобразования, при которых магнитный поток или магнитная индукция выражаются через другую физическую величину (силу, заряд, момент, разность потенциалов), однозначно связанную с магнитной величиной посредством фундаментального физического закона.

Преобразования, в которых магнитная индукция B или магнитный поток Ф находятся через ток I, длину l или радиус r, называются обратными преобразованиями. Такие преобразования выполняются с опорой на закон Био-Савара-Лапласа, с использованием известного соотношения между магнитной индукцией B и напряженностью магнитного поля H.

Направление (устремление) силы Ампера

Вследствие этого, большой палец укажет, куда устремлены силы Ампера и Лоренца.

Направление силы Ампера

Сила является векторной величиной, направление которой можно определить. Предположим, что проводник с током находится между двумя магнитными полюсами и расположен под прямым углом к линиям магнитной индукции. Согласно закону Ампера, на проводник действует сила, которая равна:

F = B*L*I

Направление вектора данной силы можно определить с помощью векторного произведения:

В том случае, когда полюса магнита находятся в неподвижном состоянии, то есть статичны, векторное произведение определяется только параметрами электричества, в частности, его направлением. Выяснить, как направлена сила Ампера, можно с помощью известного правила левой руки.

Определение

Правило левой руки: если ладонь расположить навстречу магнитным линиям, а пальцы – вдоль проводника, в сторону устремления тока, то на ориентацию силы Ампера укажет большой палец, образующий прямой угол с ладонью.

Если представить, что направление электрического тока изменилось, то направление вектора силы Ампера поменяет направление на противоположное. Модуль вектора зависит прямо пропорционально от всех сомножителей. Однако на практике данная величина регулируется путем изменения параметров в электрической цепи, к примеру, с целью регулировки мощности электрического двигателя.

Направление силы Ампера

Принимая к сведению то, что сила – векторная величина, определим её направление. Рассмотрим случай, когда проводник с током расположен между двумя полюсами магнитов под прямым углом к линиям магнитной индукции.

Выше мы установили, что согласно закону Ампера, действующая на данный проводник сила, равна: F = B*L*I. Направление вектора рассматриваемой силы определяется по результатам векторного произведения:

Если полюса магнита статичны (неподвижны), то векторное произведение будет зависеть только от параметров электричества, в частности, от того, в какую сторону оно течёт.

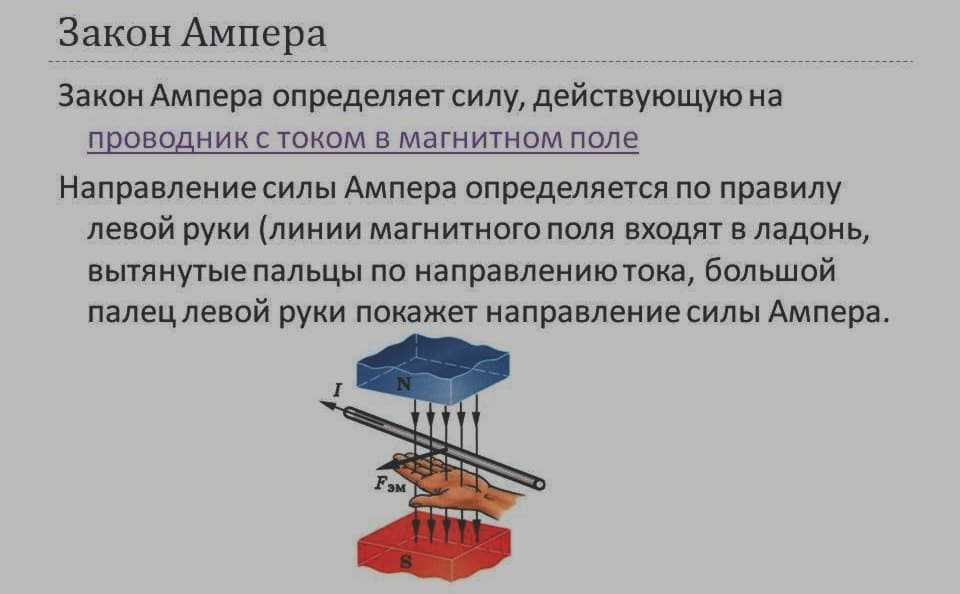Рис. 4. Интерпретация правила

Измените мысленно направление электрического тока, и вы увидите, что направление вектора Амперовой силы изменится на противоположное. Модуль вектора имеет прямо пропорциональную зависимость от всех сомножителей, но на практике эту величину удобно регулировать путём изменения параметров в электрической цепи (например, для регулировки мощности электродвигателя).

Правило левой руки

Формулировка правила левой руки для силы ампера звучит так:

Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения тока в проводнике, а перпендикулярная составляющая индукции $B_{perp}$ входила в ладонь, то отставленный большой палец покажет направление силы Ампера.

Как пользоваться этим правилом? Разберем примеры.

Допустим, проводник расположен горизонтально, и ток по нему идет вперед. Следовательно, четыре пальца левой руки надо вытянуть вперед по этому направлению.
Теперь допустим, что линии магнитного поля направлены сверху вниз (сверху «север» подковообразного магнита, снизу — «юг»). Следовательно, левую руку надо повернуть ладонью вверх, чтобы линии магнитного поля входили в ладонь и «прокалывали» ее (четыре пальца по-прежнему должны быть вытянуты вперед).
Отставленный большой палец левой руки будет направлен влево. Это и есть направление силы Ампера для данной ситуации.

Другой пример.

Пусть проводник расположен вертикально. А магнитное поле направлено справа налево (справа «север» магнита, слева — «юг»).
Располагаем левую руку четырьмя пальцами вверх. Ладонь открытой стороной должна «смотреть вправо», чтобы магнитные линии входили и «прокалывали» ее.
Отставленный большой палец покажет назад. Именно так и будет направлена сила Ампера в данном случае.

Обратите внимание, что силу Ампера порождает только перпендикулярная составляющая магнитного поля. А значит, руку надо располагать так, чтобы линии магнитного поля всегда входили в нее под углом, максимально близким к прямому

Особым случаем является ситуация, когда направление тока и магнитной индукции совпадает. В этом случае руку невозможно расположить так, чтобы линии магнитной индукции входили в нее. Следовательно, силы Ампера здесь не возникнет. В самом деле, если линии магнитной индукции параллельны направлению тока, то перпендикулярная составляющая этих линий равна нулю, и значение силы Ампера в вышеприведенной формуле также равно нулю.

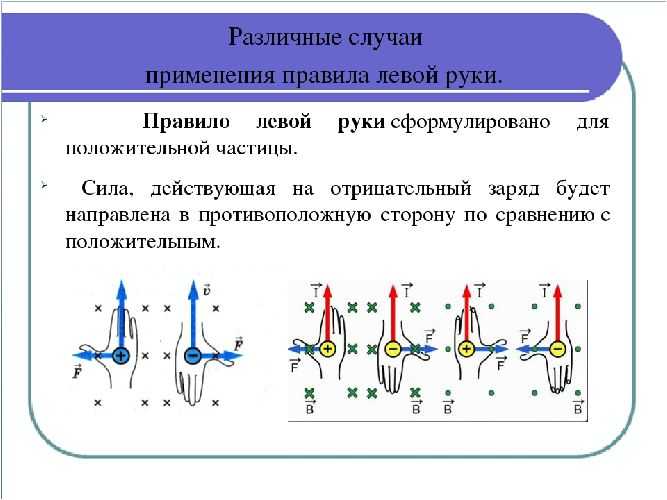
Рис. 3. Различные случаи применения правила левой руки.

Плотность энергии электрического и магнитного полей

Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.

В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.

Формула 12

Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:

${\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}$

где $U=\int E\,dx$ — разность потенциалов, или напряжение.

Формула 13

Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:

${\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}$

где $I(t)={dQ \over dt}$ — сила тока.

Формула 14

Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:

${\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}$

Согласно закону Ома:

$U=I\cdot R$

Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:

${\displaystyle P=I(t)^{2}\cdot R,}$

Формула мощности с учетом напряжения принимает следующий вид:

${\displaystyle P={{U(t)^{2}} \over R}.}$

Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:

${\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}$

Примечание

Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.

В системе СИ:

${\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}$

В вакуумной среде и микрополях:

${\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}$

где E — напряженность электрического поля;

B — магнитная индукция;

D — электрическая индукция;

H — напряженность магнитного поля;

с — скорость света;

$\varepsilon _{0} $— электрическая постоянная;

$\mu _{0}$ — магнитная постоянная.

В системе СГС:

${\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}$

Формула 15

Энергия электромагнитного поля в колебательном контуре:

${\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}$

где U — электрическое напряжение в цепи;

C — электроемкость конденсатора;

I — сила тока;

L — индуктивность катушки или витка с током.

В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).

Формула 16

В системе СИ вектор Пойнтинга определяют, как:

${\mathbf S}={\mathbf E}\times {\mathbf H}$

В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.