Связь энергии магнитного поля и его основных характеристик
На примере длинного соленоида можно рассмотреть проявление энергии магнитного поля. Предположим, что поля является однородным и сосредоточено внутри соленоида. В таком случае, для нахождения силы тока можно воспользоваться формулой:
\(I=\frac{Hl}{N}\)
Здесь H — напряженность магнитного поля соленоида; l — длина соленоида; N — число витков соленоида.
В случае эксперимента с соленоидом:
\(L=\mu \mu _{0}n^{2}Sl\)
Здесь \(\mu\) — магнитная проницаемость сердечника соленоида; S — площадь сечения соленоида; n=Nl.
Таким образом:
\(E_{m}=\frac{\mu \mu _{0}N^{2}Sl}{2l^{2}}\frac{H^{2}l^{2}}{N^{2}}=\mu \mu _{0}\frac{H^{2}}{2}Sl=\mu \mu _{0}\frac{H^{2}}{2}V\)
Как правило, роль энергетической характеристики магнитного поля играет такой параметр, как плотность энергии магнитного поля:
\(\omega =\frac{E_{m}}{V}=\mu \mu _{0}\frac{H^{2}}{2}\)
Данное выражение справедливо в случае любого магнитного поля, несмотря на характер его происхождения. Формула определяет энергию магнитного поля в единице его объема. Если имеется магнитоизотропная среда, то уравнение можно преобразовать, таким образом:
\(\vec{B}=\mu \mu _{0}\vec{H}\)
Следовательно:
\(\omega =\frac{BH}{2}\)
В случае неоднородного магнитного поля целесообразно разбить его на элементарные объемы (dV), то есть малые объемы, в которых магнитное поле считается однородным. Энергия магнитного поля, заключенная в рассматриваемых объемах, составляет:
\(dE_{m}=\omega dV\)
При этом суммарная энергия магнитного поля равна:
\(E_{m}=\int_{V}^{}{\omega dV}\)
Интегрированию в данном случае подлежит весь объем, занимаемый магнитным полем.
От чего зависит величина
Существует ряд некоторых ограничений в применении формулы для расчета энергии магнитного поля. При записи выражения выполнялось несколько условий:
- индуктивность контура, а также магнитная проницаемость вещества стабильны;
- вся энергия источника тока трансформируется в энергию магнитного поля.
Перечисленные условия справедливы лишь в случае вакуума, то есть при \(\mu\)=1
Если контур с током поместить в вещество, то необходимо принимать во внимание следующие параметры:
- намагничивание вещества, что способствует его нагреву;
- объем и плотность вещества в магнитном поле могут изменяться даже при стабильной температуре.
Таким образом, магнитная проницаемость вещества \(\mu\), изменяющаяся при перепадах температуры и плотности среды, не может оставаться постоянной в процессе намагничивания. Также работа источника ЭДС не полностью трансформируется в энергию магнитного поля. В том случае, когда объем вещества изменяется в малой степени, сохраняется стабильной температура среды, внешняя работа затрачивается на увеличение энергии магнитного поля \(E_{m}\) и на теплоотдачу Q, чтобы поддерживать постоянную температуру.
Работа внешних сил, в нашем случае источника тока, совершаемая над телом при квазистатическом изотермическом процессе, соответствует увеличению свободной энергии тела. Таким образом, формула определяет часть свободной энергии намагниченного вещества, которая обладает связью с магнитным полем:
\(\omega =\frac{E_{m}}{V}=\mu \mu _{0}\frac{H^{2}}{2}\)
При малом количестве теплоты Q, относительно энергии поля \(E_{m}\), справедливо равенство:
\(-E_{m}=A_{i}\)
Согласно условию стабильности магнитной проницаемости вещества, выполняется линейная зависимость:
\(\vec{B}=\mu \mu _{0}\vec{H}\)
Выражение применимо при рассмотрении ситуаций в условиях вакуума для парамагнетиков и диамагнетиков. Но при опытах с ферромагнетиками магнитная индукция и напряженность магнитного поля связаны нелинейно, даже при T=const.
Плотность энергии электрического и магнитного полей
Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.
В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.
Формула 12
Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:
\({\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}\)
где \(U=\int E\,dx\) — разность потенциалов, или напряжение.
Формула 13
Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:
\({\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}\)
где \(I(t)={dQ \over dt}\) — сила тока.
Формула 14
Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:
\({\displaystyle P(t)={\frac {dA}{dt}}=U(t)\cdot I(t),}\)
Согласно закону Ома:
\(U=I\cdot R\)
Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:
\({\displaystyle P=I(t)^{2}\cdot R,}\)
Формула мощности с учетом напряжения принимает следующий вид:
\({\displaystyle P={{U(t)^{2}} \over R}.}\)
Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:
\({\displaystyle A=\int P(t)\,dt=\int I(t)^{2}\cdot R\,dt=\int {{U(t)^{2}} \over R}\,dt.}\)
Примечание
Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.
В системе СИ:
\({\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} }{2}}+{\frac {\mathbf {B} \cdot \mathbf {H} }{2}}.}\)
В вакуумной среде и микрополях:
\({\displaystyle u={\varepsilon _{0}E^{2} \over 2}+{B^{2} \over {2\mu _{0}}}=\varepsilon _{0}{\frac {E^{2}+c^{2}B^{2}}{2}}={\frac {E^{2}/c^{2}+B^{2}}{2\mu _{0}}},}\)
где E — напряженность электрического поля;
B — магнитная индукция;
D — электрическая индукция;
H — напряженность магнитного поля;
с — скорость света;
\(\varepsilon _{0} \)— электрическая постоянная;
\(\mu _{0}\) — магнитная постоянная.
В системе СГС:
\({\displaystyle u={\frac {\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} }{8\pi }}.}\)
Формула 15
Энергия электромагнитного поля в колебательном контуре:
\({\displaystyle W={\frac {CU^{2}}{2}}+{\frac {LI^{2}}{2}},}\)
где U — электрическое напряжение в цепи;
C — электроемкость конденсатора;
I — сила тока;
L — индуктивность катушки или витка с током.
В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).
Формула 16
В системе СИ вектор Пойнтинга определяют, как:
\({\mathbf S}={\mathbf E}\times {\mathbf H}\)
В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.
С другой стороны, формулу для плотности потока энергии можно адаптировать для случая стационарных электрических и магнитных полей:
\({\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H}.}\)
Энергия соленоида с током формула
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны). В результате Л1 загорается позже, чем Л2.
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает.
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике (B
I), следовательно магнитный поток пропорционален силе тока (Ф
I). ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник. Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду. Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии. В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
Формула индуктивного сопротивления катушки
Формула магнитного потока
Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:
XL=2πfL.
Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.
Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать. Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
Советуем изучить Задача и особенности заземления трансформаторов.
В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.
Плотность энергии различных систем
В таблице приведена плотность энергии замкнутых систем, включая дополнительные внешние компоненты, такие как окислители или источники тепла, но исключая энергию покоя системы в конечном состоянии. 1 МДж ≈ 278 Вт·ч.
| Название | Плотность энергии на единицу массы (МДж/кг) | Плотность энергии на единицу массы (Вт⋅ч/кг) | Плотность энергии на единицу объёма (МДж/л) | Практическая эффективность использования % |
|---|---|---|---|---|
| Аннигиляция материя + антиматерия | до 89 875 517 873,681 764 (точно) ≈ 9⋅1010 | 24 965 421 631 578,26(7) ≈ 25⋅1012 | Зависит от вступающих в реакцию частиц, электроны и позитроны аннигилируют полностью, при аннигиляции барионов часть энергии в конечном счёте уносят нейтрино | |
| Слияние ядер водорода | 645 000 000 | 179 310 000 000 | ~1–10⋅1012(в ядре Солнца) | |
| Реакция дейтерий-тритий | 337 000 000 | 93 686 000 000 | ||
| Уран-235, используемый в ядерном оружии | 88 250 000 | 24 533 500 000 | 1 681 000 000 | |
| Природный уран (99,3 % U-238, 0,7 % U-235) в реакторе на быстрых нейтронах | 86 000 000 | 23 908 000 000 | ||
| Тепловая энергия от α-распада плутония-238 | 2 200 000 | 611 600 000 | 43 648 000 | |
| Кинетическая энергия спутника Земли на низкой орбите | 33 | 9 167 | ||
| Дизельное топливо в мощной дизельной электростанции (без учёта массы генератора) | 20,1 | 5 583 | 47 % | |
| Бензин (без учёта массы генератора) | 8,1—10,5 | 2250—2917 | 19—24 % | |
| Супермаховик | 1,8 | 500 | 98% | |
| Генератор на водородном топливном элементе, без учёта массы конструкции | 12 | 3000 | ||
| Серебряно-цинковый аккумулятор | 0,47 | 130,6 | 1,8 | |
| Литий-ионный аккумулятор | 0,46—0,72 | 128—200 | 2 | |
| Ni-MH-аккумулятор формата AA ёмкостью 2000 мА·ч | 0,33 | 92 | 1,24 | |
| Тяговый свинцово-кислотный аккумулятор | 0,17 | 47 | ||
| Пусковой свинцово-кислотный аккумулятор | 0,1368 | 38 | 0,337 | |
| 0,1 | ||||
| Ионистор | 0,03 | 6,17 | 0,032 (MAXWELL K2) | |
| Керамический конденсатор | 0,003 | |||
| Электролитический конденсатор | 0,000 639 | 0,1775 | 0,00083 | |
| Плёночный конденсатор | 0,000 180 | 0,05 | 0,0025 (maxwell CM-3) | |
| Гравитационный аккумулятор (груз 1 кг на высоте 1 м) | 0,000 009 8 | 0,0027 | 0,0001 для свинца | |
| Взведенная | 0,0003 | 0,083 | 0,0006 |
«Действие магнитного поля на проводник с током»
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Сила Ампера зависит от длины проводника с током, силы тока в проводнике, модуля магнитной индукции и расположения проводника относительно линий магнитной индукции: FA = BIlsinа.
Для определения направления силы Ампера применяют правило левой руки. Если левую руку расположить в магнитном поле так, чтобы силовые линии входили в ладонь, а четыре пальца были направлены по току, то отогнутый большой палец укажет направление силы, действующей на проводник.
Магнитное взаимодействие можно наблюдать между двумя параллельными токами (опыт Ампера): два параллельных проводника с током отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают.
Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника l и силе тока I в проводнике. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции В. Соответственно, F = BIl. В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записывается в том случае, если линии магнитной индукции перпендикулярны проводнику с током. Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.
Единица магнитной индукции = 1Н / 1А • 1м = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1Н при силе тока в проводнике 1 А.
Магнитное поле действует также на движущиеся заряженные частицы. При этом сила (сила Лоренца) зависит от модуля магнитной индукции, заряда частицы, а также от модуля и направления её скорости.
Электрический двигатель
Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся, потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ab, противоположна силе, действующей на сторону cd.
Советуем изучить Ряд сопротивления резистора Е24
Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.
В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.
Действие магнитного поля на проводник с током
Конспект урока по физике в 8 классе «Действие магнитного поля на проводник с током».
Следующая тема: «Электромагнитная индукция. Опыты Фарадея».
Вопрос о локализации энергии магнитного поля
Для постоянных магнитных полей, которые создаются неподвижными постоянными токами, непонятно, где локализуется энергия. Возьмем выражение для магнитной энергии соленоида:
$E_{m}=\frac{IѰ}{2}\left( 20 \right)$),
где $Ѱ=BSN$ – потокосцепление, то есть магнитный поток через витки соленоида. В этом энергия поля кажется энергией тока, так как он является носителем.
Однако энергию соленоида можно представить и так:
$E_{m}=\frac{B^{2}}{2\mu \mu_{0}}lS\, \left( 21 \right)$.
где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.
Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.
При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.
Энергия электромагнитного поля: формула, обозначение, в чём измеряется
При проведении опытов с катушкой и лампочкой накаливания в электрической цепи можно заметить интересное явление. После отключения индукции от источника электропитания, подключенная к ней параллельно лампа накаливания даёт кратковременную вспышку. В сети возникает ток благодаря воздействию электродвижущей силы самоиндукции. В качестве источника энергии для явления задействуется магнитное поле соленоида.
Для простоты расчёта предположим, что сила тока в цепи снижается линейно.
ЭДС самоиндукции при этом вычисляется по формуле:
где t – время, за которое ток падает до нуля.
За этот временной интервал в цепи «пробегает» заряд:
Проделанная магнитным полем работа равняется:
Это максимальная энергия магнитного поля катушки, вычисляется по формуле (обозначается Wm или W):
Читается как: сила магнитного поля катушки равняется половине произведения квадрата силы протекающего по ней тока I на индуктивность L.
Для конденсатора вычисляется иначе: , C-ёмкость конденсатора.
Многие не знают, в чем измеряется энергия магнитного поля тока катушки. В системе единиц СИ это джоуль (Дж), названный в честь британского физика.
Уравнение плотности энергии магнитного поля
| Энергия магнитного поля |
|
Рассмотрим случай, о котором мы уже говорили (рис. 5.6). Сначала замкнем соленоид L на источник ЭДС , в нем будет протекать ток . Затем в момент времени переключим ключ в положение 2 – замкнем соленоид на сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа: , или
Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией
Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида: ; отсюда Подставим эти значения в формулу (5.5.3):
Обозначим w – плотность энергии, или энергия в объеме V, тогда
но т.к. , то
Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле
а плотность энергии
Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника: , отсюда . Т.к. в вакууме , имеем 1. Какие опыты Фарадея легли в основу открытия явления электромагнитной индукции? 2. Что является причиной возникновения ЭДС индукции в замкнутом проводящем контуре? От чего и как зависит ЭДС индукции, возникающая в контуре? 3. В чем заключается явление электромагнитной индукции? 4. Почему для обнаружения индукционного тока лучше использовать замкнутый проводник в виде катушки, а не в виде одного витка провода? 5. Сформулируйте правило Ленца, проиллюстрировав его примерами. 6. Как направлен индукционный ток? 7. Всегда ли при изменении магнитной индукции в проводящем контуре в нем возникает ЭДС индукции? индукционный ток? 8. Чему равна ЭДС индукции контура? 9. Сформулируйте закон Ома для контура. 10. Как связано направление индукционного тока и направление скорости изменения потока магнитной индукции? 11. Сформулируйте закон Фарадея для контура с током, состоящего из одного и нескольких витков. 12. Возникает ли индукционный ток в проводящей рамке, поступательно движущейся в однородном магнитном поле? 13. Покажите, что закон Фарадея есть следствие закона сохранения энергии. 14. Какова природа ЭДС электромагнитной индукции? 15. Выведите выражение для ЭДС индукции в плоской рамке, равномерно вращающейся в однородном магнитном поле. За счет чего ее можно увеличить? 16. Что такое вихревые токи? Вредны они или полезны? 17. Почему сердечники трансформаторов не делают сплошными? 18. Какое явление называется скин-эффектом? 19. Произведите классификацию ускорителей. 20. Каковы параметры линейных ускорителей. 21. Когда заряженная частица движется в магнитном поле по спирали? От чего зависит шаг спирали? Ответы подтвердите выводами формул. 22. Что такое ускорители заряженных частиц? Какие они бывают и чем характеризуются? 23. Почему для ускорения электронов не применяются циклотроны? 24. В чем заключается принцип автофазировки? Где он используется? 25. Когда ЭДС самоиндукции больше – при замыкании или размыкании цепи постоянного тока? 26. В чем заключается физический смысл индуктивности контура? взаимной индуктивности двух контуров? От чего они зависят? 27. В чем заключаются явления самоиндукции и взаимной индукции? Вычислите ЭДС индукции для обоих случаев. 28. В чем заключается физический смысл времени релаксации ? Докажите, что имеет размерность времени. 29. Запишите и проанализируйте выражения для объемной плотности энергии электростатического и магнитного полей. Чему равна объемная плотность энергии электромагнитного поля? 30. Напряженность магнитного поля возросла в два раза. Как изменилась объемная плотность энергии магнитного поля? 31. Приведите соотношение между точками в первичной и вторичной обмотках повышающего трансформатора. В таблице 5.1 приведены сравнительные характеристики электрического и магнитного полей. |
Наличие магнитного поля вокруг проводника или катушки с током
При подключении соленоида (катушки) в электрическую цепь вокруг нее формируется поле. Характеристики поля зависят от ряда параметров: от средовых особенностей окружения, токовой силы (она измеряется в амперах) и материала, из которого изготовлен проводник или обмотка катушки. В полевом пространстве могут образовываться электромагнитные волны. Так как на полевой энергетический потенциал, прежде всего, оказывает влияние сила текущего в системе электротока, можно сделать вывод, что работа тока по генерированию магнитного пространства будет эквивалентной энергии последнего. Если в систему подключена катушка с магнитным сердечником, то на энергетическую плотность будет влиять полевая энергия в вакууме и в материале, из которого сделан сердечниковый элемент.
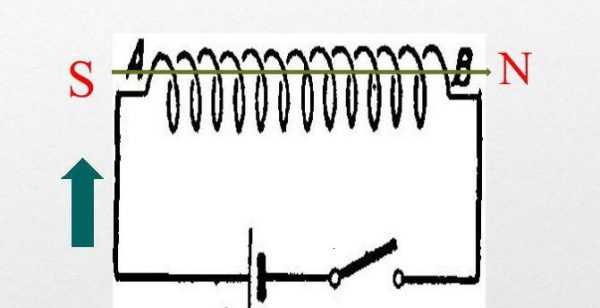Подключение индуктивной катушки к источнику тока
Для изучения динамики явления можно рассмотреть электроцепь, включающую в себя дроссель, лампу, замыкающий ключ и источник постоянного электротока. Когда ключик замыкается, токовый путь будет идти от «положительного» зажима источника через лампу и индуктивную катушку. Поначалу лампа накаливания загорится ярче, что связано со значительной величиной сопротивления дроссели. По мере того, как сопротивление будет падать, а проходящий через обмотку ток увеличиваться, интенсивность горения лампочки будет понижаться. Связано это с тем, что первое время подаваемый на дроссель ток имеет значение, пропорциональное току высокой частоты.
Чтобы практически построить цепь, подходящую для расчета, нужно, чтобы энергетический ресурс источника питания затрачивался на генерирование магнитного поля. Поэтому параметрами внутреннего сопротивления дроссели и питательного источника допустимо пренебрегать.
Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки. Второй закон Кирхгофа. Второй закон Кирхгофа
Второй закон Кирхгофа
Работа электрического поля по перемещению заряда
Понятие работы A{\displaystyle A} электрического поля E{\displaystyle E} по перемещению заряда Q{\displaystyle Q} вводится в полном соответствии с определением механической работы:
- A=∫F(x)dx=∫Q⋅E(x)dx=Q⋅U,{\displaystyle A=\int F(x)\,dx=\int Q\cdot E(x)\,dx=Q\cdot U,}
где U=∫Edx{\displaystyle U=\int E\,dx} — разность потенциалов (также употребляется термин напряжение).
Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t){\displaystyle U(t)}, в таком случае формулу для работы следует переписать следующим образом:
- A=∫U(t)dQ=∫U(t)I(t)dt,{\displaystyle A=\int U(t)\,dQ=\int U(t)I(t)\,dt,}
где I(t)=dQdt{\displaystyle I(t)={dQ \over dt}} — сила тока.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.