Магнитные свойства вещества

Статьи по Теме

• Магнитная постоянная
• Магнитостатический
• Магнитная восприимчивость
• Разрешающая способность
• Нежелание
• Ферромагнетизм

Электромагнетизм
Электростатический	Электрическое поле Электрический заряд Закон Кулона Электрический потенциал Электростатическое давление
Магнитостатический	Магнитное поле Магнитный момент Намагничивание Закон Био и Савара
Электрокинетический	Ампер Электромагнитное поле Ток смещения Электроэнергия вихревые токи Уравнения Ефименко Уравнения Максвелла Электродвижущая сила Сила Лоренца Электромагнитная индукция Закон Ленца-Фарадея Потенциалы Льенара-Вихерта Электромагнитное излучение
Магнетизм	Катушка Магнитная цепь Домен Вайс Переворот магнитного поля Земли Закон Кюри Закон Кюри-Вейсса Магнитная проницаемость Магнитная восприимчивость Магнитное поведение Антиферромагнетизм Диамагнетизм Ферримагнетизм Ферромагнетизм Гелимагнетизм Парамагнетизм Суперпарамагнетизм
Автоматический Электричество Электрохимия Электронный Электротехника Робототехника Обработка сигналов

Комплексная проницаемость, число проницаемости

В частности, в электротехнике векторы полей и, соответственно, комплексная проницаемость используются для регистрации эффектов, зависящих от времени .

μ^знак равноμs′-j⋅μs″.{\ displaystyle {\ hat {\ mu}} = {\ mu _ {\ mathrm {s}}} ‘- \ mathrm {j} \ cdot {\ mu _ {\ mathrm {s}}}’ ‘.}

Реальная часть комплексной проницаемости соответствует нормальной проницаемости. Мнимая часть, с другой стороны, описывает величину потерь на перемагничивание.
μs′{\ displaystyle {\ mu _ {\ mathrm {s}}} ‘}μs″{\ displaystyle {\ mu _ {\ mathrm {s}}} »}

За исключением ферромагнетиков со значительно более высокой относительной проницаемостью, чем один, мнимая часть комплексной проницаемости также незначительна, как и частотная зависимость проницаемости. Результатом является скалярная, не зависящая от частоты проницаемость:

μзнак равноμ⋅μр.{\ displaystyle \ mu = \ mu _ {0} \ cdot \ mu _ {\ mathrm {r}}.}

В случае ферромагнитных материалов частотной зависимостью нельзя пренебрегать для многих технических приложений, это приводит к:

μ^(ж)знак равноμs′(ж)-j⋅μs″(ж){\ displaystyle {\ hat {\ mu}} \, (f) = {\ mu _ {\ mathrm {s}}} ‘\, (f) — \ mathrm {j} \ cdot {\ mu _ {\ mathrm {s}}} » \, (f)}

где — частота переменного магнитного поля. Мнимая часть напрямую связана с движением стенок Блоха в материале, а резонанс дает максимум, обычно в диапазоне 10–1000 кГц.
ж{\ displaystyle f}μs″(ж){\ displaystyle {\ mu _ {\ mathrm {s}}} » (е)}

Как и многие физические свойства материалов, комплексная проницаемость в ее обобщенной линейной форме на самом деле является трехмерным тензором второго порядка. Однако для большинства материалов анизотропия магнитных свойств настолько мала, что достаточно описания скалярной комплексной проницаемости.

литература

• Ганс Фишер: Материалы в электротехнике. Состав, свойства, тестирование, применение. 2-е исправленное издание. Карл Хансер Верлаг, Мюнхен и др., 1982, ISBN 3-446-13553-7 .
• Хорст Кухлинг: Карманный справочник по физике. 4-е издание. Verlag Harri Deutsch, Thun et al.1982 , ISBN 3-87144-097-3 .
• Гюнтер Шпрингер: Опыт в области электротехники. 18-е полностью переработанное и дополненное издание. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 ( Europa- Lehrmittel 30318).
• Хорст Штёкер (Hrsg.): Карманный справочник по физике. Формулы, таблицы, обзоры. 4-е исправленное издание. Verlag Harri Deutsch, Thun et al.2000 , ISBN 3-8171-1628-4 .

Классификация

Числа проницаемости для выбранных материалов

Средняя	µ r	Классификация
Сверхпроводник типа 1	идеально диамагнитный
Свинец , олово	<1 (прибл. 0,999 …)	диамагнитный
медь	0,9999936 = 1 — 6,4 · 10 −6	диамагнитный
водород	1 — 2,061 · 10 −9	диамагнитный
вода	0,999991 = 1 — 9 · 10 −6	диамагнитный
пылесос	1	(нейтральный)
Полиэтилен	~ 1	(нейтральный)
воздуха	примерно 1 + 4 · 10 −7	парамагнитный
алюминий	1 + 2,2 · 10 −5	парамагнитный
платина	1+ 2,57 · 10 −4	парамагнитный
кобальт	80 … 200	ферромагнитный
утюг	300 … 10 000	ферромагнитный
Ферриты	4… 15 000	ферромагнитный
Mumetall (NiFe)	50 000 … 140 000	ферромагнитный
аморфные металлы (ферромагнетики)	700 … 500 000	ферромагнитный
нанокристаллические металлы (ферромагнетики)	20 000 … 150 000	ферромагнитный

Магнитные материалы можно классифицировать на основе их проницаемости.

Диамагнитные вещества ≤μр

Этот эффект называется эффектом Мейснера-Оксенфельда и является важной частью сверхпроводимости.μр

Парамагнитные вещества μр>1{\ displaystyle \ mu _ {\ mathrm {r}}> 1}

Для большинства материалов число проницаемости немного больше единицы (например, кислород , воздух ) — так называемые парамагнитные вещества. В парамагнетиках атомные магнитные моменты выравниваются во внешних магнитных полях и, таким образом, усиливают магнитное поле внутри вещества. Значит намагниченность положительная и значит . Температурная зависимость восприимчивости определяется законом Кюри . Парамагнетизм может иметь и другие причины, например, электроны проводимости металлов вносят не зависящий от температуры вклад (парамагнетизм Паули).μр>1{\ displaystyle \ mu _ {\ mathrm {r}}> 1}

Ферромагнитные вещества μр≫1{\ displaystyle \ mu _ {\ mathrm {r}} \ gg 1}

Ферромагнитные вещества или магнитомягкие материалы ( железо и ферриты , кобальт , никель ) имеют особое значение , поскольку они имеют числа проницаемости . Эти вещества часто используются в электротехнике ( катушка , электродвигатель , трансформатор ). Ферромагнетики выравнивают свои магнитные моменты параллельно внешнему магнитному полю, но делают это с сильным усилением. Помимо ферромагнетиков, ферримагнетики и антиферромагнетики также обладают магнитным порядком .300000>μр>300{\ displaystyle 300 \, 000> \ mu _ {\ mathrm {r}}> 300}

Намагничивание ферромагнетиков

В зависимости от магнитных свойств, то есть способности намагничиваться под действием внешнего магнитного поля, все вещества делятся на несколько классов. Которые характеризуются разной величиной относительной магнитной проницаемости μ_r и магнитной восприимчивости χ. Большинство веществ являются диамагнетиками (χ = -10-8 … -10-7 и μ_r < 1) и парамагнетиками (χ = 10-7 … 10-6 и   μ_r > 1), несколько реже встречаются ферромагнетики (χ = 103 … 105 и   μ_r >> 1). Кроме данных классов магнетиков существует ещё несколько классов магнетиков: антиферромагнетики, ферримагнетики и другие, однако их свойства проявляются только при определённых условиях.

Особый интерес в радиоэлектронике ферромагнитные вещества. Основным отличием данного класса веществ является нелинейная зависимость намагничивания, в отличие от пара- и диамагнетиков, имеющих линейную зависимость намагничивания J от напряженности Н магнитного поля.

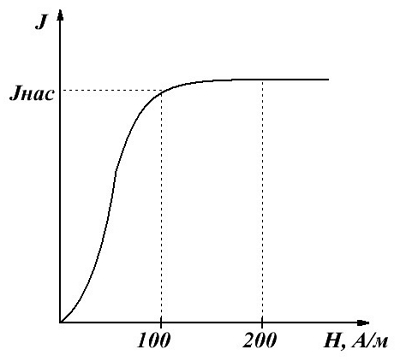
Зависимость намагничивания J ферромагнетика от напряженности Н магнитного поля.

На данном графике показана основная кривая намагничивания ферромагнетика. Изначально намагниченность  J, в отсутствие магнитного поля (Н = 0), равна нулю. По мере возрастания напряженности намагничивание ферромагнетика проходит довольно интенсивно, вследствие того что его магнитная восприимчивость и проницаемость очень велика. Однако по достижении напряженности магнитного поля порядка H ≈ 100 А/м увеличение намагниченности прекращается, так как достигается точка насыщения J_НАС. Данное явление называется магнитным насыщением. В данном режиме магнитная проницаемость ферромагнетиков сильно падает и при дальнейшем увеличении напряженности магнитного поля стремится к единице.

Проницаемость и тип магнетизма

Мы различаем диамагнитные материалы ( серебро , медь , вода , золото , свинец , цинк …), парамагнитные ( воздух , алюминий , магний , платина …) и ферромагнетики ( кобальт , железо , мю-металл , никель … )).

В общем, диамагнитные и парамагнитные материалы имеют значения относительной проницаемости, близкие к 1. Таким образом, абсолютная проницаемость диамагнитных и парамагнитных материалов практически равна проницаемости вакуума, то есть 4π × 10 -7  Гн / м.
μ{\ displaystyle \ mu}

Проницаемость ферромагнитных материалов непостоянна, но зависит от магнитного возбуждения . Для низких значений остаточное значение довольно низкое (мы говорим о пороге до того, как поле возбуждения H создаст значительную индукцию B), но оно увеличивается с увеличением значения, проходящего через максимум, и затем может снова стать унитарным при -выше другого порога. из-за насыщения (тогда мы говорим о магнитном насыщении). Поэтому в таблице мы указываем максимальные значения относительной проницаемости.
ЧАС→{\ displaystyle {\ vec {H}}}ЧАС→{\ displaystyle {\ vec {H}}}μр{\ displaystyle \ mu _ {r}}ЧАС→{\ displaystyle {\ vec {H}}}

Относительная магнитная проницаемость ферромагнитных материалов при 20  ° C

Ферромагнитные материалы	µ r (максимальное значение)	Температура Кюри в ° C
Кобальт	250	1 130
Утюг	5 000	770
Му-металл	100 000	420
Никель	600	358

Виды проницаемости и формулы

Восприимчивость к магнетизму зависит от вида среды и определяется её свойствами. Поэтому принято говорить о способности к проницаемости конкретной системы, имея в виду состав, состояние, температуру и другие исходные данные.

Существует четыре вида проницаемости:

1. Относительная. Характеризует, насколько взаимодействие в выбранной среде отличается от вакуума.
2. Абсолютная. Находится как произведение проницаемости на магнитную константу.
3. Статическая. Определяется с учётом коэрцитивной силы и магнитной индукции. При этом, чем большее значение имеет характеристика, тем меньше частота магнитных потерь. Отсюда следует, что статическая проницаемость зависит от температуры.
4. Дифференциальная. Устанавливает связь между малым увеличением индукции и напряжённости — μд = m * tgb. Это утверждение означает, что величина определяется по основной кривой намагничивания, из-за нелинейности которой она переменчивая.

Если среда однородная и изотропная, то проницаемость определяется по формуле:μ = В/(μoН), где: B — магнитная индукция; H — напряжённость; μo — константа. Постоянный коэффициент в формуле водится для записи уравнения магнетизма в рациональной форме для проведения расчётов. Знак его всегда постоянный. Он позволяет связать между собой относительную магнитную проницаемость и абсолютную.

Магнитная восприимчивость связана с проницаемостью простым выражением μ = 1 + χ. Эта формула справедлива, если все параметры будут измеряться в СИ. В единицах СГС равенство примет вид μ = 1 + 4πx. Например, проницаемость вакуума равняется единице, так как x = 0. Она безразмерна и помогает оценить способность намагничивания материала в МП.

Существует три вида восприимчивости: объёмная, удельная и молярная. Для диамагнетиков она отрицательная, а для парамагнетиков — положительная. При этом у ферромагнетиков её значения могут достигать тысяч единиц, в то время как для остальных классов веществ величина имеет очень малый порядок, около 10 -4 — 10 -6 .

Если на материал одновременно воздействует постоянное и переменное магнитное поле, то для описания процесса вводят дополнительное понятие — дифференциальную проницаемость. Наибольшее значение дифференциального параметра всегда будет превышать статическую составляющую μ = (1/μо)*(dB/dH). Эта формула по своему виду напоминает выражение, описывающее трение.

Общие сведения

В природе существует несколько видов силовых полей. Одним из них является магнитное поле (МП). В физике под ним понимают силу, действующую на перемещающиеся электрические заряды, обладающие магнитным моментом. Каждое тело в том или ином виде характеризуется восприимчивостью к такого роду полю.

Для понимания процесса можно провести эксперимент. Если взять кольцо индуктивности и пропустить через него электрический ток, то вокруг него возникнет электромагнитное поле. Если в катушку вставить железный сердечник, то магнитные свойства усилятся. Другими словами, железо усиливает магнитное поле, созданное током, протекающим по виткам. Получается, что появляется дополнительный источник магнетизма — железо. По принципу суперпозиции векторы источников складываются. Возникает усиленное поле.

Допустим, магнитная индукция поля, создаваемая только током, имеет величину B0, а веществом — B1. Вектор магнитной индукции в материале будет складываться из этих двух величин: B = B0 + B1. Основываясь на эксперименте, физики решили ввести новую величину, которая характеризует, насколько вещество изменяет магнитное поле. Этот параметр было решено обозначить символом μ и назвать магнитной проницаемостью. Её единицей измерения стала безразмерная величина.

Таким образом, физический смысл магнитной проницаемости вещества заключается в величине, равной отношению модуля вектора магнитной индукции поля в материале к создаваемому теми же токами полю без дополнительных элементов. Для вакуума формула магнитной проницаемости имеет вид μ = B / B0. По сути параметр является магнитным аналогом диэлектрической проницаемости. Но если диэлектрики всегда ослабляют поле, то магнетики его усиливают.

На протяжении нескольких десятков лет различные физики проводили эксперименты над способностью материалов поддерживать распространение МП. В результате была построена таблица, в которую были занесены показатели, характерные для разных сред. Так, для воздуха параметр равняется 1.25663753*10−6, вакуума — 4π*10−7, дерева — 1.25663760*10−6, а чистого железа — 6.3*10−3. Все эти данные общедоступны. Их легко можно найти практически в любом физическом справочнике.

Гистерезис ферромагнетиков

Еще одной особенностью ферромагнетиков является наличие петли гистерезиса, которая является основополагающим свойством ферромагнетиков.

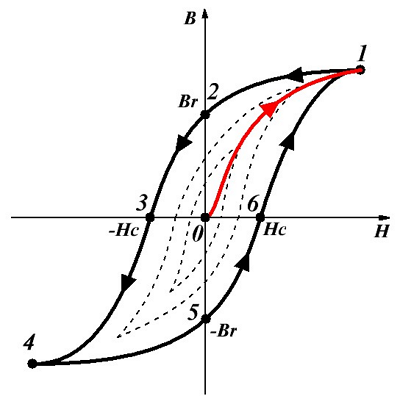
Петля гистерезиса ферромагнетика.

Для понимания процесса намагничивания ферромагнетика изобразим зависимость индукции В от напряженности Н магнитного поля, где красным цветом выделим основную кривую намагничивания. Данная зависимость довольно неопределенна, так как зависит от предыдущего намагничивания ферромагнетика.

Возьмём образец ферромагнитного вещества, которое не подвергалось намагничиванию (точка 0) и поместим его в магнитное поле, напряженность Н которого начнем увеличивать, то есть зависимость будет соответствовать кривой 0 – 1, пока не будет достигнуто магнитное насыщение (точка 1). Дальнейшее увеличение напряженности не имеет смысла, потому как намагниченность J практически не увеличивается, а магнитная индукция увеличивается пропорционально напряженности Н. Если же начинать уменьшать напряженность, то зависимость В(Н) будет соответствовать кривой 1 – 2 – 3, при этом когда напряженность магнитного поля упадёт до нуля (точка 2), то магнитная индукция не упадёт до нуля, а будет равна некоторому значению B_r, которое называется остаточной индукцией, а намагничивание будет иметь значение J_r, называемое остаточным намагничиванием.

Для того чтобы снять остаточное намагничивание и уменьшить остаточную индукцию B_r до нуля, необходимо создать магнитное поле, противоположное полю, вызвавшему намагничивание, причем напряженность размагничивающего поля должна составлять Н_с, называемая коэрцитивной силой. При дальнейшем росте напряженности магнитного поля, которое противоположно первоначальному полю, происходит насыщение ферромагнетика (точка 4).

Таким образом, при действии на ферромагнетик переменного магнитного поля зависимость индукции от напряженности будет соответствовать кривой 1 – 2 – 3 – 4 – 5 – 6 – 1, которая называется петлёй гистерезиса. Таких петель для ферромагнетика может быть множество (пунктирные кривые), называемые частными циклами. Однако, если при максимальных значениях напряженности магнитного поля происходит насыщение, то получается максимальная петля гистерезиса (сплошная кривая).

Так как магнитная проницаемость μ_r ферромагнетиков имеет довольно сложную зависимость от напряженности магнитного поля, поэтому нормируются два параметра магнитной проницаемости:

μ_н – начальная магнитная проницаемость соответствует напряженности Н = 0;

μ_max – максимальная магнитная проницаемость достигается в магнитном поле при приближении магнитного насыщения.

Таким образом, у ферромагнетиков величины B_r, Н_с и μ_н (μ_max) являются основными характеристиками, влияющими на выбор вещества в конкретном случае.

Теория это хорошо, но необходимо отрабатывать это всё практически ПОПРОБОВАТЬ МОЖНО ЗДЕСЬ

Гипотеза Ампера

С её помощью можно объяснить, почему одни вещества проявляют парамагнитные или диамагнитные свойства, а другие усиливают МП. Ампер провёл ряд экспериментов, сравнивая конфигурацию поля, создаваемого полосовым магнитом и катушкой с током. Было определено, что для полосового магнита характерна ситуация, когда линии потока выходят из северного полюса и входят в южный. Катушка же создаёт поле, похожее на конфигурацию МП постоянного полосового магнита.

Это сходство позволило Амперу предположить, что магнитные свойства веществ обусловлены тем, что внутри их существует своя проводимость, которая может убывать или возрастать в зависимости от внешних воздействующих факторов. Так, Ампер утверждал, что магнитные свойства материала объясняются существованием в его объёме микроскопических замкнутых электрических токов. Впоследствии его догадка была подтверждена. Такие токи названы молекулярными.

Другими словами, это электроны, движущиеся вокруг ядра в атоме. Для примера стоит рассмотреть гелий. В нём два электрона движутся по практически одинаковым орбитам, но только в противоположные стороны. Каждый из электронов несёт электрический заряд, создающий ток, следовательно, и поле. Если нарисовать их магнитные поля, то можно увидеть, что их направление будет противоположным: B1 + B2 = 0. Значит, атом гелия не создаёт вокруг себя МП. При помещении его во внешнее МП B0 к силе притяжения электрона прибавится сила Лоренца, направленная по радиусу от ядра.

Таким образом, сила притяжения к ядру ослабеет. Чтобы двигаться по той же самой орбите, электрону нужна меньшая скорость. Применительно ко второму электрону ситуация будет противоположной. Скорость электрона станет больше. В результате поле, создаваемое первым электроном, станет меньше, а вторым — больше. Следовательно, B1 + B2 ≠ 0. При этом гелий будет намагничиваться против внешнего поля, то есть является диамагнетиком.

Для парамагнетиков характерно то, что каждый атом обладает своим орбитальным полем. То есть атомы можно представить как витки с током. Если поля нет, направление электронов хаотичное. Причём их сумма будет равняться нулю. При помещении его во внешнее МП каждый свободный атом будет стремиться развернуться так, чтобы его нормаль была направлена по полю. Но при этом процессу мешает тепловое движение.

https://youtube.com/watch?v=4yLslpJ6pcA

ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНЫЙ КОМПЛЕКС ДЛЯ ИССЛЕДОВАНИЯ МАГНИТНЫХ ХАРАКТЕРИСТИК МАГНИТОМЯГКИХ МАТЕРИАЛОВ

Неразрушающая вихретоковая диагностика структуры, состава, физико-механических свойств ферромагнитных материалов, а также вихретоковый контроль эксплуатационных параметров изготовленных их них изделий требует знания магнитных характеристик этих материалов. При вихретоковых измерениях на получаемые результаты влияет значительное число факторов — магнитные и электрические свойства материалов, геометрические характеристики изделий, условия измерения, конструктивные особенности вихретокового датчика и т.д., при этом сами магнитные свойства обладают высокой структурной чувствительностью

В силу этого для выделения диагностируемых параметров важной задачей является разделение влияющих факторов и выделение вклада магнитных свойств. В настоящей работе описывается измерительно-вычислительный комплекс, позволяющий в автоматическом режиме определять магнитную проницаемость магнитомягких ферромагнитных материалов при различных значениях напряженности внешнего намагничивающего поля

На примере м…

Свойство ферромагнетиков

С точки зрения физики наиболее интересным материалом является ферромагнетик. Существует устройство, представляющее собой кольцо из него. На прибор равномерно в один слой намотан провод, через который протекает электрический ток. В этом торе возникает электрическое поле, совпадающее по величине с вектором МП. В результате сердечник окажется намагниченным.

Если по оси ординат отложить магнитную индукцию тела, а по оси — абсцисс тока, то можно обнаружить следующие особенности:

• в начальный момент времени график будет возрастать примерно под углом 30 градусов;
• после достижения определённой величины (1 Тл) произойдёт резкое выравнивание графика относительно B0.

Из этого можно сделать вывод, что ферромагнетик примерно в тысячу раз увеличивает магнитное поле. Выходит, что магнитная проницаемость зависит от намагничивающего поля. Если провести перпендикуляры с точки перехода графика на координатные прямые и нарисовать из неё диагональ к нулевой точке, то тангенс угла к B0 будет равняться проницаемости: μ = tg j. Оказывается, что при больших намагничивающих полях МП перестаёт расти, то есть существует магнитное насыщение.

Если взять феррит и намагнитить его, а поле размагнитить путём уменьшения поля, то линия размагничивания будет другой. При исчезновении внешнего поля ферромагнетик останется намагниченным.

На петеле можно выделить две точки:

• Bo — остаточная магнитная индукция, возникающая после снятия электрического поля;
• Bc — коэрцитивная сила, индукция противоположно направленного поля.

Ферромагнетики, которые обладают широким гистерезисом, называются жёсткими. К ним относится закалённая сталь, сплавы альнико и магнико, неодим. Но бывают и ферромагнетики, которые довольно легко перемагнитить. Их петля гистерезиса имеет узкий вид. Используют такие материалы в электродвигателях, трансформаторах. Их называют мягкими. Примеры — отожжённая сталь, пермаллой.

Конституция отношения

Если режим материала называется линейным , магнитное поле и поле магнитного возбуждения связаны в данном материале так называемым «определяющим» соотношением:
B→{\ displaystyle {\ vec {B}}}ЧАС→{\ displaystyle {\ vec {H}}}

B→знак равноμЧАС→{\ displaystyle {\ vec {B}} = \ mu \, {\ vec {H}}}

где µ — магнитная проницаемость материала. Магнитная проницаемость измеряется в генри на метр (Гн · м -1 или Гн / м).

Внимание, это конституционное отношение удобно и встречается во многих случаях, но не универсально. К ним относятся циклы гистерезиса , явления насыщения , двулучепреломляющие среды, хиральные среды, нелинейно-оптические среды и т

Д.

Магнитная проницаемость материала ( ) выражается произведением вакуумной проницаемости (которая выражается в Гн / м) и относительной проницаемости (безразмерная):
μ{\ displaystyle \ mu}μ{\ displaystyle \ mu _ {0}}μр{\ displaystyle \ mu _ {\ mathrm {r}}}

μзнак равноμμр{\ displaystyle \ mu = \ mu _ {0} \, \ mu _ {\ mathrm {r}}}.

• μ{\ displaystyle \ mu _ {0}}- универсальная постоянная, магнитная постоянная (или магнитная проницаемость вакуума), которая составляет 4π × 10-7  Гн / м
• μр{\ displaystyle \ mu _ {\ mathrm {r}}} зависит от материала.

В воздухе, вакууме, газах, меди, алюминии, земле и других материалах примерно равно 1, эти материалы не могут направлять магнитное поле.
μр{\ displaystyle \ mu _ {\ mathrm {r}}}

Диа- и пара- магнетики

Все вещества обладают определенными магнитными свойствами, т. е. являются магнетиками. Для большинства веществ магнитная проницаемость μ близка к единице и не зависит от величины магнитного поля. Вещества, для которых магнитная проницаемость незначительно меньше единицы (μ < 1), называются диамагнетиками, незначительно больше единицы (μ > 1) — парамагнетиками. Вещества, магнитная проницаемость которых зависит от величины внешнего поля и может значительно превышать единицу (μ » 1), называются ферромагнетиками.

Примерами диамагнетиков являются свинец, цинк, висмут (μ = 0,9998); парамагнетиков — натрий, кислород, алюминий (μ = 1,00023); ферромагнетиков — кобальт, никель, железо (μ достигает значения 8⋅103).

Впервые объяснение причин, вследствие которых тела обладают магнитными свойствами, дал Анри Ампер (1820 г.). Согласно его гипотезе, внутри молекул и атомов циркулируют элементарные электрические токи, которые и определяют магнитные свойства любого вещества.

Возьмем некоторое твердое вещество. Его намагниченность связана с магнитными свойствами частиц (молекул и атомов), из которых он состоит. Рассмотрим, какие контуры с током возможны на микроуровне. Магнетизм атомов обусловлен двумя основными причинами:

1) движением электронов вокруг ядра по замкнутым орбитам (орбитальный магнитный момент) (рис. 1);

2) собственным вращением (спином) электронов (спиновой магнитный момент) (рис. 2).

Для любознательных. Магнитный момент контура равен произведению силы тока в контуре на площадь, охватываемую контуром. Его направление совпадает с направлением вектора индукции магнитного поля в середине контура с током.

Так как в атоме плоскости орбит различных электронов не совпадают, то вектора индукций магнитных полей , созданные ими (орбитальные и спиновые магнитные моменты), направлены под разными углами друг к другу. Результирующий вектор индукции многоэлектронного атома равен векторной сумме векторов индукций полей, создаваемых отдельными электронами. Не скомпенсированными полями обладают атомы с частично заполненными электронными оболочками. В атомах с заполненными электронными оболочками результирующий вектор индукции равен 0.

Во всех случаях изменение магнитного поля обусловлено появлением токов намагниченности (наблюдается явление электромагнитной индукции). Иными словами принцип суперпозиции для магнитного поля остается справедливым: поле внутри магнетика является суперпозицией внешнего поля \(~\vec B_0\) и поля \(~\vec B’\) токов намагничивания i′, которые возникают под действием внешнего поля. Если поле токов намагниченности направлено так же, как и внешнее поле, то индукция суммарного поля будет больше внешнего поля (Рис. 3, а) – в этом случае мы говорим, что вещество усиливает поле; если же поле токов намагниченности направлено противоположно внешнему полю, то суммарное поле будет меньше внешнего поля (Рис. 3, б) – именно в этом смысле мы говорим, что вещество ослабляет магнитное поле.

Рис. 3

В диамагнетиках молекулы не обладают собственным магнитным полем. Под действием внешнего магнитного поля в атомах и молекулах поле токов намагниченности направлено противоположно внешнему полю, поэтому модуль вектора магнитной индукции \(~\vec B\) результирующего поля будет меньше модуль вектора магнитной индукции \(~\vec B_0\) внешнего поля.

Подробнее механизм намагничивания диамагнетиков описан здесь: Слободянюк А.И. Физика 10. §13.3 Типы магнетиков.

В парамагнетиках молекулы обладают собственным магнитным полем. В отсутствии внешнего магнитного поля из-за теплового движения вектора индукций магнитных полей атомов и молекул ориентированы хаотически, поэтому их средняя намагниченность равна нулю (рис. 4, а). При наложении внешнего магнитного поля на атомы и молекулы начинает действовать момент сил, стремящийся повернуть их так, чтобы их поля были ориентированы параллельно внешнему полю. Ориентация молекул парамагнетика приводит к тому, что вещество намагничивается (рис. 4, б).

Рис. 4

Полной ориентации молекул в магнитном поле препятствует их тепловое движение, поэтому магнитная проницаемость парамагнетиков зависит от температуры. Очевидно, что с ростом температуры магнитная проницаемость парамагнетиков уменьшается.

Дифференциальная проницаемость

В случае ферромагнетиков намагниченность обычно не зависит линейно от внешнего магнитного поля. Можно намагничивать ферромагнетики до насыщения. Из-за этого магнитного насыщения и магнитной остаточной проницаемости проницаемость также непостоянна. Для небольших полей проницаемость значительно больше, чем вблизи насыщения. Кроме того, намагниченность зависит от предыдущей намагниченности, они, как говорят, имеют память . Поведение описывается петлей гистерезиса . Определение как отношение соответствует наклону кривой намагничивания только в том случае, если оно линейное.
Б.ЧАС{\ displaystyle {\ tfrac {B} {H}}}

В зависимости от области применения используются разные определения проницаемости. Для технических приложений он определен в общей сложности одиннадцать раз с различными расчетами в DIN 1324, часть 2. В дополнение к проницаемости как частному от плотности магнитного потока в Тесла (Тл) и напряженности магнитного поля в амперах на метр (А / м), используется дифференциальная проницаемость , то есть наклон кривой гистерезиса в одном месте. .μ{\ displaystyle \ mu}Б.{\ displaystyle B}ЧАС{\ displaystyle H} μД.{\ displaystyle \ mu _ {\ mathrm {D}}}

Кривая гистерезиса

Проблема постоянной предполагаемой проницаемости видна из кривой гистерезиса . Проницаемость соответствует наклону
μД.{\ displaystyle \ mu _ {\ mathrm {D}}}

μdзнак равноdБ.dЧАС{\ displaystyle \ mu _ {\ mathrm {d}} = {\ frac {\ mathrm {d} B} {\ mathrm {d} H}}}.