Закон ома для полной цепи

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

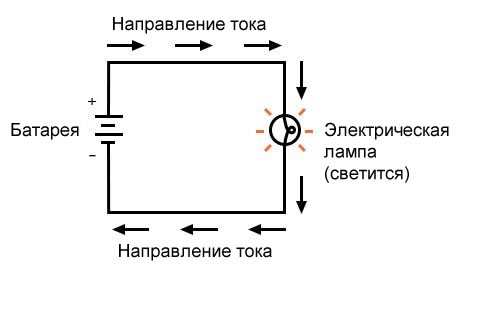Рисунок 1 – Пример простой схемы

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

Какая величина тока (I) в этой цепи?

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

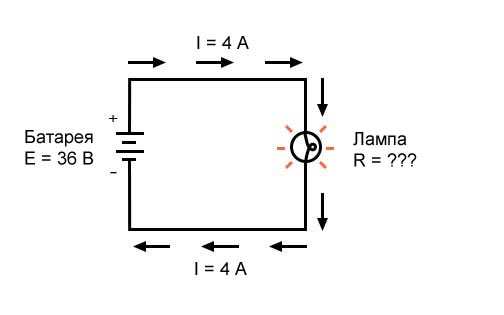Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

Какое сопротивление (R) оказывает лампа?

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

Какое напряжение обеспечивает батарея?

Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.

Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение. 

Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока). 

Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?

Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.

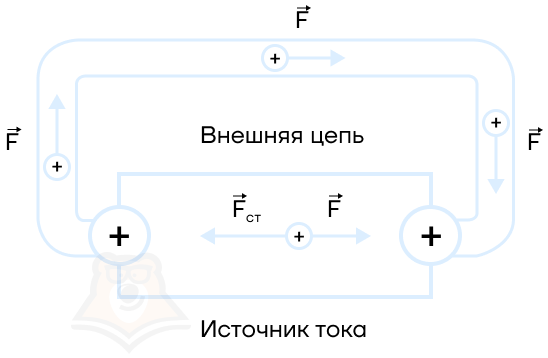
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила (\(F_{ст}\)), от плюса к плюсу) и сила электростатического поля (\(F\)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы \(F\)). 

Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению \(F_{ст}\)), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда. 

После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.

Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.

Закон Ома для участка цепи

Какой ученый променял бильярд на физику?Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.

Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.

Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и . Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:

U_r = Ir.

Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:

U_R = IR.

Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:

ε = UR+ Ur , гдеε – ЭДС источника тока (В);UR – напряжение на самой электрической цепи (В);Ur – напряжение внутри источника тока (В).

Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи: 

\(I=\frac{ε}{R + r}\) , гдеI – ток в цепи (А);ε – ЭДС источника тока (В);R – сопротивление в цепи (Ом);r – внутреннее сопротивление источника (Ом).

Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.

Где самое большое сопротивление в теле человека?Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.

Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:\(I=\frac{ε}{R + r}\),\(r=\frac{ε}{I}-R=\frac{10}{2}-4=1\) (Ом).Ответ: 1 Ом

Формула закона Ома для замкнутой цепи

Выведем формулу закона Ома для замкнутой цепи.

Сторонние силы, перемещая заряд $Δq$ за время $Δt$, совершают работу:

$$А_{ст}=\mathscr{E}q$$

Ток, по определению, равен отношению заряда, прошедшего по проводнику ко времени прохождения, то есть:

$$I={Δq\over Δt}$$

Подставив значение заряда из этой формулы в предыдущую, получим:

$$А_{ст}=\mathscr{E}IΔt$$

Вся эта работа будет выделена в виде тепла на сопротивлении цепи. Сопротивление цепи состоит из двух компонент: сопротивление самой цепи $R$ и сопротивление источника ЭДС $r$. С учетом закона Джоуля-Ленца:

$$ А_{ст}=I^2RΔt+I^2rΔt$$

Приравнивая левые части формул, получаем:

$$\mathscr{E}IΔt=I^2RΔt+I^2rΔt$$

После сокращений и преобразований имеем:

$$I={\mathscr{E}\over R+r}$$

Сила тока в замкнутой цепи равна отношению ЭДС в замкнутой цепи к сумме сопротивления цепи и внутреннего сопротивления источника ЭДС.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

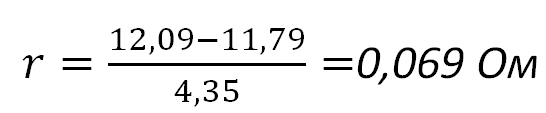
Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Работа и мощность электрического тока

Электрическое поле, создавая упорядоченное движение заряженных частиц в проводнике, выполняет работу, которую принято называть работой тока.

Работа электрического тока А — физическая величина, характеризующая: изменение электрической энергии тока — превращение ее в другие виды.
Единица работы электрического тока — джоуль, 1 Дж. В быту и технике используют также внесистемная единица — киловатт-час (кВт • ч), 1 кВт • ч = 3,6 • 106 Дж.

Если рассматривать внешний участок электрической цепи, то работа тока определяется как А = qU = UIt, где q — заряд, прошедший через поперечное сечение проводника за время t, U — электрическое напряжение на участке цепи, I — сила тока.

Если на участке цепи, по которой проходит ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет только нагрев проводников. Нагретый проводник вследствие теплообмена отдает полученную энергию в окружающую среду. Согласно закону сохранения энергии, количество выделенной теплоты равна работе тока: Q = А и вычисляется по закону Джоуля — Ленца: количество теплоты Q, выделяемой за время t в проводнике с сопротивлением R во время прохождения по нему тока силой I, равна Q = I2Rt.

Воспользовавшись законом Ома I = U/R, математически можно получить и такие формулы закона Джоуля — Ленца: Q =U2t/R и Q = UIt. Однако, если в цепи выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя.

Мощность электрического тока Р — физическая величина, характеризующая способность электрического тока выполнять определенную работу и измеряется работой, выполненной в единицу времени, Р = A/t, здесь А — работа электрического тока, t — время, за которое эта работа выполнена. Мощность во внешнем участке электрической цепи можно определить по формулам Р = UI, Р = I2R, Р = U2/R, где U — электрическое напряжение, I — сила тока, R — электрическое сопротивление участка цепи. Единица мощности — ватт, 1 Вт = 1.

Если цепь состоит из нескольких потребителей, то при параллельном их соединения общая мощность тока во всей цепи равна сумме мощностей отдельных потребителей

Это стоит принять во внимание. В быту мы пользуемся мощными электрическими приборами

Если одновременно их включить, то общая мощность может превышать ту, на которую рассчитана электрическая сеть в помещении.

Выясним, в каком случае в электрической цепи выделяется максимальная мощность. Для этого запишем закон Ома для полной цепи в таком виде: ε = IR + Ir. Умножив обе части уравнения на I, получим: εI = I 2 R + I 2 r, где εI — полная мощность, которую развивает источник тока, I2R — мощность потребителей внешней участка цепи, I2г — мощность, которую потребляет внутренняя часть круга. Итак, потребляемая мощность внешней частью цепи, составляет: P = εI – I 2 r.

График зависимости потребляемой мощности во внешней части цепи от силы тока

Графиком зависимости Р (I) является парабола, вершина которой имеет координаты {ε/2r;ε2/4r}. Из графика видно, что максимальная мощность потребляется во внешнем цепи при силе тока I = ε/2r.

Причины возникновения тока в замкнутой цепи

Причинами возникновения тока в цепи в общем случае является наличие электрического поля внутри проводника. Поле характеризуется потенциалом, следовательно, если в электрической цепи существует разность потенциалов между какими-то точками, и эти точки соединены элементами, то между ними обязательно потечет электрический ток.

Замкнутая цепь по определению — это такая цепь, которая изолирована от других цепей. А значит, в отличие от участка цепи, источник электрического поля в замкнутой цепи должен находиться внутри нее. Если такого источника не будет, то ток в замкнутой цепи возникать не сможет.

Рис. 1. Схема замкнутой электрической цепи.

Элемент цепи, который является источником электрического поля, называется источником электродвижущей силы (ЭДС).

Рис. 2. Источник ЭДС.

Таким образом, главная характеристика источника ЭДС — это величина сторонних сил. Эта величина и обозначается термином «электродвижущая сила (ЭДС)». Она обозначается символом $\mathscr{E}$ и равна отношению работы сторонних сил к перенесенному заряду:

$$\mathscr{E}={A_{ст}\over q}$$

Из данной формулы видно, что размерность ЭДС та же, что и размерность напряжения, — джоуль на кулон, или вольт.

Вторая характеристика источника ЭДС — внутреннее сопротивление. Вещество источника тока, точно так же, как и любой другой проводник, обладает некоторым электрическим сопротивлением, на котором теряется часть энергии. Физический смысл этого сопротивления такой же, как и у сопротивления проводника или нагрузки, и размерность та же — омы.

Источник ЭДС в полной цепи

Для возникновения электрического тока в замкнутой цепи, эта цепь должна содержать хотя бы один особый элемент, в котором будет происходить работа по переносу зарядов между его полюсами. Силы, переносящие заряды внутри этого элемента, делают это против электрического поля, а значит, их природа должна быть отлична от электрической. Поэтому такие силы называются сторонними.

Рис. 1. Сторонние силы в физике.

Элемент электрической цепи, в котором происходит работа сторонних сил по переносу зарядов против действия электрического поля, называется источником тока. Главная его характеристика – это величина сторонних сил. Для ее характеристики вводится специальная мера – Электродвижущая Сила (ЭДС), она обозначается буквой $\mathscr{E}$.

Значение ЭДС источника тока равно отношению сторонних сил по переносу заряда к величине этого заряда:

$$\mathscr{E}={A_{ст}\over q}$$

Поскольку смысл ЭДС очень близок к смыслу электрического напряжения (напомним, напряжение – это отношение работы, совершаемой электрическим полем, переносящим заряд, к величине этого заряда), то ЭДС так же, как и напряжение, измеряется в Вольтах:

$$1В={Дж\overКл}$$

Второй важнейшей электрической характеристикой реального источника тока является его внутреннее сопротивление. При переносе зарядов между клеммами происходит их взаимодействие с веществом источника ЭДС, а поэтому, источник для электрического тока также представляет некоторое сопротивление. Внутреннее сопротивление, как и обычное сопротивление, измеряется в Омах, но обозначается малой латинской буквой $r$.

Рис. 2. Примеры источников тока.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ).

К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.

Резистор

Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.

Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.

Вот так резистор изображается на схемах:

В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.

Вот так резистор выглядит в естественной среде обитания:

Полосочки на нем показывают его сопротивление.

На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:

О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

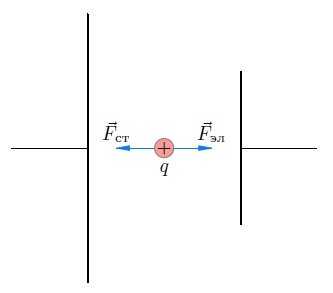
Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила

Обозначим через

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем  галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Говорим о напряжении

Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду

Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).

Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.

На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления

Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).

В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

Схема для иллюстрации закона Ома

Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.

Амперметр

Для измерения параметра используют амперметр. Этот прибор включают в разрыв цепи, чтобы обеспечить прохождение тока через рабочий элемент. Простейшие стрелочные устройства постепенно вытесняются цифровыми. Для измерения сильных токов показания снимают с помощью специального шунта, который устанавливается параллельно.

Электрический ток

По проводам течет электрический ток. Причем он именно «течет», практически как вода. Представим, что вы — счастливый фермер, который решил полить свой огород из шланга. Вы чуть-чуть приоткрыли кран, и вода сразу же побежала по шлангу. Медленно, но все-таки побежала.

Сила струи очень слабая. Потом вы решили, что напор нужен побольше и открыли кран на полную катушку. В результате струя хлынет с такой силой, что ни один помидор не останется без внимания, хотя в обоих случаях диаметр шланга одинаков.

А теперь представьте, что вы наполняете два ведра из двух шлангов. У одного из них напор сильнее, у другого слабее. Быстрее наполнится то ведро, в которое льется вода из шланга с сильным напором. Все дело в том, что объем воды за равный промежуток времени из двух разных шлангов тоже разный. Иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.

Если мы возьмем проводник с током, то будет происходить то же самое: заряженные частицы будут двигаться по проводнику, как и молекулы воды. Если больше заряженных частиц будет двигаться по проводнику, то «напор» тоже увеличится.

Электрический ток — это направленное движение заряженных частиц.

Сила тока

Сразу возникает потребность в величине, которой мы будем «напор» электрического тока измерять. Такая, чтобы она зависела от количества частиц, которые протекают по проводнику.

Сила тока — это физическая величина, которая показывает, какой заряд прошел через проводник.

Сила тока I = q/t I — сила тока q — заряд t — время

Сила тока измеряется в Амперах. Единица измерения выбрана не просто так.

Во-первых, она названа в честь физика Андре-Мари Ампера, который занимался изучением электрических явлений. А во-вторых, единица этой величины выбрана на основе явления взаимодействия двух проводников.

Здесь аналогии с водопроводом провести, увы, не получится. Шланги с водой не притягиваются и не отталкиваются вблизи друг друга (а жаль, было бы забавно).

Когда ток проходит по двум параллельным проводникам в одном направлении, проводники притягиваются. А когда в противоположном направлении (по этим же проводникам) — отталкиваются.

За единицу силы тока 1 А принимают силу тока, при которой два параллельных проводника длиной 1 м, расположенные на расстоянии 1 м друг от друга в вакууме, взаимодействуют с силой 0,0000002 Н.

Задача

Найти силу тока в цепи, если за 2 секунды в ней проходит заряд, равный 300 мКл.

Решение:

Возьмем формулу силы тока

I = q/t

Подставим значения

I = 300 мКл / 2 с = 150 мА

Ответ: сила тока в цепи равна 150 мА

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

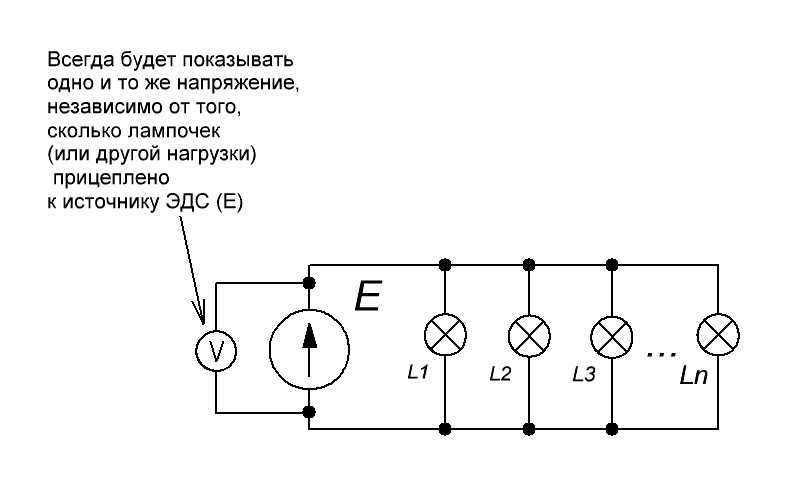
Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Особенности использования формулы

В формулировку закона Ома для замкнутой цепи входит только одно сопротивление и одно значение ЭДС. Однако в реальных цепях много элементов, и возможны несколько источников ЭДС. В этом случае используется эквивалентное сопротивление цепи, которое находится по специальным формулам преобразования цепей. В качестве значения внутреннего сопротивления используется сумма сопротивлений источников. А в качестве значения ЭДС используется алгебраическая сумма ЭДС источников.

Если цепь очень сложна и составлена из многих узлов, связанных в сложное «кружево», для нахождения тока по такой цепи используются законы Кирхгофа и составление систем уравнений.

Рис. 3. Законы Кирхгофа.

Что мы узнали?

Закон Ома для замкнутой цепи гласит, что сила тока в ней равна отношению ЭДС к сумме сопротивления цепи и внутреннего сопротивления источника ЭДС. Если источников ЭДС несколько, то необходимо использовать сумму их внутренних сопротивлений и алгебраическую сумму ЭДС.

1. /10

   Вопрос 1 из 10

Реостат

Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

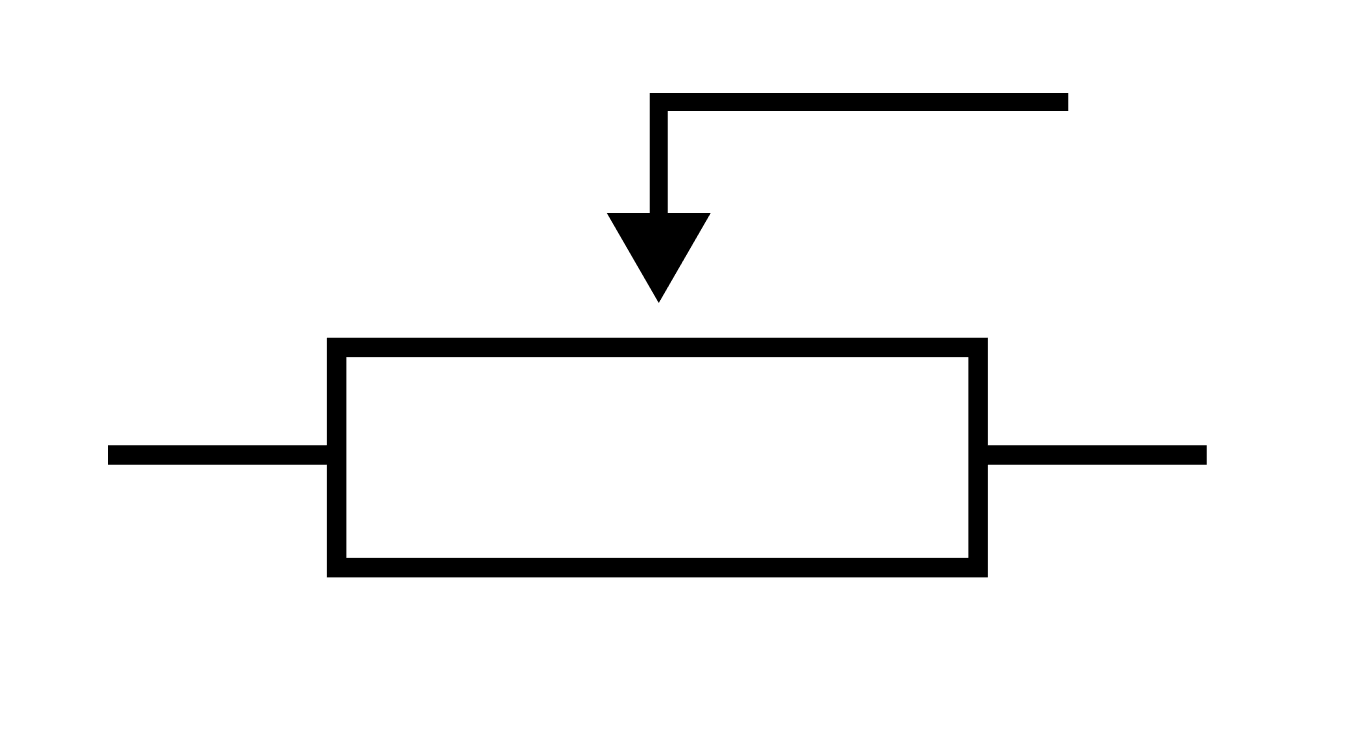
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.

По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:

Сопротивление R = ρ · l/S R — сопротивление l — длина проводника S — площадь поперечного сечения ρ — удельное сопротивление [Ом · мм2/м]