Вектор плотности потока энергии волны поток энергии

Стоячие волны

Стоячими волнами называют волны, которые образуются при наложении двух бегущих волн, которые распространяются друг навстречу другу и имеют одинаковые амплитуды и частоты.

Если мы имеем дело с двумя плоскими волнами, распространяющимися навстречу друг другу по оси X без затухания, то уравнение стоячей волны можно записать как:

где $k=\frac$ — волновое число. Уравнение (5) получено при учете, что начало координат выбирается точка, в которой обе встречные волны имеют одинаковую фазу, начало отсчета такое, что при $t=0,\ $ фазы волн равны нулю. Формула (5) показывает, что в стоячей волне амплитуда зависит от координаты ($x$).

К особенностям стоячих волн в сравнении с бегущими волнами, относят то, что:

• в стоячей волне амплитуды колебаний различны в разных точках; система имеет узлы и пучности колебаний;
• на отрезке участка системы от одного узла до соседнего, все точки вещества совершают колебания в одинаковой фазе; при переходе к соседнему участку фазы колебаний изменяются на противоположные;
• в стоячей волне нет одностороннего переноса энергии, но на каждом отрезке линии, равном $\frac$ запасена некоторая электромагнитная энергия, и она периодически переходит из энергии электрического поля в энергию магнитного поля.

Плотность потока энергии волны. Интенсивность волны

Распространение волн всегда связан с переносом энергии, который количественно характеризуется потоком энергии Ф, плотностью потока энергии J и интенсивностью волны I.

Рассмотрим волну, распространяющуюся вдоль оси о х со скоростью v (рис.210). Волна за время A t распространяется на расстояние, равное v • A t. Построим параллелепипед с основаниями A S, перпендикулярными оси ох, и длиной v — At.

Вся энергия волны, заключённая в параллелепипеде, за интервал времени A t пройдёт через правое основание A S. Обозначим энергию, переносимую волной сквозь площадку A S, через A W. Она равна произведению объёмной плотности полной энергии со _пол волны на объём параллелепипеда А V.,

Если объём V,, параллелепипеда мал, то объёмную плотность энергии со _пол волны можно считать одинаковой во всех точках рассматриваемого объёма.

Количество энергии, переносимое волной за единицу времени через поверхность AS, расположенную перпендикулярно направлению распространения волны, называется потоком Ф энергии волны

Поток энергии Ф в системе СИ измеряется в ваттах

(7 Вт =1 Л ж ). Поток энергии Ф волны может изменяться от одной

точки среды к другой. В этом случае используется векторная величина, называемая вектором плотности потока энергии J. Он был введён в 1874 г. профессором Московского университета Н. А. Умовым, поэтому назван вектором Умова.

Вектор Умова (вектор плотности потока энергии J) численно равен энергии, переносимой волной через единичную площадку, расположенную перпендикулярно направлению потока энергии в данной точке среды, за единицу времени

Запишем уравнение (20.56) в векторной форме

Вектор Умова, как и объёмная плотность полной энергии со ,_Ю1 волны, может иметь разные значения в разных точках пространства. В рассматриваемой точке среды вектор Умова изменяется со временем по такому же закону, как и объёмная плотность полной энергии со ,_Ю1 волны. Поэтому величина плотности потока энергии У через любую площадку (х = с о п s t), расположенную перпендикулярно направлению распространения волны, со временем периодически возрастает от нуля (У = 0) до максимального значения (У = У _тах).

В теории волн используется понятие среднего значения

плотности потока энергии за период времени Т (Т = xIL) в

где _пош) — среднее за период Т значение объёмной плотности

определённой точке пространства (х = с о п s t), которое назвали интенсивностью волны I

энергии волны в данной точке среды.

Подставим в (20.59) формулу (20.53)

Здесь учли, что среднее значение квадрата синуса за период Т равно 1.

Запишем формулу для интенсивности I волны, принимая во внимание выражение (20.60)

Отсюда следует, что интенсивность I волны прямо пропорциональна квадрату амплитуды А

Когда волна распространяется в трёхмерном пространстве, то поток энергии Ф через произвольную поверхность S определяется по формуле

где d S = п ? d S, п нормаль к поверхности S.

Плотность потока энергии J и интенсивность I в системе СИ

имеют размерность — ватт на квадратный метр | ^ т ].

Проведём две волновые поверхности в виде сфер, с радиусами г; и г₂. Считаем, что энергия волны не поглощается средой, тогда средние значения энергии, проходящей через волновые поверхности, равны

где S/, S₂ — площади сфер радиусами Г/ и г₂. Подставим в (20.62) интенсивности //, 1₂

сократив на р, у, со , получим

Итак интенсивность I сферической волны убывает по мере удаления от точечного источника по закону

где I 00), I (г) — интенсивность волны на расстояниях г = 1 м и произвольном расстоянии г от источника волны. Уравнение (20.65) следует из (20.63) и (20.64), записанных для двух расстояний г = 1 м и г > 1 м.

Зависимость амплитуды А и интенсивности I сферической волны от расстояния г от источника волны объясняются тем, что по мере удаления фронта волны от источника волн в колебательное движение за равные промежутки времени вовлекаются всё возрастающие объёмы среды.

Уравнение сферической волны записывается в виде

где г — расстояние от источника волн до рассматриваемой точки среды.

Интенсивность I и амплитуда А плоской волны, распространяющейся в среде, не поглощающей энергию волны, не изменяются при удалении от источника волн. Это связано с тем, что в колебательное движение за равные промежутки времени вовлекаются равные объёмы среды.

Интенсивность I плоской волны, распространяющейся в поглощающей среде вдоль положительного направления оси о х, изменяется, как и амплитуда волны по экспоненциальному закону

где I () — интенсивность волны в точке х = О, а — линейный коэффициент поглощения упругих волн.

Плотность энергии электромагнитной волны. Вектор Пойнтинга. Опыт Лебедева

Электромагнитные волны переносят в пространстве энергию. Энергия электромагнитного поля W — это количественная характеристика электромагнитного взаимодействия:

где iv — объемная плотность энергии поля. Объемная плотность w энергии электромагнитного поля складывается из объемных плотностей w_e и w_m электрического и магнитного полей и, если среда не содержит сегнето- электриков и ферромагнетиков, определяется так:

I

где Е и Н — соответственно напряженности электрического и магнитного полей волны в произвольный момент времени в данной точке пространства.

Так как из выражения (20.4), то

Формулы (20.8) и (20.9) характеризуют плотность энергии электромагнитной волны в любой момент времени в любой точке пространства.

Вектор П плотности потока энергии электромагнитной волны называется вектором Пойнтинга (Умова — Пойнтинга):

По модулю вектор П определяет энергию, переносимую волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны:

где v — фазовая скорость волны, равная скорости переноса энергии (при отсутствии дисперсии). Направление вектора П совпадает с направлением переноса энергии, т.е. с направлением распространения электромагнитной волны.

Единица плотности потока энергии электромагнитной волны в СИ —

ватт на метр в квадрате (Вт/м 2 ).

Если исходить из представлений о локализации электромагнитной энергии в пространстве, то можно заключить, что она будет изменяться в данном объеме V как за счет ее вытекания из объема через поверхность S, так и за счет того, что поле передает свою энергию веществу (заряженным частицам), т.е. производит работу над веществом.

Согласно теореме Пойнтинга, убыль энергии W электромагнитного поля, заключенного в объеме V, за единицу времени определяется как

где П — вектор Пойнтинга; И — наружная нормаль к поверхности S; dS и dV — элементы поверхности и объема соответственно; j — плотность тока; Ё — напряженность электрического поля. Интеграл фп-яй^ опре-

деляет поток энергии, переносимый электромагнитным полем сквозь замкнутую поверхность S, ограничивающую рассматриваемый объем V.

Интеграл J j ? EdV описывает работу, совершаемую сторонними ЭДС над

токами проводимости, и джоулевы потери — потери энергии электромагнитного поля за счет ее преобразования в энергию теплового движения среды.

Скалярная величина /, равная модулю среднего значения вектора Пойнтинга, называется интенсивностью электромагнитной волны:

Из (20.11) следует, что интенсивность плоской гармонической электромагнитной волны пропорциональна квадрату амплитуды ее электрической составляющей:

Опыт Лебедева. Максвелл теоретически показал, что электромагнитные волны, отражаясь или поглощаясь в телах, на которые они падают, оказывают на них давление. Это давление возникает в результате воздействия магнитного поля волны на электрические токи, возбуждаемые электрическим полем той же волны. Давление электромагнитной волны на тело определяется выражением

где р — коэффициент отражения электромагнитной волны’, это отношение интенсивности отраженной волны к интенсивности падающей (при полном отражении р = 1, при полном поглощении р = 0); (w) — среднее за период волны значение объемной плотности энергии электромагнитного поля. Если волна падает на поверхность тела наклонно, под углом 0 к нормали, то (w) = (7cos0)/c.

Давление электромагнитного излучения обычно очень мало. Например, давление солнечного излучения на Земле составляет около К)- 6 Па, что в 10 10 раз меньше атмосферного давления. Экспериментальное доказательство существования давления электромагнитных волн, подтвердившее теорию Максвелла, было получено П. Н. Лебедевым. В 1899 г. он обнаружил и измерил давление света на твердые тела, а в 1910 г. — на газы. В эксперименте, выполненном в 1899 г., объект исследования имел вид подвижного крылышка. Лебедев обнаружил поворот этого крылышка под действием падающего на него света. Величина светового давления оказалась соответствующей формуле (20.15).

Давление света играет большую роль в астрофизике и атомных явлениях. Например, наряду с давлением газа давление света обеспечивает стабильность звезд, противодействуя силам гравитации.

Примеры задач на вектор Пойнтинга стоячей волны

Задание. Вычислите вектор Пойнтинга для стоячей электромагнитной волны.

Колебания полей в стоячей электромагнитной волне можно представить при помощи формул:

где $_E=2\pi \frac+?$ и $_H=2\pi \frac+\eta $\textit — запаздывание по фазе отраженной волны соответствующих полей; $?$ и $\eta $ — изменения фазы при отражении, они равны нулю или $\pi ;;$ $l$ — для свободных волн расстояние между излучателем и отражающей поверхностью.

Решение.Прежде всего, введем обозначения:

Тогда заданную систему уравнений (1.1) можно переписать как:

где амплитуды $E_1$ и $H_1$ не зависят от времени. Предположим, что $?=\pi ,\ $тогда $\eta =0$ в результате имеем:

Для электромагнитной волны, в которой $\overline\bot $ $\overline\ $следовательно:

Задание. Чему равна средняя величина по времени вектора Пойнтинга в стоячей электромагнитной волне?

Решение. Для ответа на поставленный вопрос воспользуемся ответом предыдущего примера:

Мы получили, что поток электромагнитной энергии в стоячей волне описывает выражение (2.1). Из формулы (2.1) видно, что величина $S$ совершает колебания с частотой $2\omega $ и периодически изменяет знак, следовательно, среднее от вектора Пойнтинга равно:

Формула (2.2) означает, что в стояче волне нет течения энергии. Периодическое изменение знака вектора Пойнтинга показывает, что направление движения энергии периодически изменяется. Энергия совершает колебания между пучностями электрического и пучностями магнитного полей.

Презентация на тему: » Энергия упругой волны Вектор Умова Уравнение сферической волны.» — Транскрипт:

1

Энергия упругой волны Вектор Умова Уравнение сферической волны

2

Упругая деформация. Выделим в среде, в которой распространяется упругая продольная волна, малый объем с основанием и высотой.

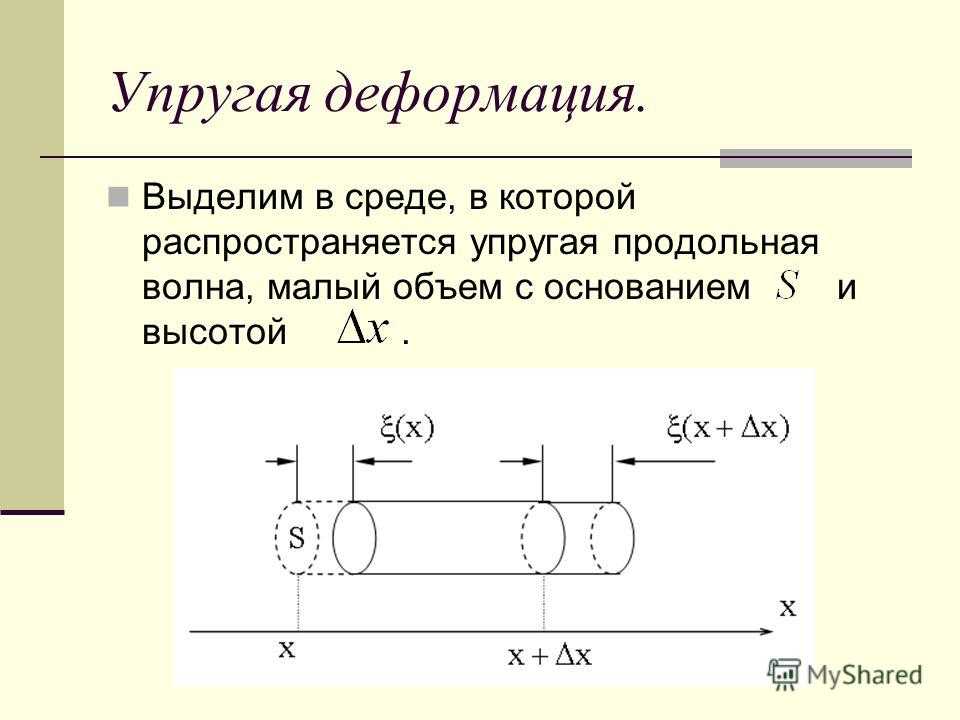
3

Упругая деформация. При распространении волны выделенный объем будет деформироваться. Относительную деформацию выделенного объема можно оценить с помощью формулы

4

Упругая деформация. При Наличие деформации свидетельствует о существовании нормального напряжения, которое определяется,где, — модуль Юнга.

5

Фазовая и колебательная скорости Фазовая скорость упругой продольной волны определяется упругими свойствами среды и ее плотностью, а колебательная скорость точек среды равна:

6

Энергия упругой волны Выделенный объем будем считать настолько малым, что и в любой точке одинаковы. Оценим энергию, которой обладает выделенный объем.

7

Энергия упругой волны Кинетическая энергия запишется в виде Потенциальная энергия выделенного объема по аналогии с энергией упруго деформированного стержня равна

8

Энергия упругой волны Полная энергия выделенного объема равна:

9

Плотность энергии упругой волны Плотность энергии упругой волны равна: Рассчитаем плотность энергии для волны

10

Плотность энергии Подставив значения производных, получим Учли, что

11

Плотность энергии Среднее по времени значение плотности энергии упругой гармонической волны Учли, что

12

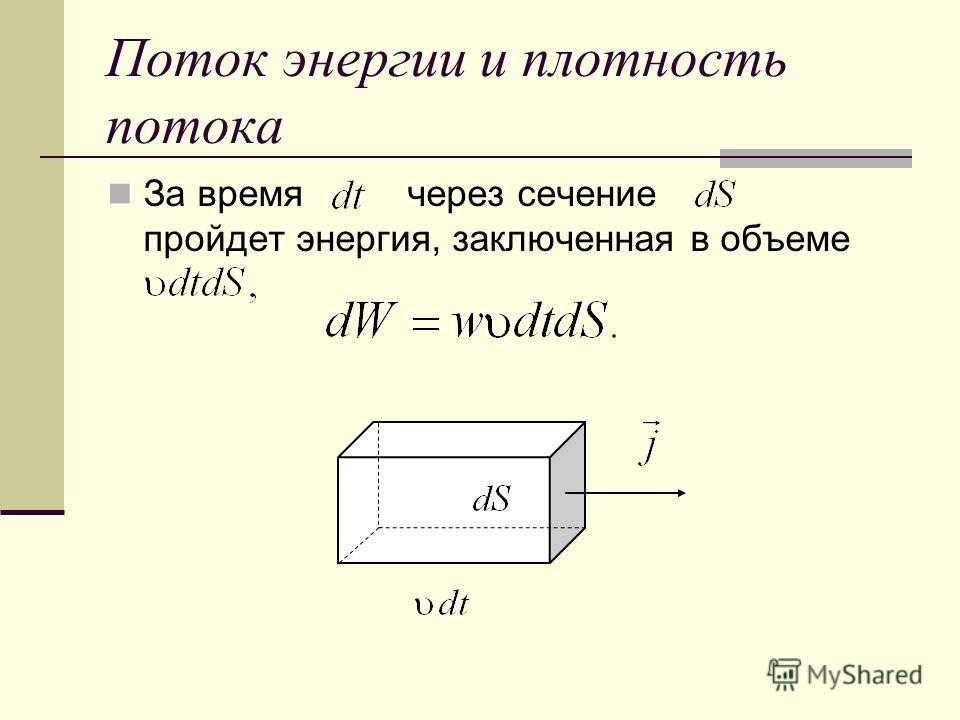
Поток энергии и плотность потока Введем новые понятия. Количество энергии, переносимое волной через поверхность в единицу времени, называется потоком энергии через эту поверхность Количество энергии, переносимое через единичную площадку, перпендикулярную к направлению распространения волны в единицу времени, называется плотностью потока

13

Поток энергии и плотность потока За время через сечение пройдет энергия, заключенная в объеме

14

Плотность потока энергии Следовательно, плотность потока энергии равна В векторной форме Вектор называется вектором Умова. Среднее значение вектора Умова называется интенсивностью волны

15

Амплитуда сферической волны Зная плотность потока в любой точке поверхности можно вычислить поток энергии через эту поверхность Найдем средний поток энергии через сферическую поверхность, что имеет место в случае сферической волны

16

Амплитуда сферической волны Если сферическая волна распространяется в изотропной не поглощающей среде, то средний поток энергии через любую поверхность должен иметь одинаковое значение Следовательно, амплитуда сферической волны равна

17

Уравнение сферической волны Фаза сферической волны Уравнение сферической волны

Стоячие волны

Стоячими волнами называют волны, которые образуются при наложении двух бегущих волн, которые распространяются друг навстречу другу и имеют одинаковые амплитуды и частоты.

Если мы имеем дело с двумя плоскими волнами, распространяющимися навстречу друг другу по оси X без затухания, то уравнение стоячей волны можно записать как:

где $k=\frac$ — волновое число. Уравнение (5) получено при учете, что начало координат выбирается точка, в которой обе встречные волны имеют одинаковую фазу, начало отсчета такое, что при $t=0,\ $ фазы волн равны нулю. Формула (5) показывает, что в стоячей волне амплитуда зависит от координаты ($x$).

К особенностям стоячих волн в сравнении с бегущими волнами, относят то, что:

• в стоячей волне амплитуды колебаний различны в разных точках; система имеет узлы и пучности колебаний;
• на отрезке участка системы от одного узла до соседнего, все точки вещества совершают колебания в одинаковой фазе; при переходе к соседнему участку фазы колебаний изменяются на противоположные;
• в стоячей волне нет одностороннего переноса энергии, но на каждом отрезке линии, равном $\frac$ запасена некоторая электромагнитная энергия, и она периодически переходит из энергии электрического поля в энергию магнитного поля.

Поток энергии и интенсивность водны. Вектор Умова

Волновой процесс связан с распространением энергии Е в пространстве. Количественной энергетической характеристикой этого процесса является поток энергии Ф — отношение энергии, перенесенной волной через некоторую поверхность, ко времени t, за которое этот перенос совершается. Если перенос энергии осуществляется равномерно, то Ф-E/t. В более общем случае поток представляет производную от энергии по времени — Ф = dE/dt. Единицей измерения потока энергии в СИ является ватт (1 Вт = 1 Дж/с).

Интенсивность (плотность потока энергии) волны I — отношение потока энергии Ф к площади S поверхности, расположенной перпендикулярно направлению распространения волны и представляющей собой поток энергии через единицу поверхности. При равномерном распределении энергии по этой поверхности I = Ф/8 = E/St; в общем случае I = с1Ф/с18. Измеряется интенсивность в Вт/м 2 .

Представим участок среды, в которой распространяется волна, в виде параллелепипеда длиной I. Площадь грани параллелепипеда, перпендикулярной направлению скорости волны v, обозначим через S (рис. 6.9).

Рис. 6.9. Связь между интенсивностью волны и скоростью ее распространения

Введем объемную плотность энергии колебательного движения w, представляющую количество колебательной энергии в единице объема среды: w-E/V. За время t через площадку S пройдет энергия, равная произведению величины объема V — IS — vtS и объемной плотности энергии:

Разделив левую и правую части этой формулы на время и площадь, получим выражение, связывающее интенсивность волны и скорость ее распространения: I = wv. Вектор I, модуль которого равен интенсивности волны, а направление совпадает с направлением ее распространения, носит название вектора Умова:

Формулу (6.32) можно представить в несколько ином виде. Учитывая, что энергия гармонических колебаний Е = —mA^cdl и масса т = pV, где р — плотность 2

вещества; V — объем вещества, получим выражение для объемной плотности энергии волны:

Теперь формула (6.32) принимает вид

Итак, интенсивность механической волны прямо пропорциональна скорости ее распространения, квадрату амплитуды колебаний частиц среды и квадрату частоты колебаний.

Примеры задач на вектор Пойнтинга стоячей волны

Задание. Вычислите вектор Пойнтинга для стоячей электромагнитной волны.

Колебания полей в стоячей электромагнитной волне можно представить при помощи формул:

где $_E=2\pi \frac+?$ и $_H=2\pi \frac+\eta $\textit — запаздывание по фазе отраженной волны соответствующих полей; $?$ и $\eta $ — изменения фазы при отражении, они равны нулю или $\pi ;;$ $l$ — для свободных волн расстояние между излучателем и отражающей поверхностью.

Решение.Прежде всего, введем обозначения:

Тогда заданную систему уравнений (1.1) можно переписать как:

где амплитуды $E_1$ и $H_1$ не зависят от времени. Предположим, что $?=\pi ,\ $тогда $\eta =0$ в результате имеем:

Для электромагнитной волны, в которой $\overline\bot $ $\overline\ $следовательно:

Задание. Чему равна средняя величина по времени вектора Пойнтинга в стоячей электромагнитной волне?

Решение. Для ответа на поставленный вопрос воспользуемся ответом предыдущего примера:

Мы получили, что поток электромагнитной энергии в стоячей волне описывает выражение (2.1). Из формулы (2.1) видно, что величина $S$ совершает колебания с частотой $2\omega $ и периодически изменяет знак, следовательно, среднее от вектора Пойнтинга равно:

Формула (2.2) означает, что в стояче волне нет течения энергии. Периодическое изменение знака вектора Пойнтинга показывает, что направление движения энергии периодически изменяется. Энергия совершает колебания между пучностями электрического и пучностями магнитного полей.

Механические волны. Уравнение волны. Вектор умова

Механические волны — процесс распространения механических колебаний в среде (жидкой, твердой, газообразной).

Следует запомнить, что механические волны переносят энергию, форму, но не переносят массу.

Важнейшей характеристикой волны является скорость ее распространения. Волны любой природы не распространяются в пространстве мгновенно, их скорость конечна.

Различают два вида механических волн: поперечные и продольные.

1. Поперечные волны:

Волны называются поперечными, если частицы среды колеблются перпендикулярно (поперек) лучу волны. Они существуют в основном за счет сил упругости, возникающих при деформации сдвига, а поэтому существуют только в твердых средах.

На поверхности воды возникают поперечные волны, так как колеблется граница сред.

В поперечных волнах различают горбы и впадины.

Длина поперечной волны — расстояние между двумя ближайшими горбами или впадинами.

2. Продольные волны:

Волны называются продольными, если частицы среды колеблются вдоль луча волны. Они возникают за счет деформации сжатия и напряжения, поэтому существуют во всех средах.

В продольных волнах различают зоны сгущения и зоны разряжения.

Длина продольной волны — расстояние между двумя ближайшими зонами сгущения или зонами разряжения.

Интенсимвность — скалярная физическая величина, количественно характеризующая поток энергии, переносимой волной в некотором направлении. Численно интенсивность равна количеству энергии, переносимому через единичную площадку, расположенную перпендикулярно направлению потока энергии, усреднённому за период волны. В математической форме это может быть выражено следующим образом:

Численное значение вектора плотности потока энергии определяется следующим образом:

Где — энергия, переносимая за время через площадку , перпендикулярную к направлению переноса энергии. Другими словами, этот вектор численно равен мощности передаваемой через единичную нормальную к направлению распространения энергии площадку. Направление вектора совпадает с направлением распространения энергии волны.

Через площадку за время будет перенесена энергия заключенная в цилиндре с основанием и высотой (v — фазовая скорость волны, рис.4). Если размеры цилиндра достаточно малы (за счет малостии) для того, чтобы плотность энергии во всех точках цилиндра можно было считать одинаковой, томожно найти как произведение плотности энергии w на объем цилиндра, равныйv, тогда

Подставив это выражение в (8.12), получим

Рассматривая фазовую скорость v как вектор, направление которого совпадает с направлением распространения волны (и переноса энергии), можно написать

Эта величина носит название вектора плотности потока энергии. Вектор плотности потока энергии был впервые введен определен русским ученым Н.А. Умовым и называется вектором Умова.

Вектор Умова, как и плотность энергии w различен в разных точках пространства. Среднее по времени значение плотности потока энергии равно:

Уравнение бегущей волны, фазовая скорость и волновое уравнение

Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846—1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распрост­ранения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то сме­щение x будет зависеть только от x и t , т. е. x = x ( x , t ).

На рис. 220 рассмотрим некоторую частицу В среды, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х=0, описываются функцией x (0, t ) = A cos w t , то частица В среды колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на t , так как для прохождения волной расстояния х требуется время t = x/v , где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид

(154.1)

откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

(154.2)

где А = const — амплитуда волны, w — циклическая частота, j — начальная фаза вол­ны, определяемая в общем случае выбором начал отсчета х и t , [ w ( t — x / v )+ j ] — фаза плоской волны.

Для характеристики волн используется волновое число

(154.3)

Учитывая (154.3), уравнению (154.2) можно придать вид

(154.4)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx .

Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде

где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е.

(154.5)

Продифференцировав выражение (154.5) и сократив на w , получим откуда

(154.6)

Следовательно, скорость v распространения волны в уравнении (154.6) есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.

Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как

(154.7)

где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/ r . Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Из выражения (154.3) вытекает, что фазовая скорость

(154.8)

Если фазовая скорость воли в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных

(154.9)

где v — фазовая скорость, — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

(154.10)