Электроемкость — основные понятия, формулы и определение с примерами

Конденсаторы постоянной и переменной емкости

Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).

Рис. 5. Конденсатор переменной емкости

Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.

Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.

Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.

Главные их преимущества электролитического конденсатора:

• высокие показатели емкости при малом объеме;
• применение в цепях с постоянным током.

Недостатки:

• необходимо соблюдать полярность;
• ограниченный срок службы;
• чувствительность к повышенным напряжениям.

Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.

Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.

Конденсаторы различных типов

Соединения конденсаторов

Для получения необходимой емкости конденсаторы соединяют между собой в батареи, применяя при этом параллельное, последовательное и смешанное соединения.

Параллельное соединение

При параллельном соединении конденсаторов одни обкладки всех конденсаторов соединяются в один узел, другие — в другой узел (рис. 5).

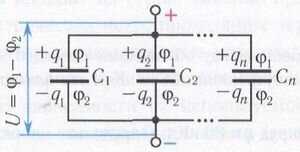
Рис. 5

Общий заряд равен алгебраической сумме зарядов каждой из обкладок отдельных конденсаторов:

\(~q = q_1 + q_2 + q_3.\)

Так как соединенные обкладки представляют собой один проводник, то потенциалы всех соединенных в один узел обкладок одинаковы и разность потенциалов между обкладками всех конденсаторов одинакова:

\(~U_1 = U_2 = U_3.\)

Так как q = C∙U, q₁ = C₁∙U, q₂ = C₂∙U, q₃ = C₃∙U, то \(~C \cdot U = C_1 \cdot U + C_2 \cdot U + C_3 \cdot U \Rightarrow\)

\(~C = C_1 + C_2 + C_3, \ C = \sum_{i=1}^n C_i .\)

Емкость батареи параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.

Если параллельно соединяют n одинаковых конденсаторов, то

\(~C = n \cdot C_1 .\)

Последовательное соединение

При последовательном соединении конденсаторов (рис. 6) потенциал соединенных между собой обкладок конденсаторов одинаков.

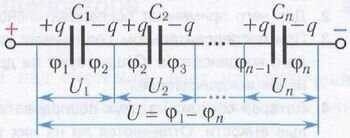
Рис. 6

Если сообщить одной из обкладок первого конденсатора заряд +q, то у второй обкладки будет заряд —q, у соседней обкладки второго конденсатора заряд +q и т.д. Следовательно,

\(~q = q_1 = q_2 = q_3.\)

Напряжение на батарее равно сумме напряжений на всех конденсаторах:

\(~U = U_1 + U_2 + U_3.\)

Так как \(~U = \dfrac qC\) ; \(~U_1 = \dfrac{q}{C_1}\) ; \(~U_2 = \dfrac{q}{C_2}\) ; \(~U_3 = \dfrac{q}{C_3}\) , то \(~\dfrac{q}{C} = \dfrac{q}{C_1} + \dfrac{q}{C_2} + \dfrac{q}{C_3} \Rightarrow\)

\(~\dfrac{1}{C} = \sum_{i=1}^n \dfrac{1}{C_i} .\)

Величина, обратная емкости батареи последовательно соединенных конденсаторов, равна сумме величин, обратных емкостям отдельных конденсаторов.

Если последовательно соединены n одинаковых конденсаторов, то \(~C = \dfrac{C_1}{n}\).

§ 22-3. Электрическая ёмкость. Электрическая ёмкость уединённого проводника

Проводники и системы, состоящие из нескольких проводников, обладают свойством накапливать электрический заряд. Какая физическая величина характеризует это свойство?

Электрическая ёмкость. Для характеристики свойства проводника накапливать электрический заряд ввели физическую величину — электрическую ёмкость С. Для объяснения физического смысла этой величины рассмотрим следующий опыт: присоединим тонким длинным проводником к стержню электрометра с заземлённым корпусом уединённый полый металлический шар.

Проводник считают уединённым, если он расположен вдали от возможных источников электрического поля как проводящих, так и непроводящих тел. Если вблизи заряженного проводника находятся другие тела, то вследствие явления электростатической индукции в проводниках происходит перераспределение свободных электрических зарядов — возникают индуцированные заряды, а в диэлектриках — смещение в противоположные стороны разноимённых зарядов, входящих в состав атомов вещества, приводящее к возникновению поляризационных зарядов. Поляризационные заряды, возникающие в диэлектриках, и заряды, индуцируемые на проводниках, создают дополнительное электростатическое поле, изменяющее потенциал заряженного проводника.

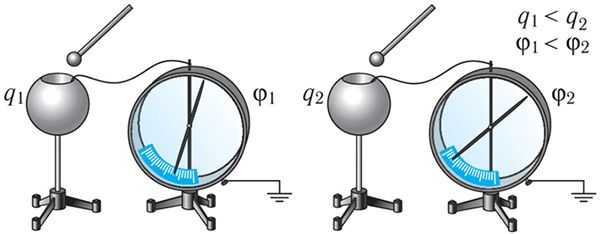Рис. 118.12

Касаясь наэлектризованным проводящим шариком, закреплённым на изолирующей ручке, внутренней поверхности полого металлического шара, будем последовательно сообщать ему одинаковые положительные электрические заряды, увеличивая его суммарный заряд в 2, 3 и т. д. раз (рис. 118.12). Чем больше сообщённый шару электрический заряд, тем больше его потенциал, так как , где R — радиус шара. Значит, во сколько раз увеличился заряд шара, во столько же раз увеличился и его потенциал, т. е. отношение электрического заряда к потенциалу остаётся величиной постоянной для данного уединённого шара: .

Прямая пропорциональная зависимость между потенциалом и электрическим зарядом справедлива не только для уединённых шарообразных проводников, но и для любого уединённого проводника произвольной формы. Необходимо только, чтобы форма и размеры проводника, а также диэлектрические свойства среды, в которой он находится, оставались неизменными.

Электрическая ёмкость уединённого проводника — физическая скалярная величина, количественно характеризующая способность проводника накапливать электрический заряд и равная отношению заряда проводника к его потенциалу:

Отметим, что электрическая ёмкость является характеристикой уединённого проводника и не зависит ни от наличия избыточного заряда, ни от его потенциала. Поскольку заряды располагаются только на внешней поверхности проводника, то ни от вещества, из которого он изготовлен, ни от его массы электроёмкость проводника также не зависит. Она зависит только от формы и размеров проводника, а также от диэлектрической проницаемости среды, в которой этот уединённый проводник находится. Например, электроёмкость уединённого проводящего шара радиусом R, находящегося в безграничной однородной среде с диэлектрической проницаемостью ε, определяют по формуле

Единицей электрической ёмкости в СИ является фарад (Ф).

1 Ф — очень большая электроёмкость. Электроёмкостью С = 1 Ф обладал бы находящийся в вакууме уединённый шар радиусом R = 9 ∙ 109 м (для сравнения: радиус земного шара R_З = 6,4 ∙ 106 м). Поэтому на практике применяют дольные единицы: микрофарад (1 мкФ = 1 ∙ 10–6 Ф), нанофарад (1 нФ = 1 ∙ 10–9 Ф) и пикофарад (1 пФ = 1 ∙ 10–12 Ф).

Например, электроёмкость такого огромного проводника, как земной шар, равна С = 0,71 мФ, а электроёмкость человеческого тела примерно С = 50 пФ.

Из истории физики

В XVII-XVIII в. учёные рассматривали электричество как нематериальную жидкость. Эта жидкость могла вливаться в проводник и выливаться из него. Так появился термин «электрическая ёмкость».

1. Какой проводник можно считать уединённым?

2. Что называют электрической ёмкостью уединённого проводника?

3. От чего зависит электроёмкость уединённого проводника?

4. Обладает ли электроёмкостью незаряженный проводник?

5. Можно ли, проанализировав формулу для расчёта электроёмкости уединённого проводника, утверждать, что его электроёмкость зависит от заряда и потенциала проводника?

6. Два проводящих заряженных шара приводят в соприкосновение. Как распределятся заряды на шарах, если один из них алюминиевый, а другой стальной и радиусы шаров одинаковые?

* Это выражение можно получить в результате математических преобразований двух формул: для нахождения электроёмкости и потенциала заряженного шара .

Энергия электростатического поля

Если к пластинам заряженного конденсатора присоединить лампочку, то она вспыхнет, а конденсатор разрядится, и электростатическое поле между его пластинами исчезнет. Следовательно, электростатическое поле конденсатора обладает энергией, которая и превратилась в световую.

Рассчитаем энергию заряженного конденсатора, заряд которого q, напряжение на конденсаторе U, емкость С.

В процессе разрядки конденсатора разность потенциалов между обкладками равномерно убывает от U до нуля, среднее же значение разности потенциалов равно \(~ \left\langle U \right\rangle = \dfrac U2\).

Тогда работа A, совершаемая электрическим полем при разряде конденсатора,

\(~A = q \cdot \left\langle U \right\rangle = \dfrac{q \cdot U}{2} = \dfrac{C \cdot U^2}{2} = \dfrac{q^2}{2C} ,\)

а энергия, которой обладает заряженный конденсатор, равна этой работе.

Этой энергией обладает электростатическое поле конденсатора. Выразим ее через характеристики поля. Подставив в формулу \(~W_e = \dfrac{C \cdot U^2}{2}\) выражение \(~C = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S}{d}\) , а также U = E∙d, имеем

\(~W_e = \dfrac{C \cdot E^2 \cdot d^2}{2} = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S \cdot E^2 \cdot d^2}{2d} = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot E^2}{2} \cdot S \cdot d = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot E^2}{2} \cdot V .\)

Энергия однородного поля пропорциональна объему, занимаемому полем. В связи с этим говорят об энергии единицы объема поля (объемной плотности энергии — ω_e). \(~\omega_e = \dfrac{W_e}{V}\). В СИ единицей объемной плотности энергии является джоуль на кубический метр (Дж/м3).

Тогда

\(~\omega_e = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot E^2}{2} .\)

Полученная формула справедлива не только для однородного электростатического поля, но и для любого другого электростатического поля, а также и для переменного электрического поля.

Конденсатор

Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.

Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.

Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара

Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.

Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.

Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:

где Q — заряд одной пластины; (φ_l— φ₂) и ∆φ — разность потенциалов между пластинами.

Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».

Пример:

Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?

Дано:Q = 50 нКл,Аφ = 2,5 кВ.	Решение Используем формулу емкости конденсатора:
С-?

Подставим значения физических величин:

Ответ: электроемкость данного конденсатора 20 пФ.

Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).

Питер ван Мушенбрук (1692-1781) — голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор — лейденскую банку и провел опыты с ней.

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки

Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.

Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.

В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.

Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком

Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.

Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов

Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.

Определение

Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.

Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.

Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.

На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.

Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.

На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.

Рис. 1. Распределение зарядов

Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.

Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.

Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.

Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.

На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.

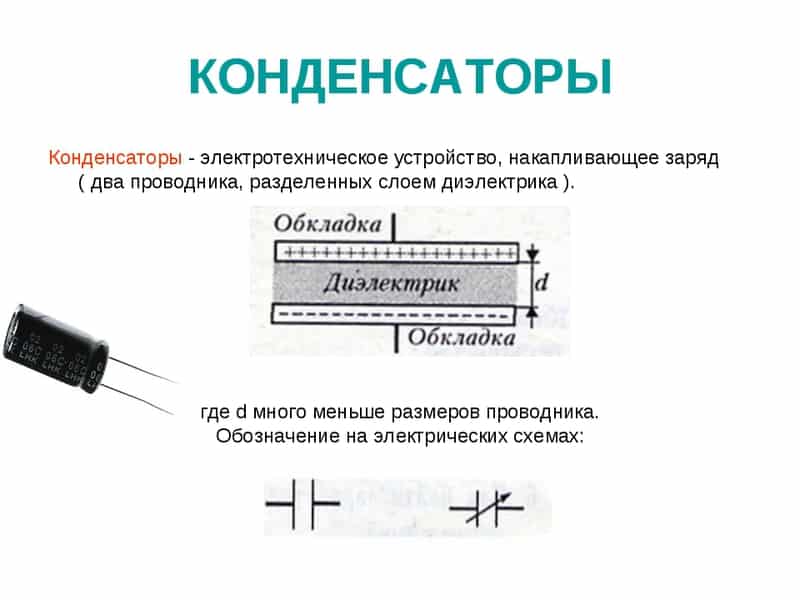
Рис. 2. Схема простого конденсатора

Существуют конденсаторы других типов:

• переменные;
• электролитические;
• оксидные;
• бумажные;
• комбинированные и другие.

Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость

Конденсаторы

Для практического использования электрической энергии необходимо уметь ее накапливать. Для этого используют специальные устройства — конденсаторы.

Конденсаторы — это устройства, которые состоят из двух или более проводников, разделенных тонким слоем диэлектрика.

Проводники, из которых состоит конденсатор, называются обкладками.

Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора понимают значение заряда положительно заряженной обкладки.

Термин «конденсатор» от латинского слова condensare — сгущать ввел А.Вольта (итальянский физик) в 1782 г. Первые электрические конденсаторы были изготовлены Э.Клейстом и П. Ван Мушенбреком в 1745 г. По имени города Лейдена, где работал Мушенбрек, французкий физик Жан Нолле назвал их лейденскими банками.

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

\(~C = \dfrac{q}{\varphi_1 — \varphi_2}\) или \(~C = \dfrac qU .\)

Из этой формулы видно, что чем больше напряжение между обкладками конденсатора, тем больше на них заряд. Но для каждого конденсатора существует предельное (максимальное) напряжение, выше которого диэлектрик начнет разрушаться. При этом заряды обкладок конденсатора мгновенно нейтрализуются, происходит пробой, т.е. конденсатор выходит из строя.

Виды конденсаторов

Конденсаторы можно классифицировать по следующим признакам и свойствам:

• по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
• по типу диэлектрика (рис. 1) —бумажные (а), воздушные (б), слюдяные, керамические, электролитические (в) и т.д.;
• по рабочему напряжению — низковольтные (напряжение пробоя до 100 В) и высоковольтные (выше 100 В);
• по возможности изменения своей емкости — постоянной емкости (см. рис. 1, а, в), переменной емкости (см. рис. 1, б), подстроечные (рис. 2).

Рис. 1

Другие виды конденсаторов показаны на рисунке 3.

См. так же Wikipedia Классификация конденсаторов

Электроемкость плоского конденсатора C зависит от площади обкладок S, расстояния между ними d и диэлектрической проницаемости диэлектрика ε, заполняющего пространство между обкладками конденсатора, но не зависит от материала, из которого эти пластины изготовлены

\(~C = \dfrac{\varepsilon_0 \cdot \varepsilon \cdot S}{d},\)

где ε — электрическая постоянная.

*Вывод формулы

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции:

\(\vec{E}=\vec{E}_{1} +\vec{E}_{2},\)

где \( E_{1} = E_{2} =\dfrac{\sigma }{2\varepsilon _{0} \cdot \varepsilon } =\dfrac{q}{2\varepsilon _{0} \cdot \varepsilon \cdot S}\) — напряженности электрических полей каждой из обкладок конденсатора, σ — поверхностная плотность заряда на обкладках конденсатора. Тогда в проекциях на ось 0Х:

справа и слева от пластин — \(E_х = 0\);

между пластин — \(E=2E_{1} =\dfrac{q}{\varepsilon _{0} \cdot \varepsilon \cdot S}.\)

Рис. 4

Электроемкость плоского конденсатора \(~C = \dfrac qU\), где \(U = E \cdot d,\) d — расстояние между пластин. Следовательно,

\(C =\dfrac{q}{E\cdot d} = \dfrac{q}{d} \cdot \dfrac{1}{E} = \dfrac{q}{d} \cdot \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{q} = \dfrac{\varepsilon _{0} \cdot \varepsilon \cdot S}{d}.\).

• При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах и т. п.
• Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
• Емкость конденсатора заметно изменяется при малейших изменениях параметра конденсатора. Так малое изменение расстояния между обкладками учитывается в измерителях малых перемещений, изменение состава диэлектрика при изменении влажности фиксируется в измерителях влажности, учет изменения высоты диэлектрика между обкладками конденсатора позволяет измерять уровень жидкости и т.п.
• Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.

Электроемкость

Электроемкость характеризует способность проводников или системы из нескольких проводников накапливать электрические заряды, а следовательно, и электроэнергию, которая в дальнейшем может быть использована, например, при фотосъемке (вспышка) и т.д.

Различают электроемкость уединенного проводника, системы проводников (в частности, конденсаторов).

Уединенным называется проводник, расположенный вдали от других заряженных и незаряженных тел так, что они не оказывают на этот проводник никакого влияния.

Электроемкость уединенного проводника — физическая величина, равная отношению электрического заряда уединенного проводника к его потенциалу\. В СИ единицей электроемкости является фарад (Ф).

1 Ф — это электроемкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Поскольку 1 Ф очень большая единица емкости, применяют дольные единицы: 1 пФ (пикофарад) = 10-12 Ф, 1 нФ (нанофарад) = 10-9 Ф, 1 мкФ (микрофарад) = 10-6 Ф и т.д.

Электроемкость проводника не зависит от рода вещества и заряда, но зависит от его формы и размеров, а также от наличия вблизи других проводников или диэлектриков. Действительно, приблизим к заряженному шару, соединенному с электрометром, незаряженную палочку (рис. 1). Он покажет уменьшение потенциала шара. Заряд q шара не изменился, следовательно, увеличилась емкость. Это объясняется тем, что все проводники, расположенные вблизи заряженного проводника, электризуются через влияние в поле его заряда и более близкие к нему индуцированные заряды противоположного знака ослабляют поле заряда q.

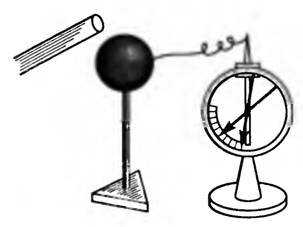
Рис. 1

Если уединенным проводником является заряженная сфера, то потенциал поля на ее поверхности \(~\varphi = \frac{q}{4 \pi \varepsilon_0 \varepsilon R}\), где R — радиус сферы, ε — диэлектрическая проницаемость среды, в которой находится проводник. Тогда

\(~C = \frac{q}{\varphi} = 4 \pi \varepsilon_0 \varepsilon R — \)

электроемкость уединенного сферического проводника.

Обычно на практике имеют дело с двумя и более проводниками. Рассмотрим систему из двух разноименно заряженных проводников с разностью потенциалов φ₁ — φ₂ между ними. Чтобы увеличить разность потенциалов между этими проводниками, необходимо совершить работу против сил электростатического поля и перенести добавочный отрицательный заряд —q с положительно заряженного проводника на отрицательно заряженный (или заряд +q с отрицательно заряженного проводника на положительно заряженный). При этом увеличивается абсолютное значение обоих зарядов: как положительного, так и отрицательного. Поэтому взаимной электроемкостью двух проводников называют физическую величину, численно равную заряду, который нужно перенести с одного проводника на другой, для того чтобы изменить разность потенциалов между ними на 1 В:

\(~C = \frac{q}{\varphi_1 — \varphi_2}. \)

Взаимная электроемкость зависит от формы и размеров проводников, от их взаимного расположения и относительной диэлектрической проницаемости среды, заполняющей пространство между ними.