Затухающие колебания

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Потери в колебательных процессах

Практически во всех колебательных процессах происходит периодический переход энергии из одного состояния в другое. Если колебания свободные, то энергия переходит, как правило, из внутренней или потенциальной энергии в кинетическую и обратно. При отсутствии потерь колебания тела происходят по гармоническому закону $x=Asin(\omega t+\varphi)$:

Рис. 1. График гармонических колебаний.

Если бы потерь энергии не было бы, такие колебания совершались бы вечно. Однако, переходы энергии всегда сопровождаются потерями. Маятник при движении испытывает трение о воздух, в результате неидеальности нити в ней также возникают неравномерные натяжения волокон, которые в результате трения нагреваются и немного разрушаются (перетираются).

3.2. Электромагнитные затухающие колебания

Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).

Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:

Падение напряжения:

— на активном сопротивлении: , где I – сила тока в контуре;

— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).

Подставим значения U_R, U_C, в уравнение, отражающее закон Кирхгофа, получим:

.

Сила тока определяется как производная от заряда , тогда , и дифференциальное уравнение примет вид:

.

Обозначим , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:

или

.

Амплитуда затухающих колебаний заряда имеет вид:

, где .

Частота затухающих колебаний в LCR – контуре:

.

Период затухающих электромагнитных колебаний:

.

Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так .

Величина называется амплитудой напряжения на конденсаторе.

Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.

Окончательное уравнение для силы тока таково:

,

где — начальная фаза.

Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

Энергия колебаний в контуре складывается из энергии электрического поля

и энергии магнитного поля

Полная энергия в любой момент времени:

где W – полная энергия контура в момент времени t=0.

Механические колебания. Свободные, затухающие и вынужденные колебания

Подробности

Обновлено 21.07.2018 11:53

Просмотров: 799

«Физика — 11 класс»

В современной физике существует специальный раздел — физика колебаний, которая занимается исследованием вибраций машин и механизмов.

Механические колебания

Механические колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Примеры колебаний: движения поршней в двигателе автомобиля, поплавка на волне, ветки дерева на ветру.

Колебательные движения, или просто колебания — это повторяющиеся движения тел.

Если движение повторяется точно, то такое движение называется периодическим.

Что является характерным признаком колебательного движения?
При колебаниях движения тела повторяются.
Так, маятник, совершив один цикл колебаний, вновь совершает такой же цикл и т.д.

Маятником называют подвешенное на нити или закрепленное на оси тело, которое может совершать колебания под действием силы тяжести Земли.

Примеры маятников:

Пружинный маятник,

2. Нитяной маятник — груз, подвешенный на нити.
В положении равновесия нить вертикальна и сила тяжести, действующая на шарик, уравновешивается силой упругости нити.

Если шарик отклонить и затем отпустить, то он начнет колебаться (качаться) из стороны в сторону.

Колебания бывают свободными, затухающими и вынужденными.

Свободные колебания.

Группу тел, движение которых изучают, называют в механике системой тел. Внутренние силы — это силы, действующие между телами системы. Внешние силы — это силы, действующие на тела системы со стороны тел, не входящих в нее.

Самый простой вид колебаний — свободные колебания.

Свободными колебаниями называются колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия и предоставлена затем самой себе.

Примеры свободных колебаний: колебания груза, прикрепленного к пружине, или груза, подвешенного на нити.

Затухающие колебания.

После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил.
Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления.
Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.

Вынужденные колебания.

Для того чтобы колебания не затухали, на тела системы должна действовать периодически изменяющаяся сила.
Постоянная сила не может поддерживать колебания, так как под действием этой силы может измениться только положение равновесия, относительно которого происходят колебания.

Вынужденными колебаниями называются колебания тел под действием внешних периодически изменяющихся сил.

Следующая страница «Условия возникновения свободных колебаний. Математический маятник»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные, затухающие и вынужденные колебания —
Условия возникновения свободных колебаний. Математический маятник —
Динамика колебательного движения. Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы

Управление затуханием колебаний

Затухание колебаний в разных случаях может являться как нежелательным, так и желательным явлением. Если затухание колебаний нежелательно – необходимо, во-первых, уменьшить потери в системе, а во-вторых, обеспечить приток энергии для компенсации потерь.

Например, пружинный маятник часов должен колебаться постоянно, и затухание в нем необходимо исключить. Для этого ось маятника устанавливается на специальном подвесе, уменьшающем трение. А кроме того, в часах имеется взведенная пружина, энергия которой через анкерный механизм передается на маятник.

Незатухающие колебания в Природе весьма редки. Например, такими колебаниями являются движение планет, где потери очень невелики. Незатухающими колебаниями можно считать океанские приливы, энергия которых постоянно пополняется за счет обращения Луны вокруг Земли.

Во многих случаях колебания системы нежелательны. Тогда затухание стремятся сделать как можно сильнее. В систему вводятся специальные устройства, характеристики которых способствуют увеличению затухания колебаний – демпфирующие элементы для приборов, амортизаторы для автомобилей и механизмов.

Рис. 3. Амортизаторы.

Что мы узнали?

Если в колебательном процессе происходит потеря энергии, то колебания затухают. Если затухание колебаний нежелательно – необходимо уменьшать потери в системе и обеспечить подвод энергии для восполнения потерь. Если затухание желательно, то в систему вводятся специальные амортизирующие и демпфирующие элементы.

1. /5

   Вопрос 1 из 5

Дифференциальное уравнение затухающих колебаний в электрическом контуре

В электрических цепях колебания затухают из-за наличия омических сопротивлений в элементах цепи. Для анализа затухающих электрических колебаний рассмотрим эквивалентную схему контура (рис. 19).

Рис. 19. Эквивалентная схема электрического колебательного контура

Электрический ток I в контуре существует благодаря кулоновским силам заряженного конденсатора С и сторонним силам, возникающим в катушке индуктивности L. В некоторый момент времени конденсатор имеет заряд q , а напряжение между его пластинами равно U. При разряде конденсатора в катушке возникает э.д.с. самоиндукции e_L, пропорциональная скорости изменения тока:

Согласно закону Ома ток в цепи:

Преобразуем уравнение (3.4) к уравнению одной переменной, а именно, — напряжения U на обкладках конденсатора.

Ток в цепи равен убыли заряда q на конденсаторе:

Заряд конденсатора равен:

Подставив формулы (3.7), (3.8) в формулу (3.4), получим

Данное дифференциальное уравнение описывает затухающие колебания напряжения на обкладках конденсатора в электрическом контуре. Решение дифференциального уравнения (3.9) имеет вид

где (3 — коэффициент затухания

со — циклическая частота затухающих колебаний

где ю — частота колебаний в отсутствии затуханий:

Период затухающих колебаний Т равен

При значении коэффициента затухания (3 = о> возникает апериодический режим разряда конденсатора (режим критического затухания). Из формул (3.12-3.14) следует, что колебания возможны лишь при условии

то есть, если

Если R > , то частота и период становятся мнимыми, колебания

не возникают, разряд конденсатора становится апериодическим. Сопротивление контура, равное

[Г

называется критическим сопротивлением. Величина, равная J—,

называется волновым сопротивлением контура.

По аналогии с механическими затухающими колебаниями введем понятие декремента затухания. Декрементом затухания называется отношение двух последующих (разделенных интервалом временем равным периоду) амплитуд колебаний:

Декремент затухания D характеризует быстроту затухания колебаний и показывает, во сколько раз уменьшается амплитуда колебаний за время, равное одному периоду. Натуральный логарифм отношения (3.18) называется логарифмическим декрементом затухания:

Логарифмический декремент X затухания колебаний в электрическом контуре будет иметь следующее выражение:

Амплитуда колебаний в контуре убывает по экспоненциальному закону:

При t = амплитуда затухающих колебаний уменьшается в

2,72 раза, (т.е., в е раз). Это время обозначается т и называется временем релаксации колебательной системы. Время релаксации колебательной системы любой природы — это время, за которое амплитуда колебаний уменьшается в е = 2,72 раза.

Из формул (ЗЛ1), (3Л -(3.20) следует

Кроме коэффициента затухания, декремента, логарифмического декремента и времени релаксации для характеристики затухающих колебаний используется понятие добротности. Добротность Q электрического контура (как и любой колебательной системы) пропорциональна отношению полной энергии колебаний W(t) к потерям энергии AW за один период Т:

Полная энергия колебательного контура равна максимальной энергии магнитного поля в катушке индуктивности:

потери энергии AW равны тепловым потерям энергии на активном сопротивлении контура R за один период колебаний:

где 1_эфф = -4L — действующее или эффективное значение силы тока в

Следовательно, добротность электрического колебательного контура будет равна:

Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие коле­бания— колебания, амплитуда которых из-за потерь энергии реальной колебатель­ной системой с течением времени умень­шается. Простейшим механизмом умень­шения энергии колебаний является ее пре­вращение в теплоту вследствие трения в механических колебательных системах,

а также омических потерь и излучения электромагнитной энергии в электриче­ских колебательных системах.

Закон затухающих колебаний опреде­ляется свойствами колебательных систем. Обычно рассматривают линейные систе­мы— идеализированные реальные систе­мы, в которых параметры, определяющие физические свойства системы, в ходе про­цесса не изменяются. Линейными система­ми являются, например, пружинный маят­ник при малых растяжениях пружины (когда справедлив закон Гука), колеба­тельный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различ­ные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что по­зволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моде­лирование, в том числе и на ЭВМ.

Дифференциальное уравнение свобод­ных затухающих колебанийлинейной системы задается в виде

где s — колеблющаяся величина, описы­вающая тот или иной физический про­цесс, d=const — коэффициент затухания,w — циклическая частота свободных не­затухающих колебаний той же колебатель­ной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотойколебательной системы.

Решение уравнения (146.1) рассмот­рим в виде

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

Решение уравнения (146.3) зависит от знака коэффициента перед искомой вели­чиной. Рассмотрим случай, когда этот ко­эффициент положителен:

w 2 =w 2 -d 2 (146.4)

(если (w 2 -d 2 )>0, то такое обозначение мы вправе сделать). Тогда получим урав­нение типа (142.1)

решением которого является функция и=Аcos(wt+j)

Таким образом, решение уравнения (146.1) в случае малых затуханий (d 2 2 )

— амплитуда затухающих колебаний,а

a— начальная амплитуда. Зависимость (146.5) показана на рис.208 сплошной линией, а зависимость (146.6) — штри­ховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда за­тухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колеба­ния не являются периодическими и, строго говоря, к ним неприменимо понятие перио­да или частоты. Однако если затухание мало, то можно условно пользоваться по­нятием периода как промежутка времени между двумя последующими максимума­ми (или минимумами) колеблющейся фи­зической величины (рис. 208). Тогда пери­од затухающих колебаний с учетом формулы

Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответству­ющих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его

— логарифмическим декрементом затуха­ния;N_e— число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротно­стиQ, которая при малых значениях лога­рифмического декремента равна

(так как затухание невелико (d 2 2 ), то Т принято равным Т).

Из формулы (146.8) следует, что до­бротность пропорциональна числу колеба­ний N_e, совершаемых системой за время релаксации.

Применим выводы, полученные для свободных затухающих колебаний линей­ных систем, для колебаний различной фи­зической природы — механических (в ка­честве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический коле­бательный контур).

1. Свободные затухающие колебания пружинного маятника.Для пружинного маятника (см. § 142) массой т, совершаю­щего малые колебания под действием уп­ругой силы F=-kx, сила трения про­порциональна скорости, т. е.

где r — коэффициент сопротивления;знак минус указывает на противоположные на­правления силы трения и скорости.

При данных условиях закон движения маятника будет иметь вид

Используя формулу w=Ök/m (см. (142.2)) и принимая, что коэффици­ент затухания

получим идентичное уравнению (146.1) дифференциальное уравнение затухающих колебаний, маятника:

Из выражений (146.1) и (146.5) вытекает, что маятник колеблется по закону

х=Aе — d t cos(wt+j) с частотой w=Ö(w 2 -r2/4m 2 ) (см. (146.4)).

Добротность пружинного маятника,

согласно (146.8) и (146.10), Q=1/rÖkm.

Затухание колебаний

То есть, с каждым колебанием часть энергии реальной системы теряется. В результате чего, амплитуда движения материальных точек постоянно становится чуть меньше. Колебания уменьшают свою амплитуду и затухают.

Потери энергии, чаще всего, пропорциональны скорости перехода энергии из одного вида в другой. Поскольку скорость перехода энергии тем больше, чем больше амплитуда колебаний, то и потери в колебательных системах тем больше, чем больше амплитуда колебаний. В высшей математике доказывается, что при таких условиях формула затухающих колебаний представляет собой синусоиду, уменьшающуюся по экспоненте – степенной функции с отрицательным показателем. Сперва затухание происходит быстро, а потом все медленнее и медленнее:

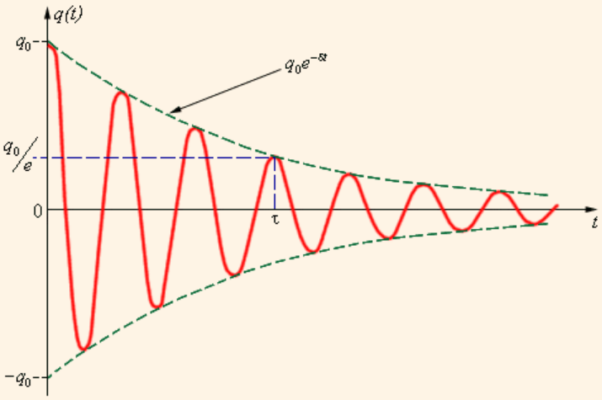Рис. 2. График затухающих колебаний.