Затухающие ⭐ колебания: виды и характеристики, частота и энергия затухающих колебаний

Характеристики затухающих колебаний

Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:

m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .

Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,

Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.

Для R L C контура применима формула с ω частотой.

При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .

При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :

Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:

Q = R L C = R ω 0 L .

R является входным сопротивлением параллельного контура.

Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:

Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.

Дифференциальное уравнение свободных затухающих колебаний (механических и электромагнитных) и его решение. Автоколебания

Рассмотрим свободные затухающие колебания— колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах,

а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухающих колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы— идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебанийлинейной системы задается в виде

где s — колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания,w — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотойколебательной системы.

Решение уравнения (146.1) рассмотрим в виде

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:

w 2 =w 2 -d 2 (146.4)

(если (w 2 -d 2 )>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (142.1)

решением которого является функция и=Аcos(wt+j)

Таким образом, решение уравнения (146.1) в случае малых затуханий (d 2 2 )

— амплитуда затухающих колебаний,а

a— начальная амплитуда. Зависимость (146.5) показана на рис.208 сплошной линией, а зависимость (146.6) — штриховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 208). Тогда период затухающих колебаний с учетом формулы

Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его

— логарифмическим декрементом затухания;N_e— число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротностиQ, которая при малых значениях логарифмического декремента равна

(так как затухание невелико (d 2 2 ), то Т принято равным Т).

Из формулы (146.8) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

Применим выводы, полученные для свободных затухающих колебаний линейных систем, для колебаний различной физической природы — механических (в качестве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический колебательный контур).

1. Свободные затухающие колебания пружинного маятника.Для пружинного маятника (см. § 142) массой т, совершающего малые колебания под действием упругой силы F=-kx, сила трения пропорциональна скорости, т. е.

где r — коэффициент сопротивления;знак минус указывает на противоположные направления силы трения и скорости.

При данных условиях закон движения маятника будет иметь вид

Используя формулу w=Ök/m (см. (142.2)) и принимая, что коэффициент затухания

получим идентичное уравнению (146.1) дифференциальное уравнение затухающих колебаний, маятника:

Из выражений (146.1) и (146.5) вытекает, что маятник колеблется по закону

х=Aе — d t cos(wt+j) с частотой w=Ö(w 2 -r2/4m 2 ) (см. (146.4)).

Добротность пружинного маятника,

согласно (146.8) и (146.10), Q=1/rÖkm.

Дифференциальное уравнение затухающих колебаний и его решение

В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

(8)

Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2b и сохранив обозначение к/m = w 2 , приведем это уравнение к виду:

(9)

Решение этого уравнения имеет вид:

(10)

Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний. Это уменьшение зависит от коэффициента затухания. Оказывается, что

(11)

Колебательный процесс может происходить лишь при условии: (w 2 — b 2 )>0, когда частота w в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w

Дата добавления: 2016-01-20 ; просмотров: 2006 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

3.2. Электромагнитные затухающие колебания

Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).

Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:

Падение напряжения:

— на активном сопротивлении: , где I – сила тока в контуре;

— на конденсаторе (С): , где q – величина заряда на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: (закон Фарадея).

Подставим значения U_R, U_C, в уравнение, отражающее закон Кирхгофа, получим:

Сила тока определяется как производная от заряда , тогда , и дифференциальное уравнение примет вид:

Обозначим , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:

или

Амплитуда затухающих колебаний заряда имеет вид:

, где .

Частота затухающих колебаний в LCR – контуре:

Период затухающих электромагнитных колебаний:

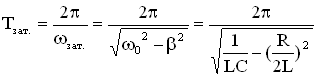Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так .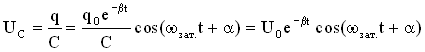

Величина называется амплитудой напряжения на конденсаторе.

Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение и векторную диаграмму.

Окончательное уравнение для силы тока таково:

где — начальная фаза.

Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

Энергия колебаний в контуре складывается из энергии электрического поля

и энергии магнитного поля

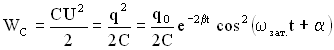
Полная энергия в любой момент времени:

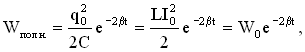
где W – полная энергия контура в момент времени t=0.

Уравнения затухающих колебаний

Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.

Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.

Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .

Функция изображается аналогично рисунку 2 .

Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .

Решение

Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:

q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .

Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение

Для нахождения I ( t ) :

I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .

Очевидно, что электрическая энергия W q запишется как:

W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .

Тогда значение магнитной энергии контура W m равняется:

W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .

Запись полной энергии будет иметь вид:

W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .

Где sin α = β ω 0 .

Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .

Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.