Что такое квазиупругая сила?

Механические колебания

теория по физике колебания и волны

Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.

Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.

Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.

Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.

Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.

Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.

Какими бывают колебания?

Напомним, что в механической системе выделяют два вида сил:

• Внутренние силы — это силы, которые возникают между телами внутри системы. Примером внутренних сил служат силы тяготения между телами солнечной системы.
• Внешние силы — силы, которые действуют на тела системы со стороны тел, которые в эту систему не входят. Примером внешней силы может стать сила ветра, под действием которой шарик, подвешенный к опоре за нить, отклоняется в сторону порыва ветра.

Свободные колебания

Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.

Колебательная система — механическая система, в которой возможно совершение свободных колебаний.

Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:

1. После выведения из равновесия в колебательной системе появляются силы, направленные в сторону положения равновесия. Эти силы стремятся возвратить систему в положение равновесия.
2. Трение между телами колебательной системы относительно мало. В противном случае колебания либо сразу затухнут, либо не начнутся совсем.

Примеры свободных колебаний:

• колебания шарика на дне сферической чаши;
• движение качелей после однократного толчка;
• колебания груза на пружине после ее растяжения;
• колебания струны после ее отклонения.

Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.

В колебательную систему математического маятника входят:

• нить;
• тело, привязанное к нити;
• Земля, в поле тяжести которой находится привязанное к нити тело.

В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.

Вынужденные колебания

Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.

Примерами вынужденных колебаний служат:

• движение поршня в цилиндре;
• раскачивание ветки дерева на ветру;
• движение иглы швейной машинки;
• движение качелей под действием постоянных толчков.

Затухающие и незатухающие колебания

Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.

Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.

Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.

Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.

Упругие и квазиупругие силы

Выясним какими силами вызываются гармонические колебания, воспользовавшись законами динамики.

По второму закону динамики сила F, действующая на материальную точку численно равна произведению массы точки m на ее ускорение w. Подставляя в это соотношение найденное ранее выражение w для гармонического колебания, определим значение силы действующей на точку в каждый момент времени. Сравнивая это уравнение с замечаем, что , где , т.е. сила, вызывающая гармонические колебания, обладает двумя важными свойствами:

1. величина силы прямо пропорциональна смещению точки от центра колебаний;
2. направление силы противоположно направлению смещений, т.е. сила всегда направлена к центру (при x>0 F 0 F

При смещении материальной точки вниз от 0 на величину x на нее будет действовать сила F_упр=-kx>0 направленная вверх, т.к. x 2 =k

Эта частота колебаний называется частотой собственных колебаний системы и обозначается w, это частота колебаний системы за счет внутренних сил.

тогда период

Частота и период не зависят от амплитуды колебаний и определяются только величинами m и k. Амплитуда и фаза колебаний (или начальная фаза j) определяются из начальных условий, при которых возникло движение.

Аналогичное гармоническое движение возникает и при движении груза m, подвешенного на пружине с учетом действия ускорения свободного падения. Отличие от рассмотренного выше случая состоит в том, что положение равновесия будет иметь место при несколько растянутой пружине. Упругая сила растяжения в положении равновесия в точности ровна силе тяжести и будет направлена вверх. Уравновешивает ее:

Чтобы материальная точка m совершала гармонические колебания не обязательно, чтобы на нее действовали именно упругие силы. Достаточно, чтобы сила при смещении от положения равновесия менялось согласно закону F=-kx.

Если сила, не являющаяся по своей природе упругой, подчиняется закону F=-mw 2 x=-kx, то она называется «квазиупругой» силой (по латыни «quasi» означает «как-бы»).

Рассмотрим пример гармонического колебательного движения под действием квазиупругих сил.

Математический маятник

Маятник настенных часов представляет собой настенный груз, который укреплен на длинном тонком стержне, подвешенном шарнирно на горизонтальной оси C перпендикулярно стержню. В первом приближении пренебрежем массой стержня и будем считать всю массу груза m сосредоточенной в его центре М. Подобная система, состоящая из материальной точки m, подвешенная на невесомом твердом стержне или нерастяжимой нити длинны СМ=L, называется математическим маятником.

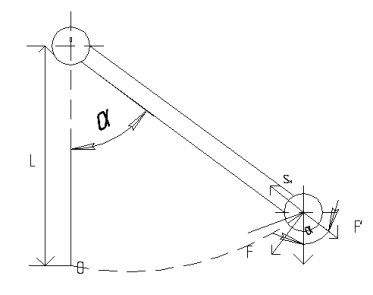
Отклоним стержень на некоторый угол a от вертикали и разложим мысленно силу веса P=mg, действующую на точку М на 2 составляющие F¢ и F, направленные соответственно вдоль стержня и перпендикулярно к нему. Сила F¢=Pcosa будет растягивать стержень и уравновесится реакцией стержня S. Неуравновешенной останется составляющая силы F=Psina. Таким образом на точку М будет действовать 2 силы P и S, направленные под углом p-a друг к другу. Равнодействующая этих сил по правилу параллелограмма будет сила F=Psina, направленная по касательной к дуге ОМ в сторону точки 0.

Когда груз придет в наинизшее положение, т.е. в точку 0, силы P и S полностью уравновесится. Таким образом точка 0 есть положение равновесия груза m. Обозначим отрезок дуги ОМ, характеризующий путь, пройденный точкой М из положения равновесия, через x и будем считать угол a и величину x положительными при отклонении стержня с грузом вправо от вертикали и отрицательными – при отклонении влево. Угол a измеряемый в радианах численно равен отношению длинны дуги x, на которую он опирается к радиусу окружности l, тогда (с учетом направления) сила F, действующая на точку М, может быть выражена в виде

Для малых углов отклонения от вертикали не превышающих 5-6°, т.е. при a

Примеры применения квазиупругой силы

1. Моделирование деформаций и разрушений материалов

Квазиупругая сила используется для моделирования деформаций и разрушений материалов в различных отраслях, таких как механическая, электронная и атомная промышленность. Например, при разработке новых материалов, которые должны выдерживать большие нагрузки, необходимо учесть квазиупругую силу, которая может приводить к деформациям и разрушению материала.

2. Исследование свойств полимеров

Квазиупругая сила применяется в исследованиях свойств полимеров, таких как упругость, прочность и вязкость. Данные исследования помогают оптимизировать процессы производства полимерных материалов и создавать новые материалы с улучшенными свойствами.

3. Проектирование спутников и космических кораблей

Квазиупругая сила играет важную роль в проектировании спутников и космических кораблей, так как она может привести к деформации и разрушению материалов в условиях космического пространства. Учитывая квазиупругую силу, инженеры могут создавать более надежные конструкции, способные выдерживать высокие нагрузки и внешние воздействия в космосе.

4. Исследования свойств кристаллов

Квазиупругая сила используется для исследования свойств кристаллов, таких как упругость и прочность. Эти данные пригодятся при создании новых материалов и устройств, таких как полупроводники, датчики и микрочипы.

Определение квазиупругой силы

Квазиупругая сила — это сила, изменяющая упругие свойства твердого тела при малых деформациях. Такие изменения происходят в результате изменений межатомных расстояний при наложении внешней нагрузки на твердое тело.

Квазиупругая сила влияет на механику твердого тела и может привести к изменению жесткости, прочности и деформируемости материала. Рассмотрение квазиупругих сил необходимо для определения точных параметров упругости материалов и разработки прочных и надежных конструкций.

Квазиупругая сила может быть определена при помощи различных методов, включая рентгеноструктурный анализ, наноиндентирование и атомно-силовую микроскопию. Эти методы позволяют измерять малые изменения структуры и свойств материалов при наложении внешних нагрузок.

Изучение квазиупругой силы является важным направлением в материаловедении и механике твердого тела. Его применение может помочь улучшить качество и долговечность материалов и конструкций, сократить время разработки новых материалов и повысить эффективность их использования в различных отраслях промышленности.