Три основные закона механики, которые были сформулированы исааком ньютоном

Момент силы. Условие равновесия рычага

Основным признаком
взаимодействия тел в динамике является возникновение ускорений. Однако часто
бывает нужно знать, при каких условиях тело, на которое действует несколько
различных сил, находится в состоянии равновесия.

Существует два вида
механического движения — поступательное движение и вращение.

Если траектории движения всех
точек тела одинаковы, то движение поступательное. Если траектории всех
точек тела — дуги концентрических окружностей (окружностей с одним центром —
точкой вращения), то движение вращательное.

Равновесие невращающихся тел:
невращающееся тело находится в равновесии, если геометрическая сумма сил,
приложенных к телу, равна нулю.

Равновесие тела, имеющего
неподвижную ось вращения

Если линия действия силы,
приложенной к телу, проходит через ось вращения тела, то эта сила
уравновешивается силой упругости со стороны оси вращения.

Если линия действия силы не
пересекает ось вращения, то эта сила не может быть уравновешена силой упругости
со стороны оси вращения, и тело поворачивается вокруг оси.

Вращение тела вокруг оси под
действием одной силы может быть остановлено действием второй силы. Опыт
показывает, что если две силы по отдельности вызывают вращение тела в
противоположных направлениях, то при их одновременном действии тело находится в
равновесии, если выполняется условие:

,
где d₁ и d₂
— кратчайшие расстояния от линий действия сил F₁и
F_2.Расстояние d
называется плечом силы, а произведение модуля силы на плечо — моментом
силы:

Если моментам сил, вызывающим
вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а
моментам сил, вызывающим вращение против часовой стрелки, — отрицательный знак,
то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила
моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если
алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси
равна нулю:

За единицу вращающего момента в
СИ принимается момент силы в 1 Н, линия действия которой находится на
расстоянии 1 м от оси вращения. Эту единицу называют ньютон-метром.

Общее условие равновесия тела: тело
находится в равновесии, если равны нулю геометрическая сумма всех приложенных к
нему сил и алгебраическая сумма моментов этих сил относительно оси вращения.

Потенциальная энергия

Потенциальная энергия —
это энергия взаимодействия тел, зависит от взаимного их расположения.

Работа силы тяжести (потенциальная
энергия тела в поле силы тяжести)

Если тело перемещается вверх,
работа силы тяжести отрицательна; вниз — положительна.

Работа силы тяжести не зависит
от траектории движения тела, а зависит лишь от перепада высот (от изменения
положения тела над поверхностью земли).

Работа силы тяжести по
замкнутому контуру равна нулю.

Силы, работа которых по замкнутому
контуру равна нулю, называются потенциальными (консервативными). В
механике потенциальными являются сила тяжести и упругая сила (в электродинамике
— сила Кулона), непотенциальными — сила трения (в электродинамике — сила
Ампера, Лоренца).

Потенциальная энергия тела в
поле силы тяжести: .

Работа потенциальной силы всегда
равна убыли потенциальной энергии: . Работа
упругой силы (потенциальная энергия упруго деформированного тела)

/* Если какая-то физическая
величина изменяется по линейному закону, ее среднее значение равно полусумме
начального и конечного значений — F_y */

Потенциальная энергия упруго
деформированного тела:

Примечания[]

↑ , с. 9
Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — 416 с. — ISBN 5-06-003117-9. (см. ISBN )
— С. 287. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
Голубев Ю. Ф. Основы теоретической механики. — М.: Изд-во МГУ, 2000. — 720 с. — ISBN 5-211-04244-1. (см. ISBN )
— С. 160. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — 319 с. — ISBN 5-95052-041-3. (см. ISBN )
— С. 9. «Масса полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
↑ , с. 26—28
↑ , с. 24—26
Сивухин Д. В. Общий курс физики. Т. I. Механика. — М.: Наука, 1979. — 520 с. (см. ISBN )
— С. 71.
, с. 14—16
Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — 572 с. (см. ISBN )
— С. 254. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — 248 с. (см. ISBN )
— С. 41. «В ньютоновской механике… m=const и dp/dt=ma».
Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — New York: McGraw-Hill, 1973. — 546 p. — ISBN 0-07-035048-5. (см. ISBN )
— P. 112. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
, с. 210

Закон сохранения полной механической энергии

Полная механическая энергия —
сумма кинетической и потенциальной энергии всех тел, входящих в систему:

По теореме о кинетической
энергии работа всех сил, действующих на все тела .
Если в системе все силы потенциальные, то справедливо утверждение: . Следовательно:

Полная механическая энергия
замкнутой системы есть величина постоянная (если в системе действуют только
потенциальные силы). Если в системе есть силы трения, то можно применить
следующий прием: силу трения назначаем внешней силой и применяем закон изменения
полной механической энергии: . Работа
внешней силы равна изменению полной механической энергии системы.

Вращение с ускорением

Если сформулированный Ньютоном закон механики применить к движению вращения, то получится следующее выражение:

Здесь M — момент импульса — это величина, которая показывает возможность силы совершить поворот в системе. Момент силы вычисляется, как произведение векторное силы на радиус-вектор, направленный от оси к точке приложения. Величина I — это момент инерции. Как и момент силы, он зависит от параметров вращающейся системы, в частности, от геометрического распределения массы тела относительно оси. Наконец, величина α — это угловое ускорение, позволяющее определить, на сколько радиан в секунду меняется угловая скорость.

Если внимательно посмотреть на записанное уравнение и провести аналогию между его величинами и показателями из второго ньютоновского закона, то мы получим полное их тождество.

Вес тела. Невесомость

Вес тела — сила, с
которой тело давит на опору или подвес вследствие притяжения этого тела к
земле. Вес тела приложен к опоре (подвесу). Величина веса тела зависит от того,
как движется тело с опорой (подвесом).

Вес тела, т.е. сила, с которой
тело действует на опору, и сила упругости, с которой опора действует на тело, в
соответствие с третьим законом Ньютона равны по абсолютному значению и
противоположны по направлению.

Если тело находится в покое на
горизонтальной опоре или равномерно движется, на него действуют только сила
тяжести и сила упругости со стороны опоры, следовательно вес тела равен силе
тяжести (но эти силы приложены к разным телам):

При ускоренном движении вес тела
не будет равен силе тяжести. Рассмотрим движение тела массой m
под действием сил тяжести и упругости с ускорением. По 2-му закону Ньютона:

Если ускорение тела направлено
вниз, то вес тела меньше силы тяжести; если ускорение тела направлено вверх, то
все тела больше силы тяжести.

Увеличение веса тела, вызванное
ускоренным движением опоры или подвеса, называют перегрузкой.

Если тело свободно падает, то из
формулы * следует, что вес тела равен нулю. Исчезновение веса при движении
опоры с ускорением свободного падения называется невесомостью.

Состояние невесомости
наблюдается в самолете или космическом корабле при движении их с ускорением
свободного падения независимо от скорости их движения. За пределами земной
атмосферы при выключении реактивных двигателей на космический корабль действует
только сила всемирного тяготения. Под действием этой силы космический корабль и
все тела, находящиеся в нем, движутся с одинаковым ускорением; поэтому в
корабле наблюдается явление невесомости.

Движение тела под действием сил
тяжести. Движение искусственных спутников. Первая космическая скорость

Если модуль перемещения тела
много меньше расстояния до центра Земли, то можно считать силу всемирного
тяготения во время движения постоянной, а движение тела равноускоренным. Самый
простой случай движения тела под действием силы тяжести — свободное падение с
нулевой начальной скоростью. В этом случае тело движется с ускорением
свободного падения к центру Земли. Если есть начальная скорость, направленная
не по вертикали, то тело движется по криволинейной траектории (параболе, если
не учитывать сопротивление воздуха).

При некоторой начальной скорости
тело, брошенное по касательной к поверхности Земли, под действием силы тяжести
при отсутствии атмосферы может двигаться по окружности вокруг Земли, не падая
на нее и не удаляясь от нее. Такая скорость называется первой космической
скоростью, а тело, движущееся таким образом — искусственным спутником
Земли (ИСЗ).

Определим первую космическую
скорость для Земли. Если тело под действием силы тяжести движется вокруг Земли
равномерно по окружности, то ускорение свободного падения является его
центростремительным ускорением:

Отсюда первая космическая скорость
равна

Первая космическая скорость для
любого небесного тела определяется таким же образом. Ускорение свободного
падения на расстоянии R от
центра небесного тела можно найти, воспользовавшись вторым законом Ньютона и
законом всемирного тяготения:

Следовательно, первая
космическая скорость на расстоянии R от
центра небесного тела массой M равна

Для запуска на околоземную
орбиту ИСЗ необходимо сначала вывести за пределы атмосферы. Поэтому космические
корабли стартуют вертикально. На высоте 200 — 300 км от поверхности Земли, где
атмосфера разрежена и почти не влияет на движение ИСЗ, ракета делает поворот и
сообщает ИСЗ первую космическую скорость в направлении, перпендикулярном
вертикали.

Равномерное движение по окружности

При равномерном движении по
окружности значение скорости постоянно, а ее направление изменяется в процессе
движения. Мгновенная скорость тела всегда направлена по касательной к
траектории движения.

Т. к. направление скорости при
равномерном движении по окружности постоянно изменяется, то это движение всегда
равноускоренное.

Промежуток времени, за который
тело совершает полный оборот при движении по окружности, называется периодом:

Т. к. длина окружности s равна 2pR, период обращения при равномерном движении тела со
скоростью v по окружности радиусом R
равен:

Величина, обратная периоду
обращения, называется частотой обращения и показывает, сколько оборотов по
окружности совершает тело в единицу времени:

Угловой скоростью называется
отношение угла, на который повернулось тело, к времени поворота:

Угловая скорость численно равна
числу оборотов за 2p секунд. Ускорение
при равномерном движении тел по окружности (центростремительное ускорение). При
равномерном движении по окружности тело движется с центростремительным
ускорением. Определим это ускорение.

Ускорение направлено туда же,
куда и изменение скорости, следовательно, ускорение направлено к центру
окружности

Важное допущение: угол j
настолько мал, что длина хорды AB совпадает с длиной
дуги:

по
двум пропорциональным сторонам и углу между ними. Следовательно:

— модуль центростремительного
ускорения.

Распространение на протяжённые тела[]

Классическая механика также включает в себя описание сложных движений протяжённых неточечных объектов. Распространение законов ньютоновой механики на такие объектов было в основном заслугой Эйлера. Современная формулировка законов Эйлера также использует аппарат трёхмерных векторов.

Позднее развивается аналитическая механика, основная идея которой — описание механической системы как единого объекта, использующее аппарат многомерной геометрии. Есть две основные (во многом альтернативные) формулировки классической аналитической механики: лагранжева механика и гамильтонова механика. В этих теориях понятие «сила» во многом отходит на второй план, а упор при описании механических систем делается на другие физические величины — такие, как энергия или действие.

Приведенные выше выражения для импульса и кинетической энергии действительны только при отсутствии значительного электромагнитного вклада. В электромагнетизме второй закон Ньютона для провода с током нарушается, если не учитывать вклад электромагнитного поля в импульс системы; такой вклад выражается через вектор Пойнтинга, поделённый на c2, где c — это скорость света в свободном пространстве.

История[]

Древнее время

Классическая механика зародилась в древности главным образом в связи с проблемами, которые возникали при строительстве. Первым из разделов механики, получившим развитие, стала статика, основы которой были заложены в работах Архимеда в III веке до н. э. Им были сформулированы правило рычага, теорема о сложении параллельных сил, введено понятие центра тяжести, заложены основы гидростатики (сила Архимеда).

Средние века

В XIV веке французский философ Жан Буридан разработал теорию импетуса. В дальнейшем её развил ученик Жана — епископ Альберт Саксонский.

Новое время

XVII век

Динамика как раздел классической механики начал развиваться только в XVII веке. Его основы были заложены Галилео Галилеем, который первым правильно решил задачу о движении тела под действием заданной силы. На основе эмпирических наблюдений им были открыты закон инерции и принцип относительности. Помимо этого, Галилеем внесён вклад в зарождение теории колебаний и науки о сопротивлении материалов.

Христиан Гюйгенс проводил исследования в области теории колебаний, в частности изучал движение точки по окружности, а также колебания физического маятника. В его работах были также впервые сформулированы законы упругого удара тел.

Заложение основ классической механики завершилось работами Исаака Ньютона, сформулировавшего в наиболее общей форме законы механики и открывшего закон всемирного тяготения. Им же в 1684 году был установлен закон вязкого трения в жидкостях и газах.

Также в XVII веке в 1660 году был сформулирован закон упругих деформаций, носящий имя своего первооткрывателя Роберта Гука.

XVIII век

В XVIII веке зарождается и интенсивно развивается аналитическая механика. Её методы для задачи о движении материальной точки были разработаны Леонардом Эйлером, которые заложил основы динамики твёрдого тела. Эти методы основываются на принципе виртуальных перемещений и на принципе Д’Аламбера. Разработку аналитических методов завершил Лагранж, которому удалось сформулировать уравнения динамики механической системы в наиболее общем виде: с использованием обобщённых координат и импульсов. Помимо этого, Лагранж принял участие в заложении основ современной теории колебаний.

Альтернативный метод аналитической формулировки классической механики основывается на принципе наименьшего действия, который впервые был высказан Мопертюи по отношению к одной материальной точке и обобщён на случай системы материальных точек Лагранжем.

Также в XVIII веке в работах Эйлера, Даниила Бернулли, Лагранжа и Д’Аламбера были разработаны основы теоретического описания гидродинамики идеальной жидкости.

XIX век

В XIX веке развитие аналитической механики происходит в работах Остроградского, Гамильтона, Якоби, Герца и др. В теории колебаний Раусом, Жуковским и Ляпуновым была разработана теория устойчивости механических систем. Кориолис] разработал теорию относительного движения, доказав теорему о разложении ускорения на составляющие. Во второй трети XIX века происходит выделение кинематики в отдельный раздел механики (хотя впервые мысль о целесообразности такого выделении кинематики была высказана ещё Эйлером в 1776 г.).

Особенно значительны в XIX веке были успехи в области механики сплошной среды. Навье и Коши в общей форме сформулировали уравнения теории упругости. В работах Навье и Стокса были получены дифференциальные уравнения гидродинамики с учётом вязкости жидкости. Наряду с этим происходит углубление знаний в области гидродинамики идеальной жидкости: появляются работы Гельмгольца о вихрях, Кирхгофа, Жуковского и Рейнольдса о турбулентности, Прандтля о пограничных эффектах. Сен-Венан разработал математическую модель, описывающую пластические свойства металлов.

В XX веке интерес исследователей переключается на нелинейные эффекты в области классической механики. Ляпунов и Анри Пуанкаре заложили основы теории нелинейных колебаний. Мещерский и Циолковский провели анализ динамики тел переменной массы. Из механики сплошной среды выделяется аэродинамика, основы которой разработаны Жуковским. В середине XX века активно развивается новое направление в классической механике — теория хаоса. Важными также остаются вопросы устойчивости сложных динамических систем.

Ускорение

Ускорением называется
векторная физическая величина, равная отношению очень малого изменения вектора
скорости к малому промежутку времени, за которое произошло это изменение, т.е.
это мера быстроты изменения скорости:

;
.

Метр в секунду за секунду — это
такое ускорение, при котором скорость тела, движущегося прямолинейно и
равноускоренно, за время 1 с изменяется на 1 м/с.

Направление вектора ускорения
совпадает с направлением вектора изменения скорости () при очень малых значениях промежутка
времени, за который происходит изменение скорости.

Если тело движется по прямой и
его скорость возрастает, то направление вектора ускорения совпадает с
направлением вектора скорости; при убывании скорости — противоположно
направлению вектора скорости.

При движении по криволинейной
траектории направление вектора скорости изменяется в процессе движения, вектор
ускорения при этом может оказаться направлен под любым углом к вектору
скорости.

Правила параллелограмма в механике

Рисунок 2. Формулы по механике. Автор24 — интернет-биржа студенческих работ

Из трех фундаментальных теорий движения тела Ньютона вытекают определенные следствия, одно из которых — сложение общего количества элементов по правилу параллелограмма. Согласно данной идее, ускорение любого физического вещества зависит от величин, в основном характеризующих действие иных тел, определяющих особенности самого процесса. Механическое действие на исследуемый объект со стороны внешней среды, которая кардинально изменяет скорость движения сразу нескольких элементов, называют силой. Она может иметь многогранную природу.

В классической механике, которая имеет дело со скоростями, значительно меньшими скорости света, масса считается одной из основных характеристик самого тела, не зависящей от того, движется оно или находится в состоянии покоя. Масса физического тела находится вне зависимости от взаимодействия вещества с другими частями системы.

Замечание 1

Таким образом, масса стала постепенно пониматься как количество живой материи.

Установление понятий массы и силы, а также метода их измерения позволило Ньютону описать и сформулировать второй закон классической механики. Итак, масса есть одна из ключевых характеристик материи, определяющая ее гравитационные и инертные свойства.

Первое и второе начало механики относятся соответственно к систематическому движению одного тела или материальной точки. При этом учитывается только действие других элементов в определенной концепции. Однако любое физическое действие есть взаимодействие.

Третий закон механики уже фиксирует данное утверждение и гласит: действию всегда соответствует противоположно направленное и равное противодействие. В формулировке Ньютона этот постулат механики справедлив лишь для случая непосредственной взаимосвязи сил или при внезапной передаче действия одного материального тела на другое. В случае перемещения за длительный промежуток времени третий закон применяется тогда, когда временем передачи действия возможно пренебречь.

Вообще все законы классической механики справедливы для функционирования инерциальных систем отсчета. В случае неинерциальных концепций ситуация совершенно иная. При ускоренном движении координат относительно самой инерциальной системы первый закон Ньютона невозможно использовать — свободные тела в ней будут менять свою скорость движения с течением времени и зависеть от скорости движения и энергии других веществ.

Первый закон механики

Некоторое время в физике никто не подвергал сомнению мысль Аристотеля, высказанную им в работе «Механика»: «Движущееся тело останавливается, если сила, толкающая его, прекращает свое действие».

Это ошибочное утверждение, опирающееся на обыденное восприятие явлений природы, впервые опроверг Галилей, сделавший важнейший для науки вывод о вечности, неуничтожаемости движения.

Анализируя движение шарика по наклонной плоскости (рис. 2.1), он писал: «…скорость, которую однажды сообщили телу, будет строго сохранятся, поскольку устранены внешние причины ускорения и замедления, — условие, которое обнаруживается только на горизонтальной плоскости, ибо в случае движения по наклонной плоскости вниз уже существует причина ускорения, в то время как при движении по наклонной плоскости вверх налицо замедление; из этого следует, что движение по горизонтальной плоскости вечно, ибо, если скорость будет постоянной, движение не может быть уменьшено или ослаблено, а тем более уничтожено».

Этот фундаментальный вывод Г. Галилея использовал И. Ньютон в своем знаменитом труде «Математические начала натуральной философии» (1687 г.) при формулировании первого закона динамики (закона инерции):

Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, поскольку оно не принуждается приложенными силами изменить это состояние.

А. Эйнштейн и Л. Инфельд в работе «Эволюция физики» проще сформулировали этот закон: «Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, если только оно не вынуждено изменить его под влиянием действующих сил».

Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.

Движение шарика по наклонной плоскости рассматривали относительно поверхности Земли, которая считалась неподвижной. Итак, первый закон динамики установлен для систем отсчета, считающихся неподвижными или движущихся относительно последних прямолинейно, равномерно и поступательно. Такие системы называются инерциальными. Инертность тел проявляется в сохранении ими своего состояния покоя или прямолинейного равномерного движения до того времени, пока какая-нибудь внешняя причина не выведет их из этого состояния.

Тело большой массы сложнее разогнать до некоторой скоро сти, чем тело малой массы, так как оно более инертно.

Сущность инертности, которая свойственна всем телам, заключается в том, что для изменения скорости тела необходимо взаимодействие с другим телом. Из двух взаимодействующих тел более инертно то, которое медленнее изменяет свою скорость.

Теоретически инерциальных систем отсчета может быть много, поскольку всегда можно представить тела, которые пребывают в состоянии покоя или движутся равномерно и прямолинейно (без ускорения), и связать с ними соответствующее количество систем координат и устройств для отсчета времени (часов).

Понятие инерциальной системы отсчета является научной абстракцией. В реальной жизни таких систем нет, поскольку в природе не существует абсолютно неподвижных тел (например, тело, которое неподвижно относительно Земли, вращается вместе с ней вокруг земной оси, вокруг Солнца и т. д.).

При решении задач динамики систему отсчета связывают с реальным телом, например Землей или Солнцем.

Поэтому при решении задач динамики систему отсчета связывают с реальным телом. Тогда она может рассматриваться как инерциальная с той или иной степенью приближения.

Так, например, при решении задач в небесной механике и космонавтике с высокой степенью точности инерциальной можно считать гелиоцентрическую систему с началом отсчета на Солнце и осями, направленными на некоторые звезды. Для решения большинства технических задач в качестве инерциальной берут систему отсчета, жестко связанную с Землей.

Сила. Масса. Динамометр

Вспомним основные понятия, которые используются в механике.

Сила

Силой в физике принято считать количественную меру воздействия одного тела, на другое. В результате этого воздействия тела ускоряются (замедляются) или же деформируются.

Важно понимать, что понятие «сила» относится обязательно к двум телам: тому, на которое оказывается воздействие; тому, которое оказывает воздействие. Всегда важно узнавать со стороны какого тела действует сила и на какое

Существуют силы различной природы – силы трения, гравитационные, электрические и так далее. Подробно они будут рассматриваться в дальнейшем курсе физики.

Динамометр

Для измерения силы используется прибор, названный динамометром. Схема динамометра и сам динамометр изображены на рисунке 1. Итак, этот прибор состоит из пружинки, которая растягивается при воздействии на нее силы и шкалы, на которой эта пружинка закреплена. Деформация пружинки прямо пропорциональна силе, с которой на эту пружинку действуют (например, когда к крючку внизу шкалы подвешивают грузик).

Подробнее принцип действия этого прибора будет рассматриваться при изучении сил упругости и закона Гука.

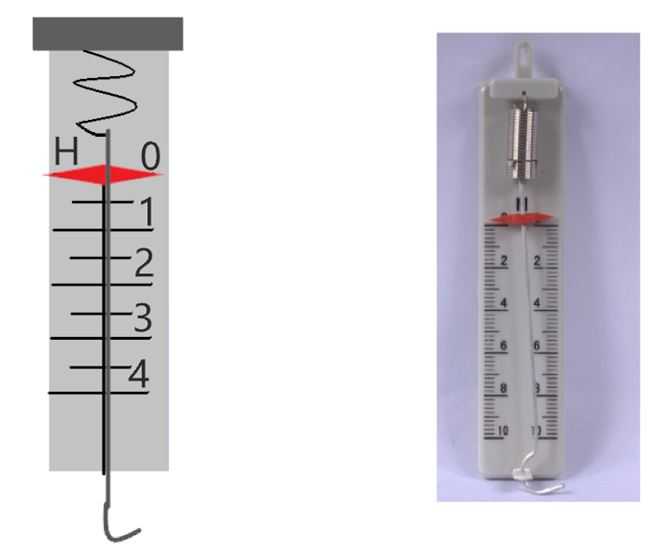
Рисунок 1 – Динамометр

Масса

Из практического опыта всем известно, что различные тела при воздействии на них силой по-разному меняют свою скорость: например, надувной мяч легко сдвигается с места от легкого пинка ногой, а, чтобы переместить булыжник, необходимо приложить значительно больше усилий.

Способность тела противиться изменению своей скорости называют инертностью. А количественной мерой инертности, как физической величины, принята масса (m).

Масса тела – скалярная величина. Единицей измерения массы в СИ являются килограммы (кг). Но также можно использовать и граммы, тонны и другие единицы.

m] = кг.