Вынужденные колебания в физике - формулы и определения с примерами

Что такое автоколебательные системы

Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.

Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.

Рисунок 2 . 5 . 4 . Автоколебательная система со всеми основными составляющими.

Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.

Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.

Рисунок 2 . 5 . 5 . Схема маятникового часового механизма.

Резонанс — что это в физике простыми словами

В переводе с латинского слово «резонанс» буквально означает «откликаюсь». Он представляет собой физическое явление, при котором собственное колебательное движение становится вынужденным, постоянно увеличивая свою амплитуду из-за воздействия окружающей среды.

Резонанс можно описать следующим образом:

представьте, что определенное физическое тело находится в состоянии абсолютного покоя или совершает движения с определенной амплитудой и частотой;
на это тело внезапно воздействует внешняя сила, имеющая свою собственную амплитуду и частоту;
если частоты тела и внешние силы совпадают, то амплитуда тела будет расти.

Например, все знают, как работает «качели». Сначала вы поднимаете ноги над землей, а затем качели начинают двигаться вперед и назад. Если вы прекратите движение ногами и телом, качели через некоторое время остановятся.

Даже малые внешние воздействия могут увеличить скорость движения этой системы несколько раз при совпадении частот. Если же частота системы и внешних сил не совпадает, то речь идет о диссонансе.

Слово «диссонанс» означает «несоответствие и непоследовательность».

Возьмем к примеру качели: если вы дергаете их в произвольном направлении или противоположно их ходу, то движение качелей скоро прекратится.

Опасность и польза явления

На первый взгляд, резонанс — полезное явление, которое помогает нам в различных аспектах жизни. Например, он успешно используется, когда автомобиль застрял колесами в грязи или снегу, и не может двигаться. Раскачивание автомобиля назад и вперед помогает выехать.

Но это физическое явление имеет и негативную сторону. У архитекторов есть термин «Такомский мост»: название объекта, при строительстве которого не был учтен эффект вынужденного механического резонанса. В результате центральный пролет моста был разрушен 7 ноября 1940 года при силе ветра около 65 км/ч, который и стал причиной резонанса. Ветер усилил колебания конструкции, что привело к трагедии. После этого инцидента технологии строительства мостов кардинально изменились.

Известен еще один печальный случай с мостом, который рухнул, когда по нему шел отряд солдат. Солдаты маршировали в ногу, создавая мощную вибрацию, совпадающую с вибрацией конструкции, и тем самым раскачивая его. С тех пор появилась новая команда «не в ногу!», которой командиры пользуются до сих пор, когда большая группа солдат пересекает висячий мост.

Явление резонанса также необходимо учитывать в строительных блоках, антеннах, высотных опорах — во всем, что может войти в резонанс воздушным потоком.

Виды и примеры резонанса

Явление резонанса связано с физикой, так как оно было открыто и первоначально описывало только физические явления.

В этом отношении можно выделить различные виды:

Механические — вышеупомянутые качели, звон «языкового» колокола, резонанс моста от проходящего поезда или солдат, идущих по нему «в ногу» и т.д.
Акустический — примером может быть использование акустического резонанса, используемого для игры на музыкальных инструментах (например: гитаре, балалайке, домре). Звук струны отражается от тела музыкального инструмента эхом, который приводит к его усилению. Таким образом, качество звучания напрямую зависят от качества материала, из которого изготавливается инструмент.
Частота электрического совпадения внешнего напряжения с частотой собственных колебаний в электрической цепи, по которой протекает ток.
Общественность — четкая реакция общественности на событие или ситуацию. Речь идет о реакции, которая оказалась похожей у большинства людей. Например, пенсионная реформа 2018 года вызвала громкий, резкий и негативный резонанс среди граждан России.
Когнитивный резонанс — совпадение мнений и взглядов. Например, при знакомстве с человеком возникло позитивное впечатление о нем. Почему? Скорее всего, в разговоре вы нашли много общего с ним, его ценности и мысли были близки, так что симпатия была вызвано резонансом (совпадением). В философском термине это явление означает единство двух душ в чувственной среде.

Сотовые телефоны, микроволновая печь, телевизор, горное эхо, звонкое пение в ванной — явление резонанса присутствует повсюду.

Длина волны

Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах. Обозначение – $ \lambda $ , единицы измерения – м.

Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.

Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

наличие источника звука;
наличие упругой среды между источником и приемником звука;
наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

инфразвук ( $ \nu $ $ \nu $ $ \nu $ > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны. Шум – хаотическая смесь тонов.

Изображение и описание

Самым наглядным способом отображения колебаний является график функций, описывающий изменение. Для поддержания периодичности нужна внешняя сила. Подчиняется она различным законам. В простейшем случае правило имеет гармонический вид. Например, изменение силы можно описать функцией: f = F0 * cos (wt).

Чтобы составить уравнение движение, кроме вынуждающего действия, нужно учитывать 2 другие силы: квазиупругую и сопротивления. Первая направлена к центру и пропорциональна расстоянию от середины до места приложения: F = c * r, где c — постоянная составляющая. При этом тело получает потенциальную энергию: Ep = 1 / (2 *c * r2). Вторая же характеризуется физической плотностью среды, где происходит колебание.

Если принять отклонения от равновесия за небольшое, сила сопротивления будет прямо пропорциональна скорости. Уравнение можно переписать: mx = -kx — rx + F0 * cos (wt). Сократив обе части равенства на cx, можно получить неоднородное уравнение линейного вида: x + 2bx + w2x = f*cos (wt), где f = F/m — частота; b = r/2m — коэффициент затухания; w = √‎(k/m) — частота колебаний. Решение равенства будет иметь вид: x = a*cos (wt — φ).

Изобразить гармоническое колебание, описываемое по формуле x (T) = A * cos (wt+φ) удобно, используя векторную диаграмму. Для этого нужно выполнить следующее:

Построить ось игрек и икс.
Изобразить вектор, длина которого будет равняться A. При этом он должен образовывать с осью икс угол фи.
Положительный угол отложить против движения часовой стрелки.
Определить проекции вектора на оси абсциссы и ординаты. Ими будут функции: y = A * sin (φ) и x = A * cos (φ).

Вращение вектора определяется двумя функциями: y (t) = A * sin (wt*φ) и x (t) = A * cos (wt + φ). Вынужденное колебание можно представить в виде изменения проекции на координатные линии некого вектора A. Причём модуль равняется амплитуде и вращается со скоростью φ, образуя в исходный момент времени с осью игреков φ0.

Суть явления резонанса

Резонанс в физике – это частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы.

Известны случаи, когда мост, по которому маршировали солдаты, входил в резонанс от строевого шага, раскачивался и разрушался. Кстати, именно поэтому сейчас при переходе через мост солдатам положено идти вольным шагом, а не в ногу.

Египетский мост в Санкт-Петербурге, разрушившийся из-за резонанса.

Уравнение вынужденных колебаний

Вынужденными колебаниями называют периодические изменения параметров, которые описывают систему под влиянием внешней силы. Для реализации вынужденных электрических колебаний в $RLC$ контуре в него включают переменную ЭДС (рис.1).

Рисунок 1.

В общем случае вынужденные колебания в таком контуре можно записать как:

где $L$ — индуктивность, $R$ — сопротивление, $C$ — емкость, $U\left(t\right)$ — внешнее воздействие.

Рассмотрим случай, когда в контур подается переменное напряжение ($U$) изменяющееся по гармоническому закону:

Тогда уравнение колебаний запишется в виде:

где ${\omega }_0=\frac{1}{\sqrt{LC}}$- собственная частота колебаний контура, $\beta =\frac{R}{2L}.$ По аналогии с механическими колебаниями можно записать частное решение данного уравнения как:

где $q_m=\frac{U_m}{\omega \sqrt{{R^2+\left(\omega L-1/\omega C\right)}^2}},\ tg\Psi=\frac{R}{\frac{1}{\omega C}-\omega L}$.

Как известно, общее решение неоднородного уравнения получают как сумму частного решения данного уравнения (в нашем случае это (4)) и общего решения соответствующего однородного уравнения. Так для уравнения:

общим решением является выражение:

Так как выражение (6) содержит множитель $e^{\left(-\beta t\right)}$, то при $t\to \infty ,\ $ $e^{\left(-\beta t\right)}\to 0,$ поэтому для установившихся колебаний решением уравнения (3) считают функцию (4).

Сила тока для установившихся вынужденных колебаний может быть записана как:

где $I_m={\omega q}_m$, $\varphi =\Psi-\frac{\pi }{2}$ — сдвиг фаз между тока и приложенного напряжения. Соответственно:

Надо отметить, что выполняется равенство:

Выражение (9) означает, что сумма напряжений на каждом из элементов цепи в момент времени $t$ равна приложенному напряжению.

Примеры резонанса

Явление резонанса наблюдается в самых разных физических процессах. Например, звуковой резонанс. Возьмём гитару. Само по себе звучание струн гитары будет тихим и почти неслышным. Однако струны неспроста устанавливают над корпусом – резонатором. Попав внутрь корпуса, звук от колебаний струны усиливается, а тот, кто держит гитару, может почувствовать, как она начинает слегка «трястись», вибрировать от ударов по струнам. Иными словами, резонировать.

Еще один пример наблюдения резонанса, с которым мы сталкиваемся — круги на воде. Если кинуть в воду два камня, попутные волны от них встретятся и увеличатся.

Действие микроволновки также основано на резонансе. В данном случае резонанс происходит в молекулах воды, которые поглощают излучение СВЧ (2,450 ГГц). Как следствие, молекулы входят в резонанс, колеблются сильнее, а температура пищи повышается.

Резонатор гитары

Резонанс может быть как полезным, так и приносящим вред явлением. А прочтение статьи, как и помощь нашего студенческого сервиса в трудных учебных ситуациях, принесет вам только пользу. Если в ходе выполнения курсовой вам понадобится разобраться с физикой магнитного резонанса, можете смело обращаться в нашу компанию за быстрой и квалифицированной помощью.

Напоследок предлагаем посмотреть видео на тему «резонанс» и убедиться в том, что наука может быть увлекательной и интересной. Наш сервис поможет с любой работой: от реферата до курсовой по физике колебаний или эссе по литературе.

Явление резонанса

При колебаниях может наступить момент приближения частоты вынуждающего воздействия к собственной частоте движения системы. В этом случае физики говорят, что установился резонанс. Другими словами, происходит амплитудное возрастание вынужденных колебаний при равенстве циклической частоты, которую называют резонансной. На графике зависимостей A от w кривая, описывающая явление, имеет наибольшую величину.

Амплитуду можно вычислить по формуле: A = F/2 gm √(‎ w2 — g), где g — коэффициент затухания, то есть чем больше g, тем более будет сдвинут максимум к нулевой отметке на графике. Лучше проявляется резонанс в системах, характеризующихся малым затуханием. В ином случае циклическая частота будет мнимой, а амплитуда — монотонно уменьшаться.

Описывать колебательную систему можно через добротность (Q). Эта величина определяется из отношения энергии, которую удалось накопить, к значению её расхода за один период. С помощью этого параметра определяют качество, так как чем добротность больше, тем меньше система теряет энергию. Для любого механического периодичного движения её можно вычислить так: Q = √ (m * k) / r = (w * m) / r, где: m — масса системы, k — жёсткость, r — сопротивление.

При помощи явления можно выделить или даже усилить довольно слабые периодические колебания. В радиотехнике его используют для получения полезного сигнала, усиления звука. Что интересно, впервые о резонансе заговорил Галилео Галилей в 1602 году, исследуя движения маятников и музыкальных струн. Он предположил, что резонанс — это отклик на силу извне, при котором происходит синхронизация частот колебаний с воздействующей на неё внешней силы. Это явление приводит к росту амплитуды движения всей системы.

Механические колебания. Свободные и вынужденные колебания. Резонанс. Превращение энергии …

Механические колебания – это движения, которые точно или приблизительно повторяются через определенные интервалы времени. (например, колебание ветки на дереве, маятника часов, автомобиля на рессорах и так далее)

Колебания бывают свободными и вынужденными.

Колебания, возникающие в системе под действием внутренних сил, называются свободными . Все свободные колебания затухают. (например: колебание струны, после удара)

Колебания, совершаемые телами под действием внешних периодически изменяющихся сил, называются вынужденными (например: колебание металлической заготовки при работе кузнеца молотом).

Условия возникновения свободных колебаний :

При выведении тела из положения равновесия в системе должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
Силы трения в системе должны быть очень малы (т.е. стремиться к нулю).

В реальных колебательных системах всегда происходят потери энергии при свободных колебаниях. Механическая энергия расходуется на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, затем колебания прекращаются. Колебания, энергия которых уменьшается с течением времени за счет действия сил сопротивления, называются затухающими.

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Любое колебание характеризуется:

X_m (А)– модуль максимального смещения точки от положения равновесия называется амплитудой (м);
T – время одного полного колебания называется периодом (с);
Число колебаний в единицу времени называется частотой (ν):

Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний ().

Явление резонанса учитывается в акустике, радиотехнике и технике. В строительстве, например, при сооружении мостов и других сооружений, которые подвержены механическим колебаниям и действию внешней силы.

Существует несколько колебательных систем – математический маятник (шарик на тонкой длинной нити) и пружинный маятник (тело на пружине).

Самый простой вид колебательного движения — гармонические колебания, при которых физическая величина периодически изменяется со временем по закону синуса или косинуса (рис.).При гармонических колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно :

… Е_кин → Е_р → Е_кин →…

На примере колебаний тела на нити видим превращение энергии. В 1 положении наблюдаем равновесие колебательной системы. Скорость и, следовательно, кинетическая энергия тела максимальны. При отклонении маятника от положения равновесия он поднимается на высоту h относительно нулевого уровня, следовательно, в точке А маятник обладает потенциальной энергией Е_р. При движении к положению равновесия, к точке О, уменьшается высота до нуля, а скорость груза увеличивается, и в точке О вся потенциальная энергия Е_р превратится в кинетическую энергию Е_кин. В положении равновесия кинетическая энергия имеет максимальное значение, а потенциальная энергия минимальна. После прохождения положения равновесия по инерции происходит превращение кинетической энергии в потенциальную, скорость маятника уменьшается и при максимальном отклонении от положения равновесия становится равной нулю. Е_кин= 0, Е_р = max

Закон сохранения механической энергии: сумма кинетической и потенциальной энергий остается неизменной: Е_кин = Е_р = const

Свободные колебания (математический и пружинный маятники)

Свободные колебания – колебания, которые совершает тело под действием внутренних сил системы за счет начального запаса энергии после того как его вывели из положения устойчивого равновесия.

Условия возникновения свободных колебаний:

при выведении тела из положения равновесия должна возникнуть сила, стремящаяся вернуть его в положение равновесия;
силы трения в системе должны быть достаточно малы. При наличии сил трения свободные колебания будут затухающими.

При наличии сил трения свободные колебания будут затухающими. Затухающие колебания – это колебания, амплитуда которых с течением времени уменьшается.

Математический маятник – это материальная точка, подвешенная на невесомой нерастяжимой нити.

Период колебаний математического маятника:

Частота колебаний математического маятника:

Циклическая частота колебаний математического маятника:

Максимальное значение скорости колебаний математического маятника:

Максимальное значение ускорения колебаний математического маятника:

Период свободных колебаний математического маятника, движущегося вверх с ускорением или вниз с замедлением:

Период свободных колебаний математического маятника, движущегося вниз с ускорением или вверх с замедлением:

Период свободных колебаний математического маятника, горизонтально с ускорением или замедлением:

Мгновенное значение потенциальной энергии математического маятника, поднявшегося в процессе колебаний на высоту $ h $ , определяется по формуле:

где $ l $ – длина нити, $ \alpha $ – угол отклонения от вертикали.

Пружинный маятник – это тело, подвешенное на пружине и совершающее колебания вдоль вертикальной или горизонтальной оси под действием силы упругости пружины.

Период колебаний пружинного маятника:

Частота колебаний пружинного маятника:

Циклическая частота колебаний пружинного маятника:

Максимальное значение скорости колебаний пружинного маятника:

Максимальное значение ускорения колебаний пружинного маятника:

Мгновенную потенциальную энергию пружинного маятника можно найти по формуле:

Амплитуда потенциальной энергии – максимальное значение потенциальной энергии, величина, стоящая перед знаком синуса или косинуса:

Важно! Если маятник не является ни пружинным, ни математическим (физический маятник), то его циклическую частоту, период и частоту колебаний по формулам, применимым к математическому и пружинному маятнику, рассчитать нельзя. В данном случае эти величины рассчитываются из формулы силы, действующей на маятник, или из формул энергий

Вынужденные колебания. Резонанс

Подробности: Обновлено 21.07.2018 11:44; Просмотров: 754

«Физика — 11 класс»

Как получить незатухающие колебания, — те, которые могут длиться неограниченно долго?

Для этого на колебателььную систему должна действовать внешняя периодическая сила.
Такие колебания называются вынужденными.

Работа внешней силы над системой обеспечивает приток энергии к системе извне, который не дает колебаниям затухнуть, несмотря на действие сил трения.

Например, раскачивание ребенка на качелях.
Качели — это маятник, т. е. колебательная система с определенной собственной частотой.
Если начать в правильном ритме подталкивать качели, то можно без большого напряжения раскачать их очень сильно.
При этом произойдет накопление результатов действия отдельных толчков, и амплитуда колебаний качелей станет большой.

В этом случае возникает возможность увеличения амплитуды колебаний системы, способной совершать почти свободные колебания, при совпадении частоты внешней периодической силы с собственной частотой колебательной системы.

Спустя некоторое время колебания качелей приобретут установившийся характер: их амплитуда перестанет изменяться со временем.

При установившихся вынужденных колебаниях частота колебаний всегда равна частоте внешней периодически действующей силы.

Резонанс

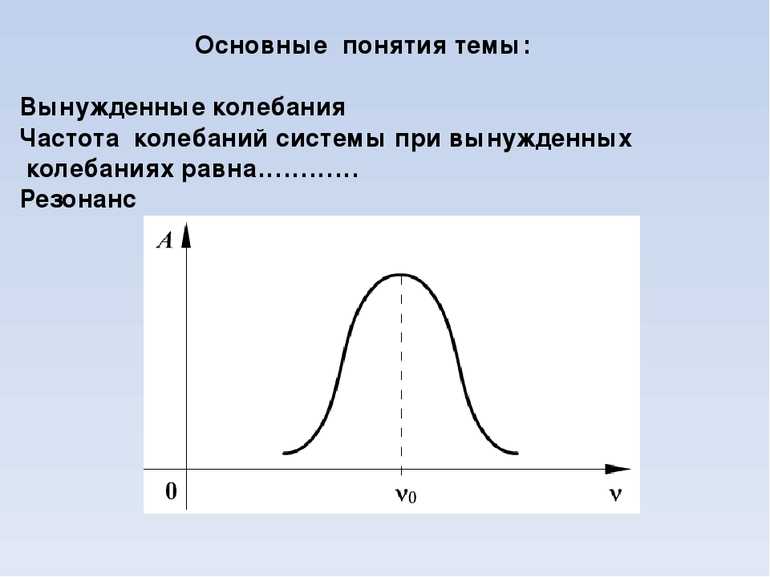
Как амплитуда установившихся вынужденных колебаний зависит от частоты внешней силы?
При увеличении частоты внешней силы амплитуда колебаний постепенно возрастает.
Она достигает максимума, когда частота вынужденных колебаний становится равной частоте внешней периодически действующей силы.
При дальнейшем увеличении частоты амплитуда установившихся колебаний уменьшается.

Резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой ее свободных колебаний называется резонансом.

Почему возникает резонанс?

При резонансе внешняя сила действует в такт со свободными колебаниями.
Ее направление совпадает с направлением скорости мммаятника, поэтому эта сила совершает только положительную работу.
При установившихся колебаниях положительная работа внешней силы равна по модулю отрицательной работе силы сопротивления.

Большое влияние на резонанс оказывает трение в системе.
Чем меньше коэффициент трения, тем больше амплитуда установившихся колебаний.

Изменение амплитуды вынужденных колебаний в зависимости от трения:

кривая 1 — минимальное трение,
кривая 3 — максимальное трение.
Возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе.
При малом трении резонанс «острый», а при большом «тупой».

Согласно закону сохранения энергии вызвать в системе колебания с большой амплитудой при небольшой внешней силе можно только за продолжительное время.
Если трение велико, то амплитуда колебаний будет небольшой, и для установления колебаний не потребуется много времени.

Воздействие резонанса и борьба с ним

Если колебательная система находится под действием внешней периодической силы, и если частота этих периодических усилий совпадает с частотой свободных колебаний системы, то может наступить резонанс и резкое увеличение амплитуды колебаний.

Любое упругое тело, будь то мост, вал двигателя, корпус корабля, представляет собой колебательную систему и характеризуется собственными частотами колебаний.
В то же время железо, сталь и другие материалы при переменных нагрузках со временем теряют прочность, после чего внезапно разрушаются.
Обычно принимаются специальные меры, чтобы не допустить наступления резонанса или ослабить его действие.

Для этого увеличивают трение или же добиваются, чтобы собственные частоты колебаний не совпадали с частотой внешней силы.
Известны случаи, когда приходилось перестраивать океанские лайнеры, чтобы уменьшить вибрацию.
Или при переходе через мост воинским частям запрещается идти в ногу, т.к. строевой шаг приводит к периодическому воздействию на мост.

Следующая страница «Кратко о механических колебаниях»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные, затухающие и вынужденные колебания —
Условия возникновения свободных колебаний. Математический маятник —
Динамика колебательного движения. Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы