Гармонические колебания — характеристика, закон и формулы

Трактовка понятий

Чтобы записать закон гармонических колебаний математическим способом, используются следующие формулы: х (t)= A sin (wt+f) и х (t)= A cos (wt+f). Через x вычисляется изменяющаяся величина. Для времени используется t. Трактовка остальных постоянных параметров:

• А — амплитуда колебаний (АК);
• w — циклическая частота колебаний (ЦЧК);
• (wt+f) — полная фаза;
• f — начальный период.

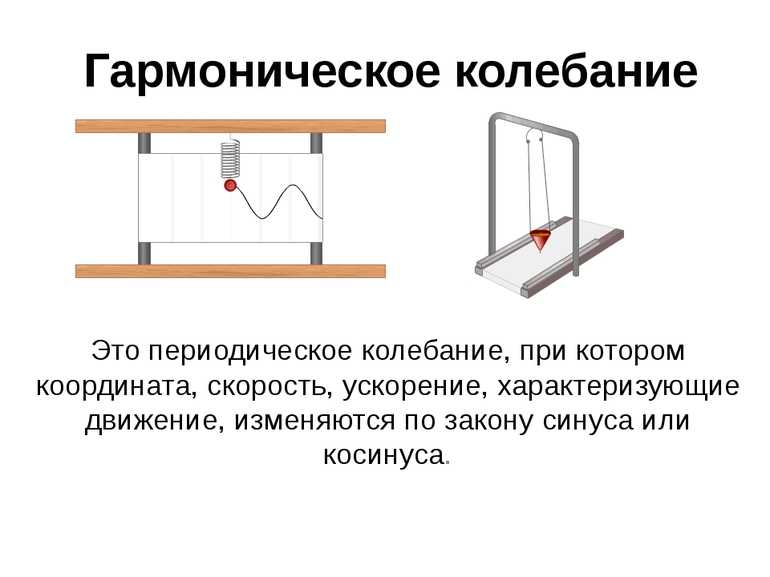
В дифференциальном виде уравнение гармонических колебаний записывается следующим образом: d²x/dt²+w²x=0. Нетривиальное решение такого примера — гармоническое колебание (ГК) с зависимостью от величины w. Если точка двигается по окружности равномерно, тогда любая её проекция на прямую будет лежать в этой плоскости. Условия, при которых могут происходить изменения, — воздействие силы тяготения небольшого груза, подвешенного на длинной нити. На практических занятиях по физике ученики используют маятник. Вместо нити может применяться пружина либо иное тело.

Для него характерны малые амплитуды. ГК под воздействием силы упругости способствует изменению состояния пружины. Аналогичные движения совершает балансир в механических часах. Если рассматривать материальную точку, она выполняет КГ в положении равновесия. При периодических колебаниях (ПК) движение характеризуется координатой.

https://youtube.com/watch?v=ke237hiv304

Что такое гармонические колебания в физике

Гармонические колебания и их характеристики изучает отдельный раздел физики. Основу данных процессов составляет величина, изменяемая в течение определенного временного интервала (периода), согласно косинусоидальному или синусоидальному (гармоническому) закону.

В течение одного периода тело может совершать различные движения:

• смещаться;
• вращаться;
• свободно ускоряться.

Данные изменения отражает график. Они могут быть:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

• механическими;
• электромагнитными;
• электромеханическими.

Гармонические колебания являются такими колебаниями, при которых характеристики движения в виде координаты, скорости и ускорения изменяются, согласно закону синуса или косинуса.

Колебания представляют собой процессы, которые обладают индивидуальными особенностями в зависимости от степени повторяемости. В качестве примера можно привести качели, ветку дерева, фазы луны, морские приливы и отливы, пульсовые волны, сердце, гортань. В технике и окружающем мире часто можно встретить периодические или близкие к ним процессы, повторяющиеся через одинаковое время. Данные процессы относят к колебательным.

Таким образом, колебаниями является процесс, характеризуемый физической величиной, последовательно изменяющейся в ту или иную сторону относительно некоторого своего среднего значения. К примеру, на качелях, которые подвешены на веревках, человек отклоняется либо вперед и вверх, либо назад и вверх, относительно равновесного положения. В таком случае, качели являются колебательной системой.

Колебательный процесс в системе возникает при воздействии внутренних или внешних сил. Когда в системе наблюдаются колебания, являющиеся результатом внутреннего воздействия, их называют свободными. В том случае, когда колебания тела повторяются через определенное время, их относят к периодическим. Для возникновения свободных колебаний необходимы следующие условия:

положение устойчивого равновесия;

• избыточная механическая энергия тела для выхода системы из равновесного положения;
• действие возвращающей силы на тело, которая направлена к положению устойчивого равновесия;

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным. Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием. 

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника. 

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

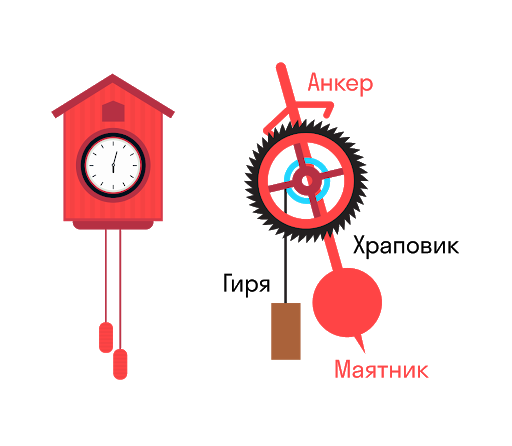
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Описание графика

Чтобы отобразить пружинные колебания, используется график, на котором показывается смещение тела со временем. На практике устанавливается к маятнику карандаш, а за ним бумажная лента. Последнее тело будет равномерно колебаться за счет перемещения. Можно провести опыт с помощью математического маятника.

В любом случае график ГК — синусоида либо косинусоида. По нему осуществляется определение характеристик вынужденного либо свободного колебания. В уравнении координата тела зависит от времени. На первом интервале косинус максимален, а синус равен нулю.

Если исследование начинать из положения полного равновесия, график повторяет синусоиду. При максимальном отклонении описывается косинус. Значение волны в разных точках определяется по формуле: w=π/2.

Скорость в крайних положениях равняется нулю. При прохождении равновесия она достигает максимума. Если проанализировать момент возникновения движения, уравнение зависимости, можно прийти к выводу, что скорость максимальна при тригонометрическом множителе -1 либо 1. Значение показателя вычисляется по формуле: Vmax=Aw.

Классификация системы

Свободные колебания выполняются под воздействием внутренних сил системы после её вывода из равновесия. Чтобы движения были гармоническими, нужно описать линейное уравнение. В системе нет диссипации энергии. При её ненулевом значении в системе после возбуждения приходит затухание.

Вынужденные движения совершаются под влиянием внешней силы, но с периодическим характером. Чтобы процесс был гармоническим, потребуется привести колебательную систему в линейную. При этом внешняя сила может меняться периодически как гармоническое колебание. В таком случае зависимость времени от силы будет носить синусоидальный характер.

Часто маленькие ГК вынужденного и свободного типа происходят в настоящих системах. Они могут принимать форму стандартных колебаний либо близким к ним движениям. В 1822 году Фурье открыл широкий класс функций периодического класса, который раскладывается на сумму тригонометрических составных компонентов. Таким способом формируется ряд Фурье.

Согласно такому утверждению, любое периодическое движение представлено в виде суммы ГК с соответствующими амплитудами, начальными фазами и частотами. К слагаемым этой суммы относится гармоническое колебание, характерна минимальная частота. Она называется основной. Само колебание считается первичной гармоникой либо главным тоном. Частоты других слагаемых, ГК, кратны основной частоте.

Такие колебания называются максимальными гармониками либо обертонами. Они могут быть первичными, вторичными. Приборы, функционирующие по такому принципу, обладают свойством линейности. Ученые установили связь воздействия и отклика, что называется устойчивой характеристикой системы. Подобная информация позволяет исследовать прохождение смещений, скачков, произвольных колебаний.

Практические учебники издаются по отдельным темам, разделам физики. Так как уравнение повторяет график синуса или косинуса, поэтому в практические занятия входят математические упражнения. Для некоторых координат характерны конкретные значения. Уравнение решается любым возможным математическим способом.

https://youtube.com/watch?v=7e6wA0mme6A

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​\( \nu \)​ < 16 Гц);
• звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
• ультразвук (\( \nu \) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Применение гармонических колебаний в жизни

Колебания часто встречаются в природе и технике. Как и вращение, колебательные процессы являются основой развития таких отраслей, как электротехника и радиотехника. Зачастую колебания носят негативный характер. К примеру, вибрируют крылья самолета, корпуса судов, здания и сооружения из-за резонанса с эксплуатируемым там оборудованием. Данное обстоятельство учитывают инженеры при реализации подобных проектов.

Колебания используют при создании музыкальных инструментов. Например, струны колеблются под руками музыканта, что вызывает колебания воздуха, и окружающие слышат звуки музыки.

Многие важные внутренние процессы в организме человека относят к колебательным. Например, человеческое сердце, находясь в состоянии покоя, совершает приблизительно одно колебательное движение в течение секунды. Повторяющиеся нервные импульсы провоцируют непрерывное сокращение и растягивание мышц. Люди слышат и говорят, благодаря колебаниям.

Свет также обладает колебательной природой. Кроме того, и атомы совершают колебательные движения. Гармоничные колебания тока активно применяются в производстве технических приборов.

В радиотехнике и электросвязи широко используют гармонические сигналы от долей Гц (инфранизкие частоты) до десятков и сотен ГГц (сверхвысокие частоты). Разнообразные звуки и изображения транспортируются на удаленные расстояния, благодаря электромагнитным волнам.

Колебания в природе

Различные колебания окружают нас повсюду. Большинство движений в природе, даже направленных, имеют, по крайней мере, небольшую колебательную составляющую.

Рис. 1. Колебания в природе.

Среди колебаний можно выделить периодические (волны, маятник), и непериодические (флаг на ветру). Главное их отличие в том, что каждое периодическое колебание очень похоже на предыдущие и последующие своими характеристиками. Изучение непериодических колебаний показывает, что любое из них может быть представлено бесконечной суммой периодических колебаний. Поэтому, описание любых колебательных процессов базируется на описании периодических колебаний.

Гармонические колебания и их закон

Изучение колебаний следует начать с построения их графика. По оси абсцисс будет отложено время $t$, а по оси ординат – отклонение $x$. Используется маятник с песком или красящим порошком, запускаются его колебания, а снизу протягивается лист, на котором остается след.

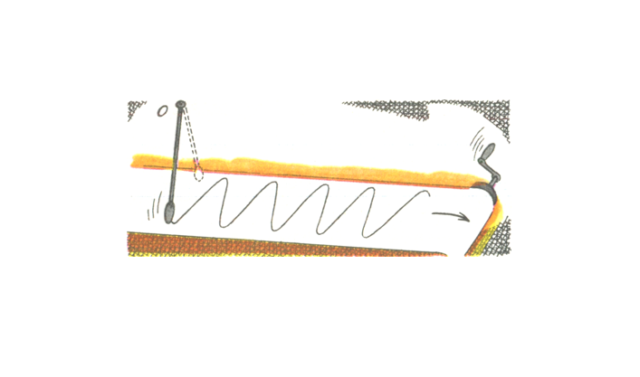Рис. 2. Запись колебаний маятника.

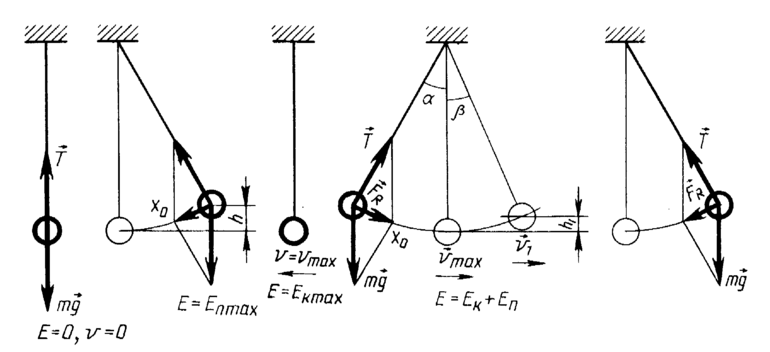
Кратко напомним, что причиной колебаний маятника является равнодействующая, которая в середине равна нулю, а в крайних положениях – максимальна и направлена против отклонения. Ускорение маятника изменяется точно также.

В теории высшей математики доказывается, что единственная функция, ускорение которой пропорционально отклонению, и направлено против отклонения – это синусоида $x=A sin(\omega t+\phi)$.

Колебания, подчиняющиеся закону синуса, называются гармоническими колебаниями. Параметр $A$ в приведенных формулах называется амплитудой, параметр $\omega$ – частотой (иногда круговой частотой) параметр $\phi$ – фазой (иногда – начальной фазой). Хорошими примерами гармонических колебаний могут являться также волны воды, движение груза на пружине, движение поршня в автомобильном двигателе.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

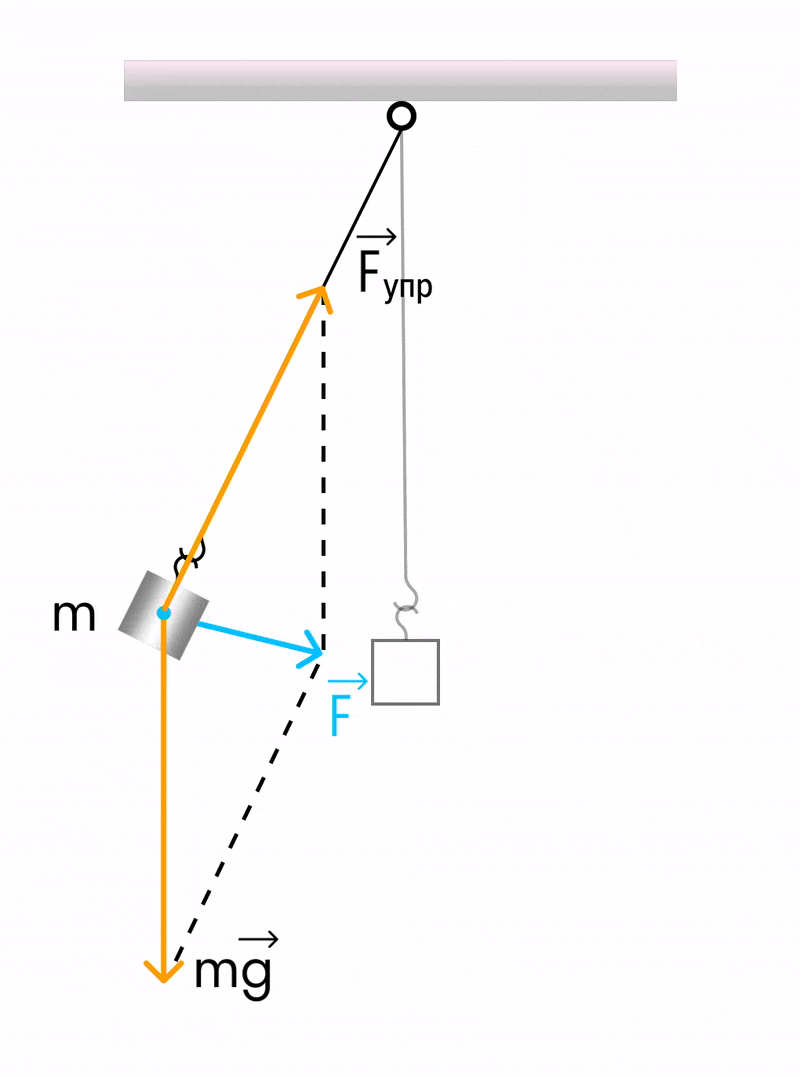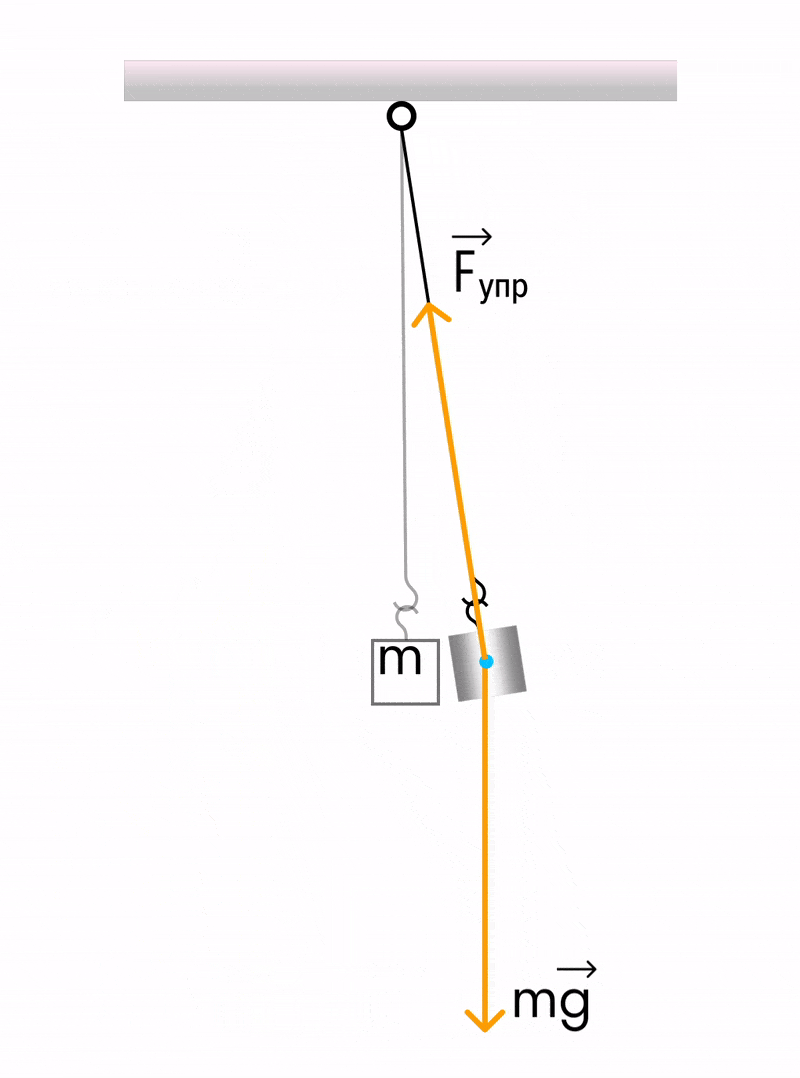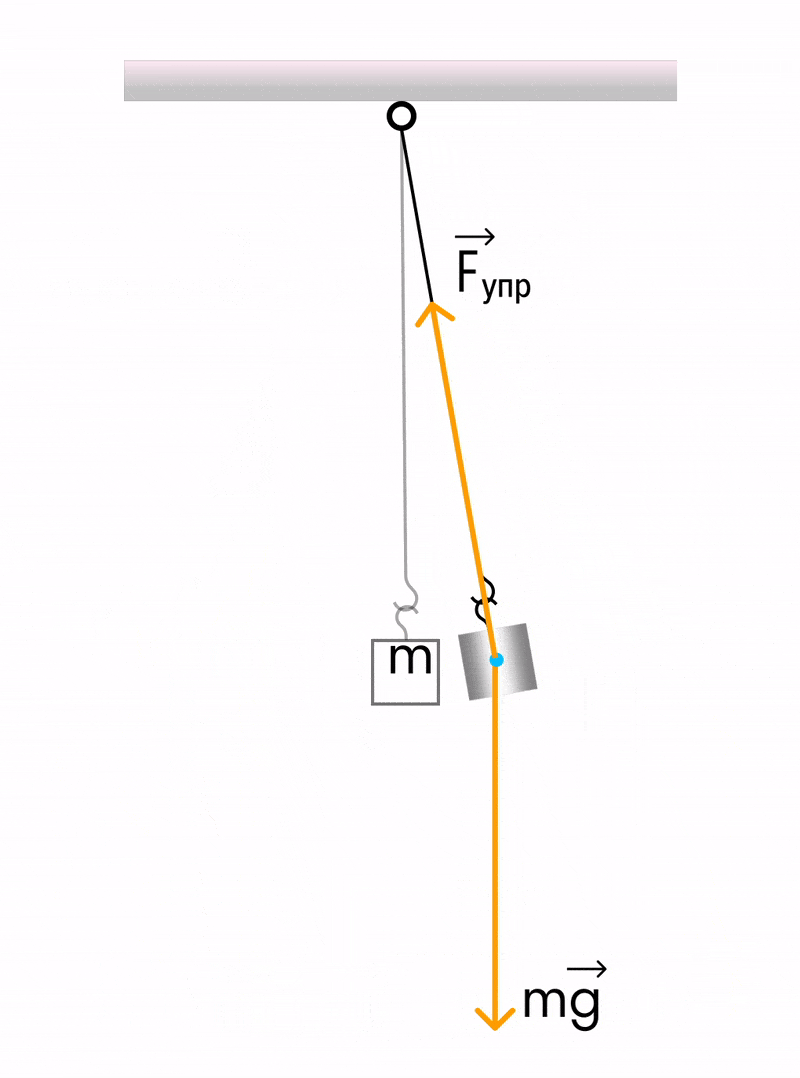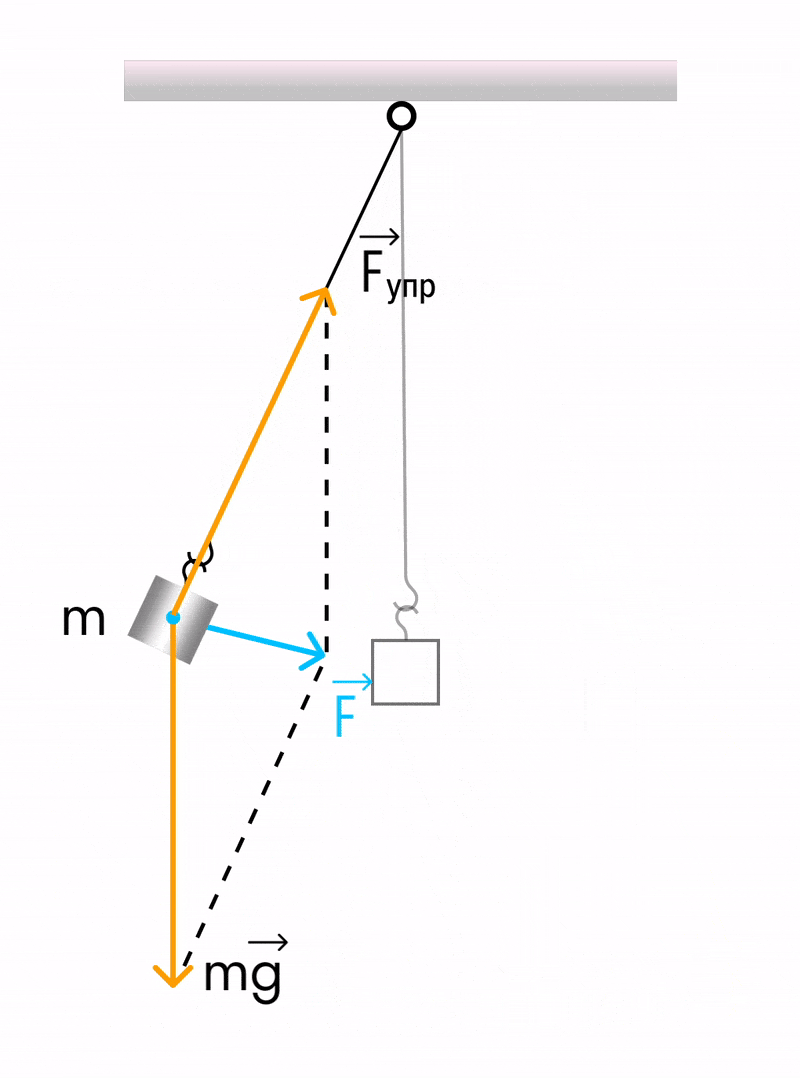
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника T — период l — длина нити g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 π = 3,14

Уравнение гармонических колебаний

В большом числе случаев на практике представляет интерес поведение системы, совершающей колебания не при всех возможных отклонениях, а только при очень небольших отклонениях.

В этом случае решение уравнения движения (1) существенно упрощается. Какой бы сложной не была функция силы, ее можно разложить в ряд Тейлора. При этом в реальных задачах физики отличным от нуля бывает $xF’(0)$, уравнение движения при очень небольших отклонениях от равновесия принимает вид:

$m\frac{d^2x}{dt^2}=xF’(0)=-kx (2),$

где введено обозначение: $F’(0)=-k>0$.

Уравнение вида (2) получается при исследовании многих явлений физики. В рассмотренном выше примере параметр $x$ — это расстояние от положения равновесия. Но $x$ можно понимать как заряд конденсатора, в колебательном контуре что-то иное.

Уравнение вида (2) называют уравнением гармонических колебаний, при этом систему, совершающую данные малые колебания, считают линейным (гармоническим) осциллятором.

Часто рассматриваемыми примерами гармонических осцилляторов в механике являются:

• тело на упругой пружине (пружинный маятник);
• тело на нерастяжимом и невесомом подвесе (нити) (математический маятник);
• физический маятник.

Уравнение гармонических колебаний обычно представляют в виде:

$\ddot {x}+\omega^2 x=0 (3),$

где $\omega^2=\frac{k}{m}>0$.

Гармонические колебания

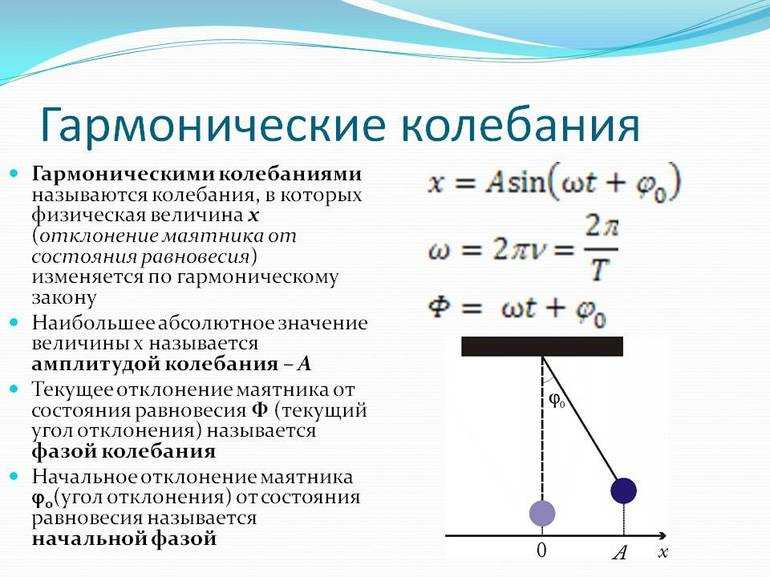
Гармонические колебания – простейшие периодические колебания, при которых координата тела меняется по закону синуса или косинуса:

где ​\( x \)​ – координата тела – смещение тела от положения равновесия в данный момент времени; ​\( A \)​ – амплитуда колебаний; ​\( \omega t+\varphi_0 \)​ – фаза колебаний; ​\( \omega \)​ – циклическая частота; ​\( \varphi_0 \)​ – начальная фаза.

Если в начальный момент времени тело проходит положение равновесия, то колебания являются синусоидальными.

Если в начальный момент времени смещение тела совпадает с максимальным отклонением от положения равновесия, то колебания являются косинусоидальными.

Скорость гармонических колебаний
Скорость гармонических колебаний есть первая производная координаты по времени:

где ​\( v \)​ – мгновенное значение скорости, т. е. скорость в данный момент времени.

Амплитуда скорости – максимальное значение скорости колебаний, это величина, стоящая перед знаком синуса или косинуса:

Ускорение гармонических колебаний
Ускорение гармонических колебаний есть первая производная скорости по времени:

где ​\( a \)​ – мгновенное значение ускорения, т. е. ускорение в данный момент времени.

Амплитуда ускорения – максимальное значение ускорения, это величина, стоящая перед знаком синуса или косинуса:

Если тело совершает гармонические колебания, то сила, действующая на тело, тоже изменяется по гармоническому закону:

где ​\( F \)​ – мгновенное значение силы, действующей на тело, т. е. сила в данный момент времени.

Амплитуда силы – максимальное значение силы, величина, стоящая перед знаком синуса или косинуса:

Тело, совершающее гармонические колебания, обладает кинетической или потенциальной энергией:

где ​\( W_k \)​ – мгновенное значение кинетической энергии, т. е. кинетическая энергия в данный момент времени.

Амплитуда кинетической энергии – максимальное значение кинетической энергии, величина, стоящая перед знаком синуса или косинуса:

При гармонических колебаниях каждую четверть периода происходит переход потенциальной энергии в кинетическую и обратно.
В положении равновесия:

• потенциальная энергия равна нулю;
• кинетическая энергия максимальна.

При максимальном отклонении от положения равновесия:

• кинетическая энергия равна нулю;
• потенциальная энергия максимальна.

Полная механическая энергия гармонических колебаний
При гармонических колебаниях полная механическая энергия равна сумме кинетической и потенциальной энергий в данный момент времени:

Важно!
Следует помнить, что период колебаний кинетической и потенциальной энергий в 2 раза меньше, чем период колебаний координаты, скорости, ускорения и силы. А частота колебаний кинетической и потенциальной энергий в 2 раза больше, чем частота колебаний координаты, скорости, ускорения и силы

Графики зависимости кинетической, потенциальной и полной энергий всегда лежат выше оси времени.

Если сила сопротивления отсутствует, то полная энергия сохраняется. График зависимости полной энергии от времени есть прямая, параллельная оси времени (в отсутствие сил трения).

Какое уравнение выражает смысл гармонического колебания

Согласно определению, гармонические колебания обладают кинематическими характеристиками, которые меняются по закону синуса или косинуса.

Визуализировать гармонические колебания можно, представив вращательное движение как колебательное движение вдоль двух осей, которые взаимно перпендикулярны. Предположим, что тело вращается по окружности с радиусом А. Начальное его положение совпадает с точкой С. В начале движения радиус-вектор, который описывает рассматриваемую точку, расположен под углом \(\varphi _{0}\) к оси ОХ.

По проекциям радиуса на оси можно рассчитать начальные координаты:

\(x_{0}=A\cos \varphi _{0}\)

\(y_{0}=A\sin \varphi _{0}\)

Можно предположить, что, спустя время t, тело, обладая угловой скоростью \omega, переместилось в точку D. В этом случае угол поворота радиус-вектора относительно начального положения равен \(\varphi.\) Текущие координаты тела будут равны:

\(x=A\cos (\varphi +\varphi _{0})\)

\(y=A\sin (\varphi +\varphi _{0})\)

Если речь идет о равномерном движении тела по окружности, то:

\(\varphi=\omega*t\)

Таким образом:

\(x=A\cos (\omega*t +\varphi _{0})\)

\(y=A\sin (\omega*t +\varphi _{0})\)

Записанные равенства представляют собой закон движения материальной точки, которая совершает гармонические колебания в контуре. Если \(\sin (90^{0}-\alpha )=\cos \alpha,\) то уравнение можно преобразовать следующим образом:

\(x=A\cos (\omega*t +\varphi _{0})=A\sin (\omega*t-90^{0} +\varphi _{0})=A\sin (\omega t+\varphi ^{,}_{0})\)

где \(\varphi ^{,}_{0} = \varphi _{0}-90^{0}\) является новым параметром, характеризующим некое другое начальное положение тела.

Исходя из представленных закономерностей, следует, что записанные уравнения являются в теории одинаковыми при разных начальных условиях. В качестве примера можно разобрать только первое уравнение. Каждый из введенных параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:

\(x=A\cos (\omega*t +\varphi _{0})\)

х — является текущей координатой тела;

А — это амплитуда колебаний (максимальное отклонение тела от положения равновесия);

\(\omega\) — определяет циклическую частоту колебания;

t — является временем движения;

\(\varphi _{0})\) — представляет собой начальную фазу колебания;

\((\omega*t +\varphi _{0}) \) — текущая фаза колебания (все, что стоит под тригонометрической функцией).

Обладая информацией об общем виде колебательного движения, можно определить зависимость скорости и ускорения от времени:

\(x=A\cos (\omega*t +\varphi _{0})\)

\(v_{x}=-A\omega \sin(\omega*t +\varphi _{0})\)

\(a_{x}=-A\omega^{2}\cos(\omega*t +\varphi _{0})\)

где \(v_{x}\) является скоростью тела, \(a_{x}\) – это его ускорение.

Таким образом:

\(a_{x}=-\omega^{2}x\)

Данное уравнение является основным уравнением гармонических колебаний, которое часто встречается при решении задач.

Гармонические колебания пружинного маятника

В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения

С этой целью важно знать, от чего зависят частота и период колебаний

Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:

Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.

Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.

С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).

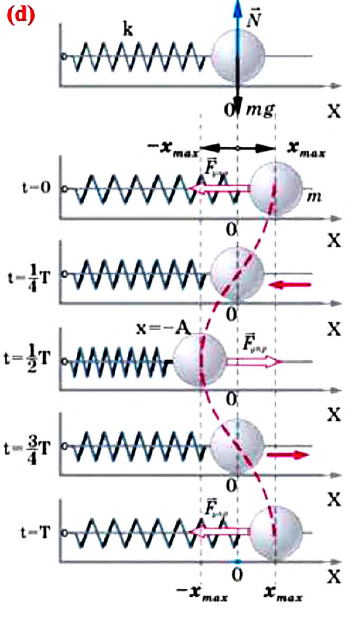
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:

или

Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.

Где  — масса шарика, закрепленного на пружине, — проекция ускорения шарика вдоль оси  — жесткость пружины, -удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение — постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения — известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение соответствует квадрату циклической частоты

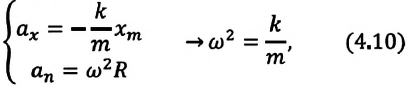
или

Таким образом, уравнение движения пружинного маятника можно записать и так:

Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:

Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.

Здесь фаза колебания, — начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах: Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы В этом случае формулу гармонических колебаний пружинного маятника можно записать так:

или

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника: 

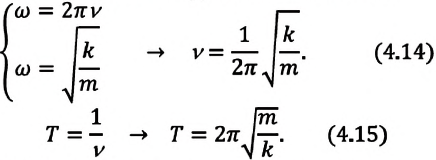
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.

1.3. Свободные гармонические колебания в LC-контуре

1. Электромагнитный контур состоит из плоского конденсатора емкостью С и катушки индуктивности (соленоида) с индуктивностью L. Такой контур называется идеальным контуром с распределенными параметрами. Конденсатор зарядили, на одной пластине заряд +q, на другой (–q). Рассмотрим процессы в LC – контуре за время T, называемое периодом колебаний.

Момент времени t = 0. Конденсатор заряжен, ключ «К» разомкнут, ток в контуре не идет: I = 0, ,

Ключ замкнут, по цепи идет ток разрядки до тех пор, пока не выровняются потенциалы обкладок конденсатора. При

Когда конденсатор разрядится, ток разрядки прекратится. Магнитное поле в катушке индуктивности, не поддерживаемое током, начнет уменьшаться. Уменьшение магнитного поля вызовет уменьшение магнитного потока сквозь площадь катушки, возникнет ЭДС индукции. По цепи контура пойдет индукционный ток того же направления, что и ток разрядки (правило Ленца). Это приведет к перезарядке конденсатора. При

Направление тока разрядки в контуре изменится. Ток разрядки будет идти по цепи до выравнивания потенциалов на обкладках конденсатора.

При

При t = T система вернется в исходное положение.

В рассмотренном LC – контуре происходит превращение энергии из одного вида в другой и обратно, полная энергия контура — величина постоянная _.

Периодические изменения вектора напряженности Е электрического поля и вектора магнитной индукции В магнитного поля в закрытом колебательном LC – контуре называется электромагнитными колебаниями.

2. Используем 2-й закон Кирхгофа для получения дифференциального уравнения электромагнитных колебаний.

Для любого замкнутого контура алгебраическая сумма падений напряжений на всех его участках равна алгебраической сумме ЭДС, действующих в этом контуре (2-ой закон Кирхгофа).

Падение напряжения на обкладках конденсатора в LC – контуре равно

где q – величина заряда на обкладках, С – емкость конденсатора. ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, определяется формулой: (закон Фарадея для самоиндукции).

Второй закон Кирхгофа для LC – контура имеет вид:

или .

По определению сила тока равна первой производной по времени от заряда , тогда .

Преобразуем уравнение 2-ого закона Кирхгофа, получим

Обозначим , получим окончательно уравнение вида:

Это линейное дифференциальное уравнение второго порядка, решениями которого являются уравнения:

или .

И дифференциальное уравнение для электромагнитных колебаний, и его решения подобны тем, которые получены для механической системы (пружинного маятника).

Величины, входящие в уравнения электромагнитных колебаний, имеют следующий смысл:

q – амплитуда заряда – максимальный заряд конденсатора;

q – величина заряда на обкладках конденсатора в момент времени t;

– фаза колебаний – величина, определяющая заряд конденсатора в любой момент времени t;

α – начальная фаза определяет заряд конденсатора в начальный момент времени (t = 0).

Циклической частотой периодических колебаний в LC – контуре является величина .

Период колебаний равен (формула Томсона).

Определим зависимость силы тока, ЭДС и энергии колебаний от времени в LC – контуре. Уравнение изменения заряда на обкладках конденсатора возьмем в виде:

Сила тока в контуре определяется соотношением:

.

Величину называют амплитудой силы тока.

Уравнение для ЭДС имеет вид:

.

Величина – амплитуда ЭДС.

Электрическая и магнитная энергия изменяется согласно уравнениям:

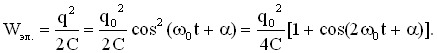
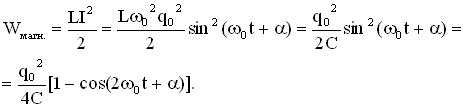
Полная энергия колебаний в LC — контуре не зависит от времени (закон сохранения энергии).

Графики зависимостей от времени t физических величин, характеризующих электромагнитных колебаний в LC – контуре, аналогичны графикам для механических колебаний (см. Рисунок 1.2).

Если заряд на обкладках изменяется по закону , т.е. начальная фаза α = 0, то его график такой же как график смещения.

Напряжение между обкладками конденсатора изменяется по тому же закону, что и заряд конденсатора, только амплитуда напряжения будет другой .

Изменение силы тока аналогично изменению скорости тела при механических незатухающих колебаниях. W_эл. изменяется как W_пот., а W_магн. — как W_кин..

Применение маятников

Для вычисления энергии гармонических колебаний используются на практике разные приборы, включая осциллятор. Он представлен в виде математического маятника со специальной механической системой. Последние элементы находятся в невесомости, в однородном поле сил тяготения. Период незначительных вертикальных колебаний не зависит от амплитуды. Параметр вычисляется по следующей формуле: T=2π √l/g.

Если для опыта используется физический маятник, твердое тело смещается в поле конкретных сил относительно материальной точки, которая не является центром масс тела. Когда учитывается неподвижная ось, колебания перпендикулярны направлению действия сил и не проходят через центр масс тела. В некоторых точках значение равняется нулю либо достигают максимума.

Чтобы найти значение стоячей волны, потребуется рассмотреть колебания в системе с амплитудой узловой. Подобное явление наблюдается в результате отражения волны от преграды. Для расчёта учитывается количество фаз, частота, коэффициент затухания волны в точке отражения. Подобные колебания создают струны, воздух в трубе.

Процесс считается последовательным. При этом у него установлена тесная связь с вектором напряжения, магнитным полем. Одновременно изменяется магнитное поле, провоцирующее колебания в электрическом поле. Чтобы теоретически описать природные явления, используется монохроматическая волна.

Отличие этой модели заключается в том, что в спектр входит только одна составляющая по частоте волна:

• строго гармоническая;
• имеет постоянную частоту;
• имеет начальную фазу;
• имеет амплитуду.