2.2. RLC-контур. Свободные колебания window.top.document.title = «2.2. RLC-контур. Свободные колебания»;
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис. 2.2.1).
| Рисунок 2.2.1.Последовательный RLC-контур |
Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
qqtRLC
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда
Здесь принято обозначение: Уравнение (*) описывает свободные колебания в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных колебаний груза на пружине в отсутствие сил трения (ч. I, § 2.2). Рис. 2.2.2 иллюстрирует аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.
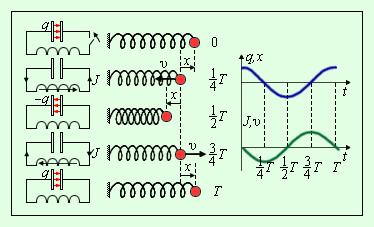 |
| Рисунок 2.2.2.Аналогия процессов свободных электрических и механических колебаний |
Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице 1.
|
||||||||||||||||||||||||||||||||||
| Таблица 1 |
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний
Амплитуда q и начальная фаза φ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение 2, q = C, φ = 0.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рис. 2.2.3).
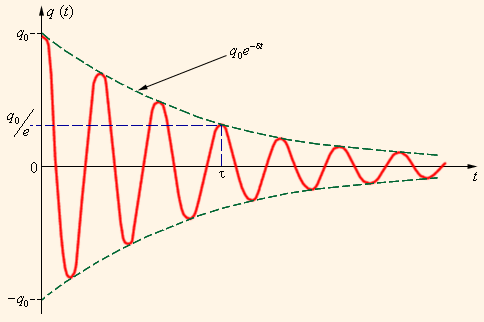 |
| Рисунок 2.2.3.Затухающие колебания в контуре |
Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: Fтр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид
Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция
exp (–δt)Re ≈ 2,7 разавременем затухания
NQ
Для RLC-контура добротность Q выражается формулой
Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.
Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.
 |
|
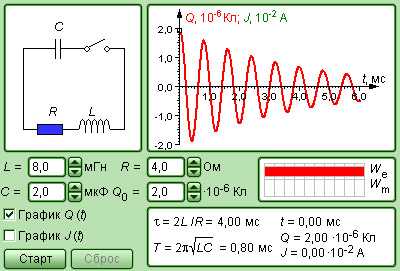
Модель. Свободные колебания в RLC-контуре |
Глоссарий по физике
А
Б
В
Г
Д
Е
Ж
З
И
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
Добротность колебательной системы
|
Добротность колебательной системы
—
безразмерный коэффициент, величина которого характеризует
резонансные свойства линейной колебательной системы, отношение запасённой в
системе энергии W к мощности потерь Р за период
колебаний, т. е. Q =
2πωW/P. Теоретически определяется путём условного
разграничения диссипативных и реактивных элементов. Практически часто
измеряется как отношению резонансной частоты ω к ширине
резонансной кривой
Δω на уровне убывания амплитуды в ~2 раза: Q = ω/Δω,
что характерно для Гауссова распределения спектра частот уединенного
резонатора.
В случае электрических контуров запасённую энергию считают сосредоточенной
в чисто реактивных элементах
индуктивности L и ёмкости С, а потери связывают с протеканием
тока по чисто диссипативному элементу — сопротивлению R. Тогда
Соответственно для механической колебательной системы с массой m,
упругостью k и коэфициентом
трения b
В колебательных системах с большой добротностью частота и коэффициент
затухания a слабозатухающих колебаний вида
e-atsinωt связаны с добротностью отношением:
Q = ω/2a = π/d [циклов/долю] >> 1,
Рабочая добротность
—
это величина Qi, с которой связан отвод энергии
в полезную нагрузку.
В случае многомодовых систем
с дискретным (точнее, квазидискретным) спектром собственных частот каждая из
мод обладает своей добротностью; в пределе, когда спектр сливается в сплошной,
понятие добротности утрачивает смысл.
Литература по добротности колебательных систем
- Cтрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964;
- Горелик Г. С., Колебания и волны, 2 изд., М., 1959;
А. Миллер
к библиотеке
к оглавлению
FAQ по эфирной физике
ТОЭЭ
ТЭЦ
ТПОИ
ТИ
Знаете ли Вы, что в 1974 — 1980 годах профессор Стефан Маринов из г. Грац, Австрия, проделал серию экспериментов, в которых показал, что Земля движется по отношению к некоторой космической системе отсчета со скоростью 360±30 км/с, которая явно имеет какой-то абсолютный статус. Естественно, ему не давали нигде выступать и он вынужден был начать выпуск своего научного журнала «Deutsche Physik», где объяснял открытое им явление. Подробнее читайте в FAQ по эфирной физике.
НОВОСТИ ФОРУМАРыцари теории эфира |
10.11.2021 — 12:37: ПЕРСОНАЛИИ — Personalias -> — Карим_Хайдаров.10.11.2021 — 12:36: СОВЕСТЬ — Conscience -> — Карим_Хайдаров.10.11.2021 — 12:36: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 12:35: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОЙНА, ПОЛИТИКА И НАУКА — War, Politics and Science -> — Карим_Хайдаров.10.11.2021 — 12:34: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:18: НОВЫЕ ТЕХНОЛОГИИ — New Technologies -> — Карим_Хайдаров.10.11.2021 — 09:18: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:16: ЭКОЛОГИЯ — Ecology -> — Карим_Хайдаров.10.11.2021 — 09:15: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров.10.11.2021 — 09:13: ВОСПИТАНИЕ, ПРОСВЕЩЕНИЕ, ОБРАЗОВАНИЕ — Upbringing, Inlightening, Education -> — Карим_Хайдаров. |
От чего зависит добротность динамика?
Выше уже обсудили все моменты, которые могут ответить на этот вопрос. Остаётся только повторить, но попробуем коротко и по иному.
Добротность динамика зависит от некоторых следующих факторов:
- Мощный мотор. Низкая добротность будет у динамика, у которого имеется мощная катушка.
- Жесткость подвеса. Высокая добротность у динамика, имеющего большую жесткость. У него остаётся больше энергии в подвесах и центровочных шайбах.
- Масса подвижной системы. С массивным подвесом (утяжеленном диффузором и дополнительными центровочными шайбами) “мотору” тяжелее работать, а потери на “трение” возрастают – добротность будет расти, а резонанс падать (резонансная частота будет ниже).
- Провода. При большом сопротивлении проводов – увеличивается добротность. К примеру, добротность динамика будет больше в два раза, если к динамику, с сопротивлением катушки 4 Ома, подключать провода с сопротивлением 4 Ома.
- Оформление корпуса. В “закрытом ящике” воздух “заперт” и он создаёт дополнительное сопротивление диффузору. Жесткость подвеса больше, а соответственно, растёт и добротность. В акустике с фазоинвертором практически так же. Но тут уже будет две добротности – одна от динамика, вторая от самого корпуса.
В любом случае, будет лучше, если брать динамик с добротностью на любых резонансах от 0,3 до 0,7. И это не зависит от самого оформления корпуса акустики – с фазоинвертором это будет колонка или “закрытый ящик”.
Что такое – добротность динамика?
Пожалуй, сначала вопрос. А для чего вам вообще нужно знать этот параметр? Что он вам даст? Ведь этот параметр не скажет о том, на сколько хорошо или плохо сделан ваш динамик? На сколько хорошо он будет играть? Но когда возникает вопрос о доработке акустики, параметры добротности динамиков могут многое рассказать о технических возможностях будущей системы.
Но для полной картины возможностей динамика нужно будет собрать кучу параметров. В кругах “продвинутых” меломанов эти параметры называют – “параметры Тиля-Смолла”.
Измерением этих параметров точно не будем заниматься, по крайней мере – не в этот раз. Но о таком параметре как – добротность, поговорим немного. Без научных выкладок и “глубокой физики”. Порассуждаем по простому, что бы стало немного понятнее – какая добротность динамика лучше и почему?
Если проще, то речь идет про затухающие колебания. Так как разговор идет относительно динамика, то как он (динамик) ведет себя после подачи на него сигнала, как быстро затухают колебания диффузора при прекращении подачи сигнала на динамик.
Что такое – “запасы энергии в системе”?
Как найти резонанс параллельного колебательного контура на практике
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:
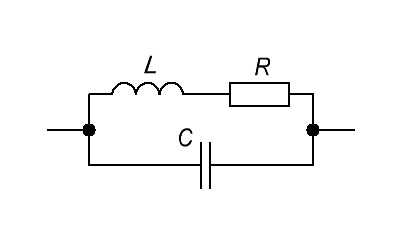
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:
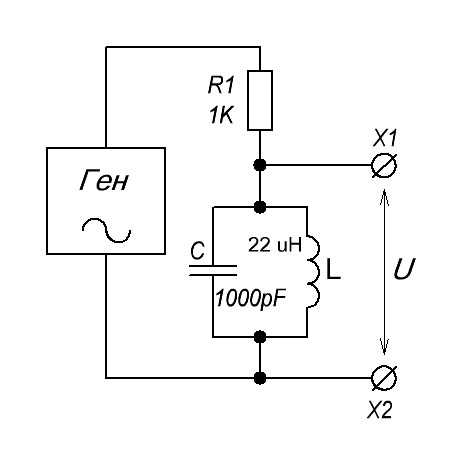

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.
Упрощенная схема будет выглядеть вот так:
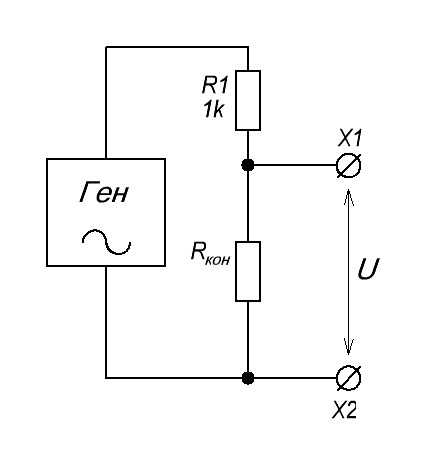
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
200 Герц.
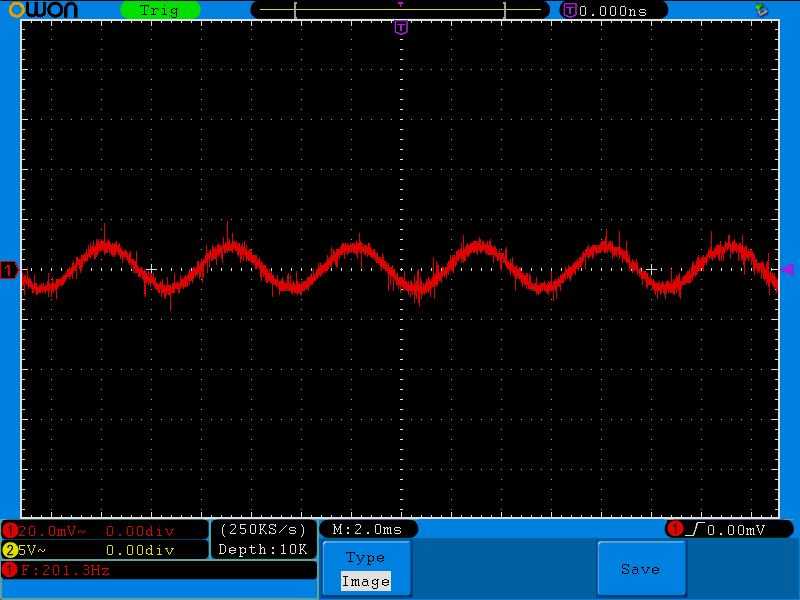
Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца
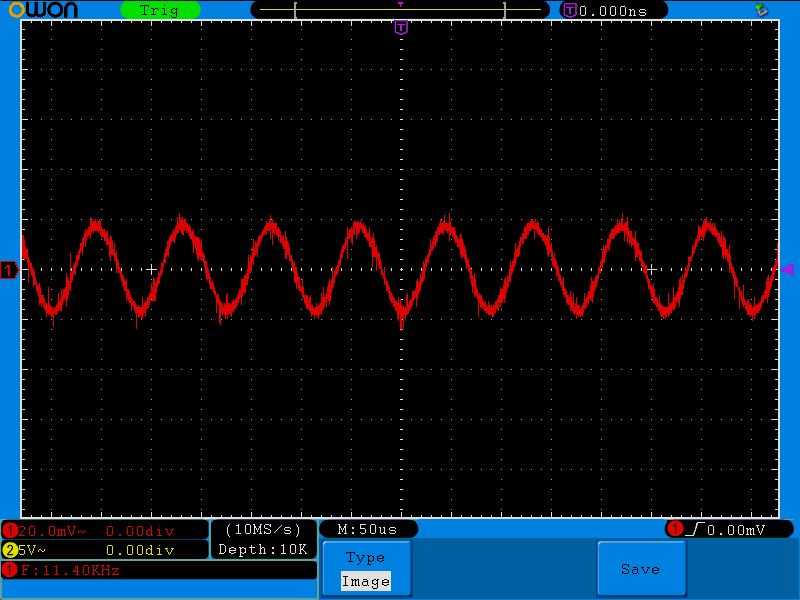
Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц
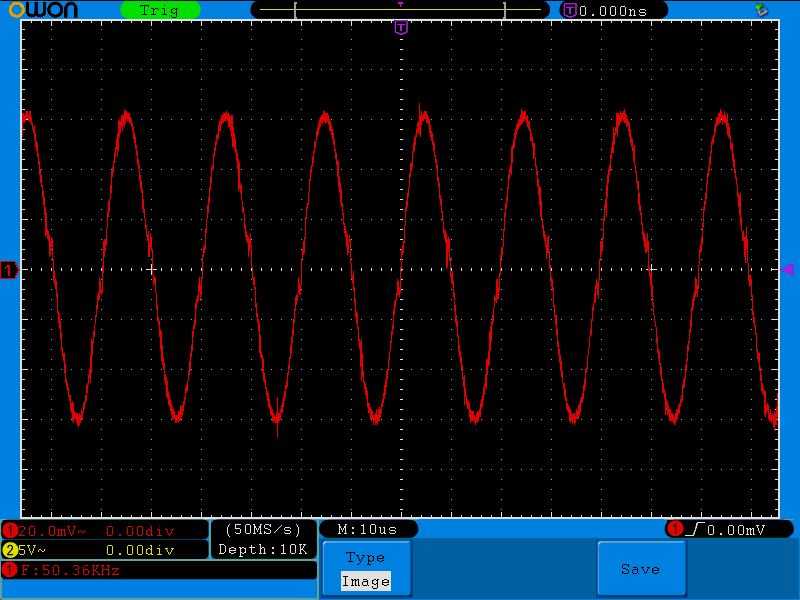
Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
723 Килогерца
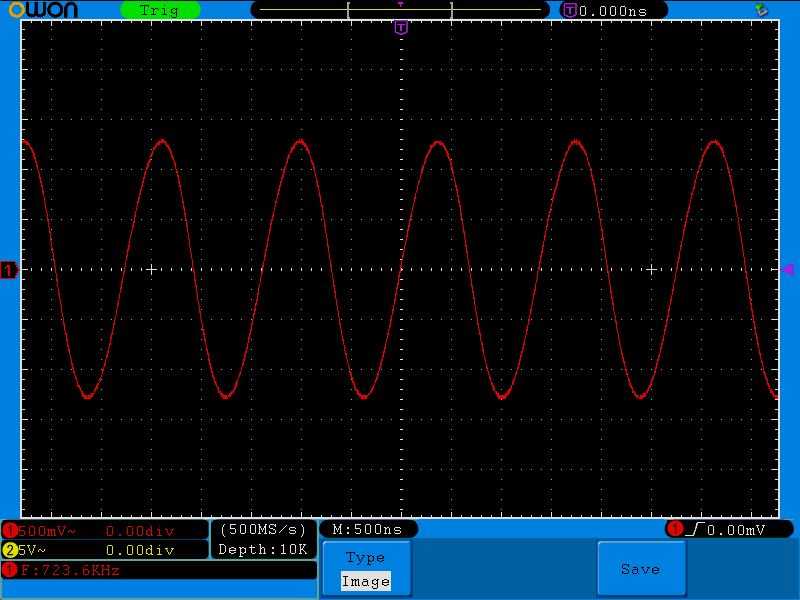
Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик
Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
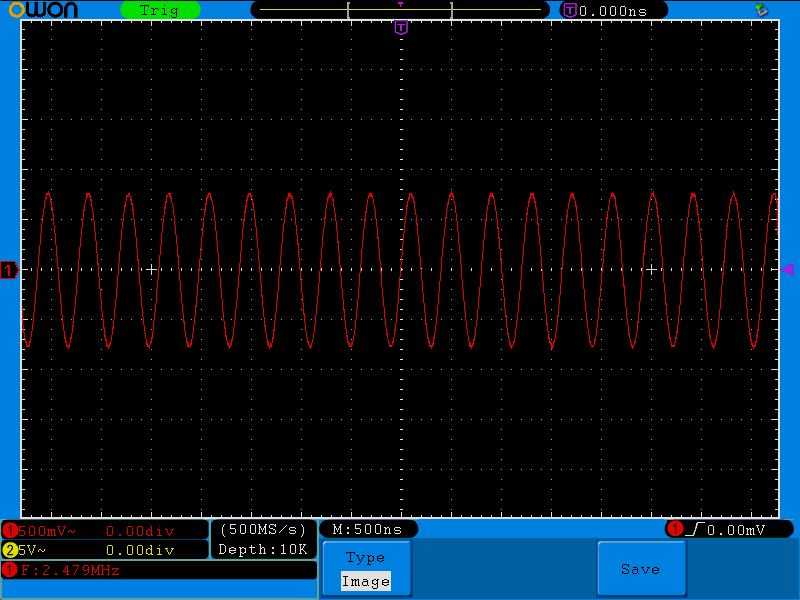
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре
Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам
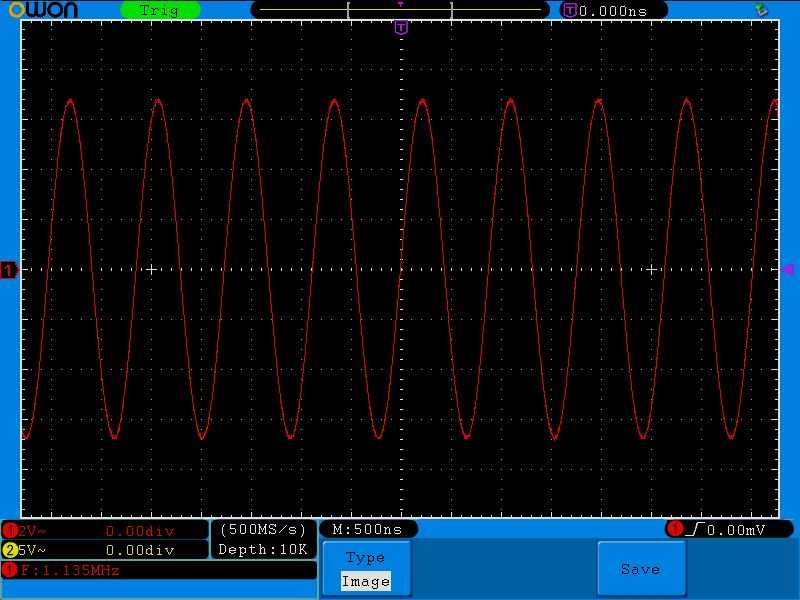
Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:
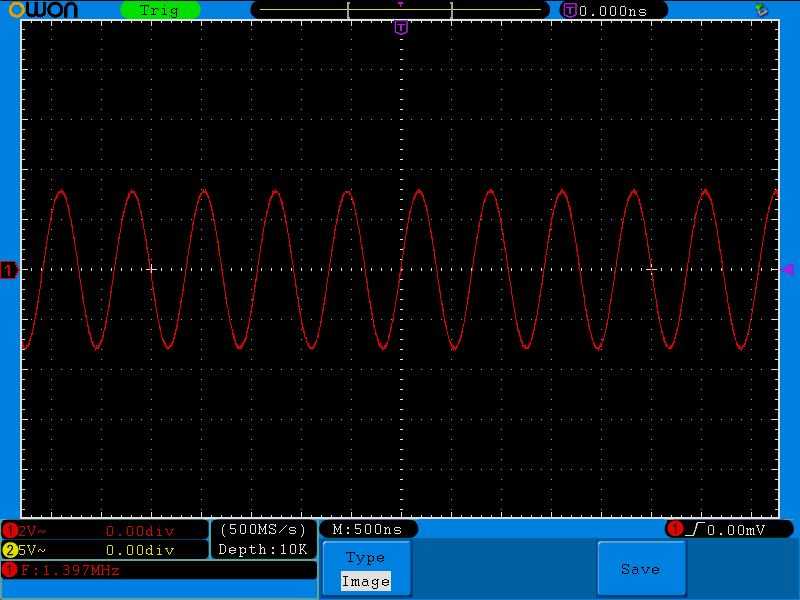
Снова добавляем частоту и видим, что напряжение стало еще меньше:
Высокая и низкая добротность динамика.
Динамик имеет высокую добротность, если колебания диффузора продолжаются на резонансной частоте даже тогда, когда на динамик уже не подается сигнал, а потери, при этом, очень маленькие. Про резонансные частоты поговорим в другой раз.
А вот если колебания динамика затухают практически сразу, после пропадания сигнала на него, и много сил динамик тратит на разного рода потери, то говорят, что такой динамик имеет низкую добротность.
Что бы не слышать в своих колонках “эффект переотраженки”, звуков типа “гула” или “бубнения”, не слушать “доигрывание” каких либо звуков, при доработке акустики или изготовлении её самостоятельно, нужно подбирать динамики с низкой добротностью.
Сказать иначе можно так – после пропадания сигнала от усилителя, динамик должен сразу возвращаться на своё место, которое он обычно занимает, когда на него не подаётся ни какой сигнал. Это будет идеальным вариантом, идеальным динамиком. Таким образом мы будем получать от динамика именно тот звук, который хотим услышать.
Принцип работы параллельного колебательного контура
Давайте подцепим к генератору частоты реальный параллельный колебательный контур
Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье .
Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.
Реактивное сопротивление катушки выражается по формуле
а конденсатора по формуле
Более подробно про это можно прочитать в этой статье.
Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.
Электрическая добротность динамика.
Интересный момент, когда динамик пытается вернуть диффузор в своё первоначальное состояние, после снятия электрического сигнала, катушка динамика вырабатывает ЭДС, двигаясь в магнитном поле. Динамики, в свою очередь, непосредственно подключены к усилителю, аудиопроводом.
Усилитель имеет практически нулевое сопротивление. И когда сигнал от усилителя пропадает, а динамик «на ходу», то он (динамик) работает как генератор. Причем, работает как генератор, с максимальной нагрузкой (выходы катушки практически закорочены сопротивлением усилителя). Эта нагрузка создает достаточно мощную тормозящую силу, вынуждающую катушку и диффузор быстро останавливаться.
Среднее значение электрической добротности (Qes), для низкочастотного динамика – от 0,2 до 0,9, но чаще – близкий к единице. И если сравнивать параметры электрической добротности со значениями механической добротности, то получается вывод – гашение колебаний (потеря энергии) происходит, в основном, из-за электрической составляющей.
Резонанс напряжений
Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

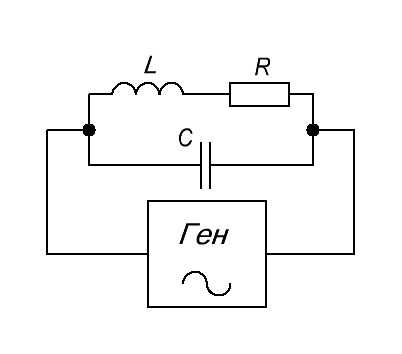
Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.
Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!
Ну что же, приступим ;-). Давайте сначала посчитаем резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.
Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:
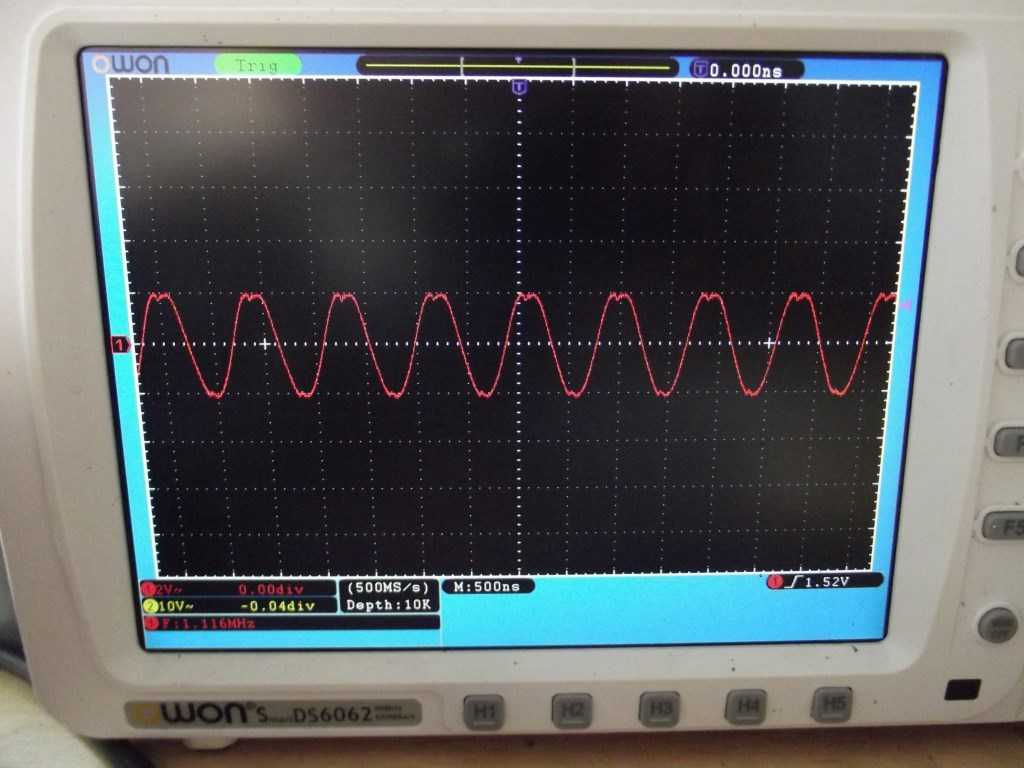
Размах амплитуды 4 Вольта
Хотя на генераторе частоты размах более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол ![]()
Вот этот сигнал мы подаем на наш последовательный колебательный контур:
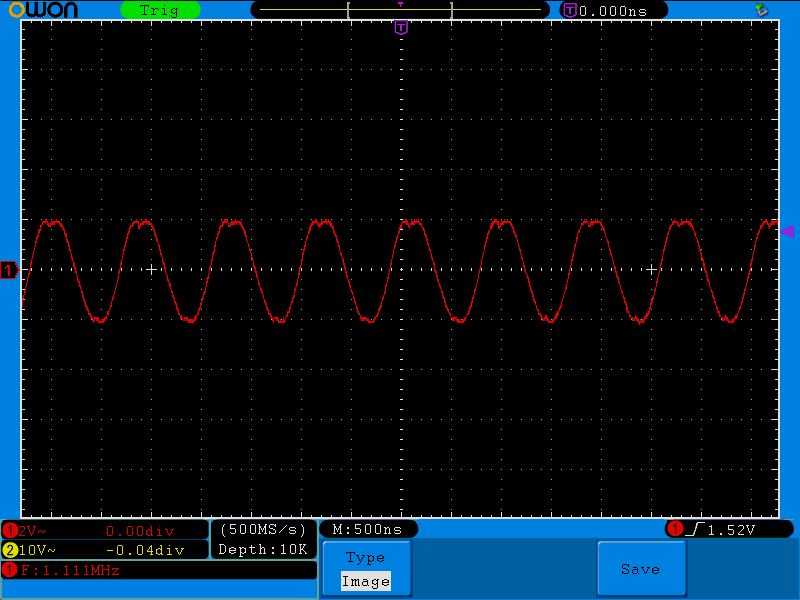
Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.
Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:
Смотрим напряжение на конденсаторе:
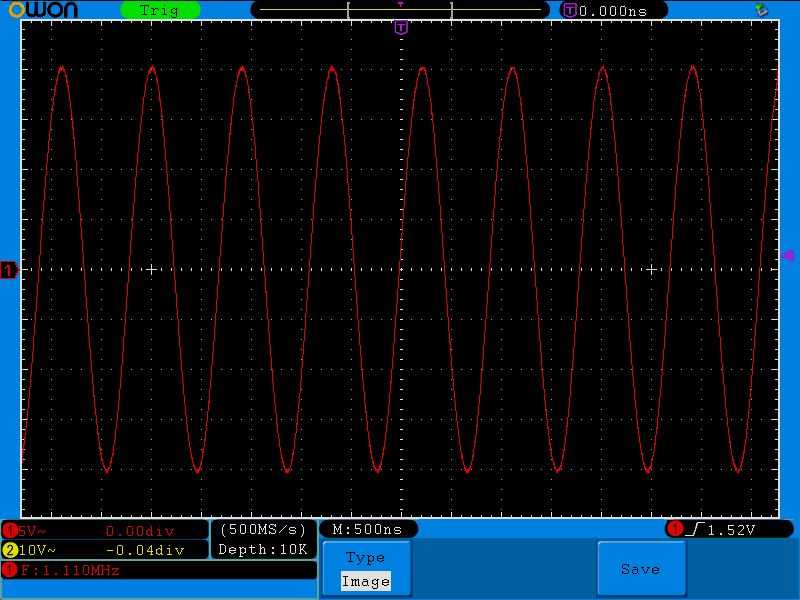
Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:
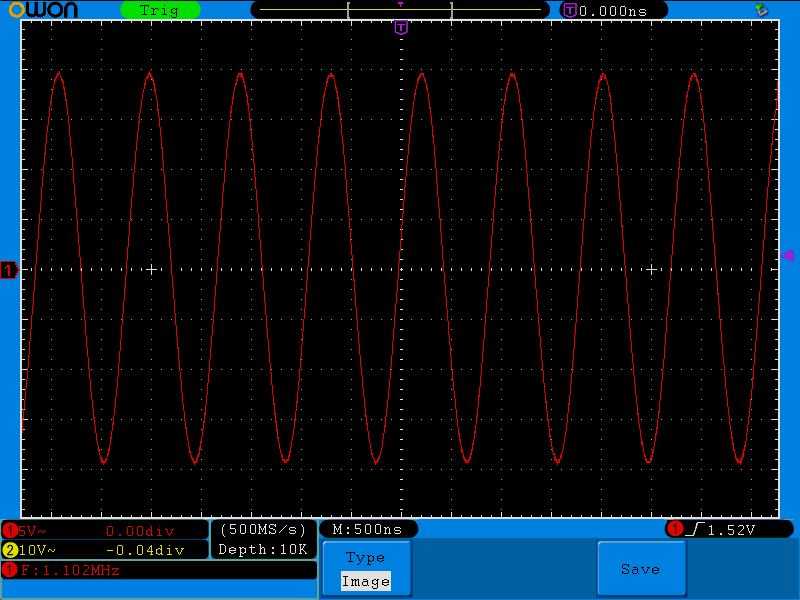
Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!
Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14, и цепляю поочередно к ним лампочку:


Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!
Объяснение резонанса напряжения
При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.
При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение UL = IXL , а на конденсаторе UC = IXC . А так как при резонансе у нас XL = XC , то получаем что UL = UC , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.






























