Замкнутый теодолитный ход: обработка и методика рассчета координат

Обработка результатов измерений

Мало знать точки, может произойти невязка. Для качественного выполнения полевой работы необходимо знать углы, с помощью которых строится то или иное пространство.

Для начала составляют проект, от которого будут отталкиваться на местности, часто это делается онлайн. Вычисление координат геодезических обоснований – важный шаг в работе.

Чтобы качественно обработать полученные результаты измерений, необходимо:

1. Составить таблицу с полученными углами.

2. Выписать точки начала и конца.

3. С помощью различных формул вычисляется сумма углов, а также длина. Расчет оформляется на отдельном полотне.

4. Далее необходимо вычислить теоретическую сумму для того, чтобы составить верное построение. Для каждого построения свои формулы.

Определение дирекционных углов

При известном значении дирекционного угла (\(\alpha \)) одной стороны и горизонтального (\(\beta \)) можно определить значение следующей стороны:

\(\alpha _{n+1}=\alpha _{n}+\eta \)

\(\eta =180^{\circ}-\beta _{пр}\)

\(\beta _{пр}\)– значение правого по ходу угла, из чего следует:

\(\alpha _{n+1}=\alpha _{n}+180^{\circ}-\beta _{пр}\)

Для левого (\(\beta _{лев}\)) эти знаки будут противоположными:

\(\alpha _{n+1}=\alpha _{n}-180^{\circ}+\beta _{лев}\)

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

Поскольку значение дирекционного угла не может быть больше, чем \(360^{\circ}\), то из него, соответственно, отнимают \(360^{\circ}\). В случае с отрицательным углом, необходимо к предыдущему \(\alpha \) добавить \(180^{\circ}\) и отнять значение \(\beta _{испр}\).

Приращения координат

Для приращений координат в замкнутом ходе применяют формулы, использующиеся при решении прямой геодезической задачи. Ее суть состоит в том, что по известным значениям координат исходного пункта, дирекционного угла и горизонтального приложения можно определить координаты следующего. Исходя из этого, формула приращения значений будет иметь следующий вид:

\(\Delta X = d\cdot cos \alpha \)

\(\Delta Y = d\cdot sin \alpha \)

d-горизонтальное проложение;
α-горизонтальный угол.

Для полигона, который имеет вид замкнутой геометрической фигуры, теоретическая сумма приращений будет равняться нулю для обеих координатных осей:

\(\sum \Delta X_{теор}= 0\)

\(\sum \Delta Y_{теор}= 0\)

Примеры

Решение прямой геодезической задачи

Для решения прямой геодезической задачи, неоходимо создать объект класса .

var directEllipsoid = new DirectProblemService(new Ellipsoid());
var directSpheroid = new DirectProblemService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для решения прямой задачи вызвать метод , в который передать в качестве параметров, начальную точку, азимут = направление и расстояние:

var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N);
var azimuth = 21;
var distance = 2000;
var directAnswer = directEllipsoid.DirectProblem(point1, azimuth, distance);

Ответ содержит вторую точку ортодромии и обратный азимут .

Решение обратной геодезической задачи

Для решения обратной геодезической задачи, неоходимо создать объект класса .

var inverseEllipsoid = new InverseProblemService(new Ellipsoid());
var inverseSpheroid = new InverseProblemService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для решения обратной задачи вызвать метод , в который передать в качестве параметров, две точки:

var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N);
var point2 = new Point(59, 36, 30, CardinalLongitude.W, 13, 5, 46, CardinalLatitude.N);
var inverseAnswer = inverseEllipsoid.OrthodromicDistance(point1, point2);

Ответ содержит прямой и обратный азимуты , , а также расстояние между точками .

Вычисление точки пересечения ортодромий

Для вычисления точки пересечения ортодромий, неоходимо создать объект класса .

var intersectEllipsoid = new IntersectService(new Ellipsoid());
var intersectSpheroid = new IntersectService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для рассчёта вызвать метод , в который передать в качестве параметров, по две точки для каждой из двух ортодромий:

var point1 = new Point(22, 36, 30, CardinalLongitude.E, 13, 5, 46, CardinalLatitude.N);
var point2 = new Point(27, 25, 53, CardinalLongitude.E, 15, 7, 38, CardinalLatitude.N);
var point3 = new Point(20, 36, 30, CardinalLongitude.E, 17, 5, 46, CardinalLatitude.N);
var point4 = new Point(26, 25, 53, CardinalLongitude.E, 13, 7, 38, CardinalLatitude.N);
var intersectCoord = intersectEllipsoid.IntersectOrthodromic(point1, point2, point3, point4);

Ответом будет точка — объект класса , в котором определены долгота и широта, в десятичных градуса (,) или в радианах (,).

Вычисление широты по долготе или долготы по широте

Для рассчётов, неоходимо создать объект класса .

var intermediateEllipsoid = new IntermediatePointService(new Ellipsoid());
var ntermediateSpheroid = new IntermediatePointService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для вычисления широты вызвать метод , в который передать значение долготы, для которого мы вычисляем широту, и две координаты характеризующие ортодромию.

var coord1 = new Point(10, 10);
var coord2 = new Point(30, 50);
var lat = intermediateEllipsoid.GetLatitude(20, coord1, coord2);

Для вычисления долготы вызвать метод , в который передать значение широты, для которого мы вычисляем долготу, и две координаты характеризующие ортодромию.

var coord1 = new Point(10, 10);
var coord2 = new Point(30, 50);
var lat = intermediateEllipsoid.GetLongitude(20, coord1, coord2);

В обоих случая ответом будет значение типа .

В каких случаях прокладывают

Начальная и конечная точка разомкнутого хода должна быть закреплена к пункту Государственной геодезической сети (ГГС) с уже определенными координатами и углами.

Если привязка к опорной точке осуществляется только для одной стороны, такой ход называют висячим. Также достаточно часто разомкнутый ход строят внутри крупных полигонов или сетей сгущения. Это необходимо для того, чтобы в дальнейшем провести подробную съемку ситуации. В таком случае его называют диагональным.

Построение разомкнутого теодолитного хода обусловливается особенностью объекта съемки, который может представлять собой:

– автомобильные и железные дороги;

– трубопроводы;

– реки;

– линии электропередач и связи.

– другие сооружения линейного типа.

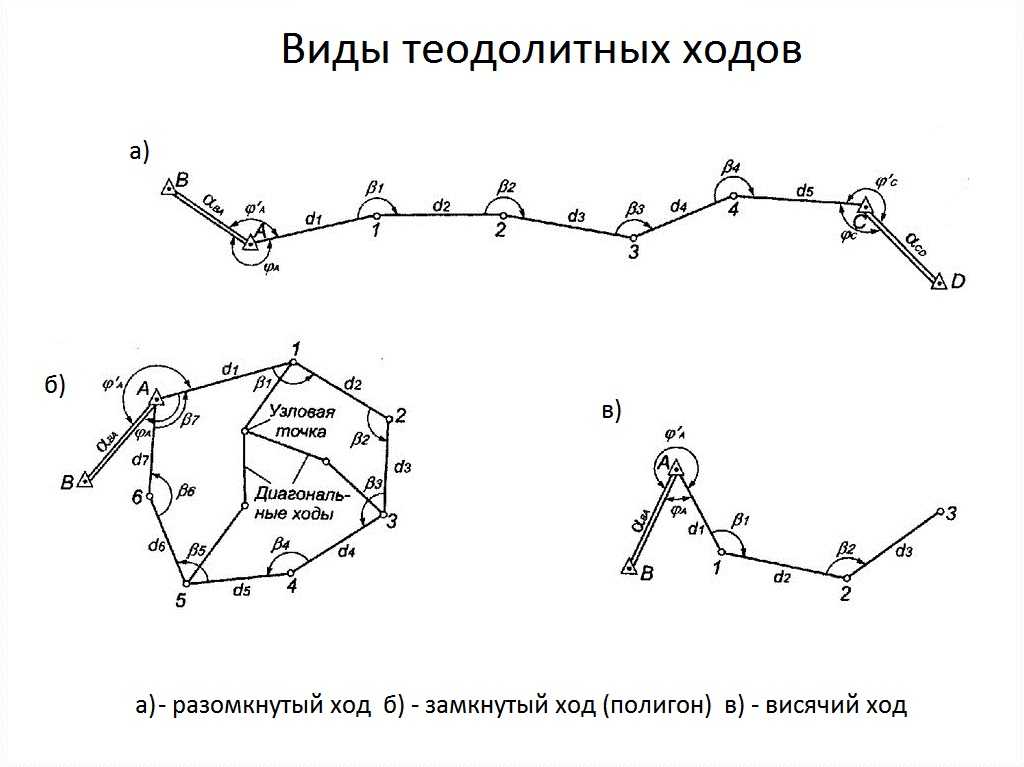
Рисунок 1. Разновидности разомкнутых теодолитных ходов

Нанесение точек теодолитного хода

Когда сетка координат построена, по ней отсчитывают значения для каждой точки и наносят на чертеж с учетом заданного масштаба. Желательно использовать для этих целей хорошо заостренный твердый карандаш. Данные берутся из ведомости координат.

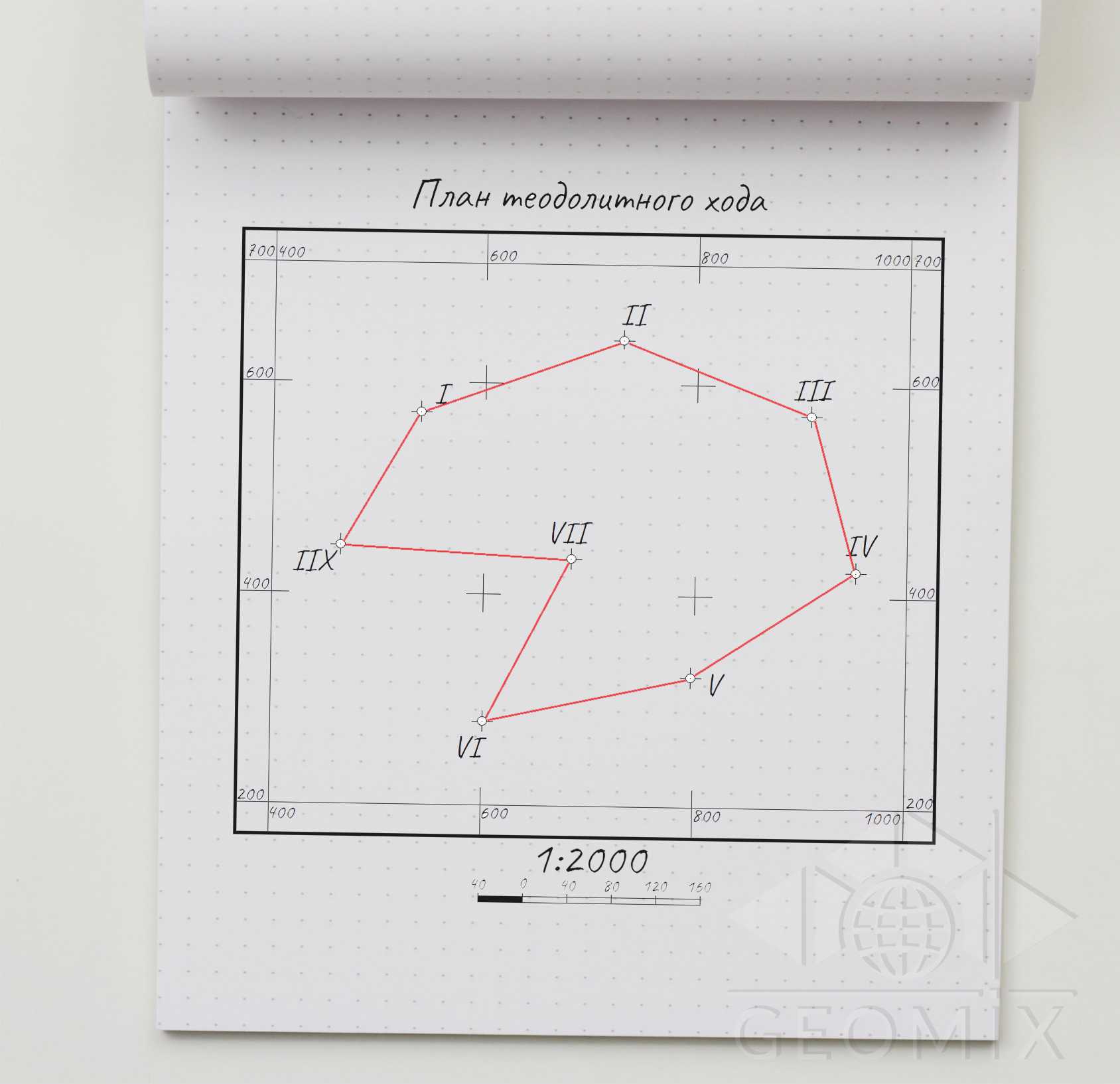
Рисунок 2. Схема теодолитного хода на плане

Лучше для начала определить положение одной или двух точек и проверить правильность их нанесения. Это можно сделать по направлению дирекционного угла, которое должно соответствовать направлению линии на чертеже.

Также необходимо проверить, сходятся ли расстояние между ними с горизонтальным проложением. Допустимая разница не должна превышать 0,2 мм. В случае выявления расхождений необходимо проверить качество координатной сетки и правильность откладывания отрезков.

Схема теодолитного хода

Каждый путь имеет определенную схему, по которой можно определить его вид и назначение, положение. Как говорилось ранее, каждая линия имеет свои отличительные признаки.

Замкнутая схема напоминает собой закрытую фигуру. Для того, чтобы огородить любой участок, нужно именно это построение.

Необходима только одна известная относительная точка, чтобы сделать замкнутое пространство. Так как линия состоит из множества координат, то нахождение углов не является проблемой. Схема напоминает многоугольник.

Висячий ход нужен для тех участков, которые еще находятся в проекте. Эта схема имеет единственную координату, так как конца у нее нет. Конец у данной линии свободен.

Разомкнутый план удобен тем, что координаты известны. Остается только вычислить необходимые углы по координатам.

Начало и конец на данной линии лежат на геодезических обоснованиях. Эта фигура любима многими геодезистами-новичками, которые только пришли в это дело, для них есть допустимая минимальная погрешность.

Подготовка чертежа: построение сетки координат

Перед тем, как нанести на план все его составляющие необходимо должным образом подготовить его. На плотном листе бумаги чертится координатная сетка со сторонами квадратов равными 10 сантиметрам. В работе используют различные инструменты, вроде штангенциркуля, координатографа, линейки Дробышева или обычной масштабной.

Чтобы определить, какое количество квадратов нужно построить для X и Y, используют выражение:

\(N_{X}=(X_{max}-X_{min})/d \)

\(N_{Y}=(Y_{max}-Y_{min})/d \)

Переменные \(X_{max}\) и \(Y_{max}\) – максимальное значение координат с округлением их в большую сторону до кратных длине сетки, а \(X_{min}\) ,\(Y_{min}\) – в меньшую сторону.

\(d \)– длина стороны квадрата на местности (в метрах). Для масштаба 1:1000 это будет 100 метров, а 1:2000 – 200 метров и т.д.

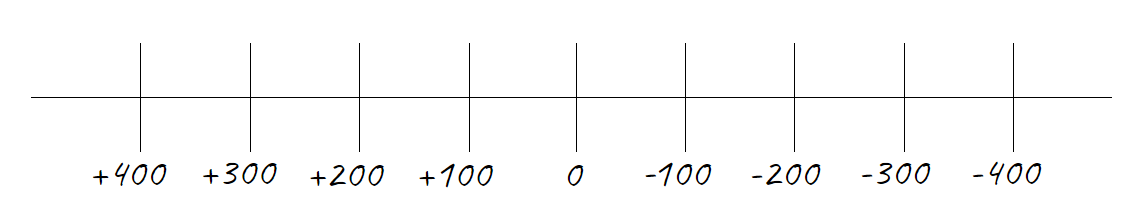
Рисунок 1. Числовая ось сетки координат

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

Максимальные и минимальные значения координат также принято изображать в конце сетки.

Назначение плана теодолитного хода и этапы его составления

Поскольку на небольших территориях искажения измеренных углов и длин будут не столь значительными, их пренебрежение не приведет к значительной потере точности.

Как уже было сказано выше, первостепенная задача этого чертежа – отображение земной поверхности и объектов, которые на ней расположены. Обычно создаются в масштабах 1:500, 1:1000, 1:2000, 1:5000 и 1:10 000.

Принято также различать следующие виды планов:

1. Топографические. Все объекты на местности, включая здания, сооружения, а также растительность и элементы гидрографии должны быть отображены.
2. Ситуационные. Нанесение только наиболее важных и крупных дискретных объектов, расположенных на земной поверхности.
3. Специализированные. Отображение местоположения в пространстве только конкретных элементов. В основном создается для проектирования и последующего строительства сложных инженерных сооружений. Может выполняться в особо крупном масштабе 1:200 и 1:100.

Для составления всех этих графических материалов в основном проводится теодолитная съемка. Сам процесс изготовления плана проводится в такой последовательности:

– создание координатной сетки;

– нанесение точек хода на чертеж;

– отображение ситуации местности.

– оформление.

Решение прямой и обратной геодезической задачи

Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:

\(\Delta X=d\cdot cos \alpha \)

\(\Delta Y=d\cdot sin \alpha \)

где:

Создавайте будущее вместе с нами

Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.

\(d\)–расстояния между соседними пунктами.

\(\alpha \) – значение дирекционного угла.

Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:

\(X_{2}=X_{1}+\Delta X\)

\(Y_{2}=Y_{1}+\Delta Y\)

\(X_{2}=X_{1}+d_{1-2}\cdot cos\alpha _{1-2}\)

\(Y_{2}=Y_{1}+d_{1-2}\cdot sin\alpha _{1-2}\)

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:

\(\Delta X=X_{2}-X_{1}\)

\(\Delta Y=Y_{2}-Y_{1}\)

определяется румб линии \(r_{1-2}\):

\(tgr=\frac{\Delta Y}{\Delta X}\)

из этого выходит, что:

\(r=arctg\frac|{\Delta Y}{\Delta X}|\)

По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:

\(d=\frac{\Delta X}{cos\alpha }\)

\(d=\frac{\Delta Y}{sin\alpha }\)

\(d=\sqrt{\Delta X^2+\Delta Y^2}\)

Схема теодолитного хода

Каждый путь имеет определенную схему, по которой можно определить его вид и назначение, положение. Как говорилось ранее, каждая линия имеет свои отличительные признаки.

Замкнутая схема напоминает собой закрытую фигуру. Для того, чтобы огородить любой участок, нужно именно это построение. 

Необходима только одна известная относительная точка, чтобы сделать замкнутое пространство. Так как линия состоит из множества координат, то нахождение углов не является проблемой. Схема напоминает многоугольник.

Висячий ход нужен для тех участков, которые еще находятся в проекте. Эта схема имеет единственную координату, так как конца у нее нет. Конец у данной линии свободен.

Разомкнутый план удобен тем, что координаты известны. Остается только вычислить необходимые углы по координатам. 

Начало и конец на данной линии лежат на геодезических обоснованиях. Эта фигура любима многими геодезистами-новичками, которые только пришли в это дело, для них есть допустимая минимальная погрешность.

Линейная невязка и невязка приращения значений координат

Несмотря на вышесказанное, случайные погрешности не позволяют алгебраическим суммам выйти в ноль, поэтому они будут равняться другим невязкам приращений координат:

\(f_{x}\sum_{i=1}^{n}\Delta X_{1}\)

\(f_{y}\sum_{i=1}^{n}\Delta Y_{1}\)

Переменные \(f_{x}\) и \(f_{y}\) – проекции линейной невязки \(f_{p}\) на координатной оси, которую можно рассчитать по формуле:

\(f_{p}=\sqrt{f_{x}^{2}+f_{y}^{2}}\)

При этом \(f_{p}\), не должно быть боле, чем 1/2000 от доли периметра полигона, а распределения \(f_{x}\) и \(f_{y}\) проводится следующим образом:

\(\delta X_{i}=-\frac{f_{x}}{P}d_{i} \)

\(\delta Y_{i}=-\frac{f_{y}}{P}d_{i} \)

В этих формулах \(\delta X_{i}\) и \(\delta Y_{i}\) – поправки приращения координат.
і- номера точек;

После приращений и внесения поправок в данные измерений, проводят расчет их исправленных значений.

Исходные данные для расчетов

Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.

По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:

– горизонтальные углы пунктов;

– измеренное расстояние между ними;

– координаты пункта ГГС или опорной сети;

– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.

Общие понятия о системах координат в геодезии

Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.

Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:

1. Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
2. Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.

Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.

Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.

Порядок проведения

Выполнение теодолитного хода начинают с рекогносцировки, подразумевающей изучение ее особенностей и определение наиболее подходящих мест для установки точек.

Расстояние между ними должно варьироваться в пределах от 20 до 350 метров, но оно зависит также и от масштаба съемки. Наилучшей точности можно добиться, если расстояние будет одинаковым, но особенности территории далеко не всегда позволяют это сделать.

Съемку осуществляют на открытом пространстве с хорошей взаимной видимостью между пунктами, закрепленными специальными кольями из дерева, металла и других материалов. Для их долговременной сохранности нередко используются бетонные монолитные столпы. Также рекомендуется привязать каждый знак к твердым объектам поблизости, чтобы можно было восстановить его в случае потери.

Когда все подготовительные процедуры завершены и определено местоположение пунктов начинаются полевые работы. Прибор устанавливают на точке и измеряют угол за один прием, визируясь на соседние, после чего определяют расстояния между ними.

Если строится замкнутый полигон, за начальный берут магнитный азимут одной из сторон. Привязка к пункту геодезической сети необходима для определения дирекционного угла и координат, что позволит обеспечить должный контроль полученных результатов.

Все данные записываются в специальный журнал или автоматически заносятся в память электронного измерительного устройства. В дальнейшем они используются для камеральной обработки, которая подразумевает проведение расчетов с целью вычисления координат пунктов и жестких контуров.

Параллельно со съемкой составляется схематический чертеж, отображающий местоположение объектов на местности, который называется абрисом. Он представляет собой полноценный документ, является неотъемлемой частью технической документации и служит источником информации при построении плана или карты.

Во время снегопада, дождей и других неблагоприятных погодных условий, а также при плохой освещенности, проводить измерения запрещается.

Нанесение ситуации и оформление

Для дальнейших работ применяются абрисы, которые были составлены во время полевой съемки. Чтобы как можно точнее отобразить на плане ситуацию нужно использовать транспортир, прямоугольный треугольник и миллиметровую линейку хорошего качества.

Абрис содержит в себе детальную информацию о местоположении характерных точек жестких контуров местности относительно вершин хода. Выполняется в произвольном масштабе непосредственно во время полевых измерений. Всего различают такие способы съемки ситуации:

1. Перпендикуляров. Местоположение точек определяют длинами перпендикуляров и расстояниями до заданного пункта.
2. Полярных координат. Сторона хода берется за начало координатной оси, а вершина за полюс. Положение точек контуров определяют посредство измерения угла между заданным направлением и расстоянием до них.
3. Биполярных координат (линейная засечка). Измеряются углы между двумя сторонами хода и направлением на заданную точку. Их пересечение и позволит получить ее на чертеже.
4. Створов (промеров). Если ситуация находится на пересечении хода или его сторон проводят линейные промеры. Активно используют для съемки застроенных участков.
5. Обходный способ. Создается дополнительный ход с привязкой к основному.

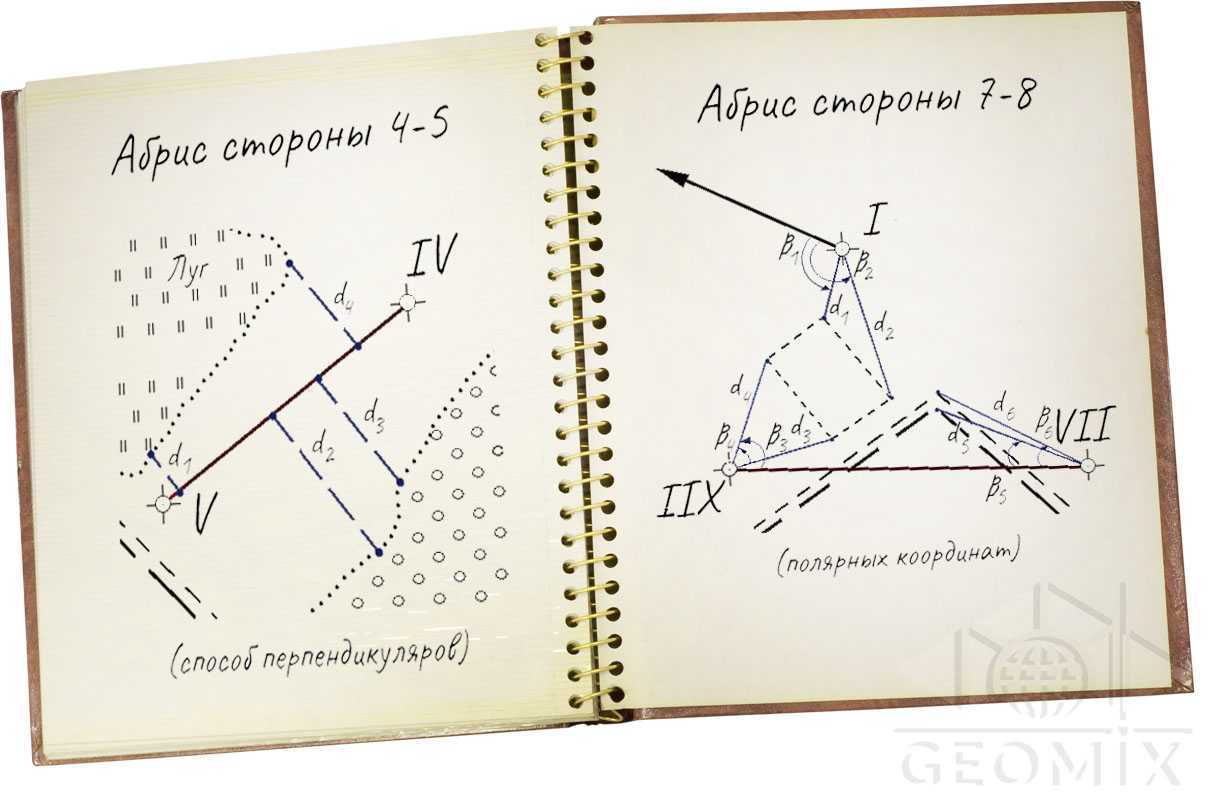
Рисунок 3. Абрис сторон теодолитного хода

При последовательном нанесении контурных точек из абриса на план они будут накладываться друг на друга, формируя местность

Очень важно регулярно проверять их точность, чтобы избежать ошибок

Когда все объекты нанесены карандашом, их вычерчивают тушью, соблюдая правила оформления чертежей. Потом выполняют зарамочное оформление с обязательным указанием названия плана, его масштаба и другой информации.

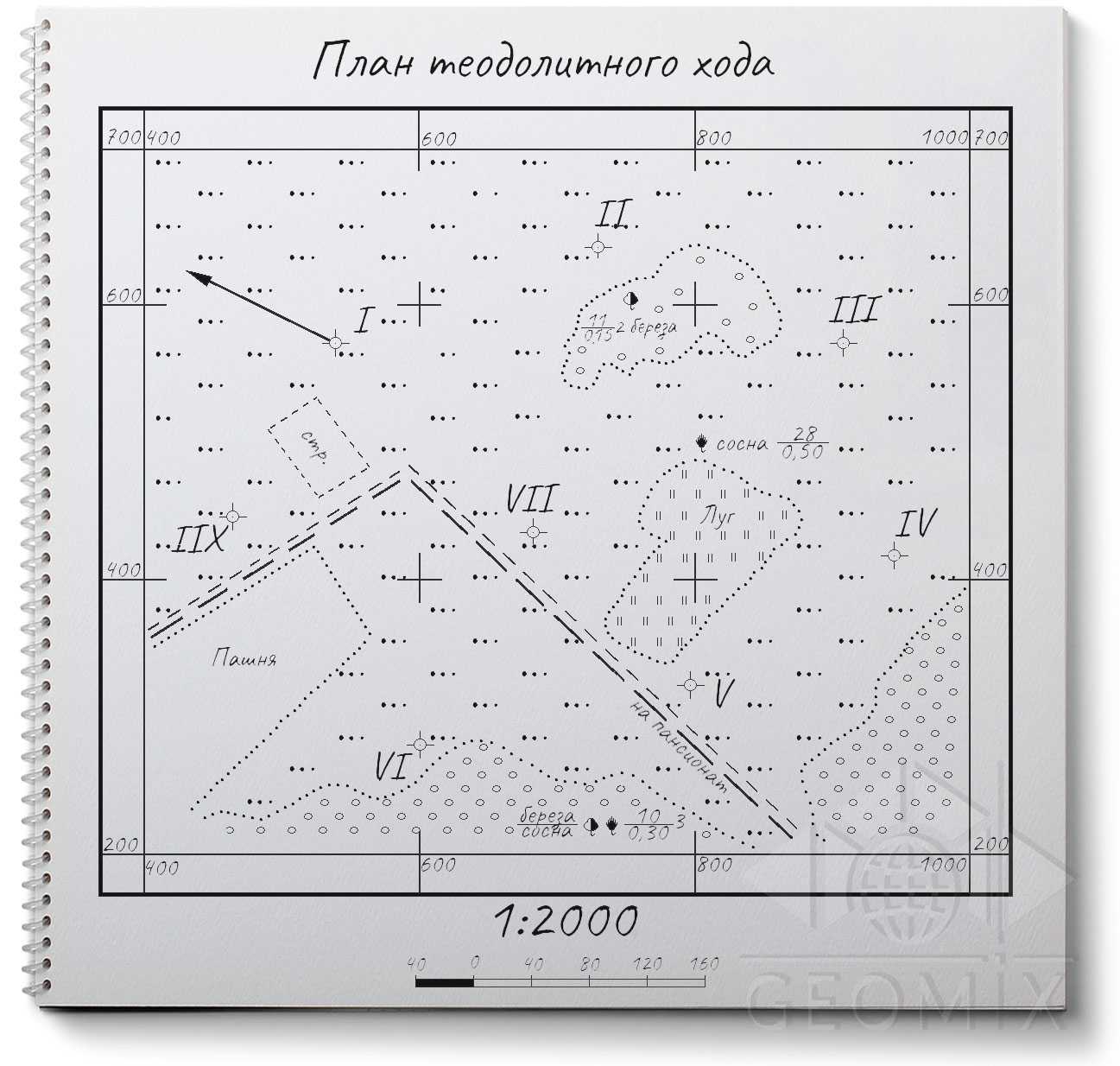
Рисунок 4. Готовый чертеж плана теодолитного хода

Чтобы графически обозначить различные объекты и особенности местности на чертеже используют специальную систему обозначений – условные знаки. После выполнение всех вышеперечисленных процедур процедуру составления плана теодолитного хода можно считать законченной.

Уравнивание

При начале расчетов определяют теоретическую сумму углов , а потом увязывают их, распределяя между ними угловую невязку.

n- количество точек полигона;

\(\sum \beta _\)– значение измеренных угловых величин;

Для получения \(f_\), необходимо рассчитать разность между \(\beta _\), в которой присутствуют погрешности, и \(\sum \beta _\).

В уравнивании \(f_\) выступает как показатель точности проведенных измерительных работ, а ее значение не должно быть выше предельной величины, определяемой из следующей формулы:

t-точность измерительного устройства, n – количество углов. Уравнивание заканчивается равномерным распределением полученной невязки между угловыми величинами.

Основные виды теодолитных ходов

Опытные эксперты выделают несколько типовых схем ломаного построения:

Замкнутый ход представляет собой многоугольную фигуру, которая имеет начало и конец в одной только точке. Само название говорит о построении этой линии. Замкнутая фигура это и есть система такого вида. Чаще всего нужна такая линия для того, чтобы создать контур на любой местности.

Висячий ход используют редко, потому что для его вычисления потребуется специальная формула. Суть его такова, что он имеет только начало в определенной точке координат. Конец нужно вычислять.

Разомкнутый ход можно охарактеризовать как простую линию. Проект трассы или любого другого продолжительного участка невозможен без разомкнутой линии. Опора у нее на известные точки. В отличие от замкнутого, начало и конец располагаются в разных точках.

Основные технические требования к линейным измерениям

Любые геодезические работы должны быть выполнены с четким соблюдением всех правил, дабы обеспечить получение самых точных результатов измерений. Основные требования к данной процедуре изложены в инструкции по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500, а также ряда других нормативных документов.

В зависимости от предельной относительной погрешности  длина теодолитного хода должна соотносится со следующими показателями, приведенными в табл.1.

Таблица 1.

Буровая установка	№ скважины	Литологический тип	Коэф. крепости	Размер отдельности, м	Скорость фактическая, м/c
DM LP	6,0	4,0	2,0	6,0	3,0
СБШ	3,0	2,0	1,0	3,6	1,5
1:1000	1,8	1,2	0,6	1,5	1,5
1:500	0,9	0,6	0,3	—	—

\(m_{s}\) – среднеквадратическая ошибка измеренных расстояний.

Показатели предельно допустимых длин между узловой точкой и исходной уменьшается на 30%, а также должны быть:

– больше 20 м, но меньше 350 м на застроенных участках;

– свыше 40 м и не более 350 м.

Аналогичные требования (табл. 2) есть и к висячим теодолитным ходам:

Таблица 2.

Масштаб	Местность
Застроенная	Не застроенная
1:5000	350	500
1:2000	200	300
1:1000	150	200
1:500	100	150

Измерение длин необходимо проводить в обе стороны и высчитать их среднее значение, а точность приборов должна быть не менее 30”. Допустимое отклонение при центрировании – не более 3 мм.