Search code, repositories, users, issues, pull requests

Уравнивание приращений координат

_______Уравниванием называется совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.

_______
Уравнивание проводится для устранения невязок, обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе уравнвиания это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям).

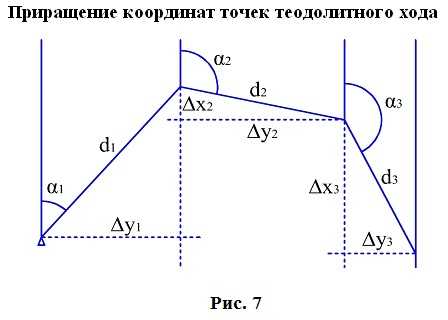
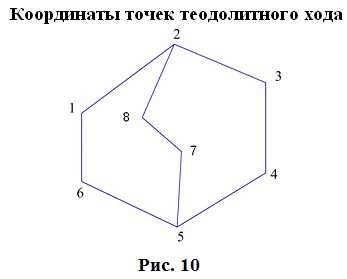
7.1. Вычисление координат точек теодолитного хода

_______
Из решения прямой геодезической задачи по известным длинам сторон и румбам вычисляются приращения координат для каждой стороны хода по формулам:

_______
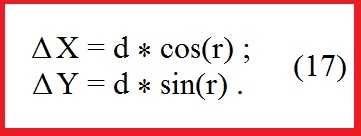Далее вычисляются невязки в приращениях координат замкнутого хода.

7.2. Вычисление невязок в приращениях координат замкнутого хода

_______
Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:

_______
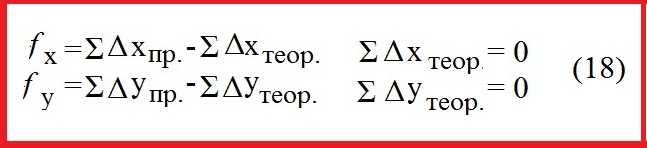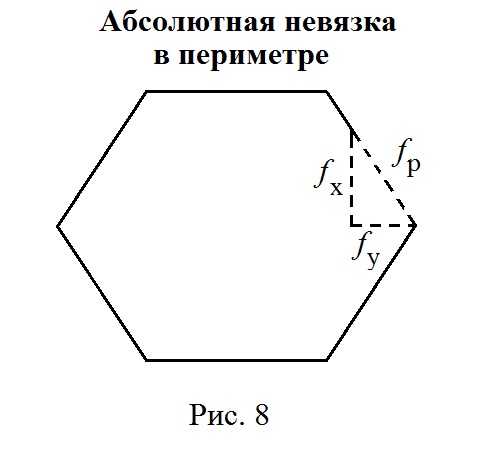
Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину f_р – абсолютная невязка в периметре полигона.

_______

Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий.

_______
Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю.

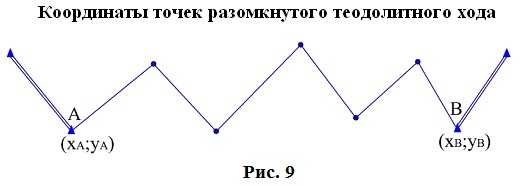
7.3. Вычисление невязок в приращениях координат разомкнутого теодолитного хода

_______
Определение допустимости невязок и их распределения производится так же, как для замкнутого теодолитного хода.

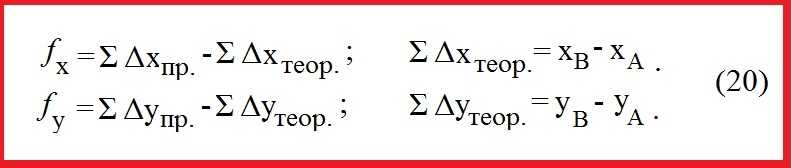например

_______
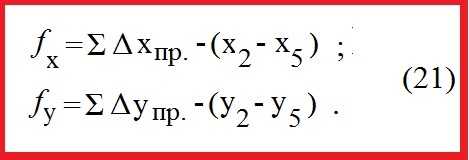По исправленным значениям приращений координат вычисляются координаты всех точек хода по формулам:

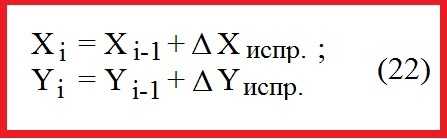Построение плана

_______
Построение плана выполняются в следующей последовательности:1) построение координатной сетки,2) нанесение вершин теодолитного хода по координатам,3) нанесение на план контуров местности,4) оформление плана.

8.1. Построение координатной сетки

_______
Координатная сетка строится обычно со стороной 10х10 см.
Используется два способа:

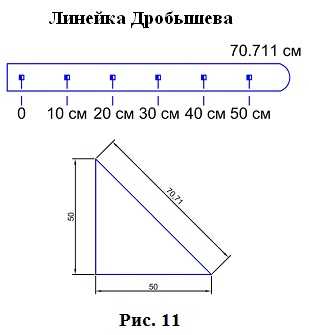
_______1) построение сетки с помощью линейки Дробышева:

_______
Построение сетки основано на построении прямоугольного треугольника с катетами 50×50 см и гипотенузой 70,711 см;

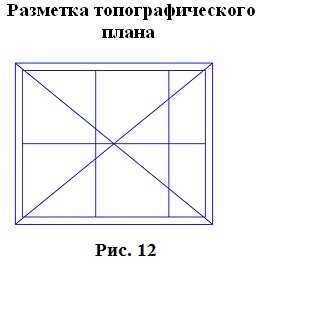
2) построение сетки с помощью циркуля, измерителя и масштабной линейки:

_______
Этот способ применяется при размере плана меньше, чем 50 см. Сетка контролируется путем сравнения длин сторон или диагоналей квадратов. Допустимое отклонение – 0,2 мм. Построенную сетку подписывают координатами так, чтобы участок поместился.

_______
Вершины теодолитного хода наносятся на план по координатам относительно сетки с помощью измерителя и поперечного масштаба.

_______
Контроль правильности построения точек выполняется по известным расстояниям между точками. Допустимое расхождение – 0,3 мм в масштабе плана.

_______
Например: 1:2000 – 0,6 м.

_______
Контуры местности наносятся на план в соответствии с абрисами.

_______
Оформление плана выполняется в строгом соответствии с условными знаками, установленными для данного масштаба.

Инструкция по прохождению теста

• Выберите один из вариантов в каждом из 10 вопросов;
• Нажмите на кнопку «Показать результат»;
• Скрипт не покажет результат, пока Вы не ответите на все вопросы;
• Загляните в окно рядом с номером задания. Если ответ правильный, то там (+). Если Вы ошиблись, там (-).
• За каждый правильный ответ начисляется 1 балл;
• Оценки: менее 5 баллов — НЕУДОВЛЕТВОРИТЕЛЬНО, от 5 но менее 7.5 — УДОВЛЕТВОРИТЕЛЬНО, 7.5 и менее 10 — ХОРОШО, 10 — ОТЛИЧНО;
• Чтобы сбросить результат тестирования, нажать кнопку «Сбросить ответы»;

[править] Пример программной реализации

Исходники вышеприведённых функций можно найти в архиве Sph.zip в файле sph.c. Кроме того, в файл sph.h включены следующие определения:

#define A_E 6371.0				// радиус Земли в километрах
#define Degrees(x) (x * 57.29577951308232)	// радианы -> градусы
#define Radians(x) (x / 57.29577951308232)	// градусы -> радианы

Теперь напишем программу, которая обращается к функции SphereInverse для решения обратной задачи:

#include <stdio.h>
#include <stdlib.h>
#include "sph.h"
 
int main(int argc, char *argv)
{
  char buf1024;
  double pt12, pt22;
  double lat1, lon1, lat2, lon2, azi1, azi2, dist;
 
  while (fgets(buf, 1024, stdin) != NULL) {
    sscanf(buf, "%lf %lf %lf %lf", &lat1, &lon1, &lat2, &lon2);
    pt1 = Radians(lat1);
    pt11 = Radians(lon1);
    pt2 = Radians(lat2);
    pt21 = Radians(lon2);
    SphereInverse(pt2, pt1, &azi2, &dist);		// Решение обратной задачи
    SphereInverse(pt1, pt2, &azi1, &dist);		// Вычисление обратного азимута
    printf("%f\t%f\t%.4f\n", Degrees(azi1), Degrees(azi2), dist * A_E);
  }
  return ;
}

В архиве Sph.zip этот код находится в файле inv.c. Создадим исполняемый модуль inv компилятором gcc:

$ gcc -o inv inv.c sph.c -lm

Впрочем, в архиве есть Makefile. Для MS Windows готовую программу inv.exe можно найти в архиве Sph-win32.zip.

Программа читает данные из стандартного ввода консоли и отправляет результаты на стандартный вывод. Для чтения и записи файлов используются символы перенаправления потока «>» и «<» соответственно. Из каждой строки ввода программа считывает координаты двух точек φ₁, λ₁, φ₂, λ₂, которые должны быть в градусах, решает обратную задачу и записывает в строку вывода α₁, α₂, s (азимуты прямого и обратного направлений в градусах; расстояние между пунктами в километрах, а точнее, в единицах, определённых константой A_E).

Создадим файл inv.dat, содержащий одну строку данных:

30 0 52 54

После запуска программы

$ inv < inv.dat

получим α₁, α₂, s:

44.804060 262.415109 5001.1309

В архиве Sph-py.zip находятся скрипты на языке Питон. Выполнение скрипта в командной консоли:

$ python inv.py inv.dat

Примеры

Решение прямой геодезической задачи

Для решения прямой геодезической задачи, неоходимо создать объект класса .

var directEllipsoid = new DirectProblemService(new Ellipsoid());
var directSpheroid = new DirectProblemService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для решения прямой задачи вызвать метод , в который передать в качестве параметров, начальную точку, азимут = направление и расстояние:

var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N);
var azimuth = 21;
var distance = 2000;
var directAnswer = directEllipsoid.DirectProblem(point1, azimuth, distance);

Ответ содержит вторую точку ортодромии и обратный азимут .

Решение обратной геодезической задачи

Для решения обратной геодезической задачи, неоходимо создать объект класса .

var inverseEllipsoid = new InverseProblemService(new Ellipsoid());
var inverseSpheroid = new InverseProblemService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для решения обратной задачи вызвать метод , в который передать в качестве параметров, две точки:

var point1 = new Point(15, 25, 53, CardinalLongitude.W, 28, 7, 38, CardinalLatitude.N);
var point2 = new Point(59, 36, 30, CardinalLongitude.W, 13, 5, 46, CardinalLatitude.N);
var inverseAnswer = inverseEllipsoid.OrthodromicDistance(point1, point2);

Ответ содержит прямой и обратный азимуты , , а также расстояние между точками .

Вычисление точки пересечения ортодромий

Для вычисления точки пересечения ортодромий, неоходимо создать объект класса .

var intersectEllipsoid = new IntersectService(new Ellipsoid());
var intersectSpheroid = new IntersectService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для рассчёта вызвать метод , в который передать в качестве параметров, по две точки для каждой из двух ортодромий:

var point1 = new Point(22, 36, 30, CardinalLongitude.E, 13, 5, 46, CardinalLatitude.N);
var point2 = new Point(27, 25, 53, CardinalLongitude.E, 15, 7, 38, CardinalLatitude.N);
var point3 = new Point(20, 36, 30, CardinalLongitude.E, 17, 5, 46, CardinalLatitude.N);
var point4 = new Point(26, 25, 53, CardinalLongitude.E, 13, 7, 38, CardinalLatitude.N);
var intersectCoord = intersectEllipsoid.IntersectOrthodromic(point1, point2, point3, point4);

Ответом будет точка — объект класса , в котором определены долгота и широта, в десятичных градуса (,) или в радианах (,).

Вычисление широты по долготе или долготы по широте

Для рассчётов, неоходимо создать объект класса .

var intermediateEllipsoid = new IntermediatePointService(new Ellipsoid());
var ntermediateSpheroid = new IntermediatePointService(new Spheroid());

В качестве параметра в конструктор следует передать объект реализующий интерфейс , в котором задаются полярный и экваториальный радиус, а так же коэффициент полярного сжатия.

Для вычисления широты вызвать метод , в который передать значение долготы, для которого мы вычисляем широту, и две координаты характеризующие ортодромию.

var coord1 = new Point(10, 10);
var coord2 = new Point(30, 50);
var lat = intermediateEllipsoid.GetLatitude(20, coord1, coord2);

Для вычисления долготы вызвать метод , в который передать значение широты, для которого мы вычисляем долготу, и две координаты характеризующие ортодромию.

var coord1 = new Point(10, 10);
var coord2 = new Point(30, 50);
var lat = intermediateEllipsoid.GetLongitude(20, coord1, coord2);

В обоих случая ответом будет значение типа .

[править] Алгоритм

Существует великое множество подходов к решению поставленной задачи. Рассмотрим простой и надёжный векторный метод.

Последовательность решения:

1. преобразовать углы (90° − σ) и (180° − α₁) в декартовы координаты,
2. развернуть координатные оси вокруг оси Y на угол (φ₁ − 90°),
3. развернуть координатные оси вокруг оси Z на угол −λ₁,
4. преобразовать декартовы координаты в сферические.

Если третий пункт пропустить, на выходе вместо долготы λ₂ получится разность долгот (λ₂ − λ₁), что упростит алгоритм. Останется только прибавить долготу первого пункта. С другой строны, благодаря третьему пункту долгота λ₂ всегда будет в диапазоне .

Пример реализации алгоритма в виде функции языка Си:

/*
 * Решение прямой геодезической задачи
 *
 * Аргументы исходные:
 *     pt1  - {широта, долгота} точки Q1
 *     azi  - азимут начального направления
 *     dist - расстояние (сферическое)
 *
 * Аргументы определяемые:
 *     pt2  - {широта, долгота} точки Q2
 */
void SphereDirect(double pt1, double azi, double dist, double pt2)
{
  double pt2, x3;
 
  pt = M_PI_2 - dist;
  pt1 = M_PI - azi;
  SpherToCart(pt, x);			// сферические -> декартовы
  Rotate(x, pt1 - M_PI_2, 1);	// первое вращение
  Rotate(x, -pt11, 2);		// второе вращение
  CartToSpher(x, pt2);	     		// декартовы -> сферические
 
  return;
}

Следует заметить, что прямая и обратная задача математически идентичны, и алгоритмы их решения зеркально отражают друг друга.

Преобразование сферических координат в декартовы

В данном случае в качестве сферических координат φ, λ подставим углы (90° − σ), (180° − α₁).

Реализация на Си:

/*
 * Преобразование сферических координат в вектор
 *
 * Аргументы исходные:
 *     y - {широта, долгота}
 *
 * Аргументы определяемые:
 *     x - вектор {x, y, z}
 */
void SpherToCart(double y, double x)
{
  double p;
 
  p = cos(y);
  x2 = sin(y);
  x1 = p * sin(y1);
  x = p * cos(y1);
 
  return;
}

Вращение вокруг оси

Представим оператор вращения вокруг оси X на угол θ в следующем виде:

Операторы вращения вокруг осей Y и Z получаются перестановкой символов.

Реализация вращения вокруг i-ой координатной оси на Си:

/*
 * Вращение вокруг координатной оси
 *
 * Аргументы:
 *     x - входной/выходной 3-вектор
 *     a - угол вращения
 *     i - номер координатной оси (0..2)
 */
void Rotate(double x, double a, int i)
{
  double c, s, xj;
  int j, k;
 
  j = (i + 1) % 3;
  k = (i - 1) % 3;
  c = cos(a);
  s = sin(a);
  xj = xj * c + xk * s;
  xk = -xj * s + xk * c;
  xj = xj;
 
  return;
}

Преобразование декартовых координат в сферические

В данном случае в роли сферических координат φ, λ окажутся φ₂, λ₂.

Реализация на Си:

/*
 * Преобразование вектора в сферические координаты
 *
 * Аргументы исходные:
 *     x - {x, y, z}
 *
 * Аргументы определяемые:
 *     y - {широта, долгота}
 *
 * Возвращает:
 *     длину вектора
 */
double CartToSpher(double x, double y)
{
  double p;
 
  p = hypot(x, x1);
  y1 = atan2(x1, x);
  y = atan2(x2, p);
 
  return hypot(p, x2);
}

[править] Общие положения

В качестве модели Земли принимается сфера с радиусом R, равным среднему радиусу земного эллипсоида. Аналогом прямой линии на плоскости является геодезическая линия на поверхности. На сфере геодезическая линия — дуга большого круга.

Введём следующие обозначения:

• φ — географическая широта,
• λ — географическая долгота,
• α — азимут дуги большого круга,
• σ — сферическое расстояние (длина дуги большого круга, выраженная в долях радиуса шара).

Линейное расстояние по дуге большого круга s связано со сферическим расстоянием σ формулой s = R σ.

Прямая и обратная геодезические задачи являются важными элементами более сложных геодезических задач.