Общие сведения
Функцией называется зависимость одной переменной от другой. Если записать ее в виде равенства w = f (p), то величина «w» зависит от «р». Первая называется значением функциональной зависимости, а вторая — ее аргументом. Последний может принимать любые значения, кроме превращающих «w» в пустое множество. Примером является выражение w = / (p 2 — 1). При значениях р1 = -1 и р2 = 1 получается пустое множество, поскольку на нуль делить нельзя.

Когда математики говорят, что нужно произвести исследование функции на непрерывность, т. е. необходимо найти точки разрыва первого и второго рода. Если же таковых нет, то данное утверждение следует доказать математическим методом.
Непрерывной называется функция, которая не имеет точек разрыва, и меняется без существенных скачков в некоторых точках или промежутках, т. е. обладает определенным знакопостоянством. Это свойство определяется при помощи метода, представляющего совокупность математических преобразований. Последние основываются на теоремах. Они позволяют доказать существование или отсутствие точек и интервалов разрыва графика функции.
Классификация точек разрыва
Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа и слева.
Если, кроме этого, выполняется хотя бы одно из условий то функция в точке х = а имеет неустранимый разрыв первого рода.
Если пределы равны, однако функция не существует то имеем устранимый разрыв первого рода.
Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа или слева не существует или бесконечна.
Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ если они разные и не равны бесконечности.
При нахождении точек разрыва функции можно руководствоваться следующими правилами:
1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале. 2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки. 3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена. Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.
Рассмотрим несколько задач по данной теме.
Задача 1.Найти точки разрыва функции а)
Решение: Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая
Найдем односторонние пределы в точках разрыва
При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.
Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы являются точками разрыва второго рода. График функции приведен на рисунке ниже
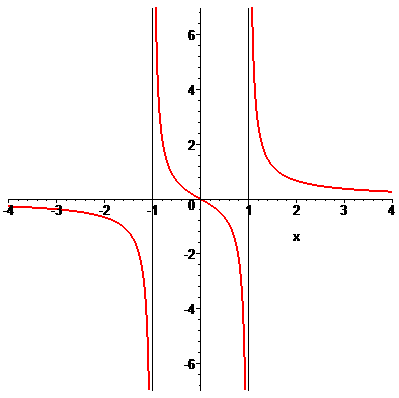
——————————————————-
б)
Решение: Задача достаточно простая. В первую очередь находим нули знаменателя
Таким образом функция определена на всей действительной оси за исключением точек , которые являются точками разрыва. Вычислим односторонние пределы справа и слева
Пределы бесконечны поэтому, по определению, имеем точки разрыва второго рода.
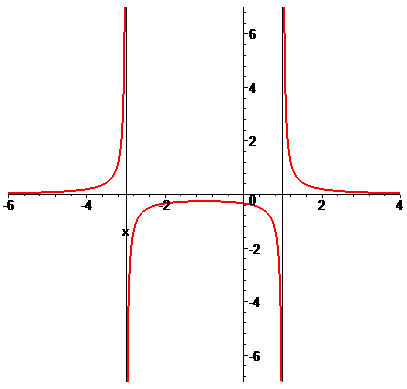
Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.
——————————————————-
в)
Решение: Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке![]()
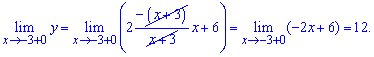
Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.
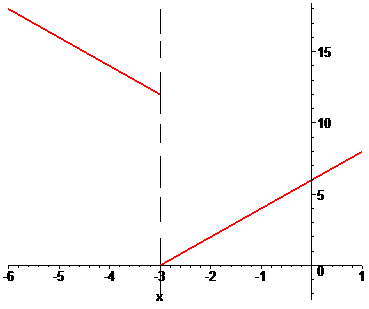
——————————————————-
Задача 2.Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.
а)
Решение: Для заданной функции точка x = 2 является точкой разрыва. Найдем предел функции , чтобы определить характер разрыва![]()
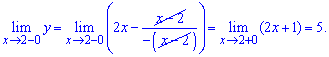
По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2
График функции на интервале который нас интересует приведен далее
——————————————————-
б)
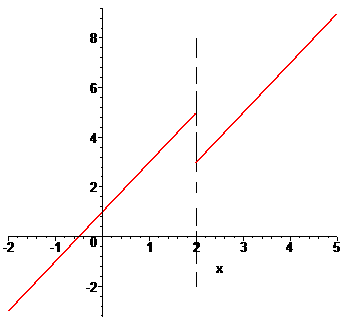
Решение: Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы
Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция — непрерывная.
Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.
Исследуем на непрерывность вторую точку
По определению функция в точке x = 2 имеет неустранимый разрыв І рода.
Прыжок функции равен 29 — (- 3) = 31.
По условию задания построим график функции.
Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.
Свойства функций, непрерывных в точке.
Локальные свойства непрерывной функции.
Свойство 1
Если функция \(f\) непрерывна в точке \(a\), то она ограничена в некоторой окрестности этой точки, то есть
$$
\exists\delta>0\quad\exists C>0:\;\forall x\in U_{\delta}(a)\rightarrow|f(x)|\leq C\nonumber
$$
Свойство 2
Если функция \(f\) непрерывна в точке \(a\), причем \(f(a)\neq 0\), то в некоторой окрестности точки \(a\) знак функции совпадает со знаком числа \(f(a)\), то есть
$$
\exists\delta>0:\quad\forall x\in U_{\delta}(a)\rightarrow \operatorname{sign}\ f(x)=\operatorname{sign}\ f(a).\nonumber
$$
\(\circ\) Эти утверждения следуют из . \(\bullet\)
Непрерывность суммы, произведения и частного.
Свойство 3
Если функции \(f\) и \(g\) непрерывны в точке \(a\), то функции \(f+g\), \(fg\) и \(f/g\) (при условии \(g(a)\neq 0\)) непрерывны в точке \(a\).
\(\circ\) Это утверждение следует из определения непрерывности и . \(\bullet\)
Непрерывность сложной функции.
Напомним, что такое сложная функция.
Пусть функции \(y=\varphi(x)\) и \(z=f(y)\) определены на множествах \(X\) и \(Y\) соответственно, причем множество значений функции \(\varphi\) содержится в области определения функции \(f\). Тогда функция, которая принимает при каждом \(x\in X\) значение \(F(x)=f(\varphi(x))\), называется сложной функцией или суперпозицией (композицией) функций \(\varphi\) и \(f\).
Теорема 2
Если функция \(z=f(y)\) непрерывна в точке \(y_0\), а функция \(y=\varphi(x)\) непрерывна в точке \(x_0\), причем \(y_0=\varphi(x_0)\), то в некоторой окрестности точки \(x_0\) определена сложная функция \(f(\varphi(x_0))\), и эта функция непрерывна в точке \(x_0\).
\(\circ\) Пусть задано произвольное число \(\varepsilon>0\). В силу непрерывности функции \(f\) в точке \(y_0\) существует число \(\rho=\rho(\varepsilon)>0\) такое, что \(U_\rho(y_0)\subset D(f)\) и
$$
\forall y\in U_\rho(y_0)\rightarrow f(y)\in U_{\varepsilon}(z_{0}),\label{ref2}
$$
где \(z_{0}=f(y_{0})\).
В силу непрерывности функции \(\varphi\) в точке \(x_{0}\) для найденного в \eqref{ref2} числа \(\rho>0\) можно указать число \(\delta=\delta_{\rho}=\delta(\varepsilon)>0\) такое, что
$$
\forall x\in U_\delta(x_0)\rightarrow \phi (x)\in U_\rho (y_0).\label{ref2′}
$$
Из условий \eqref{ref2} и \eqref{ref2′} следует, что на множестве \(U_\delta(x_0)\) определена сложная функция \(f(\varphi(x))\), причем
$$
\forall x\in U_\delta(x_0)\rightarrow f(y)=f(\varphi(x))\in U_{\varepsilon}(z_{0}),\nonumber
$$
где \(z_0=f(\varphi(x_0))=f(y_{0})\), то есть
$$
\forall \varepsilon>0\;\exists \delta>0:\quad \forall х\in U_\delta(x_0)\rightarrow f(\varphi(х))\in U_\varepsilon(\varphi(x_0)).\nonumber
$$
Это означает, в силу определения непрерывности, что функция \(f(\varphi(x))\) непрерывна в точке \(x_0\). \(\bullet\)
Замечание 2
Соответствие между окрестностями точек \(x_0,\ y_0,\ z_0\) представлено на рис. 11.1. По заданному числу \(\varepsilon>0\) сначала находим \(\rho>0\), а затем для чисел \(\rho>0\) находим \(\delta>0\).
Рис. 11.1
Интуитивное определение непрерывности
Большинство студентов, когда слышат термин «непрерывная функция», представляют себе линию, которую можно начертить, не отрывая карандаша от бумаги. Например, обычную параболу:
Или просто какую-нибудь плавную кривую:
Главное, чтобы у этих линий не было никаких особенностей. Они не «разваливаются» на куски, не «улетают» в бесконечность рядом с какой-то точкой, и вообще для любого $x$ мы прямо по графику можем определить, чему будет равен $y$.
Другое дело — функции с нарушением непрерывности. Или, как говорят, с точками разрыва. Обычно студенты сразу называют функцию $y={1}/{{{x}^{2}}}\;$ — классическую гиперболу, которая не определена в точке $x=0$, а график «улетает» в бесконечность в окрестности этой точки:
Впрочем, для возникновения разрыва функции вовсе не обязательно уходить куда-то в бесконечность. Достаточно просто иметь выколотую точку. Взгляните:
Перед нами всё та же парабола $y={{x}^{2}}$, но с выколотой точкой $x=-2$. Как такое возможно? Очень просто. Например, именно так выглядит график функции
\
Значение этой функции не определено при $x=-2$, поскольку знаменатель дроби обращается в ноль. Но во всех остальных точках знаменатель $x+2\ne 0$, и можно выполнить сокращение:
\
И это не какая-то «искусственная» задача — такие функции регулярно встречаются на ОГЭ и ЕГЭ по математике, особенно в задачах с параметром.
Но и это ещё не всё. Функция может быть определена на всей числовой прямой — и всё равно иметь точку разрыва:
Это график кусочно-заданной функции
\
Она определена для всех $x\in \mathbb{R}$, в т.ч. при $x=0$. Однако именно в точке $x=0$ происходит скачкообразное изменение: $f\left( 0 \right)=0$, но малейший шаг влево — и вот уже $f\left( x \right)=-1$. А малейший шаг вправо — и $f\left( x \right)=1$.
Итого проблемы возникают там, где функция «улетает» в бесконечность, либо меняется скачкообразно, либо вообще не определена. И тут мы переходим к строгому определению непрерывности.
Что такое непрерывное изменение функции?
Непрерывное изменение функции
можно определить как изменение постепенное, без скачков, при котором малое изменение
аргумента
влечёт малое изменение функции .
Проиллюстрируем это непрерывное изменение функции на примере.
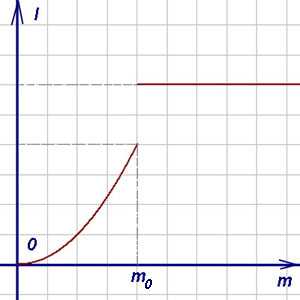
Пусть над столом висит на нитке груз. Под действием этого груза нитка
растягивается, поэтому расстояние груза от точки
подвеса нити является функцией массы груза ,
то есть ,
.
Если немного изменить массу груза, то расстояние
изменится мало: малым изменениям
соответствуют малые изменения . Однако если масса
груза близка к пределу прочности
нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние
скачкообразно увеличится и станет равным расстоянию
от точки подвеса до поверхности стола. График функции
изображён на рисунке. На участке
этот график является непрерывной (сплошной) линией, а в точке
он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках,
кроме , функция
непрерывна,
а в точке
она имеет разрыв.
Исследование функции на непрерывность может быть как
самостоятельной задачей, так и одним из этапов полного исследования функции и построения
её графика.
Непрерывность функции на промежутке
Пусть функция
определена в интервале
и непрерывна в каждой точке этого интервала. Тогда она называется непрерывной в
интервале . Аналогично
определяется понятие непрерывности функции на промежутках вида
,
,
.
Пусть теперь функция
определена на отрезке .
Разница между интервалом и отрезком: граничные точки интервала не входят в интервал,
а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой
односторонней непрерывности: в точке a, оставаясь на отрезке ,
мы можем приближаться только справа, а к точке b —
только слева. Функция называется непрерывной на отрезке ,
если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке
a и непрерывна слева в точке b.
Примером непрерывной функции может служить любая из элементарных функций.
Каждая элементарная функция непрерывна на любом отрезке, на котором она определена.
Например, функции и
непрерывны
на любом отрезке , функция
непрерывна
на отрезке , функция
непрерывна
на любом отрезке, не содержащем точку .
Пример 4. Исследовать функцию
на непрерывность.
Решение. Проверяем первое условие. Функция не определена в точках
— 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой
не выполняется. Поэтому данная функция является непрерывной на интервалах
.
Пример 5. Определить, при каком значении
параметра a непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Найдём правосторонний предел при :
.
Очевидно, что значение
в точке должно быть
равно :
Ответ: функция непрерывна на всей области определения при
.
Пример 6. Определить, при каких значениях
параметров a и b непрерывна на всей области определения функция
Решение.
Найдём левосторонний предел функции в точке :
.
Следовательно, значение
в точке
должно быть равно 1:
.
Найдём левосторонний функции в точке :
.
Очевидно, что значение функции в точке
должно быть равно :
Ответ: функция непрерывна на всей области определения при
.
Понятие непрерывности функции.
Определение 1
Функция \(f(x)\), определенная в некоторой окрестности точки \(a\), называется непрерывной в точке \(a\), если
$$
\displaystyle \lim_{x\rightarrow a}f(x)=f(a)\label{ref1}
$$
Таким образом, функция \(f\) непрерывна в точке \(a\), если выполнены следующие условия:
- функция \(f\) определена в некоторой окрестности точки \(a\), то есть существует число \(\delta_0>0\) такое, что \(U_{\delta_{0}}(a)\subset D(f)\);
- существует \(\displaystyle \lim_{x\rightarrow a}f(x)=A\);
- \(A=f(a)\).
Определение непрерывности функции \(f(x)\) в точке \(a\), выраженное условием \eqref{ref1}, можно сформулировать с помощью неравенств (на языке \(\varepsilon-\delta\)), с помощью окрестностей и в терминах последовательностей соответственно в виде
- \(\forall \varepsilon>0\ \exists\delta>0:\quad\forall x:|x-a| < \delta\rightarrow|f(x)-f(a)| < \varepsilon,\)
- \(\forall \varepsilon>0\ \exists\delta>0:\quad\forall x\in U_{\delta}(a)\rightarrow f(x)\in U_{\varepsilon}(f(a)),\)
- \(\displaystyle\forall\{x_{n}\}:\ \lim_{n\rightarrow\infty}x_{n}=a\rightarrow\lim_{n\rightarrow\infty}f(x_{n})=f(a).\)
Назовем разность \(x-a\) приращением аргумента и обозначим \(\Delta x\), а разность \(f(x)-f(a)\) — приращением функции, соответствующим данному приращению аргумента \(\Delta x\), и обозначим \(\Delta y\). Таким образом,
$$
\Delta x=x-a,\;\Delta y=f(x)-f(a)=f(a+\Delta x)-f(a).\nonumber
$$
При этих обозначениях равенство \eqref{ref1} примет вид
$$
\lim_{\Delta x\rightarrow 0}\Delta y=0.\nonumber
$$
Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Пример 1
Показать, что функция \(f(x)\) непрерывна в точке \(a\), если:
- \(f(x)=x^3, a=1\);
- \(f(x)=\displaystyle \frac{1}{x^{2}}, a\neq 0\);
- \(f(x)=\sqrt{x}, a>0\);
- \(f(x)=\displaystyle \left\{\begin{array}{lc}x\sin\frac1x,&x\neq0,\\0,&x=0,\end{array}\right.a=0\)
- \(\triangle\)Если \(x\rightarrow 1\), то по свойствам пределов (\S 10, (11)) получаем \(x^3\rightarrow 1\), то есть для функции \(f(x)=x^3\) в точке \(x=1\) выполняется условие \eqref{ref1}. Поэтому функция \(x^3\) непрерывна в точке \(x=1\).
- Если \(x\rightarrow a\), где \(a\neq 0\), то, используя свойства пределов (\S 10), получаем \(\displaystyle \frac{1}{x}\rightarrow\frac{1}{a},\;\displaystyle \frac{1}{x^{2}}\rightarrow\frac{1}{a^{2}}\), то есть Функция \(\displaystyle \frac{1}{x^{2}}\) непрерывна в точке \(x=a,\;(a\neq 0)\).
- Так как \(\displaystyle |\sqrt{x}-\sqrt{a}|=\frac{|x-a|}{\sqrt{x}+\sqrt{a}}\), то отсюда получаем \(0\leq|\sqrt{x}-\sqrt{a}|\;<\;\displaystyle\frac{|x-a|}{\sqrt{a}}\). Следовательно, \(\sqrt{x}-\sqrt{a}\rightarrow 0\) при \(x\rightarrow a\). Это означает, что функция \(\sqrt{x}\) непрерывна в точке \(a\), где \(a>0\).
- Функция \(f\) определена на \(\mathbb{R}\), и при любом \(x\in\mathbb{R}\) выполняется неравенство \(0\leq|f(x)-f(0)|=|f(x)|\leq|x|\), так как \(\left|\sin{\frac{1}{x}}\right|\leq1\) при \(x\neq 0\). Следовательно, \(\displaystyle \lim_{x\rightarrow 0}f(x)=f(0)=0\), то есть функция \(f\) непрерывна в точке \(x=0.\quad\blacktriangle\)
По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция \(f\) определена на полуинтервале \((a-\delta,a]\) и \(\displaystyle \lim_{x\rightarrow a-0}f(x)=f(a)\), то есть\(f(a-0)=f(a)\), то эту функцию называют непрерывной слева в точке \(a\).
Аналогично, если функция \(f\) определена на полуинтервале \([a,a+\delta)\) и \(f(a+0)=f(a)\), то эту функцию называют непрерывной справа в точке \(a\).
Например, функция \(f(x)=\) непрерывна справа в точке \(x=1\) и не является непрерывной слева в этой точке, так как \(f(1-0)=0,\;f(1+0)=f(1)=1\).
Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.






























