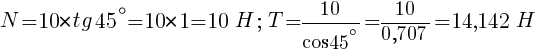Системы сил
Система сил – это совокупность нескольких сил, действующих на данное тело или систему тел.
Эквивалентные системы сил – это системы сил, под действием которых твердое тело находится в одинаковых .
Равнодействующая сила – это сила, эквивалентная некоторой системе сил.
Система взаимно уравновешивающихся сил – это система сил, которая не меняет тела.
Внешние силы, действующие на механическую систему – это силы, действующие на тела рассматриваемой системы со стороны тел, не входящих в эту систему.
Внутренние силы, действующие на механическую систему – это силы, действующие на тела рассматриваемой системы со стороны тел, входящих в эту систему.
Например, если в качестве механической системы мы возьмем стол с лежащей на нем книгой, то силы тяжести, действующие на оба тела и сила давления поверхности пола на стол, являются внешними силами. А сила давления книги на стол и сила давления стола на книгу будут внутренними.
Использованная литература: А. А. Яблонский, В.М. Никифорова, Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
Определение статики
Статика – это раздел теоретической механики, в котором изучаются условия равновесия материальных тел, находящихся под действием сил, а также методы преобразования сил в эквивалентные системы для упрощения расчетов.
Собственно условия равновесия твердого тела представляют собой систему векторных уравнений: векторная сумма сил, приложенных к телу равна нулю:(1) ; векторная сумма моментов этих сил относительно произвольного неподвижного центра равна нулю:(2) . Нередко приложенные к телу силы распределены таким образом, что исследование этих уравнений представляет собой довольно громоздкую задачу. Например силы, возникающие в следствие земного притяжения, распределены по всем точкам тела пропорционально их массам. Для исследования приведенных выше уравнений нам пришлось бы учитывать бесконечное их число, действующих на каждую частицу тела. Но решение этой задачи можно упростить, если вместо реальных сил тяжести ввести расчетный вектор, равный сумме сил тяжести отдельных его частей, приложенный к центру масс. При этом мы заменим бесконечное число сил одной расчетной силой тяжести и получим, как говорят, эквивалентную систему сил. Суть такой замены состоит в том, что она позволяет упростить расчеты, не изменяя решений уравнений и .
Таким образом, основной задачей статики является установление законов преобразования системы сил в эквивалентные системы с целью упрощения расчетов для решений уравнений равновесия.
Методы статики применяются не только для изучения неподвижных тел, но и для движущихся. Это связано с тем, что если заменить исходную систему сил на эквивалентную, то законы движения тела, или как говорят, кинематическое состояние тела, от этого не изменится. Поэтому методы статики применяются к любым механическим системам, состоящих из точек и твердых тел независимо от того, покоятся они или совершают движение. Эти методы позволяют привести исходную систему сил к эквивалентной с целью упрощения расчетов. Таким образом силы в статике и в теоретической механике являются чисто расчетными величинами. Они могут отличаться от реальных сил, действующих на тела, которые применяются в физике или теории упругости. Все эти методы применяются только к абсолютно твердым телам, пренебрегая возможными деформациями внутри самих тел.
Статика и эквивалентные преобразования сил
Снова рассмотрим уравнения движения твердого тела:(2) ;(3) . Пусть в момент времени нам известны внешние силы , действующие на тело. Далее мы можем попытаться упростить систему сил, сведя ее эквивалентными преобразованиями к новой системе . В следующий момент времени, силы могут измениться и нам потребуется выполнять новые эквивалентные преобразования. В этом, конечно, ничего хорошего нет. Но, возможно, нам удастся найти эквивалентные преобразования аналитическим способом, то есть получить аналитическое выражение для новых сил , пригодное для любого момента времени. Тогда вместо и мы получим систему уравнений с более простой системой сил:(2′) ;(3′) .
Теперь из уравнений и вычтем уравнения и :(4) ;(5) . Но это есть ни что иное, как уравнения статики, в которых к исходной системе сил добавили эквивалентную систему, изменив направления на противоположные.
Отсюда следует вывод, что для получения эквивалентной системы сил, нужно к исходной системе, добавить новую систему сил так, чтобы тело находилось в равновесии. Тогда эквивалентная система будет совпадать с новой, в которой направления сил заменены на противоположные.
Силы в теоретической механике
Если мы рассматриваем деформации в телах, то все приложенные силы нужно рассматривать как связанные векторы, поскольку внутренние напряжения и деформации зависят от точек приложения сил. Но если мы считаем тело абсолютно твердым, и нам нужно определить только траекторию его движения, то, как показано выше, силы являются скользящими векторами. То есть в теоретической механике мы можем обращаться с силами более свободно, чем при решении других задач – точки приложения сил можно перемещать вдоль линий их действия.
Таким образом, в теоретической механике, над силами мы можем выполнять следующие преобразования.1) Переносить точку приложения силы на любое расстояние вдоль линии ее действия.2) Раскладывать силу по правилу параллелограмма на две или более сил, каждая из которых приложена в той точке, что исходная сила – то есть можно заменить исходную силу на несколько сил, векторная сумма которых равна исходной.3) Несколько сил, приложенных к одной точке можно объединять в одну, применяя правило параллелограмма – то есть можно заменить несколько сил, приложенных в одной точке их векторной суммой, приложенной в той же точке.
Такие преобразования называются эквивалентными преобразованиями сил. А системы, полученные в результате таких преобразований, называются эквивалентными системами сил. На странице «Аксиомы статики» приводится иллюстрация подобных преобразований. См. Таким образом, в теоретической механике, силы являются некоторыми расчетными величинами. Их можно преобразовывать для того, чтобы получить более простую систему сил и упростить уравнения движения тел.
Рассмотрим следующий пример. Пусть мы имеем тело, на которое действует сила тяжести Земли. Эта сила приложена ко всем точкам. На любую малую часть тела, массой , действует сила тяжести , где – ускорение свободного падения. То есть на тело действует система сил, равномерно распределенных по его объему. Решать уравнения движения с такими силами неудобно. Поэтому в начале, проще выполнить эквивалентные преобразования. В результате таких преобразований все силы тяжести малых элементов тела можно заменить одной силой , приложенной к центру масс тела с радиус-вектором . Тем самым мы пришли к уравнениям движения, в которых на тело действует одна сила. Естественно, что это не реальная сила, действующая в центре масс, а расчетная величина, эквивалентная распределенным по объему тела силам.
Здесь мы разбили тело на материальные точки, каждая из которых имеет массу и положение в пространстве, задаваемое радиус-вектором . Тогда – масса тела. Суммирование выполняется по всем точкам, составляющим тело.
Примеры решения задач
Решение примеров по теме: «Статика твердого тела»
Пример 1. Условия равновесия
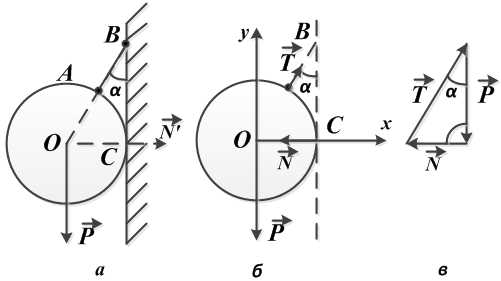
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.
Дано: P = 10 Н; α = 45°Найти: N, T — ?
Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.
Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).
Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).
При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).
В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:
После подстановки в формулы числовых значений, получим: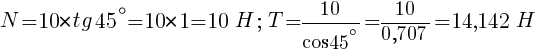 .
.
Ответ: .
Решение примеров по теме: «Кинематика»
Пример 2. Уравнение траектории точки
Дано:
Движение точки задано уравнениями ;
(x, у — в сантиметрах, t — в секундах).Найти: уравнение траектории точки в координатной форме.
Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла: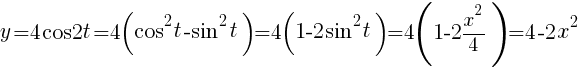 .
.
Опуская промежуточные выражения, получаем уравнение траектории:.
Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).
Ответ: .
Решение примеров по теме: «Динамика»
Пример 3. Основной закон динамики точки
Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.
Дано: m = 10 кг; a = 0,5 м/с2.Найти: F — ?
Решение.
Согласно основному закону динамики: .
Подставив значения в формулу, получим:
Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с2, равна 5 Н.
В помощь студенту
- Формулы, правила, законы, теоремы, уравнения, примеры решения задач
- Теоретические основы электротехники
- Электрические машины
- Высшая математика
Скользящие векторы
Теперь рассмотрим абсолютно твердое тело. Законы его движения имеют более сложный вид. Они описываются двумя векторными уравнениями:(2) ;(3) . Здесь – ускорение центра масс тела; – его масса; – момент импульса тела относительно произвольно выбранного центра ; – внешние силы, действующие на тело, приложенные в точках .
Вместо того, чтобы пытаться в лоб решать эти уравнения, давайте попробуем вывести некоторые закономерности, заключенные в этих уравнениях. Для этого упростим задачу. Рассмотрим тело в некоторый момент времени . И пусть, для этого момента времени, нам известны действующие на него силы и точки их приложения .
Уравнение не зависит от точек приложения сил. Для его составления требуется знать только проекции сил на оси координат . А вот в уравнение входят точки приложения. Они входят в виде векторов, проведенных из некоторого центра в точку . Причем входят в виде векторного произведения .
Согласно одному из свойств, векторное произведение векторов, имеющих одинаковое направление, равно нулю. Поэтому . Тогда если к вектору прибавить любой вектор, параллельный , то векторное произведение не изменится:. Здесь – произвольная постоянная, имеющая размерность м/Н.
Отсюда следует важный вывод. Если точку приложения силы переместить на любое расстояние вдоль линии действия силы, то уравнения движения твердого тела не изменятся. В связи с этим, вместо обычного в математическом определении вектора, можно ввести новый математический объект, называемый скользящим вектором. Скользящий вектор по существу есть множество, состоящее из двух векторов – самого вектора силы (так называемый образующий вектор) и его точки приложения относительно выбранного центра системы отсчета . В связи с этим, приводим следующие определения.
- Скользящий вектор
- – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, проведенной через точку приложения параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
Наряду со скользящим вектором, мы можем ввести понятия закрепленных и свободных векторов.
- Закрепленный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два фиксированных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
- Свободный вектор
- – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Таким образом, свободный вектор не зависит от точки приложения, и является просто вектором. Для справок также приведем определение вектора.
- Вектор в трехмерном пространстве
- – это три числа, называемые компонентами, связанные с предварительно выбранной прямоугольной системой координат, которые при поворотах этой системы вокруг ее центра , и при отражении осей, преобразуются по тому же закону, что и координаты произвольной точки , не совпадающей с . Компоненты вектора также называются проекциями вектора на оси координат.
Условия равновесия системы сходящихся сил
Теорема 1
Для равновесия системы сходящихся сил (далее система сил) необходимо и достаточно, чтобы равнодействующая сила была равна нулю: $R=0$
Необходимость условия равновесия следует из того, что заданная система сил, приложенных к твердому телу, эквивалентна одной силе — равнодействующей $Р$. Очевидно, что под действием одной силы тело будет находиться в равновесии только тогда, когда эта сила равна нулю, что следует из аксиомы о двух силы.
Докажем достаточность этого условия. Для этого покажем, что когда равнодействующая сила равна нулю, то система сил находится в равновесии. Заданная система сил эквивалентна равнодействующей, равной нулю. Из определения уравновешенной (эквивалентной нулю) системы сил, ее можно отбросить, не нарушая состояния системы. Тогда на тело не действуют никакие силы, и оно по первому закону Ньютона находится в равновесии. Поскольку
$ \vec{R} = \sum \limits_{i=i}^{n} = \vec{F_i} = 0$
то многоугольник сил должен быть замкнутым, то есть конец последней силы $F$ совпадает с началом первой силы, $F_1$, что выражает условие равновесия системы сил в графической форме.
Векторной части равенства соответствуют три скалярные части равенства:
$R_x=0$,
$R_y=0$,
$R_z=0$, которые с учетом формул, перепишем в виде
$ \sum \limits_{i=i}^{n} = F_ix = 0$
$ \sum \limits_{i=i}^{n} = F_iy = 0$
$ \sum \limits_{i=i}^{n} = F_iz = 0$
Эти данные являются условиями равновесия системы сил в аналитической форме и формулируются так: для равновесия пространственной системы сил необходимо и достаточно, чтобы алгебраические суммы проекций сил были взаимно перпендикулярные оси и равны нулю.
В случае равновесия системы сил, лежащих в одной плоскости, например, $0xy$, получим
$ \sum \limits_{i=i}^{n} = F_ix = 0$
$ \sum \limits_{i=i}^{n} = F_iy = 0$
Условия равновесия называются также уравнениями равновесия. С их помощью определяются неизвестные величины при решении конкретных задач. Если неизвестными силами являются реакции связей, то их количество не должно превышать числа уравнений равновесия, иначе задача будет статически неопределенной и решить ее методами теоретической механики не получится.