Теорема о среднем ролля, лагранжа и коши для дифференцируемых функций.

Формула конечных приращений Лагранжа.

Теорема Лагранжа.

Если функция $f(x)$ непрерывна на отрезке  и дифференцируема на интервале $(a,b)$, то в этом интервале найдется хотя бы одна точка $\xi$ такая, что
$$
f(b)-f(a)=f'(\xi)(b-a).\label{ref11}
$$

$\circ$ Рассмотрим функцию
$$
\varphi(x)=f(x)+\lambda x,\nonumber
$$
где число $\lambda$ выберем таким, чтобы выполнялось условие $\varphi(a)=\varphi(b)$, то есть $f(a)+\lambda a=f(b)+\lambda b$. Отсюда находим
$$
\lambda=-\frac{f(b)-f(a)}{b-a}.\label{ref12}
$$
Так как функция $\varphi(x)$ непрерывна на отрезке , дифференцируема на интервале $(a,b)$ и принимает равные значения в концах этого интервала, то по существует точка $\xi\in(a,b)$ такая, что $\varphi'(\xi)=f'(\xi)+\lambda=0$. Отсюда в силу условия \eqref{ref12} получаем равенство
$$
f'(\xi)=\frac{f(b)-f(a)}{b-a},\label{ref13}
$$
равносильное равенству \eqref{ref11}. $\bullet$

Рис. 17.7

Замечание 4.

Правая часть, формулы \eqref{ref13} равна угловому коэффициенту секущей, которая проходит через точки $A(a,f(a))$ и $B(b,f(b))$ графика функции $y=f(x)$, а левая часть этой формулы равна угловому коэффициенту касательной к графику в точке $(\xi,f(\xi))$. Поэтому теорема Лагранжа имеет следующую геометрическую интерпретацию: существует значение $\xi\in(a,b)$ такое, что касательная к графику функции $y=f(x)$ в точке $(\xi,f(\xi))$ параллельна секущей (рис. 17.7), соединяющей точки $A(a,f(a))$ и $B(b,f(b))$.

Рис. 17.8

Замечание 5.

Пусть функция $f$ удовлетворяет условиям . Если $x_{0}\in$, а приращение $\Delta x\neq 0$ таково, что точка $x_{0}+\Delta x$ также принадлежит отрезку , то, применив теорему Лагранжа к функции $f(x)$ на отрезке $l$ с концами $x_0$ и $x_0+\Delta x$ ($\Delta x$ может быть и отрицательным), получим
$$
f(x_{0}+\Delta x)-f(x_{0})=\Delta xf'(\xi),\label{ref14}
$$
где $\xi$ — некоторая внутренняя точка отрезка $l$.

Пусть, $\Delta x > 0$; тогда $0 < \xi-x_0 < \Delta x$ (), и поэтому $0 < \displaystyle \frac{\xi-x_{0}}{\Delta x} < 1$. Полагая $\theta=\displaystyle \frac{\xi-x_{0}}{\Delta x}$, получаем
$$
\xi=x_0+\theta\Delta х,\ где \ 0 < \theta < 1.\label{ref15}
$$
Аналогично, если $\Delta x < 0$, то $0 < x_0-\xi < |\Delta x|$, и поэтому $0 < \displaystyle \frac{x_{0}-\xi}{-\Delta x} < 1$. Полагая $\displaystyle \theta=\frac{x_{0}-\xi}{-\Delta x}=\frac{\xi-x_{0}}{\Delta x}$, снова получаем равенство \eqref{ref15}, где $0 < \theta < 1$.

Следовательно, равенство \eqref{ref14} можно записать в виде
$$
f(x_0+\Delta x)-f(x_0)=\Delta xf'(x_0+\theta \Delta x),\label{ref16}
$$
где $0 < \theta < 1$.
Формулу \eqref{ref16} называют формулой конечных приращений Лагранжа. Она дает точное выражение для приращения функции, в отличие от приближенного равенства
$$
f(x_0+\Delta x)-f(x_0)\approx\Delta xf'(x_{0}),\nonumber
$$
которое иногда называют формулой бесконечно малых приращений.

Пример 1.

Доказать, что

$$
\operatorname{ln}(1+x) < x\ при\ x > 0,\label{ref17}
$$
$$
|\operatorname{arctg}x_2-\operatorname{arctg}x_1|\leq|x_{2}-x_{1}|,\quad x\in\mathbb{R},\ x\in\mathbb{R}.\label{ref18}
$$

$\triangle$ Применяя теорему Лагранжа к функции $f(x)=\operatorname{ln}(1+x)$ на отрезке , где $x > 0$, получаем $\operatorname{ln}(1+x)=\displaystyle \frac{1}{1+\xi}x$ откуда следует неравенство \eqref{ref17}, так как $0 < \xi < x$.
По теореме Лагранжа для функции $\operatorname{arctg}x$ на отрезке с концами $x_1$ и $x_2$ находим
$$
\operatorname{arctg}x_2-\operatorname{arctg}x_1=\frac{1}{1+\xi^{2}}(x_2-x_1),\nonumber
$$
откуда получаем $|\operatorname{arctg}x_2-\operatorname{arctg}x_{2}|=\displaystyle \frac{|x_{2}-x_{1}|}{1+\xi^{2}}\leq|x_{2}-x_{1}|$, так как $0 < \displaystyle \frac{1}{1+\xi^{2}}\leq 1$. $\blacktriangle$

Полагая в соотношении \eqref{ref18} $x_2=x,\ x_1=0$, получаем
$$
|\operatorname{arctg}x|\leq|x|,\quad x\in\mathbb{R},\label{ref19}
$$
и, в частности,
$$
0\leq\operatorname{arctg}x\leq x,\quad x\geq 0.\label{ref20}
$$

Теорема Коши.[]

Если функции f(x){\displaystyle f(x)} и g(x){\displaystyle g(x)} непрерывны на отрезке a,b{\displaystyle }, дифференцируемы на интервале (a,b){\displaystyle (a,b)}, причем g′(x)≠{\displaystyle g'(x)\neq 0} во всех точках этого интервала, то найдется хотя бы одна точка ξ∈(a,b){\displaystyle \xi \in (a,b)} такая, что

f(b)−f(a)g(b)−g(a)=f′(ξ)g′(ξ){\displaystyle {\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(\xi )}{g'(\xi )}}}.

Доказательство.

Рассмотрим функцию

φ(x)=f(x)+λg(x),{\displaystyle \varphi (x)=f(x)+\lambda g(x),}

где число λ{\displaystyle \lambda } выберем таким, чтобы выполнялось равенство φ(a)=φ(b){\displaystyle \varphi (a)=\varphi (b)}, которое равносильно следующему:

f(b)−f(a)+λ(g(b)−g(a))= (1){\displaystyle f(b)-f(a)+\lambda (g(b)-g(a))=0.~~~~(1)}

Заметим, что g(b)≠g(a){\displaystyle g(b)\neq g(a)}, так как в противном случае согласно теореме Ролля существовала бы точка c∈(a,b){\displaystyle c\in (a,b)} такая что g′(c)={\displaystyle g'(c)=0} вопреки условиям теоремы.

Итак, g(b)−g(a)≠{\displaystyle g(b)-g(a)\neq 0} и из равенства (1) следует, что

λ=−f(b)−f(a)g(b)−g(a). (2){\displaystyle \lambda =-{\frac {f(b)-f(a)}{g(b)-g(a)}}.~~~~~(2)}

Так как функция φ{\displaystyle \varphi } при любом λ{\displaystyle \lambda } непрерывна на отрезке a,b{\displaystyle } и дифференцируема на интервале (a,b){\displaystyle (a,b)}, а при значение λ{\displaystyle \lambda } определяемом формулой (2), принимает равные значения в точках a{\displaystyle a} и b{\displaystyle b}, то по теореме Ролля существует точка ξ∈(a,b){\displaystyle \xi \in (a,b)} такая, что φ′(ξ)={\displaystyle \varphi ‘(\xi )=0}, откуда f′(ξ)g′(ξ)=−λ{\displaystyle {\frac {f'(\xi )}{g'(\xi )}}=-\lambda }. Из этого равенства следует утверждение теоремы.

Теорема Ролля

Теорема 1

Пусть функция $f(x)$ непрерывна на $$, дифференцируема в (а, b) и на концах отрезка принимает значения $f(a) = f(b)$. Тогда существует точка с принадлежащая $(а, b)$ и $f'(c) =0$.

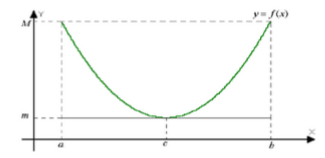Рисунок 1. Функция f(x)

Таким образом, теорема утверждает, что на графике существует такая точка, в которой касательная параллельна оси ОХ.

Доказательство

Поскольку функция непрерывна на отрезке $$ она имеет наименьшее значение m и наибольшее значение М на данном промежутке.

Рассмотрим два возможных исхода. Пусть m = M. Тогда очевидно, что функция f(x)=const и ее производная равна 0 на всех точках заданного промежутка.

Если минимальное и максимальное значение не совпадают, т.е. $m ≠ M$ то функция принимает наименьшее или наибольшее значение только внутри интервала (а, b). Пусть в точке с принадлежащей отрезку $(а, b), f(c) = m$, тогда левая и правая производные имеют в данной точке конечную производную и равны между собой значению $f ‘(с)$.

Следовательно,

По свойству пределов следует, что $f'(c)\ge 0$. Рассуждая аналогично, можно сделать вывод, что $f'(c)\le 0$. Но поскольку $f’_{-} (c)=f’_{+} (c)=f’_{} (c)$ то $f’_{} (c)=0$.

Пример 1

Показать, что функция

Удовлетворяет условиям теоремы Ролля на промежутке и найти точку с принадлежащую данному отрезку, если $f'(c) = 0$.

Решение.

Функция дифференцируема на промежутке и как слева, так и справа равна 0

$f(1) = f(2) = 0$

Найдем точку, в которой производная равна 0.

Из полученной производной выразим х

$2х — 3 = 0$

$х = 1,5$

Т.е. точка, с в которой производная равна 0, равна 1,5