Что такое противоположное событие?

Условная вероятность

Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.

С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.

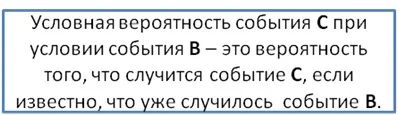
Обозначается она так:

Р(С|B).

Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.

Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения

Р(А) = Р(В)•Р(С|B)

Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?

Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:

Р = (1/13)•(1/17) = 1/221 ≈ 0,004525

Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:

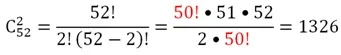
Но всего 6 способами можно выбрать 2 шара из 4:

Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:

Р = 6/1326 = 1/221.

Ответ: 1/221

Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?

Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать

Р(А) = Р(В)•Р(С|B)

По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):

Р(А) = Р(В)•Р(С|B)

0,01326 = 0,05126•Р(С|B)

Р(С|B) = 0,01326/0,05126 ≈ 0,2587

Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.

Ответ: 0,2587

Значение противоположных событий в жизни

Каждый день мы сталкиваемся с разными событиями, и важно понимать, что за каждым событием может следовать противоположное. Это отражает закономерность жизни — все вокруг нас состоит из противоположностей: свет-тень, радость-горе, успех-поражение

Противоположные события не только разнообразят нашу жизнь, но и помогают нам лучше понимать самих себя. Без трудностей и рисков мы не может развиваться и не успеваем оценить свои достижения. К примеру, успехи считаются ценными только на фоне неудач и неудачи являются уроками нашей жизни, которые помогают растить и развиваться.

Противоположные события также помогают нам оценить ценность и важность вещей и людей в нашей жизни. Например, мы ощущаем настоящую радость, только если нам известно печальное чувство горя

Или же мы оцениваем доброту и заботу близких людей особенно когда нам сложно и трудно.

Кроме того, понимание противоположных событий помогает нам лучше управлять своей жизнью. Если мы знаем, что где есть свет, там обязательно будут и тени, то мы не будем переживать, когда за светом последуют тени. Напротив, мы сможем оценить и ценить каждый миг своей жизни, будь то светлий или темный.

Вывод 1: Противоположные события являются неотъемлемой частью жизни.
Вывод 2: Противоположные события помогают нам оценить ценность и важность вещей и людей в нашей жизни.
Вывод 3: Понимание противоположных событий помогает нам лучше управлять своей жизнью.

Геометрическая вероятность

В классическом определении вероятности рассматривается
полная группа конечного числа равновозможных событий. На практике
очень часто число возможных исходов испытаний бесконечно. В таких
случаях классическое определение вероятности неприменимо. Однако
иногда в подобных случаях можно воспользоваться другим методом
вычисления вероятности. Для определенности ограничимся двумерным
случаем.

Пусть на плоскости задана некоторая областьплощадью, в
которой содержится другая областьплощадью(рис.
3). В областьнаудачу
бросается точка. Чему равна вероятность того, что точка попадет в
область? При
этом предполагается, что наудачу брошенная точка может попасть в
любую точку области, и
вероятность попасть в какую-либо часть областипропорциональна
площади части и не зависит от ее расположения и формы. В таком
случае вероятность попадания в областьпри
бросании наудачу точки в область

(1.3)

Таким образом, в общем случае, если возможность
случайного появления точки внутри некоторой области на прямой,
плоскости или в пространстве определяется не положением этой области
и ее границами, а только ее размером, т. е. длиной, площадью или
объемом, товероятность
попадания случайной точки внутрь некоторой области определяется как
отношение размера этой области к размеру всей области, в которой
может появляться данная точка. Это есть геометрическое определение
вероятности.

Пример 3.Круглая
мишень вращается с постоянной угловой скоростью. Пятая часть мишени
окрашена в зеленый цвет, а остальная — в белый (рис. 4). По мишени
производится выстрел так, что попадание в мишень — событие
достоверное. Требуется определить вероятность попадания в сектор
мишени, окрашенный в зелёный цвет.

Решение.Обозначим—
«выстрел попал в сектор, окрашенный в зелёный цвет». Тогда.
Вероятность получена как отношение площади части мишени, окрашенной
в зелёный цвет, ко всей площади мишени, поскольку попадания в любые
части мишени равновозможны.

Фактчек

• Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 
• События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 
• События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A \(\cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A \cup B) = P(A) + P(B) — P(A \cap B).
• События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A). 
• Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Частота и вероятность

В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.

Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.

Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.

Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:

• Бросок кубика с 6 гранями – это эксперимент, а выпадение или невыпадение шестерки на нем – это случайное событие.
• Полет самолета – испытание, а отказ двигателя в полете – это случайное событие.
• Ожидание автобуса на остановке в течение 10 минут – эксперимент, а появление или непоявление автобуса в этот промежуток времени – случайное событие.
• Футбольный матч – опыт, а победа в нем команды хозяев или травма одного из игроков – случайное событие.
• Выстрел из винтовки – испытание, а попадание в мишень – случайное событие.
• Изготовление рабочим детали – эксперимент, а получение бракованной детали – случайное событие.

Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет

Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.

Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна

85/500 = 0,17

Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.

Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.

Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).

Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в . Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.

2.4. Принцип практической невозможности маловероятных событий

При решении многих практических задач приходится иметь дело
с событиями, вероятность которых весьма мала, т.е. близка к нулю. Можно ли
считать, что маловероятное событие  в
единичном испытании не произойдет? Такого заключения сделать нельзя, так как не
исключено, хотя и мало вероятно, что событие  наступит.

Казалось бы, появление или непоявление маловероятного
события в единичном испытании предсказать невозможно. Однако длительный опыт
показывает, что маловероятное событие в единичном испытании в подавляющем
большинстве случаев не наступает. На основании этого факта принимают следующий
«принцип практической невозможности маловероятных событий»: если случайное
событие имеет очень малую вероятность, то практически можно считать, что в
единичном испытании это событие не наступит.

Естественно возникает вопрос: насколько малой должна быть
вероятность события, чтобы можно было считать невозможным его появление в одном
испытании? На этот вопрос нельзя ответить однозначно. Для задач, различных по
существу, ответы разные. Например, если вероятность того, что парашют при прыжке
не раскроется, равна 0,01, то было бы недопустимым применять такие парашюты.
Если же вероятность того, что поезд дальнего следования прибудет с опозданием,
равна 0,01, то можно практически быть уверенным, что поезд прибудет вовремя.

Достаточно малую вероятность, при которой (в данной
определенной задаче) событие можно считать практически невозможным, называют
уровнем значимости.

На практике обычно принимают уровни значимости, заключенные
между 0,01 и 0,05. Уровень значимости, равный 0,01, называют однопроцентным;
уровень значимости, равный 0,02, называют двухпроцентным, и т.д.

Подчеркнем, что рассмотренный здесь принцип позволяет делать предсказания не
только о событиях, имеющих малую вероятность, но и о событиях, вероятность
которых близка к единице. Действительно, если событие  имеет
вероятность, близкую к нулю, то вероятность противоположного события  близка
к единице. С другой стороны, непоявление события  означает
наступление противоположного события

Таким образом, из принципа невозможности маловероятных событий вытекает
следующее важное для приложений следствие: если случайное событие имеет
вероятность, очень близкую к единице, то практически можно считать, что в
единичном испытании это событие наступит. Разумеется, и здесь ответ на
вопрос о том, какую вероятность считать близкой к единице, зависит от существа
задачи

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Проверь себя

Задание 1. Какие события являются несовместными?

1. Подбрасывание монетки.
2. Брак батареек в одной упаковке.
3. “Миша идет” и “Миша стоит”.
4. Случайное вытаскивание конфет из вазы. 

Задание 2. Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

1. 0,17
2. 1
3. 0,83
4. 1,17 

Задание 3. Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1. 1
2. 0,216
3. 0,45
4. 1,5 

Задание 4. В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут. 

1. 0,3
2. 0,001
3. 2,7
4. 0,729 

Задание 5. Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой. 

1. 0,77
2. 0,135
3. 0,23
4. -0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

Задачи

Пример 1

В классе 27 учеников. Из них:

17 изучали немецкий язык,

6 — английский,

2 — оба языка.

Найти вероятность того, что случайно выбранный ученик изучал хотя бы один язык.

Что мы знаем:

𝑃(N) = 17/27,

𝑃(A) = 6/27,

𝑃(N ∙ A) = 2/27.

Значит вместе это будет:

𝑃(N + A) = 𝑃(N) + 𝑃(A) − 𝑃(N ∙ A) = 17/27 + 6/27 − 2/27 = 21/27 = 7/9.

Пример 2

Лотерейные билеты пронумерованы от 1 до 100. Какова вероятность того, что в выбранном билете будет стоять число больше 40 или чётное число?

Что мы знаем:

P(>40) = 60/100 = 6/10 = 3/5

P(Ch) = ½ = 5/10

Логическое ИЛИ означает, что нам нужно произвести операцию сложения (т. е. сумма событий).

Нам понадобится формула сложения совместных событий P(A + B) = P(A) + P(B) — P(AB).

Для этого нам нужно узнать сколько будет P(>40 . Ch), для этого используем формулу P(AB) = P(A) . P(B).

P(>40 . Ch) = P(>40) . P(Ch) = ⅗ . ½ = 3/10

Теперь можем подставить всё в формулу P(A + B) = P(A) + P(B) — P(AB):

P(>40 + Ch) = P(>40) + P(Ch) — P(>40.Ch) = 6/10 + 5/10 — 3/10 = 8/10 = ⅘.

Пример 3

В финале международного турнира по стрельбе из лука участвовали 8 спортсменов: 3 американца, 1 англичанин, 1 немец, 1 француз и 2 русских. Какова вероятность того, что хотя бы один русский попадёт в тройку лучших, учитывая, что все спортсмены имеют равные условия для получения медали (золотой, серебряной и бронзовой).

Что мы знаем:

Когда в вопросе появляется «хотя бы один», можно «пойти от противного» — мы должны найти вероятность того, что этого не произойдёт (на пьедестале русских не будет), а затем вычесть это из 1.

P (никакой русский не выиграет золото) = 6/8 = 3/4

P (никакой русский не выиграет серебро) = 5/7 (убираем золотую медаль)

P (никакой русский не выиграет бронзу) = 4/6 = 2/3 (убираем золотую и серебряную медали)

P (на пьедестале не будет русских) = 3/4 x 5/7 x 2/3 = 30/84 = 5/14

P (хотя бы один русский на пьедестале) = 1 – 5/14 = 14/14 – 5/14 = 9/14.

Примеры противоположных событий

Противоположные события — это события, которые исключают друг друга и не могут произойти одновременно. Например:

• Бросок монеты выпадает орел или решка.
• Монета не может выпасть одновременно орлом и решкой.
• Бросок кубика выпадает число или не число.
• Выпадение одного числа исключает выпадение другого.
• Студенты получают либо зачет, либо не получают.
• Получение зачета исключает не получение его.

Если одно событие является противоположным другому, то вероятность каждого из событий равна 0.5. Для вычисления вероятности противоположного события необходимо вычесть вероятность данного события из единицы.

Таблица вероятностей
Событие
Вероятность
Противоположное событие
Вероятность

Орел
0.5
Решка
0.5

Решка
0.5
Орел
0.5

Число
0.5
Не число
0.5

Не число
0.5
Число
0.5

Зачет
0.5
Не зачет
0.5

Не зачет
0.5
Зачет
0.5

Использование противоположных событий может быть полезно для вычисления вероятности сложных событий. Например, вероятность выпадения орла или решки при броске монеты равна 1, так как это противоположное событие от выпадения монеты на ребро.

Элементарные события

Часто одно случайное событие можно представить как результат нескольких случайных событий. Например, событие «выпадение на кубике четного числа» произойдет в том случае, если случится хотя бы одно из следующих событий:

• выпадет двойка;
• выпадет четверка;
• выпадет шестерка.

Если событие нельзя «разбить» на более простые события, то его называют элементарным событием. Считается, что в ходе испытания может произойти только одно элементарное событие. Так, при броске кубика произойдет одно из 6 элементарных событий:

• выпадет единица;
• выпадет двойка;
• выпадет тройка;
• выпадет четверка;
• выпадет пятерка;
• выпадет шестерка.

В большинстве случаев вероятность элементарных событий одинакова. Действительно, нет причин полагать, что при броске кубика шестерка будет выпадать чаще двойки. Если у двух элементарных событий одинаковая вероятность, то их называют равновозможными событиями.

Если в результате эксперимента происходит одно из равновозможных событий, число которых равно n, то вероятность каждого из них принимается равной дроби 1/n.

Например, при броске кубика может произойти 6 равновозможных событий. Значит, вероятность каждого из них равна 1/6. При броске монетки она может выпасть либо орел, либо решка. Этих событий два, и они равновозможны, поэтому их вероятность равна 1/2, то есть 0,5.

Пример. В урне 20 шариков, один из которых окрашен в желтый цвет. Какова вероятность, что человек, вытаскивающий вслепую один из шариков, вынет именно желтый шар?

Решение. Так как шаров 20, то возможны 20 равновозможных событий, одно из которых – вытаскивание желтого шара. Его вероятность равна 1/20 = 0,05

Ответ: 0,05

Пример. Вася составил произвольную последовательность из букв А, Б, В, Г, Д, и записал ее на бумаге. Каждую букву Вася использовал один раз. Аналогично свою последовательность записал и Петя. Какова вероятность, что они оба загадали одну и ту же последовательность.

Решение. Вася записал перестановку 5 букв. Общее количество таких перестановок равно 5! = 1•2•3•4•5 = 120. Все последовательности равновероятны. Значит, вероятность того, что они совпали, равна 1/120.

Ответ: 1/120

Алгебра событий

Операция сложения событий означает логическую связку ИЛИ, а операция умножения событий — логическую связку И.

Сложение событий

Суммой двух событий A и B называется событие A+B, которое состоит в том, что наступит или событие A, или событие B, или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие A, или событие B.

Правило распространяется и на большее количество слагаемых, например, событие A₁ + A₂ + A₃ + A₄ + A₅ состоит в том, что произойдет хотя бы одно из событий A₁, A₂, A₃, A₄, A₅, а если события несовместны — то одно и только одно событие из этой суммы: или событие A₁, или событие A₂, или событие A₃, или событие A₄, или событие A₅.

Примеров масса:

• Событие (при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

Событие B_{1, 2} = B₁ + B₂ (выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

Событие B_Ч = B₂ + B₄ + B₆ (будет чётное число очков) состоит в том, что выпадет или 2 , или 4 , или 6 очков.

Умножение событий

Произведением двух событий A И B называют событие AB, которое состоит в совместном появлении этих событий. Иными словами, умножение AB означает, что при некоторых обстоятельствах наступит и событие A, и событие B. Аналогичное утверждение справедливо и для большего количества событий: например, произведение A₁A₂A₃ … A₁₀ подразумевает, что при определенных условиях произойдет и событие A₁, и событие A₂, и событие A₃,…, и событие A₁₀.

Рассмотрим испытание, в котором подбрасываются две монеты, и следующие события:

• A₁ — на 1-й монете выпадет орел;

Ā₁ — на 1-й монете выпадет решка;

A₂ — на 2-й монете выпадет орел;

Ā₂ — на 2-й монете выпадет решка.

Тогда:

• событие A₁A₁ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орел;

событие Ā₂Ā₂ состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;

событие A₁Ā₂ состоит в том, что на 1-й монете выпадет орел и на 2-й монете решка;

событие Ā₁A₂ состоит в том, что на 1-й монете выпадет решка и на 2-й монете орел.

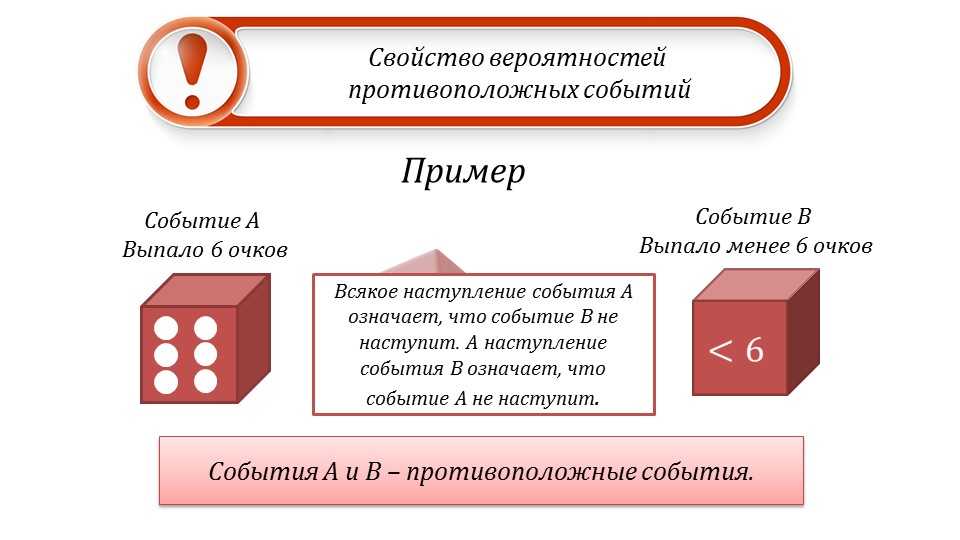
Противоположные события

Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.

Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:

0,7 + 0,3 = 1

Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.

Противоположными являются такие события, как:

• падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
• выпадение четного или нечетного числа на шестигранном кубике;
• изготовление рабочим годной или получение бракованной детали.

Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.

Очевидно, что сумма вероятностей противоположных событий равна единице.

Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?

Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице

Р(А) + Р(B) = 1

По условию Р(А) = 0,97. Тогда

0,97 + Р(В) = 1

Перенесем в равенстве слагаемое 0,97 в правую часть и получим:

Р(B) = 1 – 0,97

Р(В) = 0,03

Ответ: 0,03

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться. 

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов. 

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат. 

Как кот может быть одновременно жив и мертв? Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом. По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив. Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным.  Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

• выпадет орел;
• выпадет решка. 

Эти два события образуют множество элементарных событий. 

Множество элементарных событий — множество всех возможных результатов случайного эксперимента. 

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации. 

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран. 

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности. 

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу. 

\(P = \frac{m}{n}\)

Вероятность можно обозначить, как P(x), где х — некоторое событие. 

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Можно ли всегда выигрывать спор с монеткой?Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна \(P = \frac{2}{2} = 1\), то есть мы точно выиграем спор. Однако вероятность не так проста, и даже здесь подготовила ловушку. В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет  \(\frac{1}{6000}\). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%. 

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна \(\frac{49}{140} = 0,35\)

Выразим в процентах:  0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ. 

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой. 

\(P = \frac{m}{n} * 100%\)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.

Классификация событий

Одним из основных понятий теории вероятностей является понятие события.
Подсобытиемпонимают
любой факт, который может произойти в результате опыта или
испытания. Подопытом,
илииспытанием,
понимается осуществление определённого комплекса условий.

Примеры событий:

– попадание в цель при выстреле из орудия (опыт —
произведение выстрела; событие — попадание в цель);
– выпадение двух гербов при трёхкратном бросании монеты (опыт —
трёхкратное бросание монеты; событие — выпадение двух гербов);
– появление ошибки измерения в заданных пределах при измерении
дальности до цели (опыт — измерение дальности; событие — ошибка
измерения).

Можно привести бесчисленное множество подобных примеров.
События обозначаются заглавными буквами латинского алфавитаи
т.д.

Различаютсобытия
совместныеинесовместные.
События называются совместными, если наступление одного из них не
исключает наступления другого. В противном случае события называются
несовместными. Например, подбрасываются две игральные кости. Событие—
выпадание трех очков на первой игральной кости, событие—
выпадание трех очков на второй кости.и—
совместные события. Пусть в магазин поступила партия обуви одного
фасона и размера, но разного цвета. Событие—
наудачу взятая коробка окажется с обувью черного цвета, событие—
коробка окажется с обувью коричневого цвета,и—
несовместные события.

Событие называетсядостоверным,
если оно обязательно произойдет в условиях данного опыта.

Событие называется невозможным, если оно не может произойти в условиях
данного опыта. Например, событие, заключающееся в том, что из партии
стандартных деталей будет взята стандартная деталь, является
достоверным, а нестандартная — невозможным.

Событие называетсявозможным,
илислучайным,
если в результате опыта оно может появиться, но может и не
появиться. Примером случайного события может служить выявление
дефектов изделия при контроле партии готовой продукции,
несоответствие размера обрабатываемого изделия заданному, отказ
одного из звеньев автоматизированной системы управления.

События называютсяравновозможными,
если по условиям испытания ни одно из этих событий не является
объективно более возможным, чем другие. Например, пусть магазину
поставляют электролампочки (причем в равных количествах) несколько
заводов-изготовителей. События, состоящие в покупке лампочки любого
из этих заводов, равновозможны.

Важным понятием являетсяполная
группа событий. Несколько событий в данном опыте образуют
полную группу, если в результате опыта обязательно появится хотя бы
одно из них. Например, в урне находится десять шаров, из них шесть
шаров красных, четыре белых, причем пять шаров имеют номера.—
появление красного шара при одном извлечении,—
появление белого шара,—
появление шара с номером. Событияобразуют
полную группу совместных событий.

Введем понятие противоположного, или дополнительного, события. Подпротивоположнымсобытиемпонимается
событие, которое обязательно должно произойти, если не наступило
некоторое событие.
Противоположные события несовместны и единственно возможны. Они
образуют полную группу событий. Например, если партия изготовленных
изделий состоит из годных и бракованных, то при извлечении одного
изделия оно может оказаться либо годным — событие, либо
бракованным — событие.

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности. 

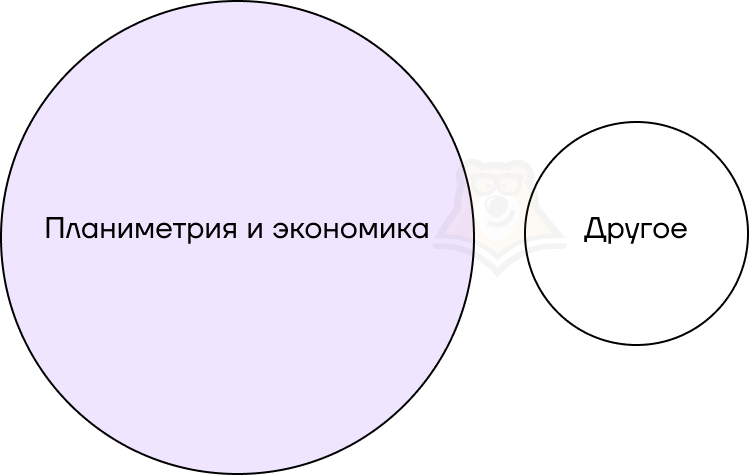
Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:\(P(A \cup B) = P(A) + P(B)\)

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: \(\frac{1}{6}\). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

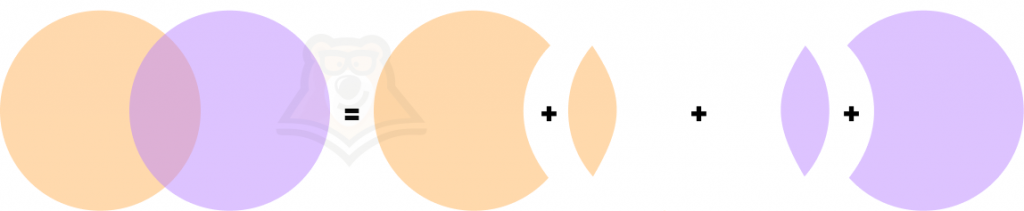
А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:\(P(A \cup B) = P(A) + P(B) — P(A \cap B)\)

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.