Математическое ожидание

Дисперсия

Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около её математического ожидания.

\ = M — (M)^2 \]

Дисперсия неслучайной величины

\ = 0 \]

Доказательство:

По определению дисперсии:

\ = M  = M^2 ] = M = M = 0\]

Дисперсия суммы случайных величин

\ = D + D + 2*cov(X,Y) \]

Доказательство:

Обозначим \(XY = Z \).

По теореме сложения математических ожиданий:

\ = M + M \]

Перейдем от случайных величин \(X, Y, Z \).  к соответствующим центрированным величинам \(\stackrel{ \circ }{X}, \stackrel{ \circ }{Y}, \stackrel{ \circ }{Z} \), имеем:

\

По определению дисперсии

\ = D = M = M + 2M + M \\
= D + 2 cov(X,Y) + D \]

Дисперсия произведения неслучайной величины на случайную

\ = a^2 D\]

Доказательство:

По определению дисперсии

\ = M)^2] = M)^2] = a^2 M)^2] = c^2 D \]

Доказательство:

Обозначим \(XY = Z \). По определению дисперсии

\ = D = M = M]^2\]

Так как величины \(XY\) независимы, то \(M = MM\) и

\ = MM)^2] \\

= M — 2MMM+ M^2M^2 \]

При независимых  \(XY\) величины  \(X^2Y^2\) также независимы, следовательно:

\  = M M, M = MM\]

и

\ = MM — M^2M^2 \]

но \(M^2\) есть не что иное, как второй начальный момент величины \(X\) , и, следовательно, выражается через дисперсию:

\ = D+M^2 \]

аналогично

\ = D+M^2 \]

Подставляя эти выражения и приводя подобные члены, приходим к формуле

Математическое ожидание и дисперсия непрерывной случайной величины

Для непрерывной случайной величины механическая интерпретация математического
ожидания сохранит тот же смысл: центр массы для единичной массы, распределённой непрерывно на оси
абсцисс с плотностью f(x). В отличие от дискретной случайной величиной, у которой
аргумент функции изменяется
скачкообразно, у непрерывной случайной величины аргумент меняется непрерывно. Но математическое ожидание
непрерывной случайной величины также связано с её средним значением.

Чтобы находить математическое ожидание и дисперсию непрерывной случайной величины,
нужно находить определённые интегралы. Если дана функция плотности непрерывной случайной величины, то
она непосредственно входит в подынтегральное выражение. Если дана функция распределения вероятностей, то,
дифференцируя её, нужно найти функцию плотности.

Арифметическое среднее всех возможных значений непрерывной случайной
величины называется её математическим ожиданием, обозначаемым
или .

Математическое ожидание
непрерывной случайной величины Х, плотностью вероятности которой является
функция f(x), находится как величина интеграла

,

если он сходится абсолютно.

Дисперсией непрерывной случайной величины называется величина интеграла

,

если он сходится.

Среднее квадратичное отклонение непрерывной случайной величины
определяется как арифметическое значение квадратного корня из дисперсии.

Ключевые особенности дисперсии

За дисперсию принято понимать средний квадрат отклонений полученных значений признака от среднего арифметического числа. Для обозначения используется одна заглавная латинская буква D.

Для правильного расчёта дисперсии необходимо посчитать разность между имеющимся числом и средним арифметическим, чтобы в итоге возвести результат в квадрат. Значений получится столько, сколько может быть реальных исходов у рассматриваемого события. После этого остаётся только просуммировать все полученные данные и разделить на количество элементов в последовательности. Если максимальное количество исходов приравнивается к 5, тогда делить нужно именно на эту цифру.

У дисперсии также есть свойства, которые обязательно нужно знать, чтобы решать различные математические задачи. К примеру:

• при увеличении случайной величины в Х раз, тогда дисперсия увеличится в Х раз;
• дисперсия никогда не бывает меньше нуля и не зависит от сдвига значений в большую или меньшую сторону.

К примеру: нужно представить, что был проведён 21 эксперимент и в итоге 7 разных исходов. Первым делом нужно рассчитать среднее арифметическое: сумма элементов равняется 21. Эту цифру нужно разделить на 7. В результате получится цифра 3. После этого из каждого числа исходной последовательности нужно вычесть 3. Каждое значение возводят в квадрат, а результат слаживают вместе. Если всё сделать правильно, то в итоге можно получить 12. На финальном этапе остаётся разделить число на количество элементов.

Актуальность применения медианы и моды

Математики склонны утверждать, что средние величины представляют собой своего рода отвлечённую величину. Отвлекаясь от определённых величин каждого варианта, эти числа отлично отображают общее положение, которое присуще всей совокупности единиц. В некоторых случаях можно наблюдать, что величина не имеет какого-либо равенства ни с одним из конкретных вариантов распространённых вариантов.

К примеру: среднее число членов одной семьи приравнивается к 4,85. Этот показатель был получен на основе исчисления соответствующей совокупности данных. Число не имеет ничего общего с определённым составом конкретной семьи, так как дробного числа членов семьи быть не может. В этом случае принято понимать за основу показатель средней величины состава семьи. Возле дробного числа группируются реальные варианты.

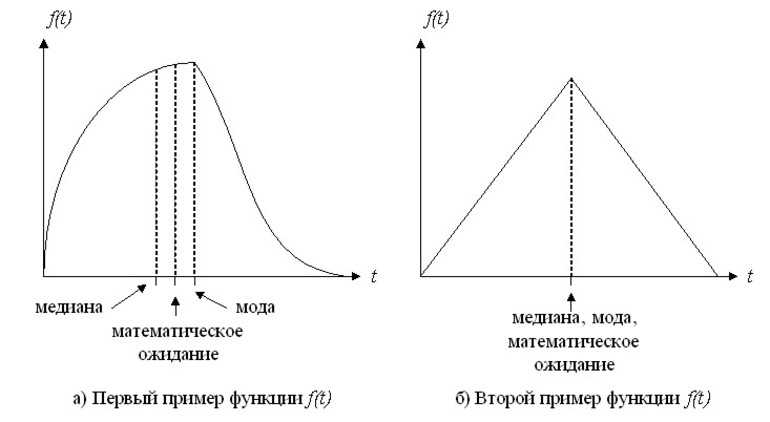
Когда стоит задача определить какую-либо абстрактную величину, тогда можно смело задействовать величины конкретных вариантов, содержащихся в рассматриваемой совокупности величин. Именно эти величины занимают определённое место в ранжированном ряду индивидуальных значений признака. Такими величинами чаще всего являются медиана, а также мода. Мода — это самая распространённая величина, которую принято обозначать символами Мо.

Мода как величина в прерывистом ряду всегда определяется на примере выявления самого большого процента мужчин, которые носят одинаковый размер обуви. После несложных математических действий можно понять, что большинство мужчин носят обувь 40 размера. А это значит, что Мо = 40, модой является сорок первый размер обуви.

А вот когда необходимо отыскать достоверную медиану, то первым делом нужно постараться найти один из центральных вариантов рассматриваемой совокупности. На примере изучаемого варианта за основу будет взят эксперимент, в котором участвовали 100 человек: 100:2 = 50. После этого по накопленным частотам выполняют определение достоверной величины пятидесятого ряда. Если следовать накопленной частотности, то полученная цифра будет находиться между 41 и 69 позициями. Это значит, что 50-й член ряда имеет величину 40 (Ме = 40-й размер обуви).

§ 2. Свойства математического ожидания

Во всех свойствах предполагается, что рассматриваемые существуют.

E1.

 Для произвольной

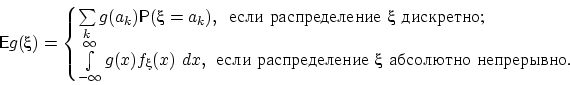
Доказательство.
Мы докажем это свойство (как и почти все дальнейшие) только для распределения.
Пусть
принимает значения с вероятностями

Тогда

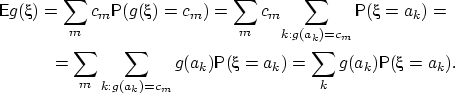
QED

Следствие 10.
Математическое ожидание существует тогда и только тогда, когда .

Доказательство.
Условием существование математического ожидания является
абсолютная сходимость ряда или интеграла
в определениях и .
По свойству это и есть условие при .

QED

E2.

 Математическое ожидание постоянной равно ей самой:
.

E3.

 Постоянную можно вынести за знак математического ожидания:

Доказательство
следует из свойства при .

QED

E4.

 Математическое ожидание суммы любых случайных величин
равно сумме их математических ожиданий, если только эти математические ожидания
существуют:

Доказательство.
Пусть случайные величины и имеют дискретные распределения со значениями
и соответственно.
Для борелевской функции можно доказать свойство, аналогичное (сделать это!).
Воспользуемся этим свойством для :

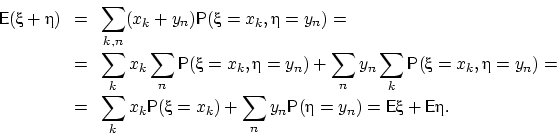
QED

E5.

 Если п.н., т.е. если , то .

Упражнение 42.
Доказать для и для распределений.

Замечание 18.
Сокращение «п.н.» читается как «почти наверное» и означает «с вероятностью 1».
По определению, математическое ожидание  это числовая характеристика распределения. Распределение
же не изменится от изменения случайной величины на множестве нулевой вероятности.
Поэтому, например, даже если не при всех , а на множестве единичной вероятности,
математическое ожидание всё равно неотрицательно.

E6.

 Если п.н., и при этом , то п.н., т.е. .

Доказательство. Это свойство мы докажем, заранее предполагая, что имеет дискретное распределение
с неотрицательными значениями . Равенство означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности нулевые, кроме вероятности,
соответствующей значению .

QED

Из свойств (E5) и (E6) вытекает множество полезных
утверждений:

Следствие 11.
Если п.н., то .

Следствие 12.
Если п.н., но , то п.н.

Следствие 13.
Если п.н., то .

E7.

 Математическое ожидание произведения независимых случайных
величин равно произведению их математических ожиданий:
если и независимы и их математические ожидания существуют, то

Доказательство. В дискретном случае:

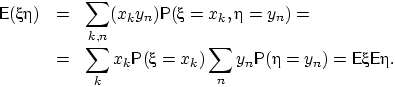
QED

Замечание 19.
Обратное утверждение к свойству (E7) неверно: из равенства не следует независимость величин и .

Пример 34.
Пусть принимает значения и с вероятностями по 1/3 каждое,
и . Это зависимые случайные величины:

Однако и , поэтому
.

Пример 35.
Пусть , и пусть и   заведомо зависимые случайные величины (доказать!).
Но математическое ожидание их произведения
равно произведению их математических ожиданий из-за симметричности распределений
, и относительно нуля. Действительно, по свойству
имеем:

N.Ch.

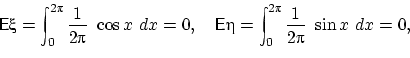
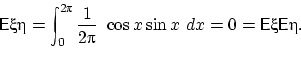
Краткое описание

Чтобы понять смысл условного математического ожидания случайной величины, необходимо изучить ряд правил, а также ознакомится с примерами, дабы в будущем можно было избежать грубых ошибок. Одной из важнейших числовых характеристик дискретной величины является матожидание. Для изучения всех нюансов необходимо ввести понятие системы случайных процессов. Если представить значение в виде графика, то итоговое ожидание будет выступать в виде некоторого центра массы, изображённой на графике фигуры. Для решения классической задачи можно задействовать следующую формулу: Е (х) = Х1О1 + Х1О2 + … + Х n О n.

Расшифровка формулы выглядит следующим образом:

• Е (х) — это точное значение матожидания величины Х.
• Ха — показатель величины случайного типа при конкретном исходе а.
• О — вероятность исхода а.
• n — количество возможных вариантов исходов.

В теории вероятности специалистам удалось доказать, что среднее значение постоянной величины даже после многочисленных испытаний всё равно будет стремиться к матожиданию. В некоторых случаях результат может быть отрицательный. А это значит, что если количество итоговых испытаний слишком велико, то среднее значение обязательно будет равно матожиданию (прогноз среднего значения). Для более тщательного изучения темы специалисты рекомендуют использовать следствие (теорема с небольшим доказательством, которое следует из другой теоремы).

Гораздо проще разобраться в этой теме в том случае, если изучить наглядный пример. Если человек несколько раз бросит самый обычный шестигранный игральный кубик, и будет записывать все выпавшие значения, то при большом количестве испытаний можно получить число 3,5. Аналогичный результат будет достигнут и в том случае, если просчитать матожидание. Подсчёт выглядит следующим образом:

• Р1 = Р2 … = Р6 = 1/6. Это число указывает на вероятность выпадения одной из граней игрального кубика и все они равны, так как у качественного кубика вероятность выпадения каждой грани абсолютно одинаковая.
• Ха = а — формула указывает на то число, которое может выпасть на кубике.
• n = 6 — точное число граней кубика либо количество вариантов.

Свойства математического ожидания

Рассмотрим свойства математического ожидания.

Свойство 1. Математическое ожидание постоянной
величины равно этой постоянной:

Свойство 2. Постоянный множитель можно выносить за знак
математического ожидания:

Свойство 3. Математическое ожидание суммы (разности)
случайных величин равно сумме (разности) их математических ожиданий:

Свойство 4. Математическое ожидание произведения случайных
величин равно произведению их математических ожиданий:

Свойство 5. Если все значения случайной величины
X уменьшить (увеличить) на одно и то же число С, то её
математическое ожидание уменьшится (увеличится) на то же число:

Доступное программное обеспечение

Из всех перечисленных правил и формул можно сделать вывод, что используемое математическое ожидание обозначается самым простым образом, но в этой теме нужно хорошо разбираться. Правильные расчёты дисперсии и математического ожидания — это не самая простая задача, с арифметической точки зрения.

Чтобы не тратить драгоценное время на поиски решения можно воспользоваться специальной онлайн-калькулятор, которая активно используется в высших учебных заведениях. Это программное обеспечение носит название R. В ней предусмотрено наличие специальных функций, которые позволяют рассчитать значения для многих понятий из статистики и теории вероятности.

К примеру: пользователь может указать конкретный вектор значений. Это делается следующим образом: vector <— c (1,5,2…). Как только нужно будет посчитать какие-либо значения для этого вектора, следует вписать функцию и задать его в качестве аргумента. Для поиска дисперсии необходимо отыскать функцию var. После этого остаётся только нажать «ввод» и результат отобразится на экране.

Из всей описанной информации можно сделать вывод, что математическое ожидание и дисперсия — это классические понятия, которые широко распространены в теории вероятности. Без изучения этой темы учащемуся будет сложно что-либо рассчитать и получить желаемый результат. В базовом курсе лекций в высших учебных заведениях эти два понятия рассматриваются уже в первый месяц изучения теории вероятности. Непонимание этих простейших понятий и неспособность решать элементарные задачи чревато тем, что многие студенты попросту начинают отставать от учебной программы. А это заканчивается плохими оценками по результатам сессии.

Математическое ожидание дискретной случайной величины

Подойдём к понятию математического ожидания. Пусть масса некоторого вещества
распределена между точками оси абсцисс .
При этом каждая материальная точка имеет соответствующую ей массу с вероятностью из .
Требуется выбрать одну точку на оси абсцисс, характеризующую положение всей системы материальных точек,
с учётом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Это
есть среднее взвешенное значение случайной величины X, в которое абсцисса каждой точки
входит с «весом», равным соответствующей
вероятности. Полученное таким образом среднее значение случайной величины X называется её
математическим ожиданием.

Математическим ожиданием дискретной случайной величины называется сумма произведений
всех возможных её значений на вероятности этих значений:

Пример 1. Организована беспроигрышная лотерея.
Имеется 1000 выигрышей, из них 400 по 10 руб. 300 — по 20 руб. 200 — по 100 руб. и 100 —
по 200 руб. Каков средний размер выигрыша для купившего один билет?

Решение. Средний выигрыш мы найдём, если общую сумму выигрышей,
которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая
сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта
среднего выигрыша можно представить и в следующем виде:

С другой стороны, в данных условиях размер выигрыша является
случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с
вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый
средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.

Пример 2. Издатель решил издать новую книгу. Продавать книгу
он собирается за 280 руб., из которых 200 получит он сам, 50 — книжный магазин и 30 — автор. В таблице
дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги.

Число проданных экземпляров	Вероятность	Затраты
500	0,20	225000
1000	0,40	250000
2000	0,25	300000
3000	0,10	350000
4000	0,05	400000

Найти ожидаемую прибыль издателя.

Решение. Случайная величина «прибыль» равна разности доходов от продажи и стоимости затрат.
Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а
затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей
таблице обобщены ожидаемые значения случайной величины — прибыли:

Число	Прибыль	Вероятность
500	-125000	0,20	-25000
1000	-50000	0,40	-20000
2000	100000	0,25	25000
3000	250000	0,10	25000
4000	400000	0,05	20000
Всего:		1,00	25000

Таким образом, получаем математическое ожидание прибыли издателя:

.

Пример 3. Вероятность попадания при одном выстреле .
Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5.

Решение. Из всё той же формулы математического ожидания, которую мы использовали до
сих пор, выражаем — расход снарядов:

.

Математическое ожидание дискретной случайной величины

Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина  принимает значения  с вероятностями  соответственно. Тогда математическое ожидание  данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

Вычислим, например, математическое ожидание случайной величины  – количества выпавших на игральном кубике очков:

 очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

Пример 4

Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины  – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

Пример 5

Случайная величина  задана своим законом распределения вероятностей:

Найти , если известно, что . Выполнить проверку.

Есть?

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

Решения и ответы:

Пример 3. Решение: по условию  – вероятность попадания в мишень. Тогда: – вероятность промаха.

Составим  – закон распределения попаданий при двух выстрелах:

 – ни одного попадания. По теореме умножения вероятностей независимых событий:

 – одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

 – два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ

Примечание: можно было использовать обозначения  – это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: Вычислим математическое ожидание: Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания: поменяем части местами и проведём упрощения:таким образом:

Выполним проверку:, что и требовалось проверить.

Ответ

(Переход на главную страницу)

Определение[]

Пусть задано вероятностное пространство (Ω,F,P){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )} и определённая на нём случайная величина X{\displaystyle X}. То есть, по определению, XΩ→R{\displaystyle X:\Omega \to \mathbb {R} } — измеримая функция. Тогда, если существует интеграл Лебега от X{\displaystyle X} по пространству Ω{\displaystyle \Omega }, то он называется математическим ожиданием, или средним значением и обозначается EX{\displaystyle \mathbb {E} X}.

EX≡∫ΩX(ω)P(dω).{\displaystyle \mathbb {E} X\equiv \int \limits _{\Omega }X(\omega )\,\mathbb {P} (d\omega ).}

Зависимость итога от количества экспериментов

Эксперты утверждают, что при правильном расчёте дисперсии в знаменателе может стоять одно из двух предложенных чисел: N или N -1. На точное число проведённых экспериментов указывает запись N. Если итоговое количество испытаний измеряется сотнями, то в знаменателе должно стоять только N. Ну а если единицами, то N -1. Учёные решили провести весьма символическую границу между этими двумя показателями, так как на сегодняшний день она достигает цифры 30. Если же количество экспериментов не достигло этой отметки, то делить сумму нужно только на N-1, а если больше — то на N.

Многочисленные свойства математического ожидания очень важны для правильного решения поставленных задач. Для изучения этой темы необходимо знать, что собой представляет квадратическое отклонение. Для обозначения этого термина используются буквы sd, либо греческая строчная «сигма». Квадратическое отклонение отображает то, насколько именно отклоняются значения от центрального признака. Если в основе лежит нахождение нужного значения, тогда следует постараться правильно рассчитать квадратный корень из дисперсии.

Можно построить график равномерного распределения, чтобы непосредственно на нём увидеть реальную величину среднего квадратного отклонения. Для этих целей необходимо выполнить несколько несложных заданий. Нужно взять половину изображения справа и слева от моды (центральное значение), дабы постараться провести перпендикуляр к горизонтальной оси так, чтобы площади получившихся фигур были абсолютно равными.