Вычисление тригонометрических функций числа
В данном пункте рассмотрим случай, когда определение рассматриваемых нами функций тригонометрии, происходит из числового значения, а не угла. Таких подходов два:
- Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону.
- На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки.
- Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.
В связи с этим выделяют следующие функции:
- (sin f = y) Синус числа f- определяется ординатой точки единичной окружности, которая равна числу f;
- (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f;
- (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
А что насчет тангенсов и котангенсов?
На самом деле, для них тоже есть свои оси, правда они имеют немного специфический вид:
В остальном же способ обращения с ними будет такой же, как с синусом и косинусом.
Напоследок рекомендую тебе самостоятельно решить вот этот пример, прибегая к помощи единичной окружности
Дано уравнение \( \displaystyle 2co{{s}^{2}}x+2sin2x=3\). Решите данное уравнение. Укажите корни данного уравнения, принадлежащие промежутку \( \displaystyle \left\).
Решение:
\( \displaystyle tgx=1\), \( \displaystyle x=\frac{\pi }{4}+\pi n\)
\( \displaystyle tgx=\frac{1}{3}\), \( \displaystyle x=arctg\frac{1}{3}+\pi n\)
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°
Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
График тангенса
Так как тангенс обладает периодом, равным π, достаточно построить его график на каком-нибудь промежутке длиной π. Далее его можно будет просто перенести на π единиц влево и вправо. Удобно выбрать промежуток от – π/2 до π/2. Дело в том, что на нем она определена во всех точках, кроме его концов.
Через точки х = – π/2 и х = π/2 проведем штриховые линии – они означают, что график НЕ должен пересекать их. Ясно, что график проходит через точку (0; 0), ведь tg 0 = 0. Тангенс представляет собой дробь sinx/cosx. При увеличении х от 0 до π/2 знаменатель возрастает, а числитель убывает, стремясь к нулю. Поэтому вся дробь неограниченно растет, и график тангенса возрастает до бесконечности:
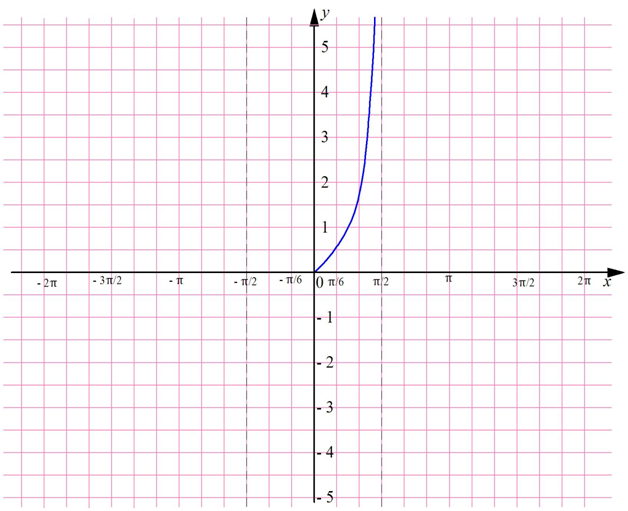
Так как мы строим график нечетной ф-ции, то мы можем полученную ветвь отобразить симметрично относительно начала координат:
Полученный график называют тангенсоидой. Осталось воспользоваться тем, что мы рассматриваем периодическую ф-цию с периодом π, и перенести тангенсоиду влево и вправо:
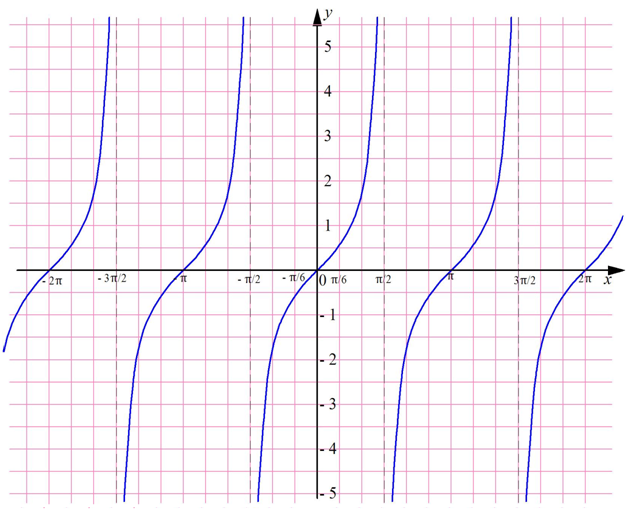
Котангенс угла
Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:
Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:
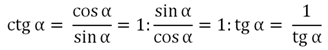
Почти во всех задачах с помощью формулы
можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.
Значения этой ф-ции рассчитываются так:
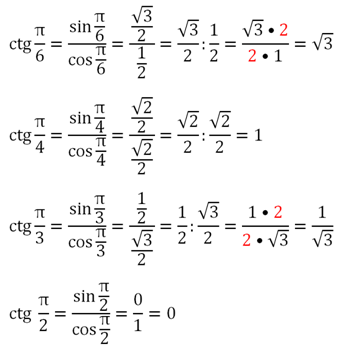
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.
График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:
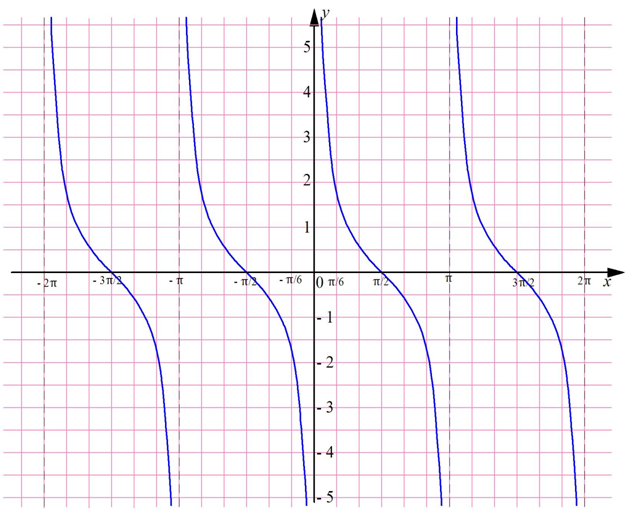
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.
Для сравнения покажем на одной плоскости графики тангенса и котангенса:
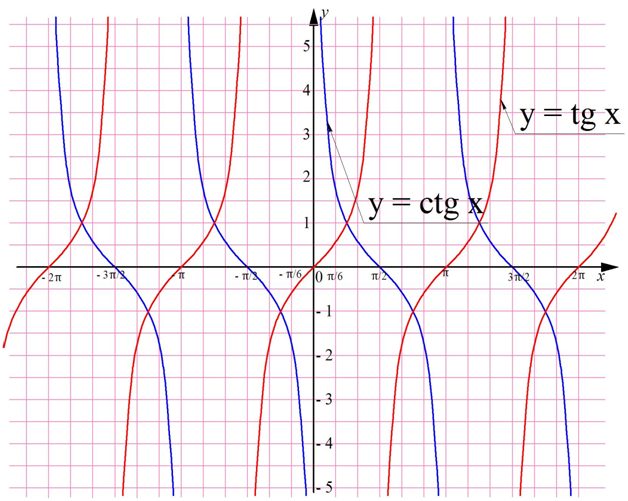
Котангенс, как и тангенс – нечетная ф-ция, то есть
ctg (– x) = – ctgx
Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.
Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.
Синус, косинус, тангенс и котангенс на тригонометрической окружности
Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!
Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.
Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?
Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.
Совместим мы их вот так:
Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной \( 1\). Это так потому, что окружность-то у меня единичная!
Тогда по определению синуса и косинуса:
- \( sin\ \alpha =\frac{AB}{OB}=\frac{AB}{1}=AB\)
- \( cos\ \alpha =\frac{OA}{OB}=\frac{OA}{1}=OA\)
А что же такое отрезки \( OA\) и \( OB\)? Чему равны их длины?
Смотри, сейчас будет самое главное: мы взяли угол \( \alpha \) и провели луч, соединяющий этот угол с точкой на окружности.
Обозначим эту точку через \( B\). Пусть \( B\) имеет координаты \( B\left( x,y \right)\).
Тогда длина отрезка \( OA\) равна \( x\), а длина отрезка \( AB\)–равна \( y\).
Но мы с тобой помним, что \( sin\ \alpha =AB\), \( cos\ \alpha =OA\), тогда:
- \( y=sin\ \alpha \)
- \( x=cos\ \alpha \)
Ух ты! Это надо еще раз обдумать, что же мы такое получили.
Давай проговорим еще раз: мы выбрали некоторый угол \( \alpha \) и хотим найти его синус и косинус.
Что мы делаем?
- Проводим единичную окружность с центром, совпадающим с вершиной угла;
- Ищем точку пересечения нашего угла с окружностью;
- Её «иксовая» координата – это косинус нашего угла;
- Её «игрековая» координата – это синус нашего угла.
Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус \( 30\) градусов.
Отмечаем \( 30\) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).
Как найти \( x\) и \( y\)?
Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в \( 30\) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).
Так как гипотенуза равна \( 1\), то противолежащий ей катет равен \( 0,5\), откуда:
\( sin\ 30{}^\circ =0,5\)Что касается косинуса: для этого нам потребуется заметить, что выполняется тривиальное утверждение (основное тригонометрическое тождество):
\( si{{n}^{2}}\alpha +co{{s}^{2}}\alpha =1\)Как ты думаешь, откуда оно берется? Да это же пресловутая теорема Пифагора!
Наши катеты в треугольничке равны \( x\) и \( y\), которые в свою очередь совпадают с \( cos\ \alpha \) и \( sin\ \alpha \). Гипотенуза в треугольнике равна \( 1\).
Тогда:
\( {{x}^{2}}+{{y}^{2}}=1\) или, что то же самое,\( si{{n}^{2}}\alpha +co{{s}^{2}}\alpha =1\)Эта формула позволит по известному синусу вычислить неизвестный косинус и наоборот.
В частности, если:
\( si{{n}^{2}}30{}^\circ +co{{s}^{2}}30{}^\circ =1\) и \( sin\ 30{}^\circ =0,5\), то
\( \frac{1}{4}+co{{s}^{2}}30{}^\circ =1\)\( \displaystyle co{{s}^{2}}30{}^\circ =\frac{3}{4}\)\( \displaystyle cos\ 30{}^\circ =\pm \sqrt{\frac{3}{4}}=\pm \frac{\sqrt{3}}{2}\)
Два случая, когда тригонометрическая окружность может пригодиться для решения уравнений
- В ответе у нас не получается «красивый» угол, но тем не менее надо производить отбор корней
- В ответе получается уж слишком много серий корней
Тему «тригонометрические уравнения» я старался писать, не прибегая к окружности. Многие бы меня за такой подход не похвалили.
Но мне милее формулы, уж что тут поделать. Однако в некоторых случаях формул оказывается мало. Например здесь:
Решите уравнение: \( \displaystyle 8co{{s}^{4}}x-10co{{s}^{2}}x+3=0\)
Решение:
Ну что же. Решить само уравнение несложно.
Замена \( \displaystyle t=co{{s}^{2}}x\).
Корни:
Обратная замена:
\( \displaystyle co{{s}^{2}}x=\frac{1}{2}\), откуда
\( \displaystyle cosx=\frac{\sqrt{2}}{2}~\) или \( \displaystyle cosx=-\frac{\sqrt{2}}{2}\)
Или же:
Откуда
\( \displaystyle cosx=\frac{\sqrt{3}}{2}\) или \( \displaystyle cosx=-\frac{\sqrt{3}}{2}\)
Отсюда наше исходное уравнение равносильно аж четырем простейшим уравнениям!
Понятие угла: радиан, градус
Давай для начала разберёмся в понятии угла.
Посмотрим на рисунок.
Вектор \( AB\) «повернулся» относительно точки \( A\) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).
Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в \( 1{}^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac{1}{360}\) части окружности.
Таким образом, вся окружность состоит из \( 360\) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен \( 360{}^\circ \).
То есть на рисунке выше изображён угол \( \beta \), равный \( 50{}^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac{50}{360}\) длины окружности.
Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
Ну что, разобрался? Если нет, то давай разбираться по рисунку.
Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.
То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).
Таким образом, длина дуги вычисляется по формуле:
\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.
Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?
Да, для этого надо вспомнить формулу длины окружности. Вот она:
\( L=2\pi \cdot r\)Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).
То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360{}^\circ \).
Соответственно, \( \pi =180{}^\circ \).
Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.
А сколько радиан составляют \( 60{}^\circ \)?
Всё верно \( \frac{\pi }{3}\)!Уловил? Тогда вперёд закреплять:\( 36{}^\circ =?\)\( \frac{\pi }{2}=?\)\( 30{}^\circ =?\)\( \frac{\pi }{4}=?\)\( 90{}^\circ =?\)\( \frac{2\pi }{3}=?\)\( 45{}^\circ =?\)\( 20{}^\circ =?\)\( \frac{\pi }{6}=?\)\( 10{}^\circ =?\)\( \frac{\pi }{9}=?\)\( 3\pi =?\)\( 720{}^\circ =?\)Возникли трудности?
Отрицательные углы
Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:
Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.
Мы шли от положительного направления оси \( \displaystyle Ox\) против часовой стрелки:
Тогда на нашем рисунке построен угол, равный \( \displaystyle 180+45=225{}^\circ \). Аналогичным образом мы строили все углы.
Однако ничего нам не запрещает идти от положительного направления оси \( \displaystyle Ox\) по часовой стрелке.
Мы будем тоже получать различные углы, но они будут уже отрицательными:
А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:
В целом правило можно сформулировать вот так:
- Идем против часовой стрелки – получаем положительные углы
- Идем по часовой стрелке – получаем отрицательные углы
Схематично правило изображено вот на этом рисунке:
Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.
Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.
Посмотри на следующую картинку:
Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.
Что мы с тобой видим? А вот что:
Тогда если \( \displaystyle \text{sin}\ \text{ }\!\!\alpha\!\!\text{ }=\text{y}\),
то \( \displaystyle \sin \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{y}\)
\( \displaystyle \sin \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{sin}\ \text{ }\!\!\alpha\!\!\text{ }\).
Тогда если \( \displaystyle \text{cos}\ \text{ }\!\!\alpha\!\!\text{ }=\text{x}\),то и \( \displaystyle \cos \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\text{x}\)\( \displaystyle \cos \left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\text{cos}\ \text{ }\!\!\alpha\!\!\text{ }\)Так как \( \displaystyle \text{tg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\frac{\text{sin}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}{\text{cos}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}=\frac{-\text{sin}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}{\text{cos}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}\), то:\( \displaystyle \text{tg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{tg }\!\!\alpha\!\!\text{ }\)Так как \( \displaystyle \text{ctg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=\frac{\text{cos}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}{\text{sin}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)}=\frac{\text{cos}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}{-\text{sin}\left( \text{ }\!\!\alpha\!\!\text{ } \right)}\), то:
\( \displaystyle \text{ctg}\left( -\text{ }\!\!\alpha\!\!\text{ } \right)=-\text{ctg}\ \text{ }\!\!\alpha\!\!\text{ }\)Таким образом, мы всегда можем избавиться от отрицательного знака внутри любой тригонометрической функции: либо просто уничтожив его, как у косинуса, либо поставив его перед функцией, как у синуса, тангенса и котангенса.
Кстати, вспомни-ка, как называется функция \( \displaystyle f(x)\), у которой для любого допустимого \( \displaystyle x\) выполняется:\( \displaystyle f(-x)=-f(x)\)?
Такая функция называется нечетной.
А если же для любого допустимого \( \displaystyle x\) выполняется: \( \displaystyle f(-x)=f(x)\)? То в таком случае функция называется четной.
Таким образом, мы с тобой только что показали, что:
Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.
С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.
Можно ли это сделать? Конечно, можно!
У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)
Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.
Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:
Таблица функций тригонометрии
Эта таблица представляет из себя уже посчитанные значения sin, cos, tg, ctg углов от 0до 360 градусов. Такая таблица заменит специальный калькулятор если нужны значения, нужно просто найти нужный угол в таблице.
Области применения тригонометрии
Приведём для примера несколько областей в которых применяются функций:
- В астрономии. Во-первых, как отмечалось выше область астрономии стала первой, где стали применять тригонометрические функции. Именно по этой причине довольно долго этот раздел науки относили к астрономии. Одним из крупных открытий в этой науке при помощи тригонометрических основ стала возможность вычисления наступления темноты, а также составление первых звёздных карт.
- В физике. Мир, который нас окружает построен на колебательных процессах, это такие явления и процессы, которые повторяются через определённый цикл;
- В окружающей нас природе. Например, отражение лучей солнца от различных поверхностей;
- В медицине. К примеру, существует такое понятие как формула сердца;
- В биологии. Биологические ритмы, модель которых строят при помощи тригонометрии;
- В музыке, звуковые ритмы, построение моделей.
- Важную роль тригонометрия играет и для морского флота и авиации;
- В изучении сейсмической активности.
Как мы видим тригонометрия очень важная наука, которая пронизывает практически все сферы нашей жизни.
Функция y = sin x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
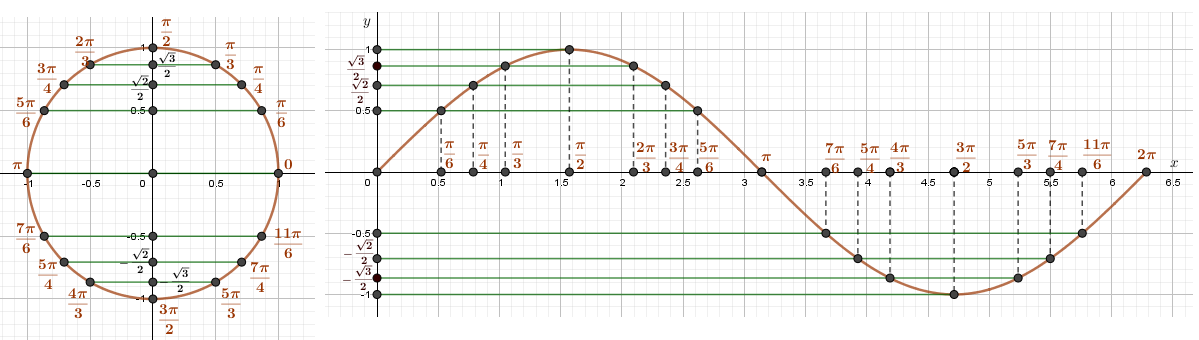
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .Часть синусоиды для 0≤x≤2π называют волной синусоиды .Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .
п.2. Свойства функции y=sinx
1. Область определения \(x\in\mathbb\) — множество действительных чисел.
2. Функция ограничена сверху и снизу
Область значений \(y\in\)
3. Функция нечётная
4. Функция периодическая с периодом 2π
5. Максимальные значения \(y_=1\) достигаются в точках
Минимальные значения \(y_=-1\) достигаются в точках
Нули функции \(y_=sinx_0=0\) достигаются в точках \(x_0=\pi k\)
6. Функция возрастает на отрезках
$$ -\frac\pi2+2\pi k\leq x\leq\frac\pi2+2\pi k $$
Функция убывает на отрезках
$$ \frac\pi2+2\pi k\leq x\leq\frac+2\pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке: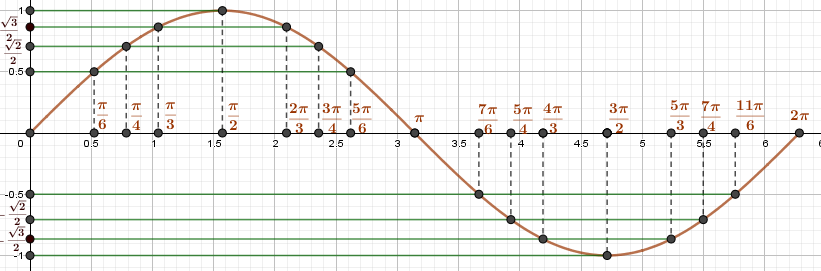
a) \(\left\) $$ y_=sin\left(\frac\pi6\right)=\frac12,\ \ y_=sin\left(\frac\pi2\right)=1 $$ б) \(\left\) $$ y_=sin\left(\frac\right)=-1,\ \ y_=sin\left(\frac\right)=\frac12 $$
Пример 2. Решите уравнение графически:a) \(sinx=3x\)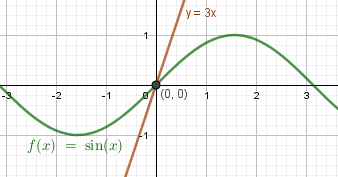
Один корень: x = 0
б) \(sinx=2x-2\pi\)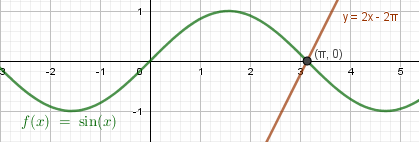
Один корень: x = π
в) \(sinx-\sqrt=0\)\(sinx=\sqrt\)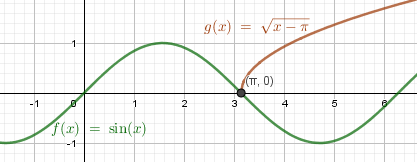 
Один корень: x = π
г*) \(sinx=\left(x-\frac\pi2\right)^2-\frac\)\(y=\left(x-\frac\pi2\right)^2-\frac\) – парабола ветками вверх, с осью симметрии \(x_0=\frac\pi2\) и вершиной \(\left(\frac\pi2; -\frac\right)\) (см. §29 справочника для 8 класса)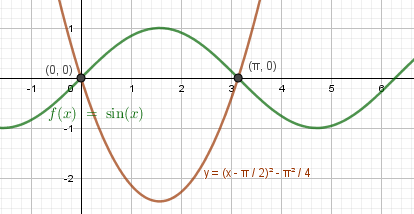
Два корня: \(x_1=0,\ \ x_2=\pi\)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx,\ \ y=-sinx,\ \ y=2sinx,\ \ y=sinx+2 $$ 
\(y=-sinx\) – отражение исходной функции \(y=sinx\) относительно оси OX. Область значений \(y\in\).\(y=2sinx\) – исходная функция растягивается в 2 раза по оси OY. Область значений \(y\in\).\(y=sinx+2\) — исходная функция поднимается вверх на 2. Область значений \(y\in\).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx,\ \ y=sin2x,\ \ y=sin\frac $$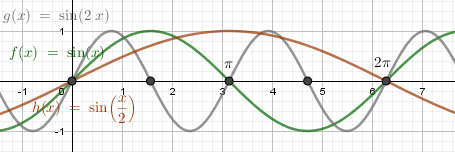 
Амплитуда колебаний у всех трёх функций одинакова, область значений \(y\in\).Множитель под синусом изменяет период колебаний.\(y=sin2x\) — период уменьшается в 2 раза, полная волна укладывается в отрезок \(0\leq x\leq \pi\).\(y=sin\frac\) — период увеличивается в 2 раза, полная волна укладывается в отрезок \(0\leq x\leq 4\pi\).