Материальная точка. система отсчета

Положение предметов в пространстве. Тело отсчета.

Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: «слева от…», «над …» и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.

Местонахождение клада: «Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота». Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета

То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение

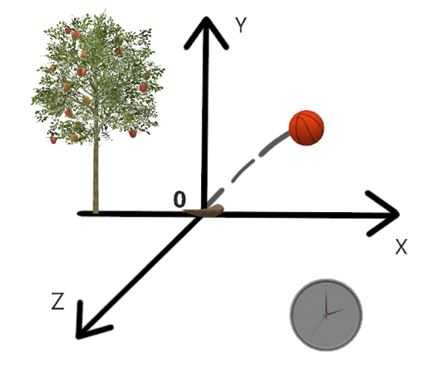Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку. Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как  материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см

рисунок 8). Радиус-вектор, проведенный в точку A обозначим r, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

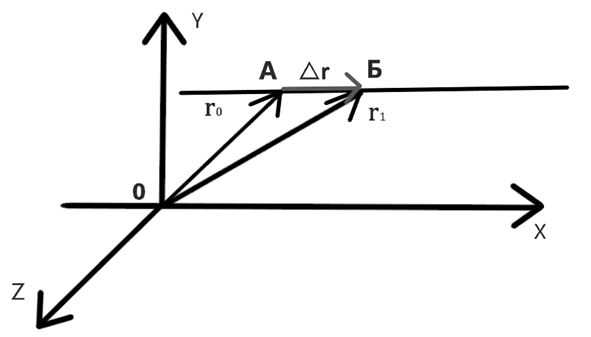
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r= r + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z– это компоненты изначальных векторов r и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;
r_y = r_0y + v_y*t;
r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х) и конечной (х₁) точки на ось ОХ.

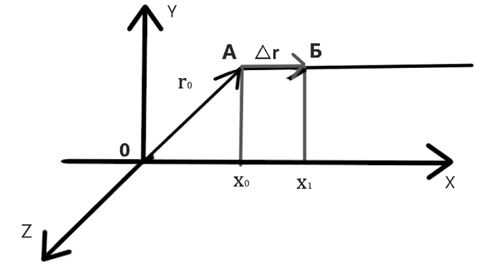Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x+ v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S + v*t.

Если точка начала двигаться из начала отсчета S = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x+ v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x- v*t = 0,03 — 5*t.

Упражнения

Упражнение №1

Можно ли считать автомобиль материальной точкой в следующих уловиях:а) при определении пути, который он прошел за $2 \space ч$, двигаясь со средней скоростью, равной $80 \frac{км}{ч}$;б) при обгоне им другого автомобиля?

Посмотреть ответ

Скрыть

Ответ:

В первом случае за указанное время автомобиль пройдет путь:$s = \upsilon_{ср} t$,$s = 80 \frac{км}{ч} \cdot 2 \space ч = 160 \space км$.

Очевидно, что такое расстояние намного больше размеров самого автомобиля. Поэтому в данном случае мы можем рассматривать его как материальную точку.

Во втором случае (когда автомобиль идет на обгон) мы не можем считать его материальной точкой. Ведь в этом случае для нас будут важны габариты автомобиля и движение отдельных его точек.

Упражнение №2

Самолет совершает перелет из Москвы во Владивосток. Может ли рассматривать самолет как материальную точку диспетчер, наблюдающий за его движением; пассажир этого самолета?

Посмотреть ответ

Скрыть

Ответ:

Диспетчер, являющийся телом отсчета, может рассматривать самолет как материальную точку, потому что размеры самолета намного меньше пролетаемого им расстояния.

А вот пассажир самолета не может принимать его за материальную точку, ведь он движется вместе с ним.

Упражнение №3

Когда говорят о скорости машины, поезда и других транспортных средств, тело отсчета обычно не указывают. Что подразумевают в этом случае под телом отсчета?

Посмотреть ответ

Скрыть

Ответ:

В случаях, когда речь идет о скоростях транспортных средств, под телом отсчета обычно подразумевают земную поверхность или любое тело, находящееся в состоянии покоя относительно Земли.

Упражнение №4

Мальчик стоял на земле и наблюдал, как его младшая сестра каталась на карусели. После катания девочка сказала брату, что и он сам, и дома, и деревья быстро проносились мимо нее. Мальчик же стал утверждать, что он вместе с домами и деревьями был неподвижен, а двигалась сестра. Относительно каких тел отсчета рассматривали движение девочка и мальчик? Объясните, кто прав в споре.

Посмотреть ответ

Скрыть

Ответ:

Наблюдающий за каруселью мальчик рассматривал движение карусели относительно поверхности Земли. Так, ни деревья, ни дома, ни сам мальчик не двигались относительно друг друга. Двигались только карусель и девочка на ней.

Девочка же рассматривала движение относительно своего сиденья карусели. Поэтому для нее в движении находились все остальные окружающие предметы (деревья, дома и др.)

Получается, что в этом споре правы оба. Просто брат с сестрой рассматривали движение относительно разных тел отсчета.

Упражнение №5

Относительно какого тела отсчета рассматривают движение, когда говорят: 

• скорость ветра равна $5 \frac{м}{с}$;
• бревно плывет по течению реки, поэтому его скорость равна нулю;
• скорость плывущего по реке дерева равна скорости течения воды в реке;
• любая точка колеса движущегося велосипеда описывает окружность;
• Солнце утром восходит на востоке, в течение дня движется по небу, а вечером заходит на западе?

Посмотреть ответ

Скрыть

Ответ:

• скорость ветра оценивают относительно поверхности Земли;
• плывущее бревно рассматривают относительно поверхности реки, которая сама находится в движении;
• дерево плывет со скоростью течения воды в реке, если рассматривать его движение относительно берега;
• точки колеса велосипеда движутся по окружности относительно самого велосипеда;
• движение Солнца по небу рассматривается относительно линии горизонта.

Движение по окружности с постоянной по модулю скоростью

Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.

Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ​\( a_{цс} \)​, единицы измерения – ​м/с2​.

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.Период – это время, за которое тело совершает один полный оборот.
Обозначение – ​\( T \)​, единицы измерения – с.

где ​\( N \)​ – количество оборотов, ​\( t \)​ – время, за которое эти обороты совершены.Частота вращения – это число оборотов за единицу времени.
Обозначение – ​\( \nu \)​, единицы измерения – с–1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ​\( v \)​, единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ​\( \omega \)​, единицы измерения – рад/с .

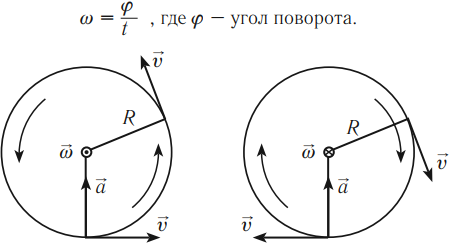
Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к

радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:

Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:

Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ​\( v_1 \)​, и все точки обода колеса движутся относительно его центра с такой же линейной скоростью \( v_1 \), то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ​\( (m) \)​ равна нулю, мгновенная скорость в верхней точке ​\( (n) \)​ равна удвоенной скорости ​\( v_1 \)​, мгновенная скорость точки ​\( (p) \)​, лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ​\( (c) \)​ – по теореме косинусов.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​\( a \)​, единица измерения — м/с2.
В векторном виде:

где ​\( v \)​ – конечная скорость; ​\( v_0 \)​ – начальная скорость;
​\( t \)​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​\( a_n \)​ – нормальное ускорение, ​\( a_{\tau} \)​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, ​\( v \)​ ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности

Механическое движение способы описания движения система отсчета материальная точка

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Сложное движение точки

Сложное движение точки

– это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат. Такое движение также называют составным движением точки.

Абсолютное движение точки

– это движение точки относительно неподвижной системы координат.

Переносное движение точки

– это движение точки, вызванное движением подвижной системы координат относительно неподвижной.

Относительное движение точки

– это движение точки относительно подвижной системы координат.

Для описания сложного движения, мы выбираем неподвижную (основную) систему координат и подвижную . Будем считать, что подвижная система связана с некоторым движущимся твердым телом, относительно которого, в свою очередь движется точка. Например, человек, идущий в движущемся вагоне. Здесь неподвижная система координат – это система, связанная с рельсами и ландшафтом. Твердое тело – вагон. Точка – человек. Подвижная система координат – система, связанная с вагоном. Абсолютное движение – движение человека относительно рельс; относительное движение – движение человека относительно вагона; переносное движение – движение вагона относительно рельс.

Абсолютная скорость (ускорение) точки

– это скорость (ускорение) точки в неподвижной системе координат.

Переносная скорость (ускорение) точки

– это скорость (ускорение) той точки подвижной системы координат, в которой, в данный момент времени, находится точка, совершающая сложное движение.

Относительная скорость (ускорение) точки

– это скорость (ускорение) точки относительно подвижной системы координат.

Теорема о сложении скоростей При составном движении абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:. Модуль абсолютной скорости: . Эту теорему также называют правилом параллелограмма или треугольника скоростей.

Теорема Кориолиса о сложении ускорений При составном движении, абсолютное ускорение точки равно векторной сумме переносного , относительного и кориолисова (поворотного) ускорений:, где – ускорение Кориолиса (кориолисово ускорение); – угловая скорость вращения подвижной системы координат.

Кориолисово ускорение также называют поворотным ускорением. Оно характеризует изменение направления относительной скорости точки, вызванное вращением подвижной системы координат. Если переносное движение является поступательным, то , кориолисово ускорение равно нулю.

Основные понятия кинематики.

Пусть за интервал времени от t1 до t2 материальная точка переместилась из положения 1 в положение 2. О — начало отсчёта. r1 и r2 — радиусы-векторы точки в моменты времени t1 и t2 соответственно. l — траектория материальной точки. S — путь, пройденный материальной точкой за интервал времени от t1 до t2.

Перемещение материальной точки за интервал времени от t₁ до t₂:

Перемещение материальной точки за интервал времени от t=t₁ до t=t₂
— это вектор, проведенный из её положения в момент времени t₁ в её положение в момент времени
t₂.

Траектория материальной точки — это линия, которую она описывает при своём движении.

Длина пути S — это сумма длин всех участков траектории, пройденных материальной точкой за
рассматриваемый промежуток времени.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. В состав системы отсчёта входят

1) только тело отсчёта 2) только тело отсчёта и система координат 3) только тело отсчёта и часы 4) тело отсчёта, система координат, часы

2. Относительной величиной является: А. Путь; Б. Перемещение. Правильный ответ

1) только А 2) только Б 3) и А, и Б 4) ни А, ни Б

3. Пассажир метро стоит на движущемся вверх эскалаторе. Он неподвижен относительно

1) пассажиров, стоящих на другом эскалаторе, движущемся вниз 2) других пассажиров, стоящих на этом же эскалаторе 3) пассажиров, шагающих вверх по этому же эскалатору 4) светильников на баллюстраде эскалатора

4. Относительно какого тела покоится автомобиль, движущийся по автостраде?

1) относительно другого автомобиля, движущегося с такой же скоростью в противоположную сторону 2) относительно другого автомобиля, движущегося с такой же скоростью в ту же сторону 3) относительно светофора 4) относительно идущего вдоль дороги пешехода

5. Два автомобиля движутся с одинаковой скоростью 20 м/с относительно Земли в одном направлении. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0 2) 20 м/с 3) 40 м/с 4) -20 м/с

6. Два автомобиля движутся с одинаковой скоростью 15 м/с относительно Земли навстречу друг другу. Чему равна скорость одного автомобиля в системе отсчёта, связанной с другим автомобилем?

1) 0 2) 15 м/с 3) 30 м/с 4) -15 м/с

7. Какова относительно Земли траектория точки лопасти винта летящего вертолёта?

1) прямая 2) окружность 3) дуга 4) винтовая линия

8. Мяч падает с высоты 2 м и после удара о пол поднимается на высоту 1,3 м. Чему равны путь ​ \( l \) ​ и модуль перемещения ​ \( s \) ​ мяча за всё время движения?

1) \( l \) = 3,3 м, ​ \( s \) ​ = 3,3 м 2) \( l \) = 3,3 м, \( s \) = 0,7 м 3) \( l \) = 0,7 м, \( s \) = 0,7 м 4) \( l \) = 0,7 м, \( s \) = 3,3 м

9. Решают две задачи. 1. Рассчитывают скорость движения поезда между двумя станциями. 2. Определяют силу трения, действующую на поезд. При решении какой задачи поезд можно считать материальной точкой?

1) только первой 2) только второй 3) и первой, и второй 4) ни первой, ни второй

10. Точка обода колеса при движении велосипеда описывает половину окружности радиуса ​ \( R \) ​. Чему равны при этом путь ​ \( l \) ​ и модуль перемещения ​ \( s \) ​ точки обода?

1) \( l=2R \) , ​ \( s=2R \) ​ 2) \( l=\pi R \) , \( s=2R \) 3) \( l=2R \) , \( s=\pi R \) 4) \( l=\pi R \) , \( s=\pi R \) .

11. Установите соответствие между элементами знаний в левом столбце и понятиями в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ЭЛЕМЕНТ ЗНАНИЙ A) физическая величина Б) единица величины B) измерительный прибор

ПОНЯТИЕ 1) траектория 2) путь 3) секундомер 4) километр 5) система отсчёта

12. Установите соответствие между величинами в левом столбце и характером величины в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами понятия правого столбца.

ВЕЛИЧИНА A) путь Б) перемещение B) проекция перемещения

ХАРАКТЕР ВЕЛИЧИНЫ 1) скалярная 2) векторная

Часть 2

13. Автомобиль свернул на дорогу, составляющую угол 30° с главной дорогой, и совершил по ней перемещение, модуль которого равен 20 м. Определите проекцию перемещения автомобиля на главную дорогу и на дорогу, перпендикулярную главной дороге.

Источник