Вращательное движение тела, формулы
|
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения. Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями. |
Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
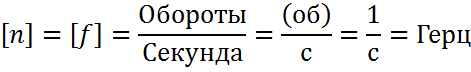
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если n — число оборотов, f — частота, T — продолжительность одного оборота, период, ? — угловое перемещение, N — полное число оборотов, t — время, продолжительность вращения, ? — угловая частота,
то
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.• вопреки своему названию число оборотов n — это не число, а физическая величина.• следует различать число оборотов n и полное число оборотов N
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- \( v=\Delta{s}/\Delta{t} \), где \( v \) — это скорость, \( \Delta{s} \) — перемещение, a \( \Delta{t} \) — время перемещения;
- \( a=\Delta{v}/\Delta{t} \), где \( a \) — это ускорение, \( \Delta{v} \) — изменение скорости, a \( \Delta{t} \) — время изменения скорости;
- \( \Delta{s}=v_0(t_1-t_0)+{}^1\!/\!_2a(t_1-t_0)^2 \), где \( v_0 \) — это начальная скорость, \( t_0 \) — это начальный момент времени, a \( t_1 \) — это конечный момент времени;
- \( v^2_1-v^2_0=2a\Delta{s} \), где \( v_1 \) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- \( \omega=\Delta{\theta}/\Delta{t} \), где \( \omega \) — угловая скорость, \( \Delta{\theta} \) — угол поворота, \( \Delta{t} \) — время поворота на угол \( \Delta{\theta} \);
- \( \alpha=\Delta{\omega}/\Delta{t} \), где \( \alpha \) — угловое ускорение, \( \Delta{\omega} \) — изменение угловой скорости, \( \Delta{t} \) — время изменения угловой скорости;
- \( \theta=\omega_0(t_1-t_0)+{}^1\!/\!_2a(t_1-t_0)^2 \), где \( \omega_0 \) — это начальная скорость;
- \( \omega^2_1-w^2_0=2as \), где \( \omega_1 \) — это конечная скорость.
Период и частота вращения
Важными характеристиками любого вращательного движения являются частота и период:
Определение
Период – время, за которое тело совершает полный оборот.
В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.
Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как \(2*\pi*R\), где \(R\) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость:
$$T=\frac{2*\pi*R}{V};$$
Подставив сюда формулу \((1)\) для линейной скорости через угловую:
$$T=\frac{2*\pi}{\omega};$$
Где \(V\) –линейная скорость вращения.
В системе СИ период измеряется в \(\).
Определение
Частота – количество оборотов за единицу времени.
В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.
Период и частота вращения связаны между собой выражением:
$$T=\frac{1}{\nu};$$
Отсюда можно получить формулы для частоты, подставив период:
$$\nu=\frac{V}{2*\pi*R}=\frac{\omega}{2*\pi};$$
Пример 1
Примеры решения задач
Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.
Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω — εt.
Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω/t = 2πn/t.
Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).
Угол поворота ротора центрифуги за время t будет: φ(t)= φ + ωt + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ = 0, находим: φ(t)= ωt/2 = πnt.
Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).
Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.
Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.
Найдем тормозной момент сил, действующий на диск: M = RF.
Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.
Найдем время, за которое диск остановится: t = ω/ε, где ω — начальная угловая скорость диска, которая равна 2πv.
Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).
Ответ: время остановки равно 2,5 с.
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если ? — угловое перемещение в радианах, s — длина дуги, заключенной
между сторонами угла поворота, r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ? от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость ? от t) и график углового ускорения (зависимость ? от t).
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость \( \omega \), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
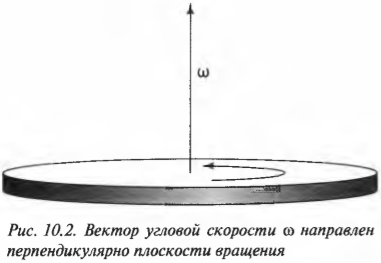
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где \( \alpha \) — угловое ускорение, \( \Delta\omega \) — изменение угловой скорости, \( \Delta t \)— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где \( \mathbf{\alpha} \) — вектор углового ускорения, а \( \Delta\mathbf{\omega} \) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.