Сюръекция, инъекция и биекция. обратное отображение. композиция отображений произведение множеств. график отображения

Какое точное определение инъективной функции

спросил
7 лет, 5 месяцев назад

Изменено
7 лет, 5 месяцев назад

Просмотрено
20 тысяч раз

$\begingroup$

Правильно ли я считаю, что функция инъективна, если некоторые элементы первого множества отображаются в некоторые элементы второго множества?

Возможно ли также, чтобы 4 элемента первого набора отображались на такой же элемент второго набора?

Это правильно?

Очень ценен простой ответ, уже достаточно запутанный

СПАСИБО

функции
определение

$\endgroup$

$\begingroup$

Интуиция подсказывает, что вы можете иметь копию $X$ в $Y$, это означает, что для всех $x\in X$ существует $y\in Y$, для которых $f(x)=y$ и не являются другими $x’$ с тем же утверждением, $\these$ Y содержит копию множества X

Примечание

$\endgroup$

$\begingroup$

Инъективная функция (она же функция взаимно однозначного вывода) — это функция, для которой каждый элемент диапазона функции соответствует ровно одному элементу области определения.

Это означает, что он никогда не сопоставляет различные элементы своего домена с одним и тем же элементом своего кодового домена.

$\endgroup$

$\begingroup$

Функция $f:X\rightarrow Y$ является не инъективной, если существуют два различных элемента $a,b\in X$ с $f(a)=f(b)$.

Если это не так, то функция инъективна.

$\endgroup$

$\begingroup$

Инъективная функция — это отношение, удовлетворяющее условию $f(x) = f(y) \Rightarrow x=y$.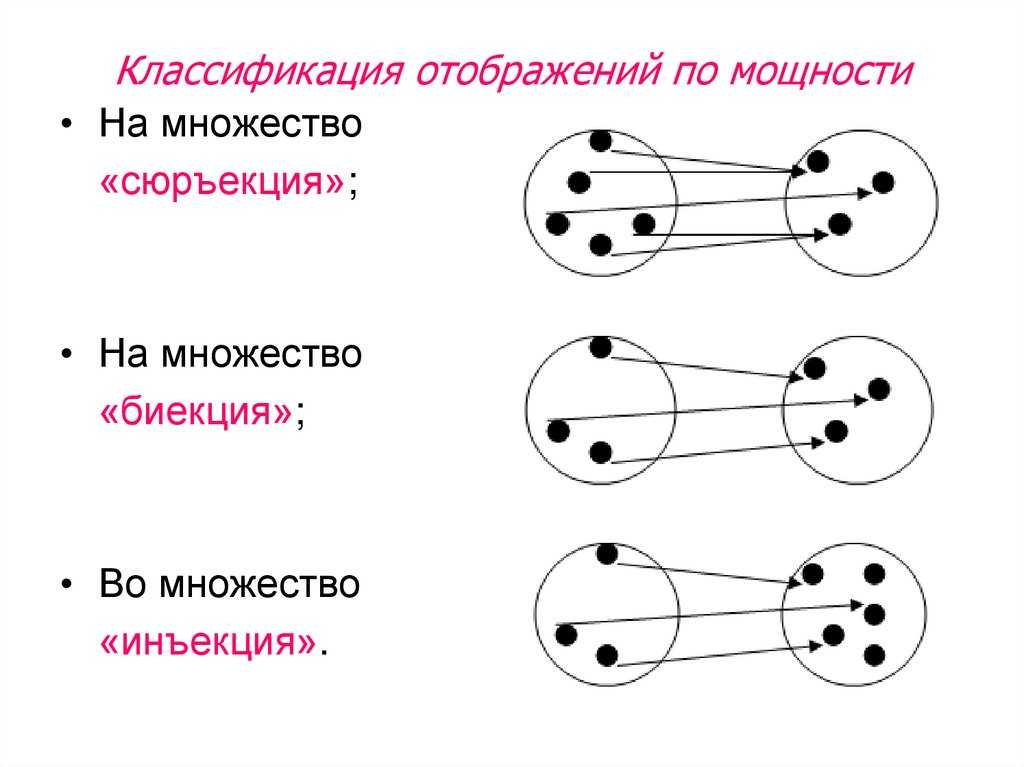

Другие свойства

Если г ∘ е инъективно, то е инъективна (но г не должно быть).
F : X → Y инъективен тогда и только тогда, учитывая любые функции г , ч : W → Х каждый разкогда е ∘ г = е ∘ ч , то г = ч . Другими словами, инъективными функции являются именно мономорфизмами в категорииНабор множеств.
Если F : X → Y инъективно и является подмножеством из X , то F -1 ( е ( )) = . Таким образом, может быть восстановлено из его образаF ( A ).
Если F : X → Y инъективно и и B оба являются подмножества X , то F ( ∩ B ) = F ( ) ∩ F ( B ) .
Каждая функция ч : W → Y можно разложить ч = е ∘ г для подходящего впрыска F и сюръекции г . Это разложение единственно с точностью до изоморфизма , и е можно рассматривать как функцию включения в диапазоне ч ( W ) в час , как подмножество области значений Y в час .
Если F : X → Y является инъективной функцией, то Y имеет по меньшей мере столько же элементы , как X , в смысле кардинальных чисел . В частности, если, кроме того, существует инъекция из Y F : X → Y инъективен тогда и только тогда , когда F является сюръективным (в этом случае е является взаимно однозначным ).
Инъективна функция , которая представляет собой гомоморфизм между двумя алгебраическими структурами является вложением .
В отличие от сюрьективности, который представляет собой отношение между графиком функции и ее области значений, приемистость является свойством графа только функции; то есть ли функция е инъективна может быть решен только с учетом графика (и не кообласть) от е .

Инъекции могут быть отменены

Функции с левой обратными всегда инъекции. То есть, учитывая п : X → Y , если существует функция г : Y → X , такие , что для любого х ∈ Х ,

то е инъективно. В этом случае, например , называется втягивание из F . С другой стороны , е называется раздел о г .

С другой стороны , каждая инъекция е с непустой областью имеет левый обратный г , которая может быть определена путем фиксации элемента а , в области F так , что г ( х ) равна уникальный прообраз х при е , если она существует , и г ( х ) = в противном случае.

Левый обратный г не обязательно является обратным из F , так как композиция в другом порядке, е ∘ г , может отличаться от идентичности на Y . Другими слова, инъективная функция может быть «отменена» по левым инверсиям, но не обязательно обратит , который требует , чтобы функция биективна .

Доказывая, что функции инъективны

Доказательство того, что функция е инъективно зависит от того, как представлена функция и какие свойства имеет функцию. Для функций, которые задаются по некоторой формуле есть основная идея. Мы используем контрапозицию из определения приемистости, а именно , что если е ( х ) = п ( у ) , то х = у .

Доказательство: Пусть F : X → Y . Пусть F ( х ) = F ( у ) . Таким образом , 2 х + 3 = 2 у + 3 ⇒ 2 х = 2 у ⇒ х = у . Поэтому, как следует из определения , что е инъективна.

Есть множество других способов доказать , что функция инъективна. Например, в исчислении , если F является дифференцируемой функцией , определенной на некотором интервале, то достаточно , чтобы показать , что производная всегда положительна или всегда отрицательна на этом интервале. В линейной алгебре, если F есть линейное преобразование, достаточно , чтобы показать , что ядро F содержит только нулевой вектор. Если е есть функция с конечной областью достаточно посмотреть список изображений каждого элемента домена и убедитесь , что изображение не происходит дважды в списке.

Функция f от A до B является назначением ровно одного элемента B каждому элементу A (A и B — непустые множества). A называется областью f, а B называется областью f. Если b является уникальным элементом B, назначенным функцией f элементу a из A, он записывается как f (a) = b. f отображает A в B. означает, что f является функцией от A до B, это записывается как

Термины, связанные с функциями:

Домен и совместный домен — если f является функцией из набора A в набор B, то A называется Доменом, а B называется совместным доменом.
Range — Range of f — множество всех изображений элементов A. В основном Range — это подмножество co-domain.
Изображение и предварительное изображение — b является изображением a, а a является предварительным изображением b, если f (a) = b.

Свойства функции:

Сложение и умножение: пусть f1 и f2 — две функции от A до B, тогда f1 + f2 и f1.f2 определены как: f1 + f2 (x) = f1 (x) + f2 (x). (Дополнение) f1f2 (x) = f1 (x) f2 (x). (Умножение)

Равенство: две функции равны только в том случае, если они имеют одинаковый домен, один и тот же домен и одни и те же элементы отображения из домена в один домен.

Типы функций:

Функция «один к одному» (Injective): функция вызывается один к одному, если для всех элементов a и b в A, если f (a) = f (b), то это должен быть случай, когда a = b. Он никогда не отображает отдельные элементы своей области в один и тот же элемент своей совместной области .

Мы можем выразить, что f один к одному, используя квантификаторы как или эквивалентно где вселенная дискурса является областью функции.

На функцию (сюръективную): если каждому элементу b в B соответствует элемент a в A, такой что f (a) = b. Не требуется, чтобы а был уникальным; Функция f может отображать один или несколько элементов A в один и тот же элемент B.

Функция соответствия один-к-одному (Bijective / Invertible): Функция — это Bijective-функция, если она является взаимно-однозначной и одной функцией.

Обратные функции: функция Bijection также известна как обратимая функция, потому что они имеют свойство обратной функции. Обратная биекция f обозначается как f -1 . Это функция, которая присваивает b уникальный элемент a такой, что f (a) = b. следовательно, f -1 (b) = a.

Некоторые полезные функции -:

Строго возрастающие и строго убывающие функции: функция f строго возрастает, если f (x)> f (y), когда x> y. Функция f строго убывает, если f (x) y. Функция f уменьшается, если f (x) ≤ f (y), когда x -1 of = f -1 (f (a)) = f -1 (b) = a.

fof -1 = f (f -1 (b)) = f (a) = b.
Если f и g оба являются функцией один к одному, то туман также является функцией один к одному.
Если f и g оба включены, то туман также включен.
Если f и туман оба являются однозначными функциями, то g также однозначно.
Если f и туман на, то не обязательно, что g также на.
(туман) -1 = г -1 из -1

Некоторые важные моменты:

Функция является однозначной, если она либо строго увеличивается, либо строго уменьшается.
Функция «один к одному» никогда не присваивает одно и то же значение двум различным элементам домена.
Для функции on диапазон и совмещенный домен равны.
Если функция f не является биективной, обратная функция от f не может быть определена.

Эта статья предоставлена Нитика Бансал

Отображения. Инъективные и сюръективные отображения

Если указан
закон, сопоставляющий каждому элементу
множества А единственный элемент
множества В, то говорят, что имеется
однозначное отображение
АВ.

Отображение
АВ
называется инъективным, если разные
элементы множестваA
переходят в разные элементы множества
B:
если а
в, то
.

Отображение
АВ
называется сюръективным, если каждый
элемент множества В имеет свой прообраз
в множестве А.

Если отображение
одновременно инъективное и сюръективное,
то оно называется биективным.

1.
Пусть f:
RR
задано формулой f(x)
= x2-1
(рис.3). Определить, является ли отображение
f
инъективным, сюръективным, биективным.

Область определения
функции – R,
область значений функции –
[-1;+).

f
– отображение.

Если (х,у) f и (х,z) f ,
то y
= z,
так как (x,y)f,
т.е. y
= x2-1,
(x,z)f,
т.е. z
= x2-1.
Найдутся х₁,
х₂R,
такие что
х₁х₂,
но: f(x₁)
= f(x₂),
например, пусть х₁= 1, х₂= -1, тогда
f(x₁)
= 0 и f(x₂)
= 0, т.е. х₁х₂,
а f(x₁)
= f(x₂).
Таким образом, это неинъективное
отображение.
Так как область
значений функции [1;+
)
не совпадает сR,
то отображение несюръективно.

2.
Пусть f:
RR
задано формулой f(x)
= x4.
Является ли отображение инъективным,
сюръективным?

Поскольку х₁=2R,
х₂=
-2R,
f(2)
= f(-2)
= 16, т.е. х₁х₂,
а f(x₁

)
= f(x₂),
то отображение неинъективно.
Для любого xR
не существует f(х),
такого что f(х)
= -16, так как х4-16, поэтому отображение несюръективно.

3.
Пусть отображение f:
[0;+)[0;+)
задано формулойf(x)=x2.
Является ли оно инъективным, сюръективным?

Для любых х₁,
х₂[0;+),
х₁х₂,
f(x₁)=x₁2,
f(x₂)=x₂2,
но f(x₁)
f(x₂),
т.е для каждого х существует единственное
f(x),
следовательно, f(х)
— инъективное отображение.
Для каждого
значения f(x)[0;+)
найдётся х[0;+),
поэтомуf(х)
— сюръективное отображение.

из
1. и 2. следует, что отображение биективно.

Всякое подмножество
Г декартова произведения АхА называется
отношением на множестве А.

Отношение Г
называют рефлексивным, если aГа
для всех aA.

Отношение Г
называют симметричным, если аГbbГа.

Отношение Г
называют транзитивным, если аГb,
bГааГс.

Если отношение
рефлексивно, симметрично, транзитивно,
то оно называется отношением
эквивалентности.

1.
Проверить, является ли D
отношением эквивалентности на R,
если D={(x;y)|
sin
x
= sin
y}.

D
– рефлексивно, так как для любого R
()D,
т.е. для любого x
R
имеем sin
x
= sin
x.
D
– симметрично, так как для любой пары
(,)D
имеем ()D,
т.е. для любых
R
из (x,y)D
следует, что sin
x
= sin
y,
тогда и sin
y
= sin
x,
следовательно, (y,x)D.
D
– транзитивно, так как для любых а,b,cR
из того что ()D
и ()D
следует, что ()D,
т. е. если (x,y)D,
то sinx=siny,
если (y,z)D,
то sin
y
= sin
z,
тогда sin
x=sin
z,
следовательно, (x,z)
D.