Нелинейные цепи постоянного тока

Методы расчета нелинейных цепей

Нелинейность параметров элементов усложняется расчетом цепи, поэтому рабочим участком выбирается или линейный, или близкий к нему участок характеристики. При этом рассматривается с допустимой точностью элемент как линейный. При невозможности этого применяются специальные методы расчета, такие, как:

• графический метод;
• метод аппроксимации.

Идея графического метода ориентирована на построение характеристик элементов цепи (вольт–амперной $u(i)$, вебер–амперной $ф(i)$ или кулон–вольтной $q(u)$) и их последующем графическом преобразовании с целью получения соответствующей характеристики для всей цепи или какого-то из ее участков.

Графический метод расчета считается наиболее простым и наглядным в использовании, обеспечивающим необходимую точность. В то же время, его применяют при незначительном количестве нелинейных элементов в цепи, поскольку он требует максимальной аккуратности при проведении графических построений.

Идея метода аппроксимации направлена на замену аналитическим выражением экспериментально полученной характеристики нелинейного элемента. Различают такие виды:

• аналитическая аппроксимация (при которой характеристика элемента заменяется на аналитическую функцию);
• кусочно–линейная (при ней характеристика элемента заменяется комплексом прямолинейных отрезков).

Точность аналитической аппроксимации определяет правильность выбора аппроксимирующей функции и подбор соответствующих коэффициентов. Преимуществом кусочно–линейной аппроксимации выступает простота при применении и возможность рассматривать элемент в формате линейного.

Более того, в ограниченном диапазоне изменений сигнала, где его, благодаря трансформациям, можно считать линейным (режим малого сигнала), нелинейный элемент (с допустимой точностью) можно заменить эквивалентным линейным активным двухполюсником:

$U = E + R_{диф} I$,

где $R_{диф}$ –дифференциальное сопротивление нелинейного элемента на линеаризуемом участке.

8.1. Нелинейные элементы

Основные радиотехнические преобразования осуществляются с помощью либо нелинейных цепей, либо линейных цепей с переменными параметрами. Однако последние реализуются тоже с помощью нелинейных элементов (например, емкость р-n-перехода в полупроводниковом диоде), а некоторые параметрические цепи сами работают в существенно нелинейном режиме (например, параметрический генератор). Поэтому можно считать, что свойства нелинейных элементов и цепей являются фундаментом для теории большинства реальных радиотехнических устройств. Приведем некоторые примеры нелинейных элементов.

Следует различать резистивные (сопротивления) и реактивные (индуктивности, емкости) нелинейные элементы.

Для радиотехнических цепей и устройств наиболее характерными и распространенными резистивными нелинейными элементами являются полупроводниковые, ламповые и любые другие приборы, используемые для усиления или преобразования сигналов и имеющие нелинейную вольт-амперную характеристику. Важным параметром резистивного нелинейного элемента является определенная соответствующим образом крутизна его характеристики.

Различают два следующих определения крутизны характеристики: а) в рассматриваемой рабочей точке при слабом сигнале (дифференциальная крутизна) и б) крутизна при сильном гармоническом колебании (средняя крутизна).

С первым определением крутизны, соответствующим линейному режиму работы прибора (рис. 8.1, а), мы имели дело в гл. 5, 6, где эта крутизна определялась выражением вида

где U приравнивалось U_{БЭ 0} (для транзистора).

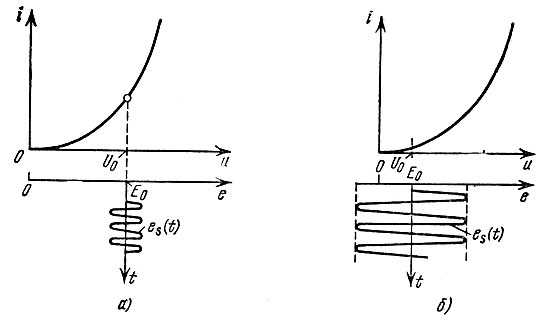Рис. 8.1. Линейный (а) и нелинейный (б) режимы работы элемента с нелинейной вольт-амперной характеристикой

Второе определение крутизны соответствует существенно нелинейному режиму работы устройства (рис. 8.1, б) и может быть дано лишь при учете формы вольт-амперной характеристики нелинейного элемента в пределах изменения входного воздействия (это будет сделано в § 8.4).

Примером нелинейной емкости может служить любое устройство, обладающее нелинейной вольт-кулонной характеристикой q(u). На рис. 8.2 изображены вольт-кулонная характеристика q_л(u) и вольт-фарадная характеристика С_л = q_л(u)/u = const для обычной линейной емкости и аналогичные характеристики q_нл и С_нл = q_нл(u)/u для нелинейной.

Рис. 8.2. Вольт-кулоная и вольт-фарадная характеристики линейного и нелинейного конденсатора

При любом характере зависимости C_нл для заряда q_нл, как и в случае линейной емкости, имеет место соотношение

В дальнейшем нелинейная емкость будет обозначаться С(u).

Если приложенное к емкости С(u) напряжение изменяется во времени, то ток через емкость можно определить с помощью одного из двух эквивалентных выражений:

Если напряжение u изменяется в небольших пределах в окрестности точки u = U, то емкость можно представить в виде

Определенную таким образом емкость иногда называют дифференциальной.

На рис. 8.3 изображен примерный вид зависимости С(u) для емкости полупроводникового диода.

Рис. 8.3. Примерный вид вольт-фарадной характеристики полупроводникового диода

Наконец, катушка с ферромагнитным сердечником, обтекаемая сильным током, доводящим сердечник до магнитного насыщения, является примером нелинейной индуктивности L(i).

Соотношение между током i и напряжением u на индуктивности следует из исходного выражения для потокосцепления

Очевидно,

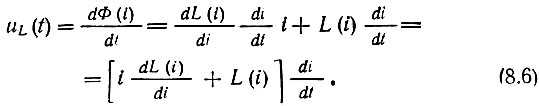
Если задано напряжение u_L(t) на индуктивности, то, очевидно,

и, как и в случае линейной индуктивности,

Под дифференциальной индуктивностью подразумевается величина

Понятиями дифференциальные сопротивление, емкость и индуктивность широко пользуются при рассмотрении воздействия относительно слабых сигналов на нелинейные элементы. При этом нелинейность элемента проявляется лишь в том, что величины R, С и L зависят от величины управляющего напряжения (или тока), определяющей положение рабочей точки на нелинейной характеристике. По отношению же к слабому сигналу подобный элемент является линейным устройством с переменным параметром (если управляющее напряжение изменяется во времени).

Свойства таких элементов рассматриваются в гл. 10.

Нелинейная электрическая цепь

Определение 2

Нелинейной электрической цепью считается та, которая содержит один или несколько нелинейных элементов.

Нелинейный элемент в электроцепи имеет параметры, зависимые от определяющих их величин. Нелинейная электрическая цепь имеет ряд важных отличий от линейной и в ней зачастую возникают специфические явления.

Нелинейные элементы характеризуют статические $R_{ст}$, $L_{ст}$, и $C_{ст}$ и дифференциальные $(R_д, L_д, C_д)$ параметры. Статические параметры нелинейного элемента определяются в виде отношения ординаты избранной точки характеристики к ее абсциссе:

$F_{ст} = \frac{yA}{YX}$

Дифференциальные параметры нелинейного элемента определяются в форме отношения малого приращения ординаты выбранной точки характеристики к малому приращению ее абсциссы:

$F{диф} = \frac{dy}{B}$

Нелинейные электрические цепи постоянного тока

Нелинейные свойства нелинейных цепей постоянного тока определяются наличием в них нелинейных резисторов. Так как в нелинейных резисторах отсутствует прямая пропорциональность между напряжением и током, они не могут быть охарактеризованы одним значением сопротивления. Соотношение между напряжением и током зависит от их мгновенных значений, а также интегралов и производных по времени. В зависимости от условий функционирования нелинейного резистора и характера поставленной задачи различают динамическое, статическое и дифференциальное сопротивления. В том случае, когда нелинейный элемент является безынерционным (характеристики не зависят от скорости изменения переменных), то он может быть охарактеризован статическим и дифференциальным сопротивлением, график которых изображен на рисунке ниже.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

В этом случае статическое сопротивление представляет собой отношение напряжения на резистивном элементе в протекающему через него электрическому току (точка 1 на рисунке), то есть:

$Rcm = U1 / I1 = mRtga$

Дифференциальное сопротивление является отношением бесконечно малого приращения напряжения к такому же приращению электрического тока, то есть:

$R = du / di = mRtgB$

У неуправляемого нелинейного резистора статическое сопротивление всегда больше нуля, значение дифференциального сопротивления может быть отрицательным.

1.2.1 Потери в сердечниках нелинейных индуктивных катушек, обусловленные вихревыми токами

Если по индуктивной катушке со стальным сердечником проходит
переменный ток, то в сердечнике возникает переменный магнитный поток, под
действием которого в листах сердечника образуются вихревые токи. В плоскости
листа, перпендикулярной магнитному потоку, по закону электромагнитной индукции
наводится ЭДС. Эта ЭДС вызывает в нем ток, который называют вихревым. Вихревые
токи по закону Ленца стремятся создать поток, встречный по отношению к
вызвавшему их потоку.

Потери энергии в листе на вихревые токи пропорциональны
квадрату наведенной в контурах листа ЭДС и обратно пропорциональны
сопротивлению контуров. ЭДС, наводимые в контурах, по которым замыкаются
вихревые токи, при заданной ширине листа пропорциональны толщине листа а,
амплитудному значению индукции и частоте. В свою очередь, сопротивление контура
пропорционально его периметру и удельному сопротивлению. Потери энергии на
вихревые токи пропорциональны квадрату амплитудного значения индукции, квадрату
частоты и квадрату толщины листа.

Уменьшить потери в листовом сердечнике на вихревые токи можно
двумя путями:

)        изготовлением сердечника из тонких изолированных
друг от друга листов

При частоте 50 Гц толщина листов обычно 0,35-0,5 мм; при
высоких частотах — до 0,005 мм.

Кроме потерь от вихревых токов в сердечнике есть еще потери,
обусловленные гистерезисом и магнитной вязкостью.

1.2.2 Потери в ферромагнитном сердечнике,
обусловленные гистерезисом

Ферромагнитным материалам свойственно явление гистерезиса,
которое вызвано отставанием изменения магнитной индукции от изменения
напряженности магнитного поля. Площадь гистерезисной петли в координатах,
снятая при достаточно медленном изменении магнитного поля во времени (когда
вихревые токи практически отсутствуют), характеризует энергию, выделяющуюся в
единице объема ферромагнитного материала за один период переменного тока (за
одно перемагничивание).

Потери в сердечнике, обусловленные гистерезисом,
пропорциональны объему сердечника, первой степени частоты и площади
гистерезисной петли. От толщины листов потери на гистерезис не зависят.

Гистерезисные петли при достаточно быстром изменении
магнитного поля во времени называют динамическими. Динамические петли шире
соответствующих статических за счет вихревых токов и магнитной вязкости.

Степень отличия динамической петли от соответствующей
статической зависит от скорости перемагничивания (от частоты), удельного
электрического сопротивления материал а, толщины листов, температуры и наличия
в магнитном потоке высших гармоник.

1.2.3 Схема замещения нелинейной индуктивной
катушки

В расчетном отношении нелинейную индуктивную катушку можно
представить в виде схемы на рисунке 6.

В ней параллельно с идеализированной (без потерь) нелинейной
индуктивностью включено сопротивление потери в котором имитируют потери энергии
в сердечнике на гистерезис и вихревые токи, а последовательно включено
резистивное сопротивление самой обмотки напряжение на нелинейной индуктивности.
Потери энергии на гистерезис и вихревые токи зависят от качества
ферромагнитного материала и толщины листов сердечника.

Рисунок
6. Схема замещения катушки

Если сердечник выполнен из низкокачественного магнитного
материала, то потери в нем относительно велики, а сопротивление достаточно мало
и ток может оказаться соизмеримым с током протекающим по идеализированной (без
потерь) нелинейной индуктивности; в этом случае ветвь с сопротивлением
необходимо учитывать в расчете.

Если же сердечник изготовлен из тонких листов высококачественного
магнитомягкого материала, то потери в сердечнике малы, а сопротивление очень
велико и потому ветвь с сопротивлением можно не учитывать. Часто вводят еще
одно упрощение: полагают резистивное сопротивление обмотки настолько малым, что
с падением напряжения в нем можно не считаться.

Переход от схемы замещения на рисунке 6, а, а к схеме замещения на
рис. 6, б, вызван стремлением облегчить расчет цепей. При этом учитывают
основной полезный нелинейный эффект (нелинейность между индукцией и
напряженностью и пренебрегают побочным вредным эффектом (потерями,
обусловленными гистерезисом и вихревыми токами в сердечнике).

Линейная электрическая цепь

Электрические цепи с постоянными параметрами считаются в физике такими цепями, в которых сопротивления резисторов $R$, индуктивность катушек $L$ и емкость конденсаторов $С$ будут постоянными и не зависимы от действующих в цепи напряжений, токов и напряжений (линейные элементы).

При условии независимости сопротивления резистора $R$ от тока, линейная зависимость между током и падением напряжения выражается на основании закона Ома, то есть:

$ur = R_хir$

Вольтамперная характеристика резистора при этом представляет собой прямую линию.

При независимости индуктивности катушки от величины тока, протекающего в ней, потокосцепление самоиндукции катушки $ф$ оказывается прямо пропорциональным этому току:

$ф = Lхil$

При условии независимости емкости конденсатора С от приложенного к обкладкам напряжения $uc$, накопленный на пластинах заряд $q$ и напряжение $uc$ оказываются связанными между собой через линейную зависимость.

При этом линейность сопротивления, индуктивности, а также емкости носит сугубо условный характер поскольку в действительности все реальные элементы электроцепи не линейны. При прохождении через резистор тока он будет нагреваться с изменением сопротивления.

При этом в нормальном рабочем режиме элементов подобные изменения обычно настолько несущественны, что при расчетах не берутся во внимание (такие элементы считаются в электрической цепи линейными). Транзисторы, функционирующие в режимах, когда применяются прямолинейные участки их вольтамперных характеристик, условно также могут рассматриваться в формате линейных устройств

Транзисторы, функционирующие в режимах, когда применяются прямолинейные участки их вольтамперных характеристик, условно также могут рассматриваться в формате линейных устройств.

Определение 1

Электрическая цепь, которая будет состоять из линейных элементов, называется линейной. Такие цепи характеризуют линейные уравнения для токов и напряжений и заменяются линейными схемами замещения.

НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

Элементы электрической цепи, параметры которых зависят от протекающего через них тока или напряжения на их зажимах, называются нелинейными, а цепи, содержащие хотя бы один нелинейный элемент, называются нелинейными цепями. Почти все реальные элементы электрических цепей обладают нелинейными свойствами в большей или меньшей степени, но наиболее распространенными элементами, используемыми в технике, являются элементы на основе полупроводниковых материалов. Диоды, транзисторы, варисторы, тиристоры и т.д. – Все эти элементы очень нелинейны. Например, характеристика варистора описывается уравнением / = ki a , где к и a – коэффициенты, зависящие от конструкции и материала элемента, т.е. варистор, как и все полупроводниковые элементы, упомянутые выше, является нелинейным резистором.

Процессы, происходящие в нелинейных цепях, описываются нелинейными дифференциальными уравнениями, и принцип суперпозиции не применим для расчета нелинейных цепей.

Из этого же графика видно, что при непрерывном увеличении напряжения источника U ток плавно увеличивается до , а затем скачком до , после чего продолжает плавно увеличиваться (участок 4-5).