Шаг 2: провести оси проекций
Оси проекций — это прямые, на которые происходит проецирование объекта. Прямые выбираются в зависимости от ориентации объекта в пространстве и от выбранной системы координат. Ось X обычно проводится горизонтально, а ось Y — вертикально. Ось Z выбирается таким образом, чтобы она была перпендикулярна оси X и оси Y.
Для того чтобы провести оси проекций, необходимо определить место расположения плоскости проекций и выбрать направление осей. В большинстве случаев выбирают такую систему координат, чтобы объект находился в положительном пространстве, то есть все координаты были положительными числами.
Если объект расположен ближе к одной из осей, то лучше выбрать ее в направлении объекта. Если же объект расположен под углом к осям проекций, то для простоты лучше выбрать такие координаты, чтобы ось, ближе всего соответствующая одной из осей объекта, была выбрана в направлении объекта, а другая ось — перпендикулярно ей.
После того, как выбраны направления осей проекций, их необходимо провести на поверхности объекта. Это можно сделать с помощью линейки и карандаша или на компьютере с помощью специальных программ, например, AutoCAD или SolidWorks.
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют , опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
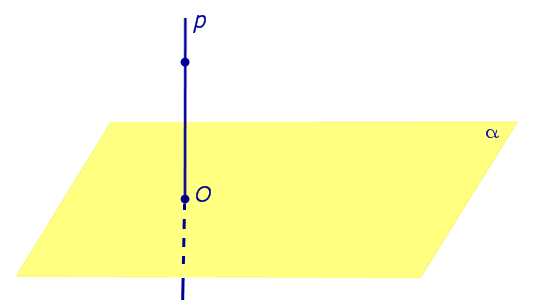
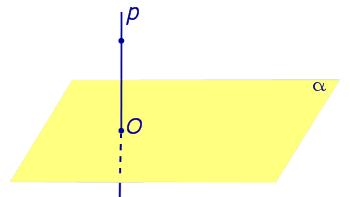
Рис.1
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия .
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся , называют наклонной к этой плоскости (рис. 2).
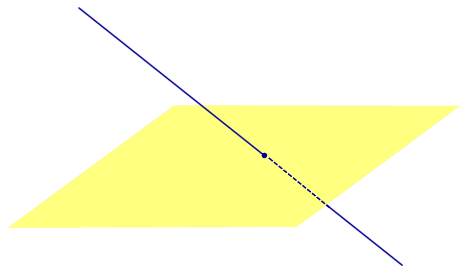
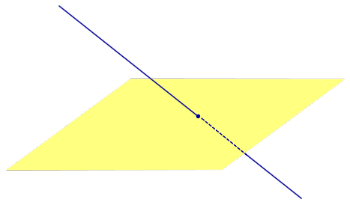
Рис.2
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
| Фигура | Рисунок | Свойство проекции |
|
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
||
|
На рисунке прямая PO, где P – любая точка прямой a, является α. Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a’, лежащая в плоскости α, a и проходящая через основание O перпендикуляра PO. |
||
|
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . |
||
| Прямая, перпендикулярная к плоскости |
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α. |
|
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α. |
|
На рисунке прямая PO, где P – любая точка прямой a, является α. Если прямая a параллельна плоскости α, то проекцией прямой a является прямая a’, лежащая в плоскости α, a и проходящая через основание O перпендикуляра PO. |
|
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a . |
| Прямая, перпендикулярная к плоскости |
|
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O, то точка O и является проекцией этой прямой на плоскость α. |
Пример ортогональной проекции круглого тела
Ортогональная проекция – это изображение объекта на плоскость, созданное перпендикулярным проецированием. Рассмотрим пример ортогональной проекции круглого тела.
Для начала выберем тело – круглую шаровую поверхность. Нам нужно получить его ортогональную проекцию на плоскость. Для этого выберем плоскость, на которую будем проецировать – пусть это будет плоскость xOy.
Далее, установим направление проекции – для ортогональной проекции это направление строго перпендикулярно плоскости, на которую проецируем. В нашем случае, это ось z.
Проекция на плоскость представляется в виде точек, каждая из которых – это проекция соответствующей точки шара. Чтобы получить ортогональную проекцию всего шара, нужно найти проекции его всех точек.
Полученные точки можно соединить прямыми линиями, чтобы получить контур проекции. Итоговое изображение будет выглядеть как круг с заданным радиусом.
Особенности ортогональной проекции в разных областях
Архитектура: В архитектурной графике ортогональная проекция позволяет создавать точные и четкие чертежи зданий, помещений и других конструкций. Она используется при разработке общего плана здания, деталей фасада и внутреннего устройства помещений. Однако в архитектурной графике могут применяться и другие виды проекций, такие как перспективная или аксонометрическая, чтобы лучше показать объем и форму объекта.
Инженерная графика: В инженерной графике ортогональная проекция часто используется для создания чертежей деталей машин, приборов, схем и других объектов. Она обеспечивает точность и ясность очертаний, а также позволяет получать различные виды проекций: первоначальную, вторичную, третичную и т.д. Благодаря этому инженеры могут лучше понимать размеры и форму объекта и создавать более качественные изделия.
Геометрическое моделирование: В компьютерной графике, в частности в 3D-моделировании, использование ортогональной проекции позволяет легко создавать и работать с геометрическими объектами. Ортогональная проекция используется для создания 2D-эскизов будущей модели и обеспечивает возможность создания текстурированной поверхности, которая даст более реалистичное представление о конечном продукте.
Математика: В математике ортогональная проекция используется для нахождения скалярного произведения векторов. Скалярное произведение может использоваться для нахождения проекции вектора на другой вектор или на плоскость. Этот тип проекции позволяет экспертам в области математики улучшать свои навыки решения проблем и применять их в других областях, таких как физика и инженерия.
Пример ортогональной проекции прямоугольного параллелепипеда
Ортогональная проекция — это проекция объекта на плоскость, перпендикулярную к прямой или плоскости, проходящей через объект. Для выполнения ортогональной проекции требуется знание геометрических принципов и техники точного рисования.
Примером ортогональной проекции может служить прямоугольный параллелепипед. Пусть стороны этого параллелепипеда равны a, b и c. Для выполнения ортогональной проекции на плоскость необходимо определить ее размеры и положение.
Размеры плоскости должны быть равны сторонам параллелепипеда, проходящим перпендикулярно к оси, которая должна быть параллельна поверхности нa которой проводится проекция, и должны быть отмечены на плоскости. Затем проводятся вертикальные линии из каждой точки на параллелепипеде вниз на плоскость. При проецировании изображения на плоскость использоваться все три параллельные оси (x, y и z). Результатом будет изображение параллелепипеда с отмеченными размерами и положением, которое соответствует его реальным пропорциям.
Ортогональная проекция является важным инструментом для инженеров, архитекторов, дизайнеров и других профессионалов в области конструирования. Она позволяет точно передать размеры и форму объектов на плоскости, что облегчает проектирование и изготовление различных конструкций.
Почему ортогональная проекция важна
Ортогональная проекция — это проекция объекта на плоскость, перпендикулярную к оси, проходящей через центр объекта. Она широко используется в проектировании, инженерии и архитектуре. Вот несколько причин, почему она важна:
Уменьшение сложности: Ортогональная проекция упрощает форму и размеры объекта, что упрощает проектирование и строительство. Это уменьшает сложность работы и позволяет сосредоточиться на главных аспектах проекта.
Точность: Ортогональная проекция позволяет более точно измерять и изображать различные детали и размеры объекта
Это важно для того, чтобы все элементы проекта соответствовали требуемым стандартам и были взаимозаменяемыми.
Понимание объекта: Ортогональная проекция дает лучшее представление о форме и отношениях между элементами объекта. С помощью этого можно лучше понимать, как объект функционирует и как лучше его использовать.
Снижение ошибок: Использование ортогональной проекции позволяет избежать ошибок в проектировании и строительстве объекта
Таким образом, можно сэкономить средства и время, устраняя потенциальные проблемы на более ранних стадиях разработки.
Улучшение проекта: Ортогональная проекция помогает лучше понимать проект и выявлять проблемы и несоответствия, что позволяет улучшить проект в целом. Это позволит создавать более эффективные проекты, которые соответствуют требованиям пользователей.
В целом, ортогональная проекция является очень важным инструментом для проектировщиков и инженеров. Она помогает упрощать процесс проектирования, улучшать проект и снижать возможность ошибок. Более того, она является ключевым элементом для создания более точных, эффективных и инновационных проектов в различных областях индустрии и архитектуры.
Ортогональная проекция в машиностроении
Ортогональная проекция является одним из основных методов графического изображения в машиностроении. Она используется для создания трехмерных моделей изделий и оборудования, которые затем могут быть реализованы на производстве.
При ортогональной проекции каждая точка объекта проецируется перпендикулярно на главные проекционные плоскости: горизонтальную, вертикальную и профильную. Это позволяет получить точные геометрические размеры деталей и обеспечить точность изготовления.
Для выполнения ортогональной проекции необходимы знания в области проекции, геометрии и математики. Кроме того, необходимы навыки работы с графическими компьютерными программами, такими как Autodesk AutoCAD, Solidworks и другие.
Ортогональная проекция позволяет создавать детальные чертежи для производства и конструирования, а также эффективно взаимодействовать с другими специалистами в области машиностроения.
Работа в машиностроении требует глубоких знаний и четкости в выполнении определенных задач. Ортогональная проекция является одним из наиболее важных элементов работы машиностроителей и помогает увеличивать производительность и уменьшать ошибки в производстве.
Шаг 3: выполнить проекцию
После того, как мы выбрали плоскость проекции и построили перпендикуляр к ней из точки, которую необходимо проецировать, мы можем приступить к выполнению самой проекции.
Ортогональная проекция может быть выполнена двумя способами: графическим и аналитическим. Графический способ заключается в нанесении точки на плоскость проекции и последующем проведении перпендикуляра из точки на эту плоскость. Точка пересечения перпендикуляра и плоскости становится проекцией исходной точки. Аналитический способ используется в случае, когда требуется получить координаты проекции точки на плоскость проекции. Он заключается в применении специальных формул.
Проекцию можно выполнить как в двумерном, так и в трехмерном пространстве. Для двумерного случая плоскость проекции выбирается параллельной одной из координатных плоскостей. В трехмерном пространстве плоскость проекции может быть любой плоскостью, проходящей через исходную точку и не являющейся параллельной осям координат.
Важно помнить, что ортогональная проекция сохраняет расстояния параллельных прямых. Это означает, что если мы проецируем на плоскость проекции две точки, которые находятся на параллельных прямых, то расстояние между ними на проекции будет таким же, как и на исходной прямой






























