Основные сведения об интерференции волн в физике

Математическое описание

Интерференция двух плоских волн

Пусть имеются две плоские волны: _>\cdot \exp^ t+_1 _1 + _1)>» width=»» height=»» /> и _>\cdot \exp^ t+_2 _2 + _2)>» width=»» height=»» />

Согласно принципу суперпозиции, результирующее поле при пересечении этих волн определяется суммой:

_2″ width=»» height=»» />

Интенсивность определяется соотношением:

_1 ^*_1+_1 ^*_2+_2 ^*_1 + _2 ^*_2″ width=»» height=»» />

Откуда с учетом: , I_2=E^2_» width=»» height=»» /> :

>_>\cdot \cos(_1_1-_2_2+_1 — _2)» width=»» height=»» />

Для простоты мы рассмотрим одномерный случай и выпрямление поляризованных волн, чтобы выражение для интенсивности можно было переписать в более простой форме:

E_>\cdot \cos(k_-k_)x+_1 — _2″ width=»» height=»» />

Интерференционная картина представляет собой чередование светлых и темных полос, шаг которых равен: -k_>» width=»» height=»» />

Примером такого случая является интерференционинтерференционная картина света, отраженного от поверхности плоскопараллельной пластины. свете.

Случай неравных частот

В некоторых учебниках и руководствах говорится, что что интерференция света возможно только для волн, генерируемых источником света с амплитудой или расстоянием между полями волновых фронтов. Это утверждение неверно. В смысле принципа суперпозиции. интерференция Она присутствует всегда, даже если волны от двух разных источников взаимодействуют. света. Правильнее было бы говорить о наблюдении или наблюдаемости. интерференционПоследнее не может быть постоянным. Последние не могут быть стабильными во времени, поэтому они размываются и исчезают. интерференционГраницы исчезнут. Рассмотрим две плоские волны с разными частотами:

_>\cdot \exp_t+_1 _1 + _1)>» width=»» height=»» /> и _>\cdot \exp_t+_2 _2 + _2)>» width=»» height=»» />

Согласно принципу суперпозиции, результирующее поле при пересечении этих волн определяется суммой:

_2″ width=»» height=»» />

Устройство, имеющее определенное характерное время записи (время экспозиции), делает изображение интерференционизображение. В физической оптике интенсивность — это усредненный по времени поток световочерез единицу площади, перпендикулярной направлению распространения волны. Время вычисления среднего значения определяется временем интеграции фотодетектора, а для устройств, работающих в режиме накопления сигнала (камеры, фотопленка и т.д.), — временем экспозиции. Поэтому приемники оптического излучения реагируют на среднее значение тока энергии. То есть, сигнал фотодетектора пропорционален

>^2>_\tau» width=»» height=»» />

где означает среднее значение. Во многих научных и технических приложениях эта концепция обобщается на все волны, включая непланарные. Поскольку в большинстве случаев, например, в соединенных с интерференцией и дифракцией света, В задачах, где речь идет в основном о пространственном положении максимумов и минимумов и их относительной интенсивности, постоянными множителями, не зависящими от пространственных координат, часто пренебрегают. По этой причине его часто рассматривают:

Интерференционная пила в узорах, сформированных на дорогах

Мы часто видели полноцветные узоры на дороге в сезон дождей. Это пример вмешательства.

Из-за разбросанного по дороге какого-нибудь маслянистого вещества или, скажем, разлива нефти в океане или море, на ней плавает маслянистый слой, вызывая помехи. Как когда белый свет падает на них, они отражают. Отражение происходит как от верхней поверхности, так и от внутреннего слоя. Когда световой луч падает, он претерпевает интерференцию в основном из-за маслянистого слоя.

Помехи на дороге из-за маслянистого материала Изображение Фото: «Дождь на масле на дороге» by микког под лицензией CC BY 2.0

Из-за наличия маслянистого слоя на дорогах или море при попадании света претерпевают конструктивное вмешательство и деструктивное вмешательство. Некоторые цвета света, проходящие через конструктивную интерференцию, вызывают видимый световой узор, тогда как цвета света при деструктивной интерференции не видны.

Помехи в антибликовом покрытии

В нашей повседневной жизни мы обычно используем спецификации. Мы очень часто находим цвета видимыми, когда свет падает на нашу линзу в спецификациях. Это происходит из-за помех.

Помехи в отражающем покрытии камеры Изображение Фото: «Объективы Contax Carl Zeiss на Canon 5D» by Уилсон Хуэй под лицензией CC BY-SA 2.0

Ведь все подобные аппараты имеют на своей поверхности световозвращающее покрытие. Однако отражающее покрытие на линзах, камере и т. д. предназначено для уменьшения интенсивности падающего на нее света. Формирование цветового рисунка на таком аппарате происходит за счет конструктивной интерференции света на верхней и нижней поверхностях.

Нестационарная интерференция света

К ней от­но­сят­ся све­то­вые бие­ния, на­блю­даю­щие­ся при на­ло­же­нии све­то­вых по­лей разл. час­тот. В этом слу­чае воз­ни­ка­ет бе­гу­щая в про­стран­ст­ве ин­тер­фе­рен­ци­он­ная кар­ти­на, так что в за­дан­ной точ­ке про­стран­ст­ва ин­тен­сив­ность све­та пе­рио­ди­че­ски ме­ня­ет­ся во вре­ме­ни с час­то­той, рав­ной раз­но­сти час­тот ин­тер­фе­ри­рую­щих волн. Бие­ния воз­ни­ка­ют в обыч­ных (не­ла­зер­ных) схе­мах И. с. при из­ме­не­нии во вре­ме­ни раз­но­сти хо­да ин­тер­фе­ри­рую­щих лу­чей. При­ме­ром мо­жет слу­жить ин­тер­фе­ро­метр Май­кель­со­на с пе­ре­мен­ной дли­ной од­но­го из плеч. При пе­ре­ме­ще­нии вдоль лу­ча све­та од­но­го из зер­кал ин­тен­сив­ность све­та на вы­хо­де ин­тер­фе­ро­мет­ра пе­рио­ди­че­ски ме­ня­ет­ся, что мо­жет слу­жить сред­ст­вом из­ме­ре­ния ско­ро­сти очень мед­лен­ных пе­ре­ме­ще­ний. Напр., при дви­же­нии зер­ка­ла со ско­ро­стью 10–6 м/с ин­тен­сив­ность све­та ме­ня­ет­ся с час­то­той ок. 4 Гц.

Бие­ния мо­гут на­блю­дать­ся и в из­лу­че­нии не­за­ви­си­мых ис­точ­ни­ков све­та. Для это­го их яр­ко­сти и спек­траль­ные плот­но­сти из­лу­че­ния долж­ны быть очень ве­ли­ки. Обе эти ха­рак­те­ри­сти­ки вы­ра­жа­ют­ся че­рез па­ра­метр вы­ро­ж­де­ния фо­то­нов $ρ$, рав­ный чис­лу фо­то­нов в объ­ё­ме ко­ге­рент­но­сти. При фо­то­элек­трич. ре­ги­ст­ра­ции бие­ний па­ра­метр $ρ$ в про­из­ве­де­нии с кван­то­вым вы­хо­дом при­ём­ни­ка оп­ре­де­ля­ет ве­ли­чи­ну сиг­на­ла бие­ний по от­но­ше­нию к фо­ну фо­тон­но­го шу­ма. Из­лу­че­ние ла­зе­ров силь­но вы­ро­ж­де­но $(ρ≫1)$, вслед­ст­вие че­го бие­ния в све­те двух ла­зе­ров и ме­ж­ду разл. ти­па­ми ко­ле­ба­ний од­но­го ла­зе­ра лег­ко на­блю­да­ют­ся. Эти бие­ния час­то иг­ра­ют вред­ную роль как ис­точ­ник мощ­но­го шу­ма ла­зе­ра.

Для те­п­ло­вых ис­точ­ни­ков обыч­но $ρ≪1$, по­это­му эф­фек­ты не­ста­цио­нар­ной И. с. в их из­лу­че­нии край­не ма­лы. Тем не ме­нее их уда­лось об­на­ру­жить в тон­ких экс­пе­ри­мен­тах по кор­ре­ля­ции ин­тен­сив­но­стей.

И. с. ис­поль­зу­ет­ся при спек­траль­ном ана­ли­зе све­та, для точ­но­го из­ме­ре­ния рас­стоя­ний, уг­лов, ско­ро­стей, в реф­рак­то­мет­рии. Боль­шое зна­че­ние ин­тер­фе­ро­мет­рия име­ет в оп­тич. про­из­вод­ст­ве как сред­ст­во кон­тро­ля ка­че­ст­ва по­верх­но­стей и лин­зо­вых сис­тем. Ин­тер­фе­рен­ци­он­ные яв­ле­ния ис­поль­зу­ют­ся для соз­дания све­то­фильт­ров, вы­со­ко­ка­че­ст­вен­ных зер­кал, про­свет­ляю­щих по­кры­тий для оп­тич. де­та­лей. И. с. со­став­ля­ет ос­но­ву оп­тич. го­ло­гра­фии.

Интерференция и дифракция

Интерференция — это изменение средней плотности потока энергии, вызванное суперпозицией волн.

Или немного по-другому: Интерполяция — это пространственное сложение волн, приводящее к временному постоянному распределению амплитуды суммарных колебаний.

Интерференцией волн света это комбинация волн, в которой существует временная постоянная картина усиления или ослабления суммарных колебаний света в различных пространственных точках. Термин интерференция в науку ввел Т. Юнг.

Условия возникновения интерференции

Для того чтобы суперпозиция волн имела постоянную интерференционДля получения стабильного изображения источники волн должны иметь одинаковую частоту и постоянную разность фаз. Такие источники называются когерентными. Когерентные волны — это волны, генерируемые когерентными источниками.

Поэтому только суперпозиция когерентных волн приводит к стабильному интерференционная картина.

В оптике для того, чтобы создать интерференционкогерентная схема, генерируются когерентные волны:

1. делением амплитуды волны;
2. делением фронта волны.

Условие минимумов интерференции

Амплитуда колебаний интерферирующих волн в рассматриваемой точке минимальна, если разность путей ( ) волн в этой точке содержит нечетное число полуволн ( ):

_0,\left(m=0,1,\dots \right) \qquad (2) \» width=»265″ height=»18″ />

Проблема когерентности волн

Для возникновения интерференционных полос недостаточно двух источников света, излучающих с одинаковой частотой. В повседневной жизни можно видеть множество примеров, когда при наличии таких источников (например, светящихся одноцветных светодиодов в гирлянде) никаких светлых и темных полос не возникает.

В реальности световые волны, за исключением тех, что излучают некоторые лазеры, не совпадают по частоте с достаточной для появления интерференционной картины точностью. Источник света состоит из атомов, излучающих свет независимо друг от друга в хаотической последовательности и с интервалами порядка $\tau = 10^{–8}$ с.

Это можно объяснить следующим образом. Результирующие волны от очень большого числа источников существует в течение очень краткого периода времени, после чего в процесс вступает другая группа излучающих атомов. Суммарное излучение меняет амплитуду и фазу, т.е. интерференционная картина появляется на чрезвычайно малые моменты времени, неразличимые с помощью оптических приборов. Фрагменты испускаемого света продолжительностью $\tau$ называют цугами. Их длина в пространстве равна $c \cdot τ$, где $c$ – скорость света. Фазы разных цугов не совпадают, поэтому мы видим не интерференционную картину, а хаотический по фазе набор цугов, т.е. эти колебания некогерентны, а интерференционные полосы хаотически перемещаются и глаз или фотоприбор вместо них видит лишь точки с усредненной освещенностью.

Интерференция света в тонких пленках

Картину интерференции часто можно наблюдать в тонких пленках, например, таких, какие образуются на поверхности воды при попадании на нее маслянистых прозрачных жидкостей. Такие вещества, будучи легче воды, растекаются по ее поверхности до тех пор, пока их толщина не будет представлять собой всего несколько слоев молекул. Это расстояние сопоставимо с длиной световой волны. К тому же наружная и внутренняя поверхности таких пленок параллельны с высокой точностью.

Интерференционная картина при попадании света на такую пленку получается потому, что часть пучка отражается от внешней ее стороны, а часть, пройдя сквозь пленку, отражается от внутренней.

Поскольку оптическая плотность пленки отличается от оптической плотности среды, из которой пришел световой пучок, световой луч преломляется при вхождении в пленку и выходе из нее. От точки, где такой луч выходит из пленки, может отразиться еше один луч, пришедший из того же источника. Таким образом, для наблюдателя эта точка будет выглядеть как источник двух независимых лучей, светящих с одной частотой, но с разностью по фазе, возникающей в результате задержки при прохождении первого луча сквозь пленку. Эта разность зависит от угла, под которым наблюдатель смотрит на точку, а математические закономерности, описывающие характеристики результирующей волны, будут такими же, как в опыте Юнга.

Особенностью интерференционной картины, порождаемой тонкими пленками, является то, что на них меняется не интенсивность освещения, а цвета, которые при изменении угла зрения «переливаются», создают радужные картины. Это связано с тем, что длина волны результирующего пучка настолько мала, что сопоставима с длинами волн различных цветов. Если пленка немного утончается (например, вследствие ветра, колышущего поверхность воды), цвет интерференционной картины смещается к синей стороне спектра, если утолщается — к красной.

Зависимость длины результирующей волны от толщины пленки можно описать формулой

$2dn = m \cdot \lambda$ ,

где $d$ — толщина пленки, $n$ — коэффициент, отражающий оптическую плотность вещества пленки и, следовательно, обуславливающий коэффициент преломления.

Интерференция в тонких пленках

Тем не менее интеференцию света удается наблюдать. Хотя ее и наблюдали очень давно, но только не придавали этому значения.

Вы тоже много раз видели интерференционную картину, когда в детстве развлекались пусканием мыльных пузырей или наблюдали за радужным переливом цветов такой пленки керосина либо нефти на поверхности воды. «Мыльный пузырь, витая в воздухе… зажигается всеми оттенками цветов, присущими окружающим предметам. Мыльный пузырь, пожалуй, самое изысканное чудо природы» (Марк Твен). Именно интерференция света делает мыльный пузырь столь достойным восхищения.

Английский ученый Томас Юнг первым пришел к гениальной мысли о возможности объяснения цветов тонких пленок сложением волн 1 и 2 (рис. 8.48), одна на которых (1) отражается от наружной поверхности пленки, а другая (2) — от внутренней. При этом происходит интеференция световых волн — сложение двух волн, вследствии которого наблюдается устойчивая во времени картина усиления или ослабления результирующих световых колебаний в различных точках пространства. Результат интерференции (усиление или ослабление результирующих колебаний) зависит от угла падения света на пленку, ее толщины и длины волны света. Усиление света произойдет в том случае, если преломленная волна 2 отстанет от отраженной волны 1 на целое число длин волн. Если же вторая волна отстанет от первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света.1 Исключение составляют квантовые источники света, лазеры, созданные в 1960 г. Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, возникает из-за того, что они являются частями одного и того же светового пучка. Цуг волн от каждого излучающего атома разделяется пленкой на два цуга, а затем эти части сводятся вместе и интерферируют.

Юнг понял также, что различие в цвете связано с различием в длине волны (или частоте световых волн). Световым пучкам различного цвета соответствуют волны с разной длиной волны . Для взаимного усиления волн, отличающихся друг от друга длиной волны (углы падения предполагаются одинаковыми), требуется различная толщина пленки. Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом должны появиться различные цвета.

Интерференция света

В обычной жизни наблюдать интерференцию света от двух источников невозможно. Происходит это потому, что обычные источники света некогерентны: у них, как правило, неодинакова частота, и фаза излучения меняется со временем.

Однако, если две световых волны будут являться частями одного светового пучка, можно добиться, чтобы возникла интерференционная картина.

Наиболее частым примером интерференции света, доказывающим волновую его природу, является появление радуги на тонкой поверхности мыльного пузыря или масла на воде. Луч света, попавший в тонкую пленку, отражается от двух ее поверхностей, образуя внутри пленки два когерентных луча. При сложении эти лучи образуют чередование светлых и темных полос. При этом еще играет роль и разность толщины пленки: условия чередования в разных местах выполняются для света разной длины. В результате на тонкой пленке суммарная интерференционная картина складывается из интерференционных картин разных длин волн, образуя радужные переливы.

Рис. 3. Радужные переливы на воздушных пузырях.

Что мы узнали?

Интерференция — это явление сложения двух волн, в результате которого в среде появляются участки волны с двойной и с нулевой амплитудой. Условия максимумов и минимумов описываются специальными формулами. Появление интерференционной картины на тонких пленках доказывает волновую природу света.

1. /10

   Вопрос 1 из 10

Условия максимумов и минимумов

Вкратце, схема образования интерференционной картины следующая. В момент встречи двух волн одинаковой амплитуды их сложение дает некоторое значение амплитуды: от нуля до двойной амплитуды.

Для того чтобы в данной точке суммарная волна колебалась с удвоенной амплитудой, необходимо, чтобы разность фаз в этой точке была равна нулю, а это возможно, если в разность хода волн $Δd$ укладывается целое число волн (четное число полуволн):

$$Δd_{max} = \pm k\lambda$$

Для того чтобы суммарная волна имела нулевую амплитуду, необходимо, чтобы фаза одной волны отличалась от другой на половину периода. То есть в разность хода должно укладываться нечетное число полуволн:

$$Δd_{min} = \pm (2k+1){\lambda \over 2}$$

Если разность хода имеет величину, в которую не укладывается целое число полуволн, то результирующая амплитуда будет иметь некоторое промежуточное значение.

Рис. 2. Условия максимума и минимума интерференции.

Помехи в лампах накаливания

Для возникновения интерференции необходимы два условия. Во-первых, два используемых источника света должны быть когерентными, а это значит, что две световые волны должны иметь между собой постоянную фазу. Во-вторых, световые волны должны иметь одну длину волны и, наконец, должен подразумеваться принцип наложения.

Теперь для того, чтобы в лампочке накаливания возникли помехи, должны быть облегчены все упомянутые выше условия. Но, как мы знаем, две одинаковые лампочки не могут производить световые волны с одинаковой фазой или частотой. Лампа производит световые волны, которые не являются когерентными. Это говорит нам о том, что испускаемые фотоны света имеют частоту, случайно связанную с любыми другими фотонами, испускаемыми той же лампочкой. 

Интерференция световой волны лампочками Изображение Фото: «Лампы накаливания» Гамма-Рей Продакшнс  CC BY 2.0

Следовательно, для возникновения интерференции в лампе накаливания источник двух световых волн должен быть одним и тем же. Два фотона световых волн имеют одну пару фотонов, чтобы вызвать интерференцию. 

Однако только два идентичных лазера с высоко стабилизированными частотами могут создавать видимую интерференционную картину на поверхностях.

Интерференция в тонких плёнках

Если вы смотрите на переливающийся разными цветами мыльный пузырь, на радужные отблески масляных или бензиновых пятен на поверхности воды, вы не воспринимаете ничего другого, как интерференцию света!

Давайте посмотрим на рис. 3 На поверхность тонкой прозрачной пленки падает световой луч .

Рис. 3. Интерференция на тонкой пленке

Падающий луч разделяется на два луча: отраженный и преломленный. После вторичного отражения и преломления второй луч выходит из пленки параллельно отраженному лучу.

Оба луча фокусируются в точку с помощью фокусирующей линзы. Это, пожалуй, самая распространенная линза (при наблюдении интерференционПервый луч фокусируется оптической системой нормального глаза (при прямом наблюдении).

Две волны и, которые являются частью одной волны, являются когерентными. В действительности, две копии цуга сходятся в одной точке с постоянным сдвигом фаз между ними; этот сдвиг обеспечивается разницей в пути между волнами и. Поэтому волны взаимодействуют друг с другом и создают в окружающем пространстве изображение чередующихся максимумов и минимумов.

Предположим, что пленка освещается белым светом. светом. Как вы знаете, белые свет представляет собой смесь волн с различными частотами; эти частоты соответствуют цветам от красного до фиолетового. Например, предположим, что разница в длине волны между и равна интегральному числу длин волн красного цвета света. Тогда красная составляющая белого света будет усилен, и свет, отраженный от пленки свет будет казаться нам красным.

Небольшое изменение угла падения (или толщины пленки) также изменит разность путей. Таким образом, если поверхность пленки неровная (или если мы смотрим с немного другого направления), то новая разность путей может соответствовать целому ряду длин волн, например, зеленому цвету света. Теперь зеленый компонент белого цвета усиливается. света, и отражается от фильма. свет мы увидим зелёным.

Все это мы можем наблюдать, глядя на мыльный пузырь. Смещение поверхности приводит к постоянному изменению разности при определенном укорочении. Усиливается один цвет, затем другой, и в результате получается пузырь, который светится всеми цветами радуги.

Физика 9 кл. Интерференция света. Опыт Юнга

Подробности

Обновлено 18.06.2019 17:19

Просмотров: 400

1. Какие два взгляда на природу света существовали с давних пор среди ученых?

С давних пор существовало два взгляда на природу света — две теории: корпускулярная и волновая.
Одни ученые считали, что свет — это поток частиц (корпускул).
Другие рассматривали свет, как волну.
До начала XIX в. не было доказательств ни в пользу волновых, ни в пользу корпускулярных представлений.
В 1802 г. английский ученый Томас Юнг на опыте показал, что свету присуще свойство интерференции, значит, свет — это волны.
К концу 19 в. в ходе экспериментов стало ясно, что некоторые явления можно объяснить только на основе корпускулярных представлений о свете, т. е. рассматривая его как поток частиц.
В настоящее время признана справедливой как волновая, так и корпускулярная теория.
Обе теории, дополняя друг друга, позволяют объяснять многие физические явления.

2. В чем заключалась суть опыта Юнга, что этот опыт доказывал и когда был поставлен?

В 1802 г. английский ученый Томас Юнг поставил опыт по сложению пучков света от двух источников, в результате чего получил не меняющуюся во времени картину, состоящую из чередующихся светлых и темных полос.
Юнг правильно объяснил возникновение полос интерференцией света.

Однако интерференция присуща только волновым (т. е. периодическим) процессам.
Поэтому oпыт Юнга стал доказательством того, что свет обладает волновыми свойствами.

3. В чем заключается интерференция звуковых волн?

При наложении двух когерентных волн (т. е. волн с одинаковой частотой и постоянной разностью фаз) образуется так называемая интерференционная картина, т. е. не меняющаяся со временем картина распределения амплитуд колебаний в пространстве.

В одних точках пространства колебания всегда происходят с максимальной амплитудой.
Это те точки, в которые колебания от обоих источников в любой момент времени приходят в одинаковых фазах и поэтому всегда усиливают друг друга.
В других точках колебания происходят с минимальной амплитудой.
Эти точки расположены по отношению к источникам так, что к ним колебания всегда приходят в противоположных фазах, ослабляя друг друга (а при равных амплитудах колебаний волны в любой момент времени полностью гасят друг друга).
В остальных точках колебания также происходят с постоянными амплитудами, значения которых лежат в промежутке от минимальной до максимальной.

4. Как на опыте можно получить интерференционную картину света?

На проволочное кольцо с ручкой, затянутое мыльной пленкой, в затемненном помещении направляется свет желтого цвета.
На пленке образуются горизонтально расположенные чередующиеся желтые и черные полосы.

5. Как объяснить появление на мыльной пленке чередующихся полос?

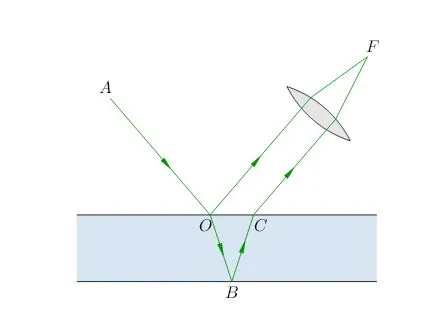
Свет, падая на пленку, частично отражается от передней поверхности в точке А, а частично проходит внутрь пленки и отражается от задней поверхности в точке В, после чего выходит из пленки в точке С.
Волны, выходящие из точек A и C, являются когерентными, т,к. они образуются от одного и того же источника.
Разность хода длин волн зависит от толщины пленки, которая в разных точках различна.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С, имея одинаковые фазы, то эти волны при сложении усилят друг друга.
В результате возникнет максимум интерференционной картины — желтая полоса.
Если толщина пленки окажется такой, что волны будут выходить из точек А и С в противоположных фазах, то эти волны при сложении будут гасить друг друга.
В результате возникнет минимум интерференционной картины — темная полоса.

6. Что доказывает опыт с освещением мыльной пленки?

Этот опыт доказывает, что раз наблюдается явление интерференции, значит, свет обладает волновыми свойствами.

7. Что можно сказать о частоте (или длине волны) световых волн разных цветов?

Томас Юнг измерил еще и длину световой волны.
Оказалось, что свету разных цветов соответствуют волны разной длины (разной частоты).
Например, красному свету в световом диапазоне соответствует самая большая длина волны ( иначе самая маленькая частота).
Длины волн убывают (а частоты возрастают) в следующей последовательности цветов: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.

Следующая страница — смотреть

Назад в «Оглавление» — смотреть

Интерференция механических волн

Для лучшего понимания этого явления интерференции, Давайте сначала объясним это на примере механических волн, которые легче наблюдать. Часто бывает так, что в среде одновременно распространяются несколько различных волн. Например, когда в помещении одновременно присутствуют несколько источников звука. Что же происходит, когда волны пересекают друг друга? Поясним это на примере волн, образующихся на поверхности воды.

Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, то можно увидеть, что каждая волна проходит через другую. И она ведет себя так, как будто другой волны никогда не существовало. Именно так В воздухе может одновременно распространяться любое количество звуковых волн. И они не будут влиять друг на друга. Количество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые мы воспринимаем одновременно. Звуки не превращаются в шум: Наши слуховые аппараты легко различают отдельные звуки.

Теперь давайте более подробно рассмотрим процесс наложения волн. Для этого мы будем наблюдать за рябью на поверхности воды, исходящей от двух камней, брошенных в воду. Таким образом, мы увидим, что некоторые участки поверхности остаются ненарушенными, в то время как на других участках нарушенность увеличилась. Если два пика двух волн встречаются в одной точке, то возмущение поверхности воды в этой точке становится сильнее. Если гребень одной волны встречается со впадиной другой, поверхность воды в этой точке остается спокойной. Видно, что в любой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы в среде является алгебраической суммой смещений, которые произошли бы, если бы одна из волн распространялась в отсутствие другой.

Интерференция — это сумма волн в пространстве, которая производит постоянное во времени распределение амплитуд результирующих колебаний частиц в среде.

Чтобы определить условия, при которых человек наблюдает интерференция Возбудим две круговые волны в ванне с помощью двух сфер, прикрепленных к стержням и вибрирующих по гармоническому закону.

Теперь давайте воспроизведем это явление интерференции схематично. В любой точке M на поверхности воды колебания вызываются двумя волнами от источников O₁ и О₂ (Амплитуды колебаний, создаваемых двумя волнами в любой точке M, различны, если волны движутся по разным путям d₁ и г₂. Однако, если расстояние l между источниками намного меньше этих путей, можно считать, что две амплитуды приблизительно равны.

Результат сложения волн, приходящих в точку М, зависит от разности фаз между ними. Проходя различные расстояния d₁ и г₂ волны имеют разность путей, определяемую формулой:

Если разность путей равна длине волны λ, то вторая волна отстает от первой на один период. Поскольку волна проходит расстояние, равное ее длине волны, за один период, их фазы совпадают в точке, где две волны встречаются. Если в этой точке волны имеют пики, то пики совпадают; если впадины, то впадины совпадают.