Проницаемость

Типы проницаемости

По типам
проницаемости можно определять:

• Абсолютную
• Эффективную (фазовую)
• Относительную

Абсолютная проницаемость

Абсолютная проницаемость горной породы – это проницаемость, измеренная при фильтрации одной фазы (флюида) через исследуемый образец. Причем данная фаза должна быть инертна к пористой среде. Данный тип проницаемости является характеристикой физических свойств самой породы и зависит от размера и структуры поровых каналов.

Как правило,
данный тип проницаемости определяется по при фильтрации газа (азота) через
образец породы с вводом поправок Клинкенберга, а эксперимент проводится на
полностью проэкстрагированном и очищенном образце.

Важно понимать, что в реальности пласты коллекторы содержат не только нефть и газ, но также некоторое количество остаточной воды, которая всегда присутствует в породах коллекторах до начала миграции в них нефти из нефтематеринских пород. При движении
нескольких не смешивающихся между собой флюидов, проницаемость для каждого из
флюидов будет меньше значения абсолютной проницаемости

При движении
нескольких не смешивающихся между собой флюидов, проницаемость для каждого из
флюидов будет меньше значения абсолютной проницаемости.

Фазовая (эффективная) проницаемость

Фазовая (эффективная) проницаемость – проницаемость образца для отдельно взятого флюида при наличии в ней как минимум одного другого флюида (фазы). Она зависит от насыщения породы тем или иным флюидом (количественного содержания флюида), а также от физико-химических свойств этих флюидов и возникающих капиллярных сил.

Относительная фазовая проницаемость

Относительная фазовая проницаемость (ОФП) – отношение эффективной проницаемости к абсолютной для того же образца.

Формула расчета относительной проницаемости

Понятие ОФП было введено для нормализации значений фазовой проницаемости по значению абсолютной проницаемости для того же образца.

Немаловажный момент – как при малых так и при больших скоростях фильтрации закон Дарси перестает быть линейным.

В случае малых скоростей, проявляются неньютоновские свойства фильтрующихся жидкостей, а также другие физико-химические эффекты (действие межфазных и межмолекулярных сил). Для учета возникающих эффектов вводится поправка Клинкенберга.

В случае больших скоростей фильтрации, силы инерции фильтрующихся жидкостей становятся соизмеримыми с силами трения. Для учета данных эффектов используется закон Форхгеймера.

При проведении эксперимента по определению проницаемости также зачастую проводится и измерение пористости образцов.

Проницаемость горных пород (лекция). Закон Дарси

Общие сведения

В природе существует несколько видов силовых полей. Одним из них является магнитное поле (МП). В физике под ним понимают силу, действующую на перемещающиеся электрические заряды, обладающие магнитным моментом. Каждое тело в том или ином виде характеризуется восприимчивостью к такого роду полю.

Для понимания процесса можно провести эксперимент. Если взять кольцо индуктивности и пропустить через него электрический ток, то вокруг него возникнет электромагнитное поле. Если в катушку вставить железный сердечник, то магнитные свойства усилятся. Другими словами, железо усиливает магнитное поле, созданное током, протекающим по виткам. Получается, что появляется дополнительный источник магнетизма — железо. По принципу суперпозиции векторы источников складываются. Возникает усиленное поле.

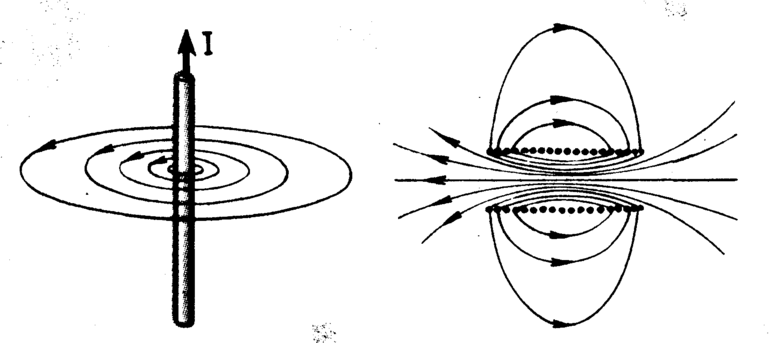
Допустим, магнитная индукция поля, создаваемая только током, имеет величину B0, а веществом — B1. Вектор магнитной индукции в материале будет складываться из этих двух величин: B = B0 + B1. Основываясь на эксперименте, физики решили ввести новую величину, которая характеризует, насколько вещество изменяет магнитное поле. Этот параметр было решено обозначить символом μ и назвать магнитной проницаемостью. Её единицей измерения стала безразмерная величина.

Таким образом, физический смысл магнитной проницаемости вещества заключается в величине, равной отношению модуля вектора магнитной индукции поля в материале к создаваемому теми же токами полю без дополнительных элементов. Для вакуума формула магнитной проницаемости имеет вид μ = B / B0. По сути параметр является магнитным аналогом диэлектрической проницаемости. Но если диэлектрики всегда ослабляют поле, то магнетики его усиливают.

На протяжении нескольких десятков лет различные физики проводили эксперименты над способностью материалов поддерживать распространение МП. В результате была построена таблица, в которую были занесены показатели, характерные для разных сред. Так, для воздуха параметр равняется 1.25663753*10−6, вакуума — 4π*10−7, дерева — 1.25663760*10−6, а чистого железа — 6.3*10−3. Все эти данные общедоступны. Их легко можно найти практически в любом физическом справочнике.

Свойство ферромагнетиков

С точки зрения физики наиболее интересным материалом является ферромагнетик. Существует устройство, представляющее собой кольцо из него. На прибор равномерно в один слой намотан провод, через который протекает электрический ток. В этом торе возникает электрическое поле, совпадающее по величине с вектором МП. В результате сердечник окажется намагниченным.

Если по оси ординат отложить магнитную индукцию тела, а по оси — абсцисс тока, то можно обнаружить следующие особенности:

• в начальный момент времени график будет возрастать примерно под углом 30 градусов;
• после достижения определённой величины (1 Тл) произойдёт резкое выравнивание графика относительно B0.

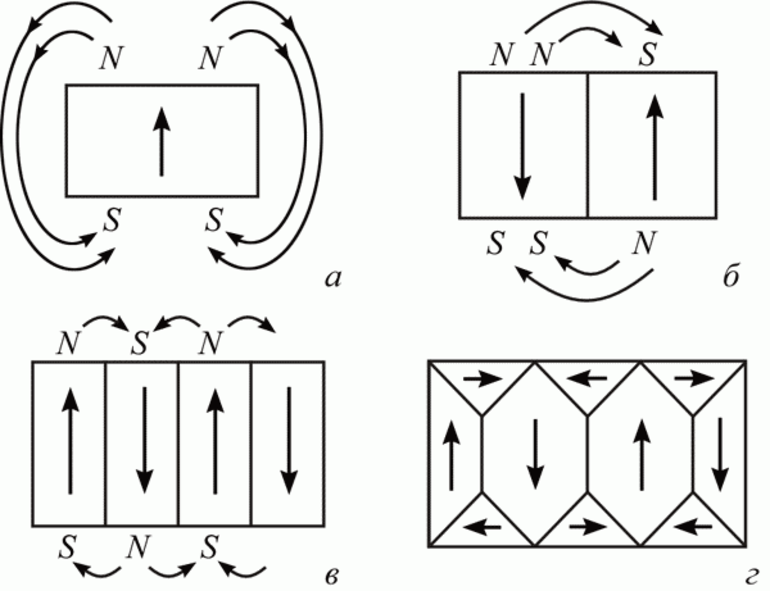
Из этого можно сделать вывод, что ферромагнетик примерно в тысячу раз увеличивает магнитное поле. Выходит, что магнитная проницаемость зависит от намагничивающего поля. Если провести перпендикуляры с точки перехода графика на координатные прямые и нарисовать из неё диагональ к нулевой точке, то тангенс угла к B0 будет равняться проницаемости: μ = tg j. Оказывается, что при больших намагничивающих полях МП перестаёт расти, то есть существует магнитное насыщение.

Если взять феррит и намагнитить его, а поле размагнитить путём уменьшения поля, то линия размагничивания будет другой. При исчезновении внешнего поля ферромагнетик останется намагниченным.

На петеле можно выделить две точки:

• Bo — остаточная магнитная индукция, возникающая после снятия электрического поля;
• Bc — коэрцитивная сила, индукция противоположно направленного поля.

Ферромагнетики, которые обладают широким гистерезисом, называются жёсткими. К ним относится закалённая сталь, сплавы альнико и магнико, неодим. Но бывают и ферромагнетики, которые довольно легко перемагнитить. Их петля гистерезиса имеет узкий вид. Используют такие материалы в электродвигателях, трансформаторах. Их называют мягкими. Примеры — отожжённая сталь, пермаллой.

Проницаемость горных пород

Способность горных пород пропускать через себя жидкости и газы называется проницаемостью. Любая горная порода при больших перепадах давлений может пропускать через себя жидкость или газ. Однако в условиях верхней части земной коры существуют породы, которые практически являются непроницаемы для жидкости и газа. К таким породам относятся плотные породы – соли, глины. 

Размеры, мм	Тип
	микро-поры	Поры	Каналы	Трещины
< 0.0002	Субкапиллярные	Субкапиллярные	Субкапиллярные
0.0002-0.001	Микропоры	Микропоровые	Микротрещины
0.001-0.01	Тонкие	Тонкопоровые	Волосяные
0.01-0.1	маккропоры	Очень мелкие	Очень мелкопоровые	Тонкие
0.1-0.25	Мелкие	Мелкопоровые	Мелкие
0.25-0.5	Средние	Среднепоровые	Средние
0.5-1	Крупные	Крупнопоровые	Крупные
1-2	Грубые	Грубопоровые	Грубые
2-20	каверны	Каверны мелкие	Мелкокаверновые	Макротрещины
20-100	Каверны средние	Среднекаверновые	Широкие
100-200	Каверны крупные	Крупнокаверновые	Весьма широкие
200-1000	пещеры	Пещеры мелкие
1000-2000	Пещеры средние
> 2000	Пещеры крупные

Проницаемость, закон Дарси

Проницаемость определяет способность породы отдавать жидкости и газы, содержащиеся в них, при перепадах давлений. Еще в середине XIX века проводились опыты по определению скорости фильтрации воды в песках. На основе таких опытов французский ученый Дарси установил закон фильтрации, названный его именем – закон Дарси: скорость фильтрации прямо пропорционально гидравлическому уклону, обратно пропорционально длине пути фильтрации.

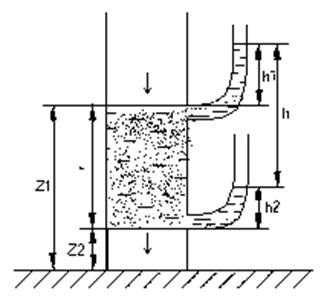где h₁, h₂ – высоты над нулевым уровнем,

Δl – расстояние между точками измерения (длина пути фильтрации)

Коэффициент пропорциональности называется коэффициентом фильтрации — К_ф. Он зависит от типа жидкости, от ее плотности – d, и динамической вязкости – μ.

Коэффициент пропорциональности при этом называется коэффициентом проницаемости — К_ПР. Он зависит от пористости пород.

Гидравлический уклон  можно выразить через давление: 

Тогда закон Дарси принимает вид:

Скорость фильтрации прямо пропорциональна перепаду давления жидкости на входе и на выходе из пористой породы, и обратно пропорциональна вязкости жидкости и длине пути фильтрации.

В системе СГС проницаемость измеряется в дарси (Д). За одно дарси принимается проницаемость, при которой через породу с поперечным сечением 1см2 и при перепаде давления 1 ат за секунду проходит 1 см3 жидкости вязкостью 1 сантипуаз (спз). Одна тысячная доля дарси называется миллидарси (мД). В системе СИ коэффициент проницаемости имеет размерность площади – м2, выражает площадь сечения поровых каналов. Один квадратный микрометр (1 мкм2) равняется 10-12 м2. Проницаемость 1 мкм2 соответствует фильтрации 1м3 жидкости за одну секунду через образец горной породы сечением 1м2, длиной 1м при перепаде давления 0,1 Мпа и динамической вязкости жидкости 1 мПа·с. Проницаемость 1 мкм2 соответствует 0,981 Д.

Зависимость между пористостью и проницаемостью прямая, но не линейная. При возрастании плотности пород проницаемость падает, особенно резко при достижении плотности 2 г/см3. Проницаемость зависит не только от общей пористости пород, но и от размеров и формы пор и каналов.

Проницаемость коллекторов нефти и газа изменяется в широких пределах – от 0,001 мкм2 до нескольких мкм2. Пласт называется хорошо проницаемым, если проницаемость его составляет единицы или десятые доли мкм2. Коэффициент проницаемости, замеренный в поверхностных условиях, значительно выше, чем коэффициент проницаемости, замеренный на глубине.

Эффективная пористость пород отсутствует при диаметре капилляров, равном 1 мкм. При диаметре каналов в десятые и сотые доли микрона струйное течение жидкости отсутствует, т.е. закон Дарси не соблюдается. Проникновение жидкости через такие породы происходит не по закону фильтрации, а по закону диффузии, т.е. на молекулярном уровне.

Определение проницаемости производится в лабораториях. Различают два вида проницаемости:

Гипотеза Ампера

С её помощью можно объяснить, почему одни вещества проявляют парамагнитные или диамагнитные свойства, а другие усиливают МП. Ампер провёл ряд экспериментов, сравнивая конфигурацию поля, создаваемого полосовым магнитом и катушкой с током. Было определено, что для полосового магнита характерна ситуация, когда линии потока выходят из северного полюса и входят в южный. Катушка же создаёт поле, похожее на конфигурацию МП постоянного полосового магнита.

Это сходство позволило Амперу предположить, что магнитные свойства веществ обусловлены тем, что внутри их существует своя проводимость, которая может убывать или возрастать в зависимости от внешних воздействующих факторов. Так, Ампер утверждал, что магнитные свойства материала объясняются существованием в его объёме микроскопических замкнутых электрических токов. Впоследствии его догадка была подтверждена. Такие токи названы молекулярными.

Другими словами, это электроны, движущиеся вокруг ядра в атоме. Для примера стоит рассмотреть гелий. В нём два электрона движутся по практически одинаковым орбитам, но только в противоположные стороны. Каждый из электронов несёт электрический заряд, создающий ток, следовательно, и поле. Если нарисовать их магнитные поля, то можно увидеть, что их направление будет противоположным: B1 + B2 = 0. Значит, атом гелия не создаёт вокруг себя МП. При помещении его во внешнее МП B0 к силе притяжения электрона прибавится сила Лоренца, направленная по радиусу от ядра.

Таким образом, сила притяжения к ядру ослабеет. Чтобы двигаться по той же самой орбите, электрону нужна меньшая скорость. Применительно ко второму электрону ситуация будет противоположной. Скорость электрона станет больше. В результате поле, создаваемое первым электроном, станет меньше, а вторым — больше. Следовательно, B1 + B2 ≠ 0. При этом гелий будет намагничиваться против внешнего поля, то есть является диамагнетиком.

Для парамагнетиков характерно то, что каждый атом обладает своим орбитальным полем. То есть атомы можно представить как витки с током. Если поля нет, направление электронов хаотичное. Причём их сумма будет равняться нулю. При помещении его во внешнее МП каждый свободный атом будет стремиться развернуться так, чтобы его нормаль была направлена по полю. Но при этом процессу мешает тепловое движение.

https://youtube.com/watch?v=4yLslpJ6pcA

Зависимость диэлектрической проницаемости от сторонних факторов

Следует заметить, что значение диэлектрической проницаемости зависит от частоты электрического поля (в данном случае – от частоты напряжения, приложенного к обкладкам). С ростом частоты значение ε у многих веществ падает. Этот эффект ярко выражен для полярных диэлектриков. Объяснить это явление можно тем, что заряды (диполи) перестают успевать следовать за полем. У веществ, для которых характерна ионная или электронная поляризация, зависимость диэлектрической проницаемости от частоты мала.

Поэтому так важен подбор материалов для выполнения диэлектрика конденсатора. То, что работает на низких частотах, не обязательно позволит получить качественную изоляцию на высоких. Чаще всего на ВЧ в качестве изолятора применяют неполярные диэлектрики.

Также диэлектрическая проницаемость зависит от температуры, причем у разных веществ по-разному. У неполярных диэлектриков она падает с ростом температуры. В этом случае для конденсаторов, выполненных с применением такого изолятора, говорят об отрицательном температурном коэффициенте ёмкости (ТКЕ) – ёмкость с ростом температуры падает вслед за ε. У других веществ проницаемость с ростом температуры увеличивается, и можно получить конденсаторы с положительным ТКЕ. Включив в пару конденсаторы с противоположными ТКЕ, можно получить термостабильную ёмкость.

Понимание сущности и знание значения диэлектрической проницаемости различных веществ важно для практических целей. А возможность управлять уровнем диэлектрической проницаемости даёт дополнительные технические перспективы

Закон Кулона, определение и формула — электрические точечные заряды и их взаимодействие

Что такое электрическая ёмкость, в чём измеряется и от чего зависит

Что такое конденсатор, где применяется и для чего нужен

Магнитное поле: источники, свойства, характеристики и применение

Что такое конденсатор, виды конденсаторов и их применение

В чём отличие проводников от диэлектриков, их свойства и сфера применения

Природа диэлектрической проницаемости

В основе природы диэлектрической проницаемости лежит явление поляризации под действием электрического поля. Большинство веществ в целом электрически нейтральны, хотя и содержат заряженные частицы. Эти частицы расположены в массе вещества хаотично и их электрические поля в среднем нейтрализуют друг друга.

В диэлектриках находятся, в основном связанные заряды (их называют диполями). Эти диполи условно представляют собой связки из двух разноименных частиц, которые по толщине диэлектрика ориентированы спонтанно и в среднем создают нулевую напряженность электрического поля. Под действием внешнего поля диполи стремятся сориентироваться согласно приложенной силе. В результате создается дополнительное электрическое поле. Сходные явления происходят и в неполярных диэлектриках.

В проводниках процессы похожие, только там имеются свободные заряды, которые под действием внешнего поля разделяются и также создают собственное электрическое поле. Это поле направлено навстречу внешнему, экранирует заряды и снижает силу их взаимодействия. Чем больше способность вещества к поляризации, тем выше ε.

Примечания и ссылки

1. (in) Стивен Уитакер, Метод усреднения , издательство Kluwer Academic Publishers ,2010 г., 471  с. ( ISBN  978-3-642-05194-4 )
2. (in) Люк Тартар, Общая теория гомогенизации , Springer ,2009 г., 210  с. ( ISBN  978-90-481-5142-4 )
3. (in) Питер Дж. Мор, Барри Н. Тейлор и Дэвид Б. Ньюэлл, на Национальном институте стандартов и технологий
4. Моник Форт, Франсуа Бетар, Жиль Арно-Фассетта, Динамическая геоморфология и окружающая среда , Арман Колин ,2015 г. , стр.  121
5. ↑ и
6. (in) Оливия Куиндро и Жерар Л. Виньоль, «  Оценка структурных и транспортных волокнистых свойств в композитных преформах C / C, оцифрованных с помощью рентгеновской CMT. Часть I. Получение изображения и геометрические свойства  » , Journal of Materials Research , vol.  20, п о  9,2005 г., стр.  2328-2339
7. (in) Жерар Л. Виньоль, О. Куиндро, Азита Ахмади и Доминик Бернар, «  Оценка геометрических и транспортных свойств волокнистой композитной преформы C / C, оцифрованной с помощью рентгеновской CMT. Часть II: теплогазотранспортные свойства  » , Journal of Materials Research , vol.  22, п о  6,2007 г., стр.  1537-1550
8. (in) Джерард Л. Виньолес и Альберто Ортона, «  Численное исследование эффективной теплопроводности пен, связанных за счет проводимости и излучения  » , International Journal of Thermal Sciences , Vol.  109,2016 г., стр.  270-278

Что такое диэлектрическая проницаемость

Согласно закону Кулона, два точечных неподвижных заряда q₁ и q₂ в вакууме взаимодействуют между собой с силой, заданной формулой F_кл=((1/4)*π* ε)*(|q₁|*|q₂|/r2), где:

• F_кл – сила Кулона, Н;
• q₁, q₂ – модули зарядов, Кл;
• r – расстояние между зарядами, м;
• ε– электрическая постоянная, 8,85*10-12 Ф/м (Фарад на метр).

Если взаимодействие происходит не в вакууме, в формулу входит ещё одна величина, определяющая влияние вещества на силу Кулона, и запись закона Кулона выглядит так:

F=((1/4)*π* ε* ε)*(|q₁|*|q₂|/r2).

Эта величина обозначается греческой буквой ε (эпсилон), она безразмерна (не имеет единицы измерения). Диэлектрическая проницаемость является коэффициентом ослабления взаимодействия зарядов в веществе.

Часто в физике диэлектрическая проницаемость используется совместно с электрической постоянной, в этом случае удобно ввести понятие абсолютной диэлектрической проницаемости. Она обозначается ε_a и равна ε_a= ε* ε. В этом случае абсолютная проницаемость имеет размерность Ф/м. Обычную проницаемость ε также называют относительной, чтобы отличить ее от ε_a.

Виды проницаемости и формулы

Восприимчивость к магнетизму зависит от вида среды и определяется её свойствами. Поэтому принято говорить о способности к проницаемости конкретной системы, имея в виду состав, состояние, температуру и другие исходные данные.

Существует четыре вида проницаемости:

1. Относительная. Характеризует, насколько взаимодействие в выбранной среде отличается от вакуума.
2. Абсолютная. Находится как произведение проницаемости на магнитную константу.
3. Статическая. Определяется с учётом коэрцитивной силы и магнитной индукции. При этом, чем большее значение имеет характеристика, тем меньше частота магнитных потерь. Отсюда следует, что статическая проницаемость зависит от температуры.
4. Дифференциальная. Устанавливает связь между малым увеличением индукции и напряжённости — μд = m * tgb. Это утверждение означает, что величина определяется по основной кривой намагничивания, из-за нелинейности которой она переменчивая.

Если среда однородная и изотропная, то проницаемость определяется по формуле:μ = В/(μoН), где: B — магнитная индукция; H — напряжённость; μo — константа. Постоянный коэффициент в формуле водится для записи уравнения магнетизма в рациональной форме для проведения расчётов. Знак его всегда постоянный. Он позволяет связать между собой относительную магнитную проницаемость и абсолютную.

Магнитная восприимчивость связана с проницаемостью простым выражением μ = 1 + χ. Эта формула справедлива, если все параметры будут измеряться в СИ. В единицах СГС равенство примет вид μ = 1 + 4πx. Например, проницаемость вакуума равняется единице, так как x = 0. Она безразмерна и помогает оценить способность намагничивания материала в МП.

Существует три вида восприимчивости: объёмная, удельная и молярная. Для диамагнетиков она отрицательная, а для парамагнетиков — положительная. При этом у ферромагнетиков её значения могут достигать тысяч единиц, в то время как для остальных классов веществ величина имеет очень малый порядок, около 10 -4 — 10 -6 .

Если на материал одновременно воздействует постоянное и переменное магнитное поле, то для описания процесса вводят дополнительное понятие — дифференциальную проницаемость. Наибольшее значение дифференциального параметра всегда будет превышать статическую составляющую μ = (1/μо)*(dB/dH). Эта формула по своему виду напоминает выражение, описывающее трение.

Патологическая физиология сосудистой проницаемости

Термином «сосудистая проницаемость» пользовались для обозначения гистогематического и транскапиллярного обмена, распределения веществ между кровью и тканями, тканевой П., гемолимфатического перехода веществ и других процессов. Некоторые исследователи применяют этот термин для обозначения трофической функции капилляро-соединительнотканных структур. Неоднозначность использования термина было одной из причин противоречивости взглядов по ряду вопросов, особенно касающихся регуляции сосудистой П. В 70-х гг. 20 в. термин «сосудистая проницаемость» стали использовать гл. обр. для обозначения избирательной проницаемости, или барьернотранспортной функции, стенок кровеносных микрососудов. Имеется тенденция к отнесению к сосудистой П. также и П. стенок не только микрососудов (кровеносных и лимфатических), но и крупных сосудов (вплоть до аорты).

Изменения сосудистой П. наблюдаются гл. обр. в форме повышения избирательной П. для макромолекул и клеток крови. Типичным примером этого является экссудация (см.). Понижение сосудистой П. связывают в основном с белковым пропитыванием и последующим уплотнением сосудистых стенок, что наблюдается, напр., при гипертонической болезни (см.).

Существует мнение о возможности нарушения П. сосудистой стенки преимущественно в направлении интерстиция или из интерстиция в кровь. Однако преимущественное движение веществ в ту или другую сторону относительно сосудистой стенки еще не доказывает его связь с состоянием барьерно-транспортной функции сосудистой стенки.

Формула расчета абсолютной проницаемости:

Единица
проницаемости в системе СИ – квадратный
метр (м²). На практике наиболее удобно использовать единицу дарси (darcy) (1 Д ≈ 10-12 м²). С
физической точки зрения, проницаемость характеризует площадь сечения каналов в
пористой среде, обеспечивающих фильтрацию при заданном давлении.

Тем не менее
многие породы (например, глины, сланцы и т.д.) в результате незначительности
размеров сообщающегося между собой порового пространства и низких давлениях
фильтрации, оказываются практически непроницаемыми для флюидов.

Для большинства пород нефтяных и газовых пластов проницаемость изменяется от нескольких миллидарси до нескольких сотен милидарси, причем ннизкопроницаемыми пластами считаются пласты с проницаемостью 0 – 100 мД, среднепроницаемыми – 100 – 500 мД и высокопроницаемыми – пласты с проницаемостью более 500 мД.

При
проведении экспериментов по замеру проницаемости также следует учитывать анизотропию проницаемости:

Горизонтальная проницаемость для большинства коллекторов больше, чем вертикальная (длинные и плоские стороны зерен отлагаются горизонтально)

Разделение веществ

В пятидесятые годы девятнадцатого столетия Фарадей исследовал влияние веществ на МП. В итоге он пришёл к выводу, что все материалы без исключения влияют на поле. Отсюда следует, что любое вещество является источником своего МП, но при условии его помещения во внешнее поле. Это явление было названо намагниченностью.

По результатам своего исследования Фарадей разделил все физические элементы на три класса, дав определение каждому из них:

1. Диамагнетики. Вещества, у которых проницаемость чуть меньше единицы: μ < 1. К ним относятся все газы, кроме кислорода, золота, серебра, углерода в любой кристаллической модификации, висмута. При помещении этих веществ в МП собственный вектор магнитной индукции направлен в сторону противоположную вектору, создаваемому током: B1↑↓B0. C другой стороны, так как значение B1 близко к единице, то модуль вектора B1 гораздо меньше модуля B0. Получается, что такое вещество намагничивается очень слабо и против внешнего поля. Интересным фактом является то, что диамагнетики при помещении в катушку с МП выталкиваются из неё.
2. Парамагнетики. К ним относят материалы, у которых магнитная проницаемость немного больше единицы. Например, щелочные металлы, алюминий вольфрам, магний, платина. Для этих веществ характерно то, что модуль B1 параллелен вектору B0, но при этом модуль B1 меньше, чем модуль вектора B0.
3. Ферромагнетики. К этому классу относят материалы, у которых μ намного больше единицы. Классическими представителями таких веществ являются: железо, никель, кобальт и их сплавы. Эти вещества намагничиваются вдоль поля. При этом B1 по модулю гораздо больше B0. Такие материалы сильно увеличивают магнитное поле.

В однородном МП на тело, обладающее магнитным моментом, действует только момент сил, который стремится развернуть диполь вдоль направления силовых линий. В неоднородном поле на диполь будет дополнительно действовать сила, пропорциональная величине дипольного момента и градиента поля: F = P (dB/dn) * cosj.

Определения

Определение допущений

Предположение, лежащее в основе определения, состоит в том, что течение в среде является стоксовым потоком . Это предположение используется для установления уравнения Дарси из описания пористости методом объемного усреднения или гомогенизации . Проницаемость — это свойство среды и, следовательно, не зависит от жидкости, проходящей через нее, жидкости или газа. Это должно быть квалифицировано тем фактом, что физические явления, характерные для газов, могут возникать в средах с низкой пористостью, явления, описываемые уравнением Дарси-Клинкенберга . Таким же образом вязкость жидкости может влиять на высокие скорости потока, это зависит от числа Рейнольдса, сформированного с характерным размером пористости. Эта поправка к закону Дарси содержится в законе .

Определение изотропного материала

Для изотропного пористого материала, пересекаемого потоком, коэффициент проницаемости k является скалярным значением, определяемым из закона Дарси, дающего массовый расход q или среднюю скорость в среде V _f (скорость фильтрации) жидкости с плотностью ρ и кинематической вязкостью. ν под действием градиента давления ∇ p и гравитационного поля g  :

qзнак равноρVжзнак равно-kν(∇п-ρграмм){\ Displaystyle \ mathbf {q} = \ rho \ mathbf {V_ {f}} = — {\ frac {k} {\ nu}} (\ mathbf {\ nabla} p- \ rho \, \ mathbf {g} )}

k — размер поверхности. Таким образом, стандартная единица проницаемости — м 2 .

Для материала, который является изотропным, но не однородным по шкале пористости, коэффициент проницаемости является статистическим распределением, от которого обычно сохраняется только среднее значение.

Общее определение

Для однородного, но не изотропного материала коэффициент проницаемости является тензором, определяемым тем же уравнением, что и выше. Например, для поперечно-изотропной стратифицированной среды тензор проницаемости будет записан (ось z перпендикулярна пластам):

kзнак равно(kkk⊥){\ displaystyle {\ mathsf {k}} = {\ begin {pmatrix} k _ {//} & 0 & 0 \\ 0 & k _ {//} & 0 \\ 0 & 0 & k _ {\ perp } \\\ конец {pmatrix}}}

В общем случае проницаемость среды описывается 5 параметрами: 3 коэффициентами проницаемости и 2 углами ориентации этой среды относительно собственных осей материала.

Гидравлическая проводимость

В гидравлическом поле, где градиент давления q пренебрежимо мал , V _f и g выровнены, и это выражение записывается в скалярной форме:

qзнак равноρVжзнак равноkνρграммзнак равноρK{\ displaystyle q = \ rho V_ {f} = {\ frac {k} {\ nu}} \, \ rho \, g = \ rho K}

Это выражение определяет гидравлическую проводимость K (скорость фильтрации).

Нестандартный юнит: дарси

Дарси (символ D) определяется как проницаемость среды, в которой жидкость с вязкостью 1 сантипуаз (вода при 20 ° C), подверженная градиенту давления 1 атм, течет со скоростью 1 см / с. -1

Принимая во внимание определение единицы атмосферы p = 1,01325 × 10 5 Па и преобразование других единиц (см, сантипуаз), имеем:

1D знак равно 10-3×10-2×10-21.01325×105 м2 знак равно 0,9869 …×10-12 м2 ≃ 1 μм2{\ displaystyle \ scriptstyle 1D ~ = ~ {\ frac {10 ^ {- 3} \ times 10 ^ {- 2} \ times 10 ^ {- 2}} {1.01325 \ times 10 ^ {5}}} ~ m ^ {2} ~ = ~ 0,9869 … \ times 10 ^ {- 12} ~ m ^ {2} ~ \ simeq ~ 1 ~ \ mu m ^ {2}}

Дарси, хотя и все еще используется, является устаревшим устройством.

Этиопатогенетические основы профилактики и лечения нарушений сосудистой проницаемости

Направленное вмешательство осуществляется на трех уровнях (см. схему). Первый уровень — воздействие на процесс образования причинных (рецептируемых) факторов — практически не используется, хотя имеются отдельные медикаментозные средства, способные действовать именно на этом уровне. Напр., резерпин влияет на депонирование факторов нарушения П. в тучных клетках, представляющих собой основной источник медиаторов острого воспаления (гистамина и серотонина); антипростагландиновые средства угнетают синтез простагландинов — ацетилсалициловая кислота и др.

Второй уровень является основным в практике разработки средств профилактики и лечения нарушений сосудистой П. Он соответствует процессу рецепции причинного фактора. Используется значительное число антигистаминовых, антисеротониновых и антибрадикининовых препаратов, предупреждающих нарушения сосудистой П., вызываемые соответствующими медиаторами. Достоинством и в то же время недостатком данных препаратов, действующих путем блокады специфических рецепторов, является их высокая специфичность. Такая специфичность делает их неэффективными в условиях множественности этиол. факторов, действующих одновременно или последовательно, что обычно наблюдается в клин. практике

Важно и то, что исключение действия одного фактора или нескольких, определяющих развитие одной фазы нарушения сосудистой П., не исключает развитие последующих фаз. Эти недостатки могут быть преодолены путем вмешательства на третьем уровне.

Третий уровень — воздействие на внутриклеточные (субклеточные) эффекторные механизмы, через которые непосредственно реализуется действие факторов П., причем единые для действия различных патогенных агентов. Реальность и эффективность такого подхода удается продемонстрировать в эксперименте путем применения вещества (цитохалазина-Б), угнетающего феномен оперативной структурализации микрофибриллярного аппарата в эндотелиоцитах (образование актинового геля и актиновых микрофибрилл).

В клин. практике с целью нормализации повышенной сосудистой П. используют витамин P (см. Биофлавоноиды) и соли кальция. Однако эти препараты не могут рассматриваться как специфические лечебные средства при нарушении сосудистой Проницаемости, хотя они и оказывают общеукрепляющее влияние на гистогематические барьеры, мембраны и стенку сосудов в частности.

Для повышения сосудистой П. могут быть использованы различные эндогенные факторы П., напр. гистамин, или вещества, освобождающие их из тканевых депо.

Библиография: Алексеев О. В. Микроциркуляторный гомеостаз, в кн.: Гомеостаз, под ред. П. Д. Горизонтова, с. 278, М., 1976; Антонов В. Ф. Липиды и ионная проницаемость мембран, М., 1982; Биологические мембраны, под ред. Д. С. Парсонса, пер. с англ., М., 1978; Де Робертис Э., Новинский В. и Саэс Ф. Биология клетки, пер. с англ., М., 1967; Живая клетка, пер. с англ., под ред. Г. М. Франка, с. 130, М., 1962; Казначеев В.П. и Дзизинский А. А. Клиническая патология транскапиллярного обмена, М., 1975; Лайтфут Э. Явления переноса в живых системах, пер. с англ., М., 1977; Лакшминараянайах Н. Мембранные электроды, пер. с англ., Л., 1979; Лев А. А. Моделирование ионной избирательности клеточных мембран, Л., 1976; Овчинников Ю. А., Иванов В. Т. и Шкроб А. М. Мембранно-активные комплексоны, М., 1974; Структура и функция клетки, пер. с англ., под ред. Г. М. Франка, с. 173, М., 1964; Трошин А. С. Проблема клеточной проницаемости, М. — Л., 1956; Чернух А. М., Александров П. Н. и Алексеев О. В. Микроциркуляция, М., 1975; Di Rosa М., Giroud J. Р. а. Willoughby D. A. Studies of the mediators of the acute inflammatory response induced ln rats in different sites by carra-geenan and turpentine, J. Path., v. 104, p. 15, 1971; Majnо G. а. Pаlade G. E. Studies on inflammation, I. The effect of histamine and serotonin on vascu-lar permeability, an electron microscopic study, J. biophys. biochem. Cytol., v. 11, p. 571, 1961; Majnо G., Shea S. M. a. Leventhal M. Endothelial cont-raction induced by histamine-type mediators, J. Cell Biol., v. 42, p. 647, 1969: Shimamoto T. Contraction of endothelial cells as a key mechanism in athero-genesis and treatment of atherosclerosis with endothelial cell relaxants, в кн.: Atherosclerosis III, ed. by G. Schettler a. A. Weizel, p. 64, В.—N. Y., 1974.

B. Ф. Антонов; О. В. Алексеев (пат. физ.).

Расчеты

Микротомография композита Ti ₂ AlC / Al.

Расчет основан на знании или моделировании пористости.

Можно смоделировать проблему, сведя ее к задачам, аналитическое решение которых известно:

• параллельные цилиндрические пористости и использование закона Пуазейля ,
• множество сфер, к которым применим закон Стокса .

Параметры (размер, интервал) выбираются с учетом имеющихся у нас дополнительных сведений, как правило, о пористости. Таким образом, мы получаем закон Козени-Кармана или закон Эргюн .

В последнее время методы микротомографии позволили восстановить точную геометрию среды и, следовательно, выполнить точный расчет проницаемости. Этот расчет выполняется для различных блоков, определенных в материале, и обеспечивает доступ к статистическому распределению этого свойства. Кроме того, этот метод, конечно, позволяет рассчитать пористость, а также другие параметры, такие как кажущаяся теплопроводность по проводимости, а также по излучению.