Зависимые и независимые выборки
При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:
·пары близнецов,
·два измерения какого-либо признака до и после экспериментального воздействия,
·мужья и жёны
·и т. п.
В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:
·мужчины и женщины,
·психологи и математики.
Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.
Сравнение выборок производится с помощью различных статистических критериев:
·t-критерий Стьюдента
·Критерий Уилкоксона
·U-критерий Манна-Уитни
·Критерий знаков
·и др.
Как выбирать?
Есть несколько способов собрать репрезентативную выборку.
Простая случайная выборка (simple random sample)
Случайным образом выбираем объекты нашей генеральной совокупности. При этом чем больше случайных объектов выбираем, тем лучше наша выборка отражает свойства генеральной совокупности
На Примере 2: Идем на детскую площадку и опрашиваем всех, кто там есть. В результате получится, что среди опрошенных будут дети разного пола и возраста в разной пропорции. Например, мы спросили о любимом мультфильме мальчика пяти лет, девочку трех лет, девочку четырех лет, мальчика двух лет и.т.д.
Стратифицированная выборка (stratified sample)
- Разделяем нашу генеральную совокупность на группы (страты) на основе определенного признака/признаков.
- Чтобы эти группы были равновероятно представлены в выборке, берем случайным образом элементы из каждой группы с равной вероятностью.
На Примере 2: делим детей по возрасту и полу, «идем» в группу «мальчики 5 лет» , случайно опрашиваем представителя данной группы, потом идет ко множеству «девочки 3 лет», случайно опрашиваем представительницу этой группы и т.д.
В таблице суммируются принципиальные различия между случайной и стратифицированной выборками:
| Простая случайная выборка | Стратифицированная выборка |
| Выбираем элементы из генеральной совокупности случайным образом | Выбираем элементы из каждой группы (страты) |
| Чем больше берем элементов из генеральной совокупности, тем лучше наша выборка отражает особенности генеральной совокупности | Мы уже на основе определенных признаков разделили нашу генеральную совокупность, добавляем в каждую подгруппу по примерно равному количеству элементов. Так наша выборка будет хорошо отражать особенности генеральной совокупности |
Групповая выборка (cluster sample)
- Делим нашу генеральную совокупность на группы, но эти группы должны быть относительно похожи между собой (в качестве примера можем взять районы Москвы и считать, что в них примерно одинаковое число жителей)
- Выбираем только некоторые группы, которые нас интересуют.
- Из выбранных групп выбираем случайным образом элементы.
Чтобы еще лучше понять, чем отличается стратифицированная выборка от групповой, рассмотрим таблицу:
| Стратифицированная выборка | Групповая выборка |
| Выбираем элементы из каждой группы (страты) | Выбираем элементы только из выбранных групп (страт) |
| Внутри группы элементы однородны, а между группами элементы различаются | В пределах группы элементы разнородны, но при этом все группы имеют схожесть |
| Схема выборки для всех групп одна | Схема выборки нужна только для выбранных групп |
| Повышает точность | Повышает эффективность выборки, уменьшая стоимость |
Сбор репрезентативной выборки — это нетривиальная задача, которая включает в себя выбор метода сбора и параметров сбора (например, подбор страт). Аккуратно собранная выборка — обязательное условие для проведения дальнейшего исследования
Использование нерепрезентативных данных приводит к ложным или неполным выводам, поэтому крайне важно обращать внимание, на каких данных проводилось то или иное исследование
Двухвыборочный t-критерий для независимых выборок
Для двух
несвязанных выборок(наблюдения не относятся к одной и той же группе
объектов ) возможны два варианта расчета:
-
-
когда дисперсии известны
-
когда дисперсии неизвестны, но равны друг
другу.
-
-
Предварительно проверяется нормальность закона
распределения по одному из критериев согласия. -
Рассчитывается средне арифметические значенияидля
каждой выборки по формулегде–
значениеi-го
результата наблюдения. -
Рассчитывается-
эмпирическое значение критерия Стьюдента:
Гдеквадратичного отклонения. Здесьи–
оценки дисперсий.
Рассмотрим
сначала равночисленные выборки. В этом случаеВ случае наравночисленных выборок,
выражение
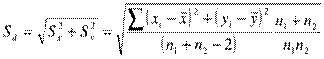В обоих случаев подсчет числа
степеней свободы осуществляется по формуламПонятно, что при численном равенстве
выборок
Эмпирическое значениекритерия
Стьюдента сравнивается с критическим значением(по таблице 1
приложения) для данного числа степеней свободы.
Нулевая
гипотезапри
заданном уровне значимостипринимается,
если эмпирическое значение.
Пример рассчитаем на лабораторной работе.
Пример.Психолог
измерял время сложной сенсомоторной реакции выбора (в мс) в
контрольной и экспериментальных группах. В экспериментальную группу
(Х) входило 9 спортсменов высокой квалификации. Контрольной группой
(Y) являлись 8 человек, активно не занимающиеся спортом. Психолог
приверяет гипотезу о том , что средняя скорость сложной
сенсомоторной реакции выбора у спортсменов выше, чем та же величина
у людей, не занимающихся спортом.
|
|
|
|
|
|||
По таблице приложения для данного числа степеней
находим
Строим ось значимости
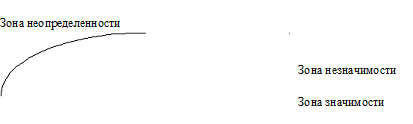
Под связанными выборками понимаются наблюдения для
одной группы объектов, причем все наблюдения попарно связаны с
каждый объектом исследования и характеризуют его состояние до
воздействия и после воздействия некоторого фактора.
|
Данные в выборке измерены по шкале интервалов Сравниваемые данные должны иметь нормальный Сравниваемых выборок две для оной группы |
1.
Предварительно проверяется нормальность закона
распределения по одному из критериев согласия.
2.
Рассчитывается(i=1..n)
– попарные разности вариант,ирезультаты
измерений дляi-го
объекта до и после воздействия некоторого фактора. Величинубудем
считать независимой для разных объектов и нормально распределенной
3.
Рассчитываются (лучше в табличной форме): сумма
попарных разностейи
вспомогательные параметрыи.
4.
Рассчитывается-
эмпирическое значение критериястепенями
свободы по формуле
Где n –
численность выборки.
5.Найденное
эмпирическое значениекритерия
Стьюдента сравнивается с критическим значением(по
таблице 1 приложения) для данного числа степеней свободы.Нулевая гипотезапри
заданном уровне значимостипринимается,
если эмпирическое значение.
Критическое значение для выбранной вероятности и
заданного числа степеней свободы можно найти по встроенной в Excel
функции СТЬЮДРАСПОБР.
Пример.Психолог
предположил, что в результате тренировки, время решения
эквивалентных задач (т.е. имеющих один и тот же алгоритм решения )
будет значительно уменьшаться. Для проверки гипотезы у восьми
испытуемых сравнивалось время решения (в минутах) первой и третьей
задачи.
Решение задачи
представим в таблице.
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
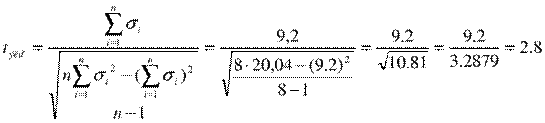Число степеней свободы=8-1=7.
По таблице Приложения находим
Строим ось значимости
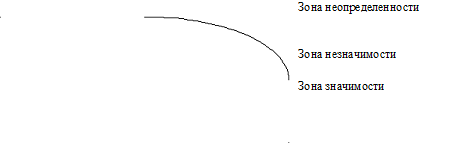
Т.о. на 5% уровне значимости,
первоначальное предположение подтвердилось, действительно, среднее
время решения 3-ей задачи, существенно меньше времени решения 1-ой
задачи. В терминах статистических гипотез полученный результат будет
звучать так: на5% уровне гипотеза Н0 отклоняется и принимается
гипотеза Н1 о различиях.Критерий
Фишера.
Критерий используется для сравнения дисперсий двух
выборок с нормальным распределением.Сравнения
дисперсий двух выборок производятся по отношению большей по величине
дисперсии(записывается в числителе) к меньшей (записывается в
знаменателе). Поэтому значения критерия больше или равно 1,0.
Гипотезы
:
Дисперсия выборке 1 не отличается от дисперсии в выборке 2:
Дисперсия выборке 1 отличается от дисперсии в выборке 2ОграниченияДанные в выборках должны быть
измерены по шкале интервалов или по шкале отношений.Обе сравниваемые выборки должны
иметь нормальный закон распределения.
Генеральная совокупность
Давайте разберемся, на что в первую очередь обращать внимание перед началом любой исследовательской или аналитической работы, какие вообще данные следует использовать,
Для начала нам нужно четко обозначить, для какого множества объектов мы хотели бы получить результаты экспериментов или исследований. То есть, что мы будем считать генеральной совокупностью нашего исследования.
Генеральная совокупность — это множество всех объектов, относительно которых предполагается делать выводы в рамках конкретного исследования. Генеральную совокупность составляют все объекты, которые отвечают всем заранее заданным параметрам.
Почему это важно? Разберем на конкретных примерах
Пример 1
Хотим узнать средний рост у космонавтов, находившихся в космическом полете более 180 дней.
Так как под такое описание подходит небольшая группа людей (а именно космонавты, которые пробыли в полете более 180 дней), мы можем провести исследование с участием всех представителей этого класса. Они и будут составлять генеральную совокупность нашего исследования.
Пример 2
Хотим изучить, какой мультфильм является самым любимым у детей до 5 лет, живущих в Москве.
В данной ситуации абсолютно все дети в возрасте до 5 лет, которые живут в Москве, будут представлять генеральную совокупность для нашего исследования.
Очевидно, что в исследовании из Примера 1 мы можем измерить рост каждого космонавта и получить желаемый результат.
В Примере 2 все становится несколько затруднительнее: теоретически мы, конечно, можем опросить каждого ребенка из Москвы в возрасте до 5 лет, но это сложно реализуемая затея.
Что тогда делать? Можно взять только определенную часть генеральной совокупности, то есть сформировать выборку для исследования, а затем обобщить результаты, полученные на этой выборке, на всю генеральную совокупность.
Что такое статистическая выборка из генеральной совокупности данных
Чтобы получить верную информацию об общем, в аналитической статистике изучают его частное. Этот метод называют статистической выборкой из генеральной совокупности данных.
Генеральная совокупность – это весь набор объектов, о которых необходимо получить информацию.
К примеру, это могут быть все жители Москвы за 1900-ый год, все российские компании одной отрасли производства за 2000-ый год и так далее. Иначе говоря, это суммарная численность объектов исследования, обладающая набором определённых признаков и ограниченная в пространстве и времени.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Однако не всегда можно получить данные обо всех объектах сразу. Исходя из экономии времени и средств, проводится исследование части набора, которая называется выборкой.
Выборка – это небольшой набор объектов, который извлекают из генеральной совокупности.
Из генеральной совокупности разными способами по разным признакам можно отобрать бесконечное множество выборок.
Понятия, как соотносятся между собой
Математически генеральная совокупность обозначается как N, выборочная – как n. Таким образом, случайная выборка n1, n2, …, nx – это результат последовательных и независимых наблюдений над случайной величиной N.
Стратегии построения групп
Отбор групп для их участия в психологическом эксперименте осуществляется с помощью различных стратегий, которые нужны для того, чтобы обеспечить максимально возможное соблюдение внутренней и внешней валидности.
·Рандомизация (случайный отбор)
·Попарный отбор
·Стратометрический отбор
·Приближённое моделирование
·Привлечение реальных групп
Рандомизация, или случайный отбор, используется для создания простых случайных выборок. Использование такой выборки основывается на предположении, что каждый член популяции с равной вероятностью может попасть в выборку. Например, чтобы сделать случайную выборку из 100 студентов вуза, можно сложить бумажки с именами всех студентов вуза в шляпу, а затем достать из неё 100 бумажек — это будет случайным отбором (Гудвин Дж., с. 147).
Попарный отбор — стратегия построения групп выборки, при котором группы испытуемых составляются из субъектов, эквивалентных по значимым для эксперимента побочным параметрам. Данная стратегия эффективна для экспериментов с использованием экспериментальных и контрольных групп с лучшим вариантом — привлечением близнецовых пар (моно- и дизиготных), так как позволяет создать…
Стратометрический отбор — рандомизация с выделением страт (или кластеров). При данном способе формирования выборки генеральная совокупность делится на группы (страты), обладающие определёнными характеристиками (пол, возраст, политические предпочтения, образование, уровень доходов и др.), и отбираются испытуемые с соответствующими характеристиками.
Приближённое моделирование — составление ограниченных выборок и обобщение выводов об этой выборке на более широкую популяцию. Например, при участии в исследовании студентов 2-го курса университета, данные этого исследования распространяются на «людей в возрасте от 17 до 21 года». Допустимость подобных обобщений крайне ограничена.
Приближенное моделирование – формирование модели, которая для четко оговоренного класса систем (процессов) описывает его поведение (или нужные явления) с приемлемой точностью.
Репрезентативность
Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.
Пример нерепрезентативной выборки
В США одним из наиболее известных исторических примеров нерепрезентативной выборки считается случай, происшедший во время президентских выборов в 1936 году. Журнал «Литрери Дайджест», успешно прогнозировавший события нескольких предшествующих выборов, ошибся в своих предсказаниях, разослав десять миллионов пробных бюллетеней своим подписчикам, а также людям, выбранным по телефонным книгам всей страны и людям из регистрационных списков автомобилей. В 25 % вернувшихся бюллетеней (почти 2,5 миллиона) голоса были распределены следующим образом:
·57 % отдавали предпочтение кандидату-республиканцу Альфу Лэндону
·40 % выбрали действующего в то время президента-демократа Франклина Рузвельта
На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и высшего класса (то есть большинство республиканцев, а не демократов).
