Идеальный газ в однородном поле тяготения. Барометрическая формула. Распределение Больцмана
Если бы не было
теплового движения, то все молекулы
атмосферного воздуха упали бы на Землю;
если бы не было тяготения, то атмосферный
воздух рассеялся бы по всей Вселенной.
Тяготение и тепловое движение приводят
газ в состояние, при котором его
концентрация и давление убывают с
высотой.
Получим закон
изменения давления с высотой.
Разность давлений
р
иp+
dp
равна весу газа,
заключенному в объеме цилиндра с площадью
основания, равной единице, и высотой dh
p
–
(p
+
dp
)
=
g
dh
dp
= –
g
dh
(10)
Из уравнения
состояния идеального газа:
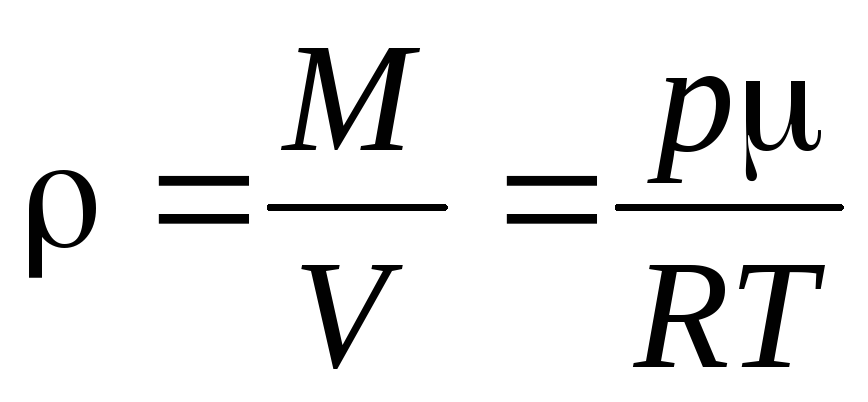(11)
(11)
(10)
,
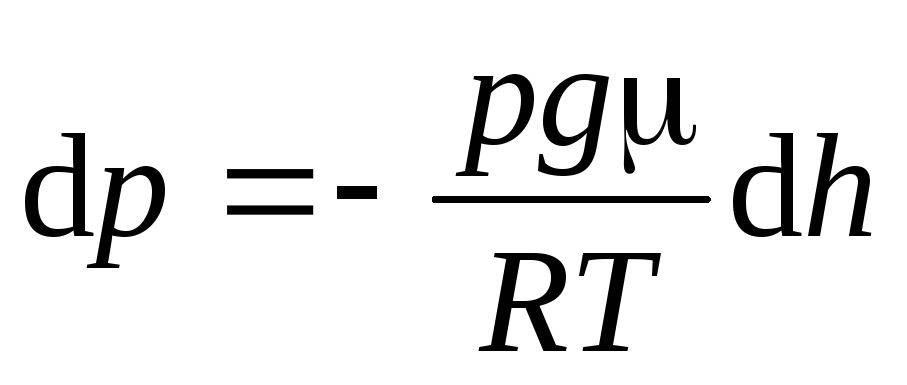
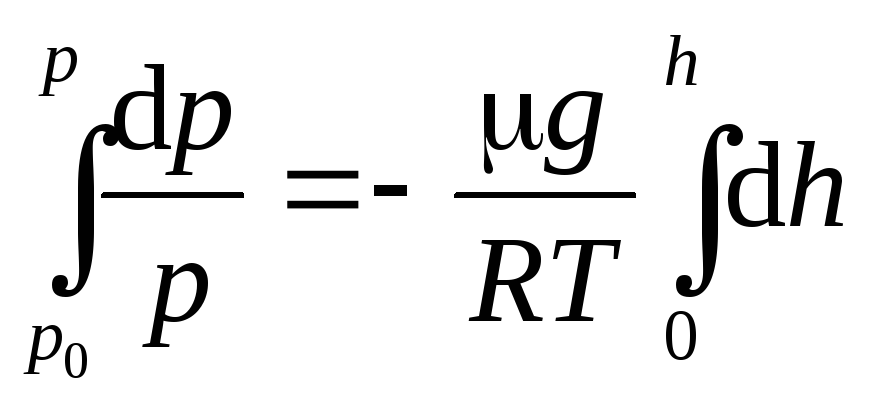
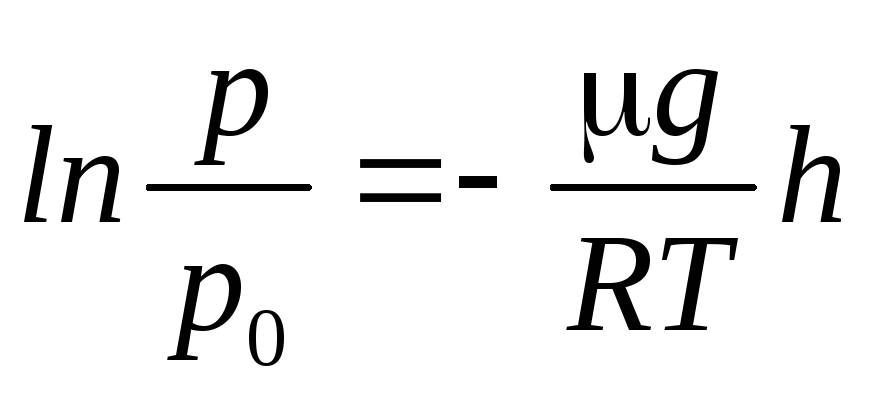
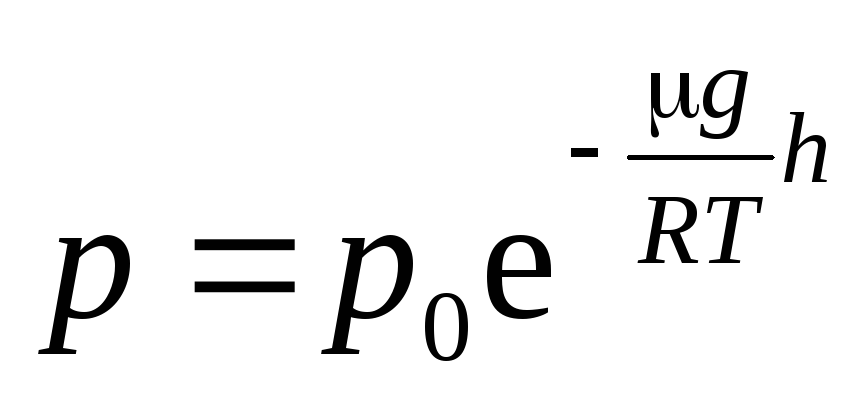(12)
где р
ир
0
– давления газа на высотахh
иh
= 0.
Формула (12) называется
барометрической
. Из нее следует,
что давление убывает с высотой по
экспоненциальному закону.
Барометрическая
формула позволяет определять высоту h
с помощью барометра. Барометр, специально
проградуированный, для непосредственного
отсчета высоты над уровнем моря называютальтиметром
. Его широко применяют
в авиации, при восхождении на горы.
Обобщение
барометрической формулы
,
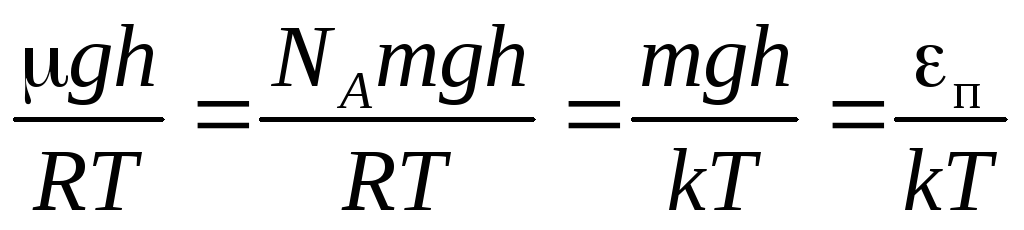так как
.
,
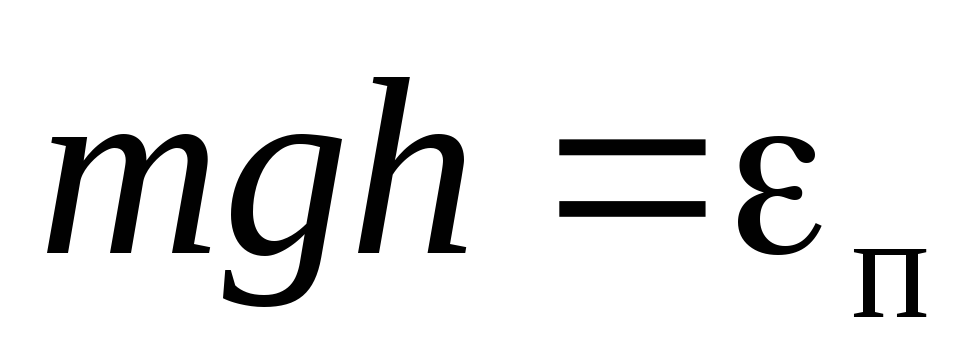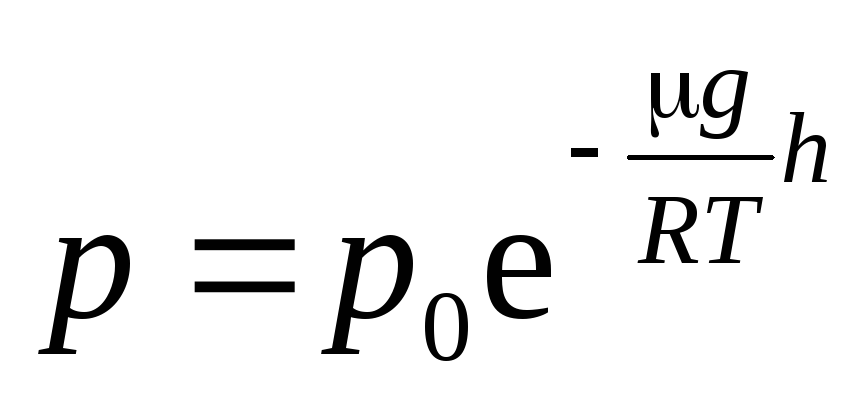
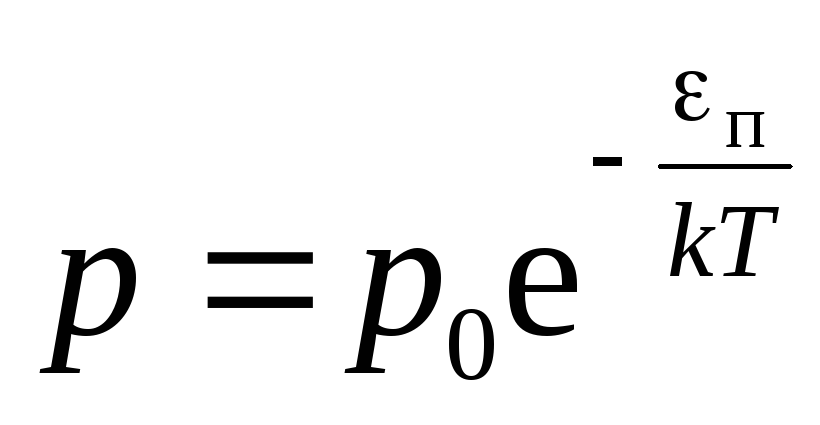
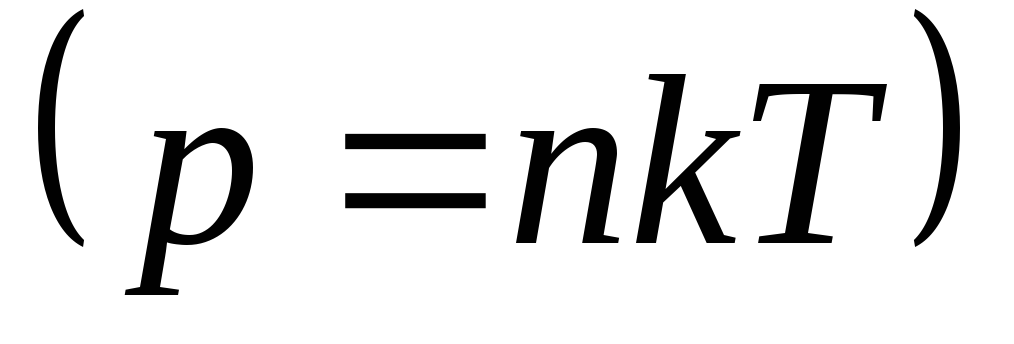
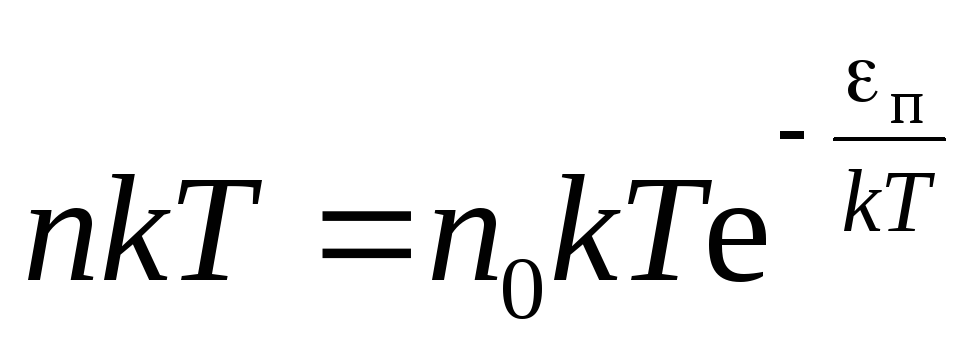
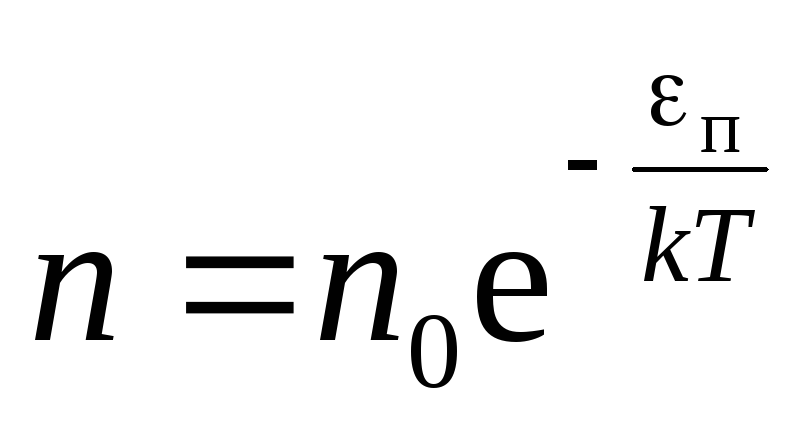распределениеБольцмана(13)
где n
иn
0 – концентрации молекул на высотахh
0 иh
= 0
соответственно.
Частные случаи
1.
,
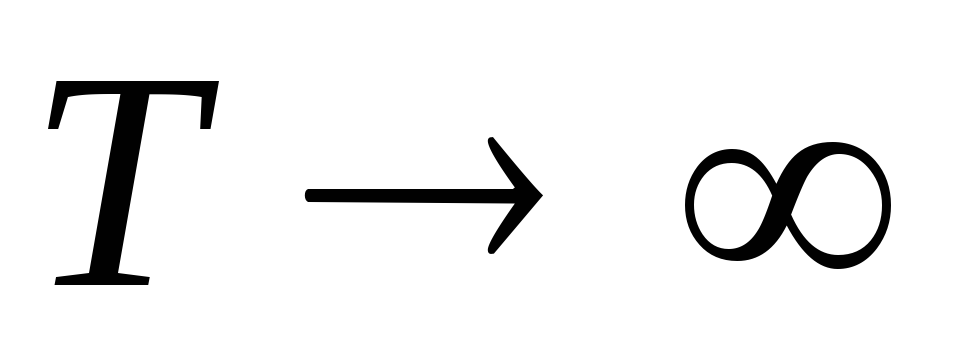
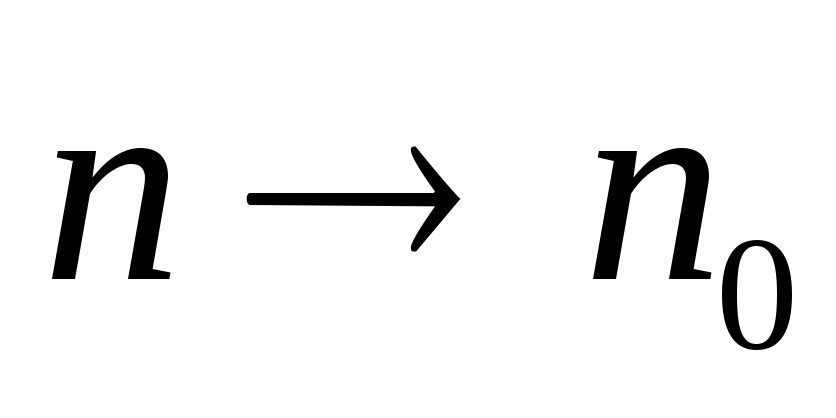т.е. тепловое движение стремится
разбросать частицы равномерно по всему
объему.
2.
(отсутствие теплового движения), т.е.
все частицы занимали бы состояние с
минимальной (нулевой) потенциальной
энергией (в случае поля тяготения Земли
молекулы собирались бы на поверхности
Земли).
Закон распределения Максвелла
Кратко опыт Штерна можно определить как визуализацию распределения скорости теплового движения атомов и молекул. При осаждении серебра на стенках внешнего цилиндра, когда система находится в состоянии покоя, получалась полоска с достаточно четкими краями. При вращении цилиндров она выходила размытой.
Причина этого – различие в скорости движения атомов, испускаемых при испарении серебряного покрытия проволоки. Более быстрые частицы осаждались с меньшим смещением от прорези в малом цилиндре, а те, что двигались медленнее, успевали преодолеть большее расстояние. Соотношение скоростей укладывается в пропорцию, предсказанную вычислениями Максвелла. Кривая поперечного сечения полученного напыления совпадает по форме с графическим выражением формул, послуживших основой молекулярно-кинетической теории.
Теория, проверенная практикой
Большое значение, которое имеет экспериментальная физика, опыт Штерна показывает особенно наглядно. Умение найти способ доказательства правильности теоретических постулатов особенно ценно, когда предметом научных исследований становятся объекты, неразличимые невооруженным глазом.
Последующая история науки, когда физика вступила в фазу исследования строения атома в период поиска элементарных частиц, доказала это. Одним из пионеров нового течения был немецкий физик, гениальный экспериментатор Отто Штерн.
-
Биография бокова ахмеда кратко
-
Выявить связь видового богатства с различными факторами кратко
-
Сша в период от войны за независимость до гражданской войны кратко
-
Прорыв линии зигфрида кратко
- Церковь сен дени кратко
Отрывок, характеризующий Опыт Штерна
общем плане
Лекция 15
Молекулярная
физика
Вопросы
1.
Закон Максвелла распределения молекул
идеального газа по скоростям и энергиям.
2.
Идеальный газ в однородном поле тяготения.
Барометрическая
формула. Распределение Больцмана.
3.
Среднее число столкновений и средняя
длина свободного пробега молекул.
4. Явления переноса
в газах.
1. Закон Максвелла
распределения молекул
идеального газа
по скоростям и энергиям
В газе, находящемся
в состоянии равновесия, устанавливается
стационарное распределение молекул по
скоростям, подчиняющееся закону
Максвелла.
Уравнение Клаузиуса
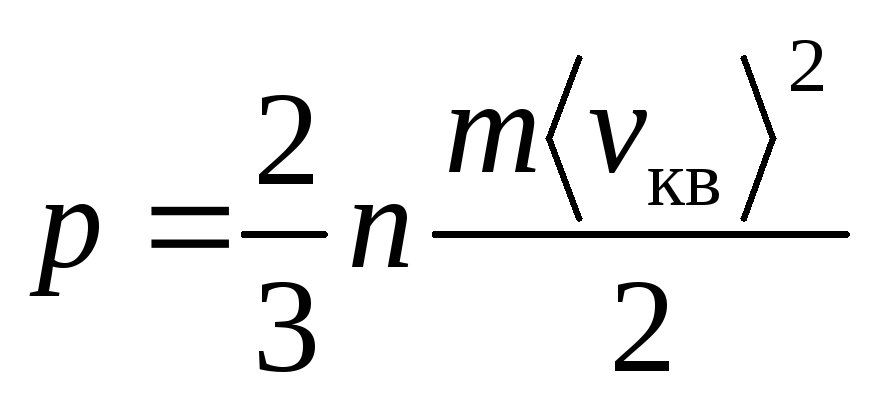, (1)
Уравнение Менделеева
– Клапейрона
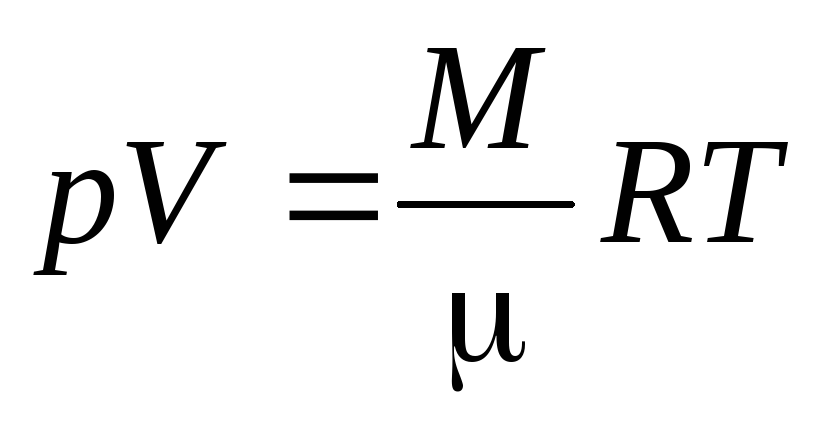
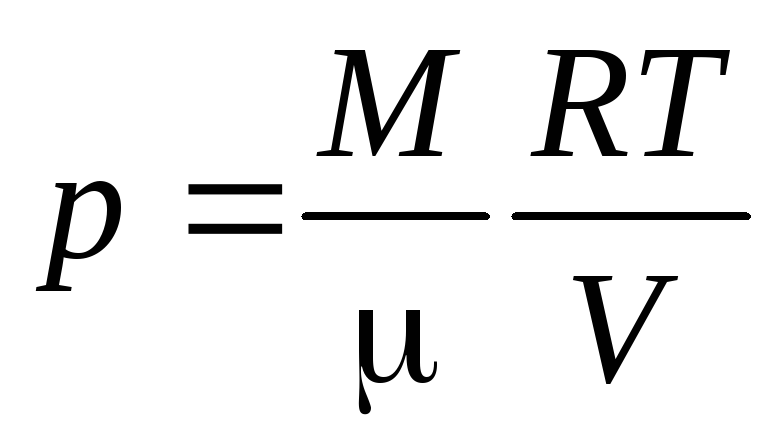(2)
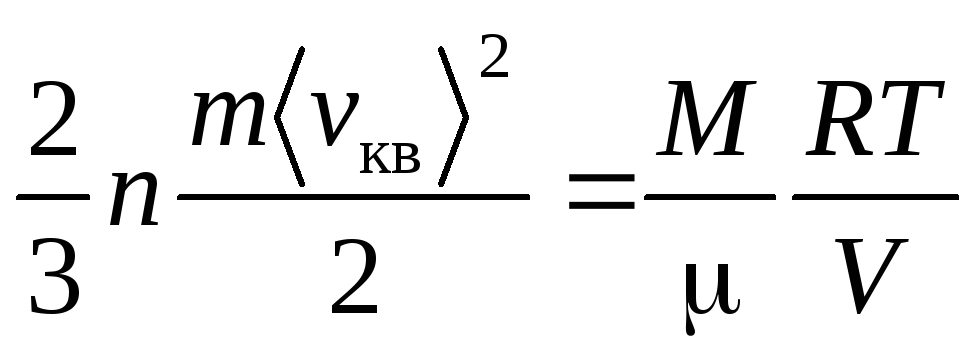
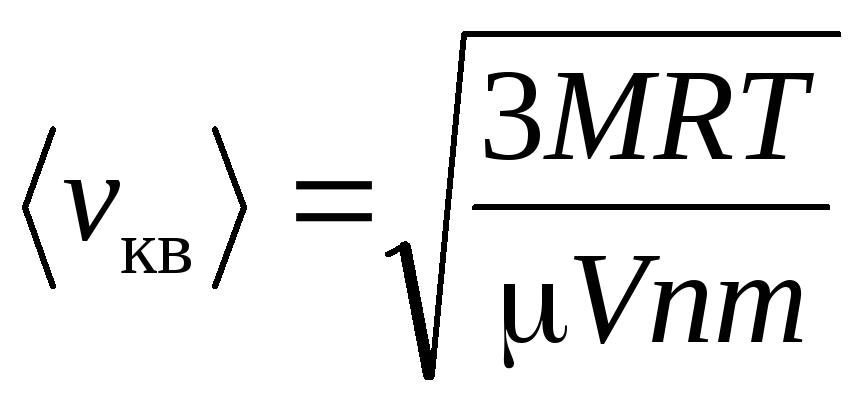
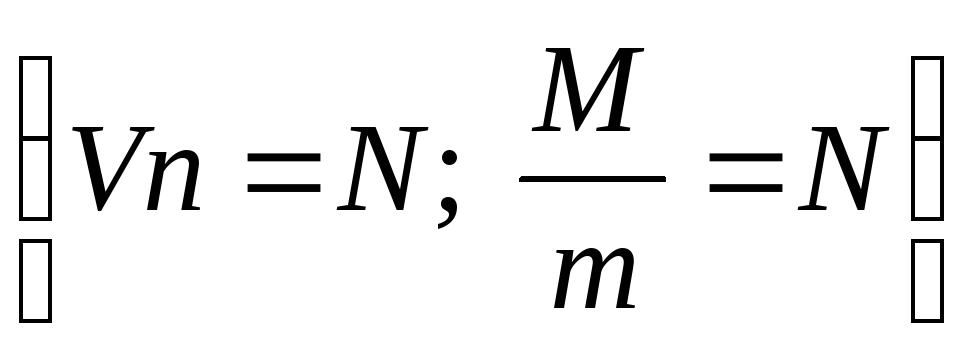
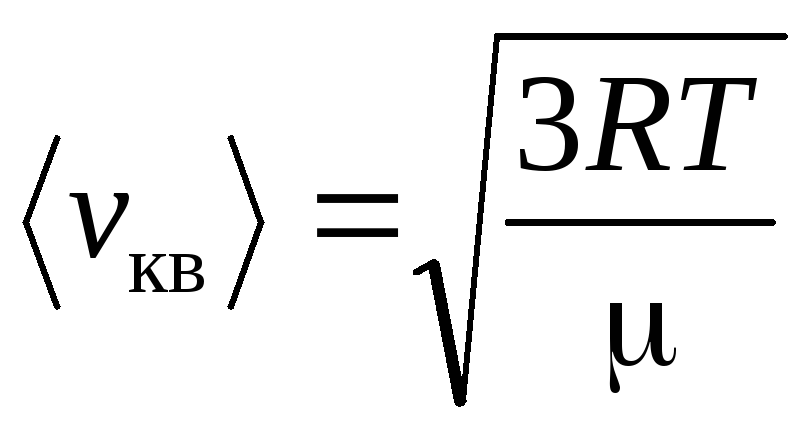, (3)
т.е. средняя
квадратичная скорость пропорциональна
корню квадратному от абсолютной
температуры газа
.
Закон Максвелла
описывается функцией f
(v
),
называемойфункцией распределения
молекул по скоростям
.
Если
разбить диапазон скоростей молекул на
малые интервалы, равные dv
, то на
каждый интервал скорости будет приходиться
некоторое число молекул dN
(v
),
имеющих скорость, заключенную в этом
интервале. Функцияf
(v
) определяет
относительное число молекул dN
(v
)/N,
скорости которых лежат в интервале отv
доv+
dv
, т.е.
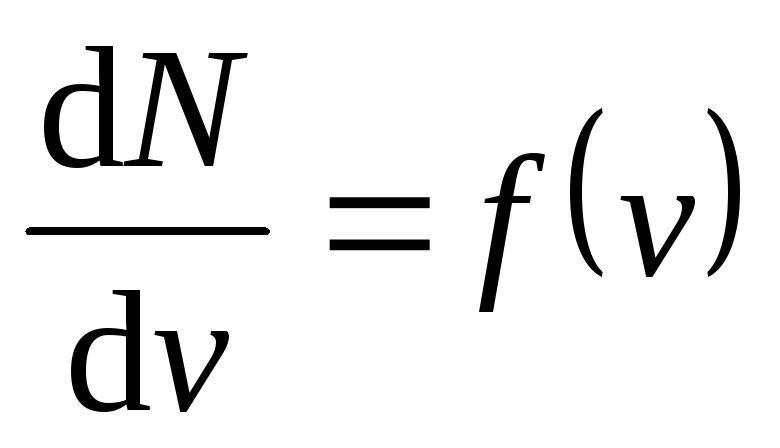максвелловская
функция распределения по скоростям
,
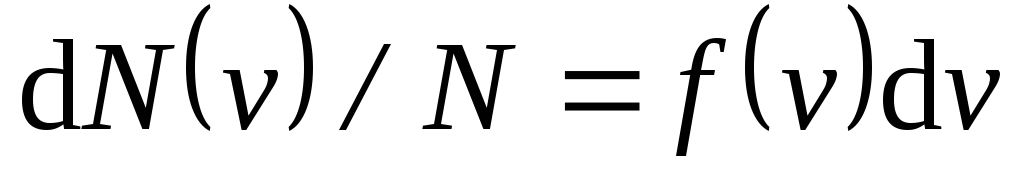откуда
.
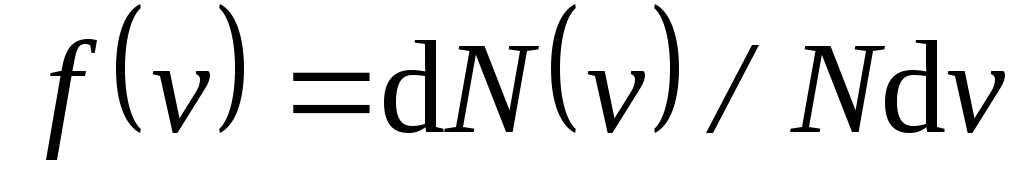Применяя методы
теории вероятностей, Максвелл нашел
функцию f
(v
) –закон для
распределения молекул идеального газа
по скоростям:
.
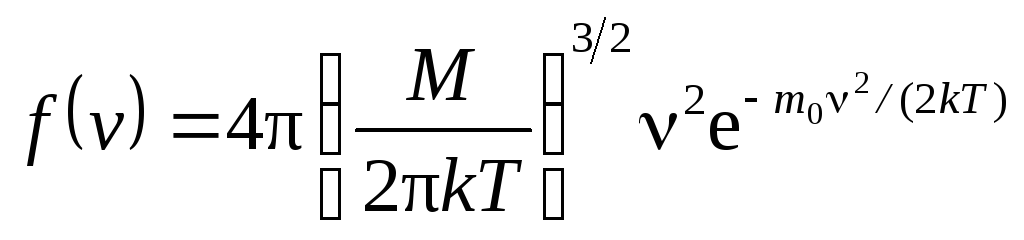(4)
N
v
/N
v
v+
v
S
f
v
.
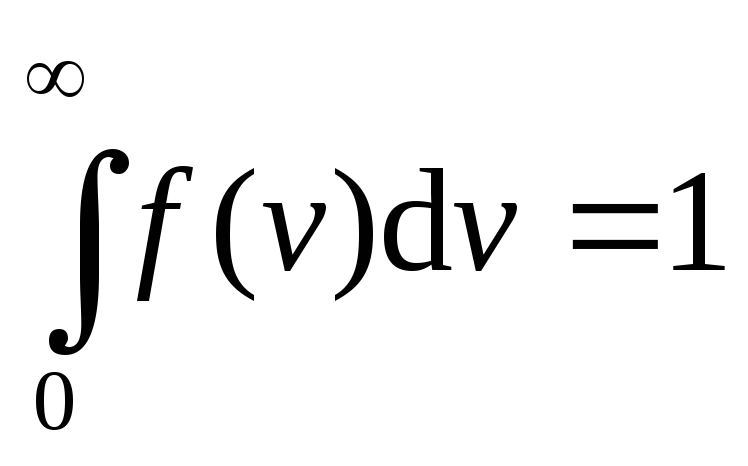(5)
Наиболее вероятной
скоростью
v
в называется
скорость, вблизи которой на единичный
интервал скорости приходится наибольшее
число молекул.
Средняя скорость
молекулы
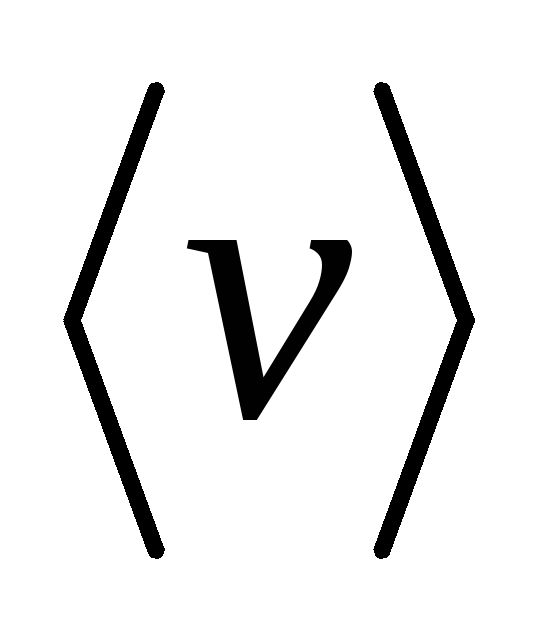(средняя арифметическая скорость):
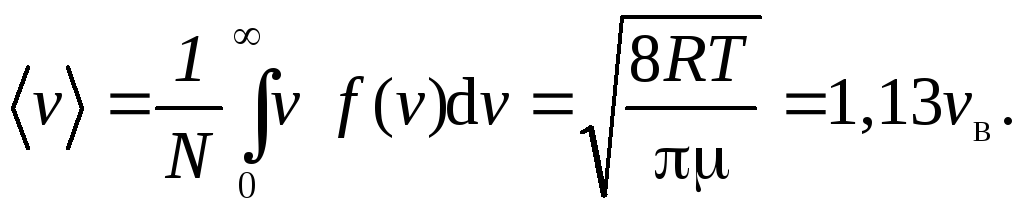(7)
Средняя квадратичная
скорость
(8)
Из формулы (6)
следует, что при повышении температуры
максимум функции распределения
молекул по скоростям смещается
вправо (значение наиболее вероятной
скорости становится больше). Однако
площадь, ограниченная кривой,
остается неизменной, поэтому при
повышении температуры кривая распределения
молекул по скоростям растягивается и
понижается.
Слайды и текст этой презентации
семяпочки. В 1828 опубликовал «Краткий отчет о наблюдениях в микроскоп…»,
в котором описал открытое им движение броуновских частиц.
Слайд 3Броуновское движение- это тепловое движение взвешенных в жидкости или газе
частиц.
1827 год – наблюдал явление, рассматривая в микроскоп взвешенные в
воде споры плауна. Броуновское движение никогда не прекращается, частицы движутся беспорядочно. Это тепловое движение.
Слайд 6
ПЕРРЕН Жан Батист (1870-1942), французский физик. Экспериментальные исследования Перреном броуновского
что концентрация частиц в поле силы тяжести должна убывать с
высотой по такому же закону, что и концентрация молекул газа.Преимущество — масса броуновских частиц за счёт большой массы происходит быстрее.На основе подсчёта этих частиц на разных высотах определив постоянную Авогадро новым способом.
один из основоположников статистической физики
Максвелл первым высказал утверждение о
статистическом характере законов природы. В 1866 им открыт первый статистический закон — закон распределения молекул по скоростям (Максвелла распределение).
и физической кинетики. Вывел функцию распределения, названную его именем, и
основное кинетическое уравнение газов.
Больцман обобщил закон распределения скоростей молекул в газах, находящихся во внешнем силовом поле, и установил формулу распределения молекул газа по координатам при наличии произвольного потенциального поля (1868-71).
Слайд 10ШТЕРН Отто (1888-1969), физик.
Родился в Германии, с 1933 жил
в США.Отто Штерн измерил (1920) скорость теплового движения молекул газа
(опыт Штерна). Экспериментальное определение скоростей теплового движения молекул газа, осуществленное О. Штерном подтвердил правильность основ кинетической теории газов.
Нобелевская премия, 1943 год.
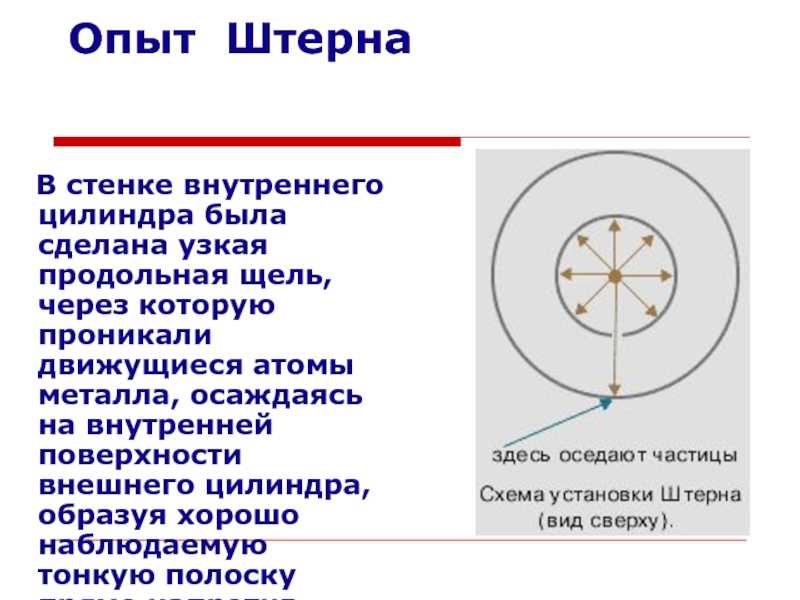
Слайд 11Опыт ШтернаВ стенке внутреннего цилиндра была сделана узкая продольная щель,
через которую проникали движущиеся атомы металла, осаждаясь на внутренней поверхности
внешнего цилиндра, образуя хорошо наблюдаемую тонкую полоску прямо напротив прорези.
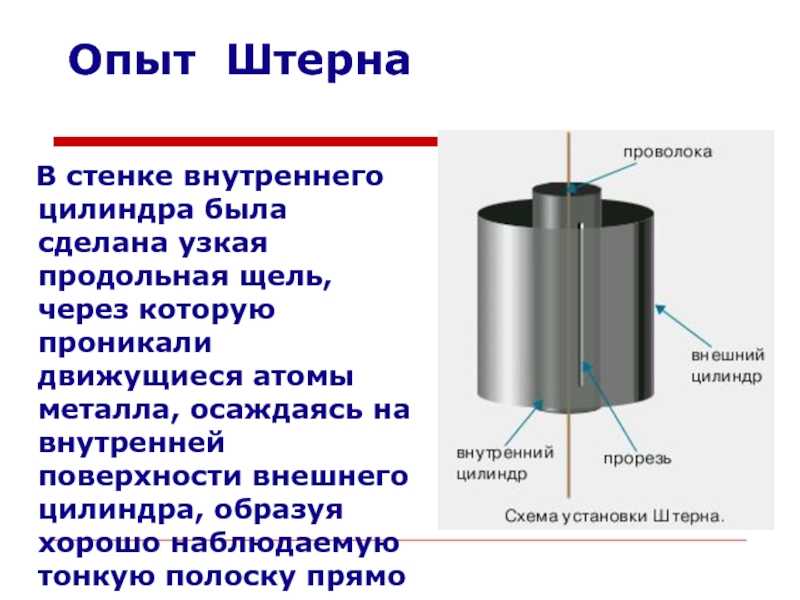
Слайд 12Опыт ШтернаВ стенке внутреннего цилиндра была сделана узкая продольная щель,
через которую проникали движущиеся атомы металла, осаждаясь на внутренней поверхности
внешнего цилиндра, образуя хорошо наблюдаемую тонкую полоску прямо напротив прорези.
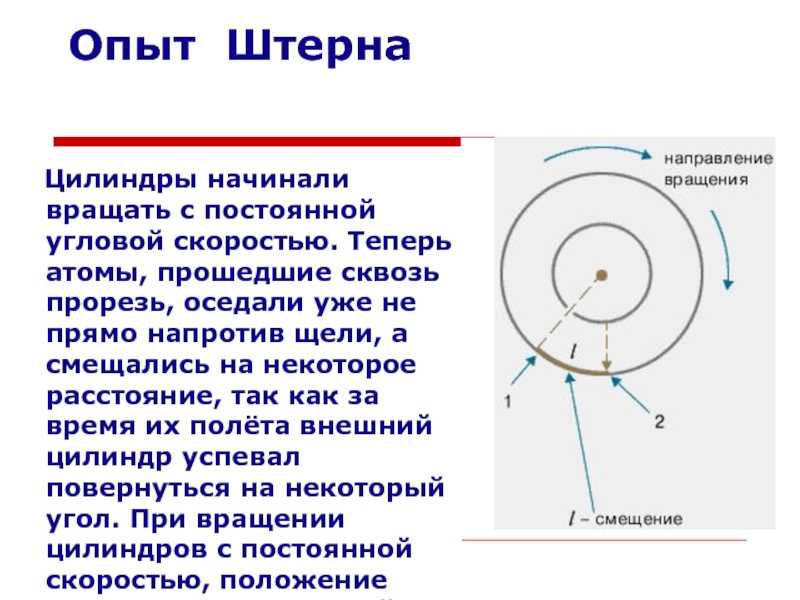
Слайд 13Опыт ШтернаЦилиндры начинали вращать с постоянной угловой скоростью. Теперь атомы,
прошедшие сквозь прорезь, оседали уже не прямо напротив щели, а
смещались на некоторое расстояние, так как за время их полёта внешний цилиндр успевал повернуться на некоторый угол. При вращении цилиндров с постоянной скоростью, положение полоски, образованной атомами на внешнем цилиндре, смещалось на некоторое расстояние.
Слайд 14Опыт ШтернаЗная величины радиусов цилиндров, скорость их вращения и величину
смещения легко найти скорость движения атомов. Время полета атома t
от прорези до стенки внешнего цилиндра можно найти, разделив путь, пройденный атомом и равный разности радиусов цилиндров, на скорость атома v. За это время цилиндры повернулись на угол φ, величину которого найдем, умножив угловую скорость ω на время t. Зная величину угла поворота и радиус внешнего цилиндра R2, легко найти величину смещения L и получить выражение, из которого можно выразить скорость движения атома
Слайд 15Опыт
Штерна
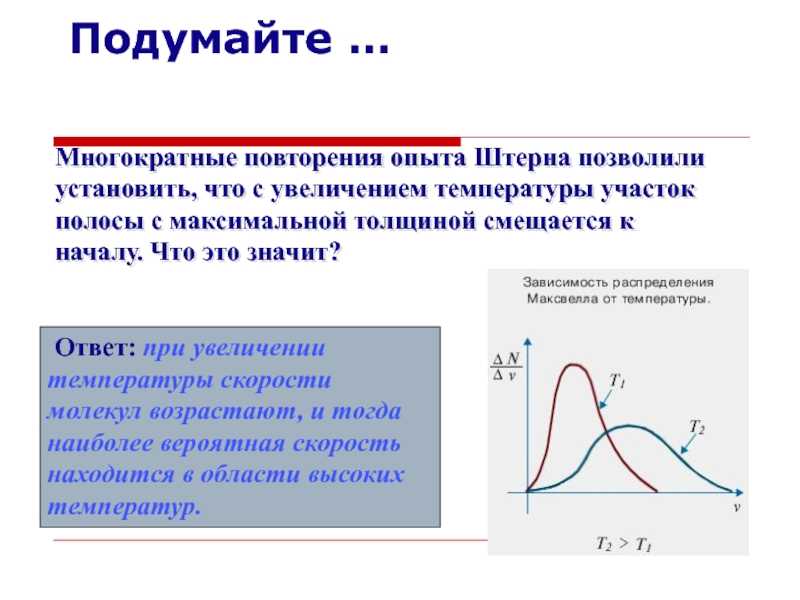
показало, что полоска оказалась размытой и неодинаковой по толщине. Как
можно объяснить этот факт?
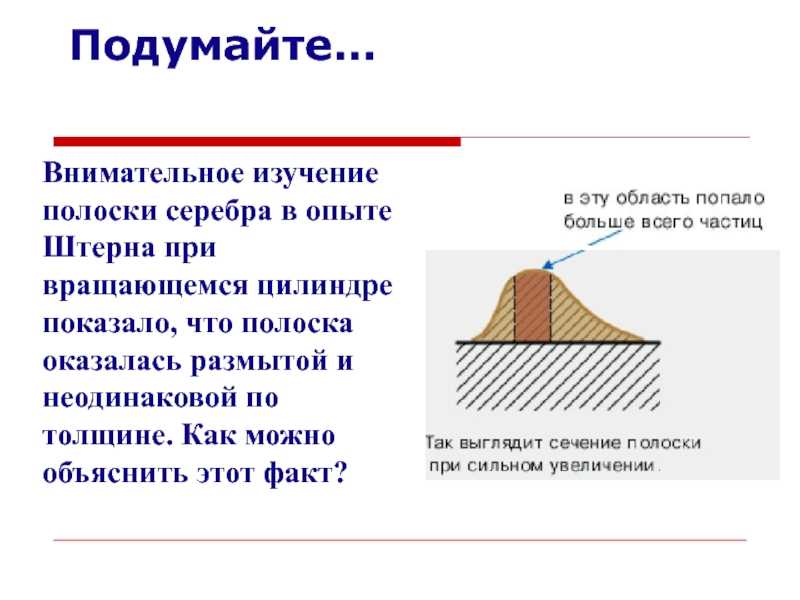
температуры участок полосы с максимальной толщиной смещается к началу. Что
это значит?
Ответ: при увеличении температуры скорости молекул возрастают, и тогда наиболее вероятная скорость находится в области высоких температур.
