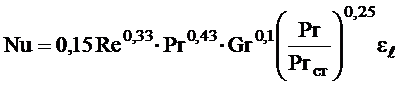Уравнение ньютона рихмана теплоотдача через плоскую стенку

Уравнение ньютона рихмана коэффициент теплоотдачи

1. Конвективный перенос теплоты

Конвекция возможна только в текучей среде, в которой перенос теплоты связан с переносом самой среды. Конвекция теплоты всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно происходит соприкосновение отдельных частиц, имеющих различные температуры. Совместный перенос теплоты путем конвекции и теплопроводности называют конвективным теплообменом.

Теплоотдача — конвективный теплообмен между движущейся средой и поверхностью (стенкой).

Количество теплоты, переданное в процессе теплоотдачи, определяется по уравнению Ньютона-Рихмана:

для установившегося режима

, Вт; (1.1)

для неустановившегося режима

, Дж, (1.2)

где α — коэффициент теплоотдачи, Вт/(м 2 ∙К); t _ж , t _ст – средние температуры жидкости и стенки, °С; F – поверхность стенки, м 2 ; Q ( Q / ) – тепловой поток (количество теплоты), Вт (Дж); τ – время, с.

Коэффициент теплоотдачи α – характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Коэффициент α показывает, какое количество тепла передается от единицы поверхности стенки к жидкости в единицу времени при разности температур между стенкой и жидкостью в 1 градус (К), .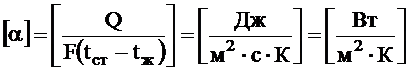

Установлено, что коэффициент теплоотдачи зависит от многих факторов: вида и режима движения жидкости, ее физических свойств, размеров и формы стенки, шероховатости стенки. Определение α является основной задачей расчета теплообменных аппаратов. Обычно коэффициент теплоотдачи определяют из критериальных уравнений, полученных преобразованием дифференциальных уравнений гидродинамики и конвективного теплообмена методами теории подобия.

Согласно положений теории подобия конвективный теплообмен без изменения агрегатного состояния вещества в стационарных условиях может быть описан критериальным уравнением вида:

, (1.3)

— критерий Нуссельта, характеризующий подобие процессов теплопереноса на границе между стенкой и потоком жидкости;

— критерий Рейнольдса, который характеризует гидродинамический режим потока при вынужденном движении и является мерой соотношения сил инерции и вязкого трения;

— критерий Прандтля, который характеризует физико – химические свойства теплоносителя и является мерой подобия температурных и скоростных полей в потоке;

— критерий Грасгофа, характеризующий соотношение сил вязкого трения и подъемной силы, описывает режим свободного движения теплоносителя;

— безразмерный геометрический симплекс, характеризующий геометрическое подобие системы.

В выражении этих критериев: — кинематический коэффициент вязкости теплоносителя, м 2 /с; w — скорость движения теплоносителя, м/с; – коэффициент температуропроводности, м 2 /с; g – ускорение свободного падения м/с 2 ; l – определяющий размер, м; — характерный размер, м; β – коэффициент температурного расширения, 1/К; ρ – плотность теплоносителя, кг/м 3 ; ∆ t = t _ст — t _ж – температурный напор между стенкой и теплоносителем, 0 С; λ – коэффициент теплопроводности теплоносителя, Вт/(м·К); μ – динамический коэффициент вязкости, Па·с; с – теплоемкость теплоносителя, Дж/(кг·К); τ – время процесса, с.

Критерий Нуссельта, входящий в уравнение (1.3), является определяемым. При известном значении Nu коэффициент теплоотдачи может быть рассчитан по формуле:

. (1.4)

Для расчета числа критерия Нуссельта при вынужденном движении потока в прямых трубах или каналах можно рекомендовать следующие уравнения:

а) для ламинарного режима движения теплоносителя, :

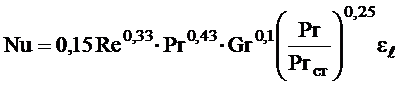, (1.5)

где — критерий Прандтля для теплоносителя при температуре стенки;

б) для переходного режима движения теплоносителя, :

. (1.6)

Значение коэффициента С определяется из таблицы 1.1 в зависимости от величины критерия Рейнольдса.

Для приближенных расчетов можно пользоваться уравнением:

. (1.7)

Коэффициент теплоотдачи

Коэффициент пропорциональности \displaystyle{ \alpha } — коэффициент теплоотдачи — плотность теплового потока при перепаде температур на 1 K, измеряется в Вт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.

\displaystyle{ \alpha } — количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:

• от вида теплоносителя и его температуры;
• от температуры напора, вида конвекции и режима течения;
• от состояния поверхности и направления обтекания;
• от геометрии тела.

Поэтому \displaystyle{ \alpha } — функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.

Эквивалентная запись:

\displaystyle{ \frac{d}{dt}\frac{\partial}{\partial S}Q=\alpha\Delta T. }

Из вышеприведённой дифференциальной формулировки можно вывести интегральную:

Закон Ньютона служит одним из видов граничных условий (синоним — «условия третьего рода»), которые ставятся в задачах теплопроводности. В этом случае он записывается так (учтён также закон Фурье):

\displaystyle{ \frac{\partial T}{\partial n}=k(T_\mathrm{out}-T_\mathrm{in}). }

Заметим, что данный закон описывает ситуацию только на границе тела, внутри же температура определяется температуропроводностью тела. Тепловой поток внутри тела определяется по закону Фурье, что позволяет найти распределение, решив уравнение теплопроводности.

Если внутренняя теплопроводность намного больше, чем коэффициент теплоотдачи (иначе: маленькое число Био), то внутри устанавливается почти однородная температура (если на всей поверхности также она одинакова) и тогда можно записать уравнение охлаждения тела в виде:

\displaystyle{ \frac{\partial T}{\partial t}=k(T_\mathrm{out}-T). }

Здесь коэффициент \displaystyle{ k=\frac{\alpha S}{C} }, где \displaystyle{ C } — теплоёмкость тела.

Из этого уравнения несложно получить, что температура тела в такой ситуации будет приближаться по экспоненте к температуре окружающей среды \displaystyle{ T_\mathrm{out} }:

\displaystyle{ T(t)=T_\mathrm{out}+e^{-kt}(T_0-T_\mathrm{out}). }