Примеры решения задач
Задача 1
Вычислить суммарную амплитуду плоской монохроматической дифрагированной волны на щели, плоскость которой перпендикулярна распространению волны, при условии, что экран расположен далеко от щели.
Решение
Так как экран далеко, можно считать, что для участка щели с координатой у расстояние до точки наблюдения равно \(у\;\times\;\sin\left(\psi\right).\)
Если мысленно разбить щель на одинаковые участки шириной \(dy\), одинаковые по модулю комплексные амплитуды от соседних участков в точке наблюдения будут развернуты друг относительно друга на одинаковые углы \(\frac{2\mathrm\pi}\lambda\;\times\;dу\;\times\;\sin\left(\psi\right)\).
Изменение угла psi между нормалью к плоскости щели и направлением наблюдения приведет к изменению угла d\varphi между векторами комплексных амплитуд волн, пришедших от соседних участков щели.
Чтобы найти суммарную амплитуду, нужно сложить комплексные числа с одинаковыми амплитудами и разными фазами \(\frac{2\mathrm\pi}\lambda\;\times\;у\;\times\;\sin\left(\psi\right).\)
Ответ: суммарную амплитуду можно вычислить по формуле:
\(E’ = \int_{0}^{d} E_{0}\times exp \times dy\)
Задача 2
Квадратное отверстие со стороной 0,2 см освещено параллельным пучком нормально падающих лучей света.
Найти размер изображения отверстия на экране, параллельном отверстию и удаленном от него на 50 метров. За границу изображения на экране принять положение дифракционного максимума первого порядка для наиболее отклоняемых лучей (видимый спектр от 400 до 700 нм).
Решение
Напряженность электрического поля волны в данных условиях можно вычислить с помощью формулы:
\(E(х,у)=\frac{Е_{0}}{b^{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-\frac{ikxx’}{l})dx’\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-\frac{ikyy’}{l})dy’\)
Введем углы дифракции \(\vartheta_1\) и \(\vartheta_2\):
\(\tan\left(\vartheta_1\right)\;=\;\frac хl\)
\(\tan\left(\vartheta_2\right)\;=\;\frac yl\)
Так как расстояние l достаточно велико, углы дифракции малы, соответственно, есть основания предполагать, что их тангенс примерно равен синусу. Тогда формула напряженности поля с подставленными значениями будет выглядеть так:
\(E(х,у)=\frac{Е_{0}}{b^{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-ikx’\sin\vartheta_1)dx’\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-iky’\sin\vartheta_2)dy’\)
Интегрировав выражение, получим:
\(E=Е_0sinc\left(\frac{kb\sin\left(\vartheta_1\right)}2\right)sinc\left(\frac{kb\sin\left(\vartheta_2\right)}2\right)\)
Угловое выражение дифракционных максимумов первого порядка:
\(\frac{kb\sin\left(\vartheta\right)}2\;=\;\frac{3\mathrm\pi}2\)
\(\sin\left(\vartheta\right)\;=\;\frac{3\mathrm\lambda}{2b}\)
Вычислим линейное расстояние D между оптической осью системы и дифракционным максимумом:
\(D\;=\;l\sin\left(\vartheta\right)\;=\;\frac{3\mathrm{λl}}{2b}\)
Подставим в выражение максимальную длину волны видимого света, 700 нм.
Метод зон Френеля, основные принципы работы
Опредление
С целью упрощения решений задач волновая поверхность S разбивается на отдельные зоны. Данный способ называют методом зон Френеля.
Точки поверхности S, которые являются границей первой или центральной зоны и удалены от точки М на расстояние:
\(l+\frac{\lambda }{2}\)
Точки сферы S, которые находятся на расстоянии:
\(l+\frac{2\lambda }{2}\)
\(l+\frac{3\lambda }{2}\)
и так далее относительно точки М, образуют 2, 3 и так далее зоны Френеля.
В точке М образуются колебания. Они расположены между двумя соседними зонами, фазы которых противоположны по причине разности ходя от этих зон до точки М:
\(\Delta =\frac{\lambda }{2}\)
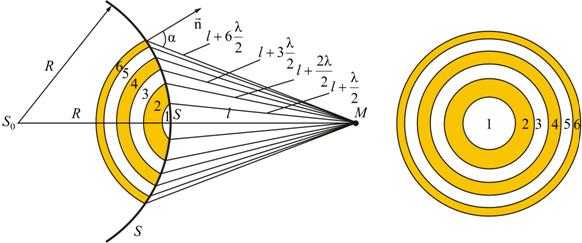
В процессе сложения колебания друг друга ослабляют:
\(A=A_{1}-A_{2}+A_{3}-A_{4}+…+A_{i}\)
Где A является амплитудой результирующего колебания, Аi представляет собой амплитуду колебаний, возбуждаемую i-й зоной Френеля.
Значение Аi определяется площадью Si зоны и углом αi между нормалью к поверхности и прямой, направленной в точку M. Расчет площади одной зоны выглядит следующим образом:
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\Delta S_{i}=S_{i}-S_{i-1}=\frac{\pi Rl\lambda }{R+l}\left(i-i+1 \right)=\frac{\pi Rl\lambda }{R+l}\)
Исходя из представленного уравнения, можно сделать вывод о независимости площади зоны Френеля от номера зоны i. Данное утверждение позволяет сделать вывод о том, что при малых числах i соседние зоны будут обладать одинаковыми площадями. В то время, как номер зоны увеличивается, возрастает угол αi, а также снижается интенсивность излучения зоны по направлению к точке М, то есть уменьшается амплитуда Аi. Другой причиной данного явления служит увеличение расстояния до точки М:\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)В целом количество зон Френеля, которые уменьшаются на части сферы, направленной к точке М, достаточно большое:
если радиус R=l=1 метр,
\(\lambda =-5\times 10^{-7}\) составляет 500 нм.
Количество зон \(N\approx 3\times 10^{5}\)
Радиус первой зоны \(r_{1}\approx 0.16\) мм
Исходя из вышеизложенной информации, можно сделать вывод о равенстве углов соседних зон между нормалью к зоне и направлением на точку М. Таким образом, наблюдается примерное равенство амплитуд волн, которые приходят в точку М от соседних волн. При прямолинейном распространении световой волны фазы колебаний, которые образованы в соседних зонах, будут отличаться на π. Согласно этим данным, в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны рассчитывается, как среднее арифметическое от амплитуд зон, которые к ней примыкают:
\(A_{m}=\frac{A_{m-1}+A_{m+1}}{2}\)
В таком случае, исходное уравнение можно преобразовать следующим образом:
\(A=\frac{A_{1}}{2}+\left(\frac{A_{1}}{2}-A_{2}+\frac{A_{3}}{2} \right)+\left(\frac{A_{3}}{2}-A_{4}+\frac{A_{5}}{2}\right)+…=\frac{A_{1}}{2}\)
Из равенства площадей, которыми обладают соседние зоны, вытекает нулевое значение выражения, заключенного в скобках. Тогда результирующая амплитуда будет равна:
\(A=\frac{A_{1}}{2}\)
Расчет интенсивности излучения имеет вид:
\(J\sim A^{2}\)
Таким образом, результирующая амплитуда, которая образована в какой-либо точке М всей сферической поверхностью, определяется, как половина амплитуды, сформированной одной лишь центральной областью, а интенсивность составляет:
\(J=\frac{J_{1}}{4}\)
Радиус, которым характеризуется центральная зона, небольшой:
\(r_{1}\approx 0.16\) мм
Тогда допустимо считать распространение света от точки Р до точки М прямолинейным. В условиях, когда путь волны преграждает непрозрачный экран, в котором есть отверстие, открывающее только центральную зону Френеля, то амплитуда в точке М составляет А1. Поэтому, интенсивность в точке М превышает в 4 раза тот же показатель, но в условиях без экрана. В случае, когда все зоны с четными номерами закрыты, интенсивность света будет увеличиваться.
Таким образом, объясняют прямолинейность распространения света в условиях однородной среды с помощью принципа Гюйгенса-Френеля. Справедливость деления волнового фронта на зоны Френеля нашла подтверждение в ходе эксперимента. Для опыта используют зонные пластинки, представляющие собой систему чередующихся прозрачных и непрозрачных колец. Эксперимент подтверждает возможность увеличения освещенности в точке М с помощью зонных пластинок по принципу собирающей линзы.
Принцип Гюйгенса-Френеля
Опредление
Дифракцией света в наиболее распространенном понятии называют огибание световыми лучами границы непрозрачных тел или экранов, то есть проникновение света в область с геометрической тенью.
Максимально рельефно дифракцию света можно наблюдать в зонах с резким изменением плотности потока лучей:
- около каустик;
- вблизи фокуса линзы;
- у границ геометрической тени.
Дифракция волн тесно связана с процессами, при которых волны распространяются и рассеиваются в неоднородных средах.
Определение
Дифракция — это комплекс явлений, которые можно наблюдать в процессе распространения света в среде, отличающейся резкими неоднородностями, габариты которых соотносимы с длиной волны и связаны с отклонениями от законов геометрической оптики.
Огибание препятствий звуковыми волнами, то есть дифракцию звуковых волн, можно заметить в повседневной жизни.
Пример
К примеру, за углом дома слышен звук. Для того чтобы наблюдать дифракцию световых лучей, требуются специальные условия, что является причиной небольшой длины световых волн. Интерференция не отличается существенно от дифракции. Данные явления зависят от перераспределения светового потока в результате суперпозиции волн.
Определение
Дифракция объясняется принципом Гюйгенса. Согласно данному утверждению, каждая точка, которую достигает волна, является центром вторичных волн, а огибающая этих волн определяет положение волнового фронта в следующий момент времени.
На рисунке изображен непрозрачный экран, на отверстие в котором нормально падает плоская волна.
Каждая точка области волнового фронта, выделенного отверстием, представляет собой источник вторичных волн. В условиях однородной среды они будут иметь сферическую форму. С помощью огибающих вторичных волн для некоторого момента времени можно увидеть, что фронт волны достигает области геометрической тени, то есть волна огибает края отверстия.
Благодаря принципу Гюйгенса, можно решить задачу, связанную с направлением, в котором распространяется волновой фронт. Но утверждение не касается вопроса о таких характеристиках разнонаправленных волн, как амплитуда и интенсивность. Решающая роль в определении волновой природы света отведена О. Френелю, который проводил данные исследования в начале XIX века. Ученый представил объяснение явлению дифракции и ее количественный расчет. В 1818 году Френель был удостоен премии Парижской академии за достижения в данной области.
Френель дополнил принцип Гюйгенса физическим смыслом с помощью идеи интерференции вторичных волн. Ученый рассматривал дифракцию по средствам нескольких ключевых положений, которые не требую доказательств. Комплекс данных утверждений называют принципом Гюйгенса-Френеля. Исходя из принципа Гюйгенса, каждая точка фронта волны рассматривается в качестве источника вторичных волн. Френель значительно развил это утверждение:
- Все вторичные источники фронта волны, которая исходит из одного источника, когерентны между собой.
- Участки волновой поверхности с разными площадями испускают равные интенсивности или мощности.
- Для каждого вторичного источника характерно излучение света в большей степени по направлению к внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при \(\alpha \geq \frac{\pi }{2}\)
- Вторичные источники характеризуются принципом суперпозиции, то есть излучение одних областей волновой поверхности не оказывает влияние на излучение других участков. Это можно понять, когда часть волновой поверхности прикрыта непрозрачным экраном, а вторичные волны излучаются открытыми областями так, как если бы экран отсутствовал.
Принцип Гюйгенса
Работу подобного явления описал Христиан Гюйгенс. После определённого количества проведённых экспериментов со световыми волнами на водной поверхности, он предложил науке новое объяснение такого феномена и дал ему название волновой фронт. Таким образом, Христиан дал возможность понять, как будет вести себя луч света при попадании на какую-то поверхность другого типа.
Его принцип звучит следующим образом:
Точки поверхности, заметные в определённый момент времени, могут быть причиной для вторичных элементов. Площадь, которая прикасается ко всем вторичным волнам, считается волновой сферой в последующие отрезки времени.
Он объяснил, что все элементы следует рассматривать как начало сферических волн, которые имеют название как вторичные волны. Христиан заметил, что волновой фронт по своей сути является совокупностью этих точек касания, отсюда и выплывает весь его принцип. Кроме этого, вторичные элементы представляются сферической формы.
Стоит запомнить, что волновой фронт — это точки геометрического смысла, до которых доходят колебания к определённому моменту времени.
Вторичные элементы Гюйгенса представляются не как настоящие волны, а лишь дополнительные, имеющие форму сферы, используемые не для расчёта, а лишь приблизительного построения. Поэтому эти сферы вторичных элементов по своей сути имеют только огибающее действие, что позволяет образовываться новому волновому фронту. Этот принцип хорошо объясняет работу дифракции света, однако решает вопрос только направления фронта, а не объясняет, откуда появляется амплитуда, интенсивность волн, распыление волн и их обратное действие. Френель использовал принцип Гюйгенса для устранения этих недостатков и дополнения его работы физическим смыслом. Через некоторое время учёный представил свою работу, которая полностью подержалась научным сообществом.
Решение уравнения по принципу
Интегральная формулировка принципа
Формулировка через интеграл по траекториям — это способ найти множество траекторий вторичных волн. Этот способ на основе принципа Гюйгенса-Френеля был адаптирован для расчета бесконечного множества траекторий квантовой амплитуды.
Сущность метода заключается в делении поверхности на столь малые части, чтобы их можно было принять за материальные точки, и последующем суммировании величин по всем участкам изменения конкретной величины. Волновой фронт, расходящийся от точечного источника, имеет вид сферы.
На схеме мы видим точку наблюдения Р, относительно которой определяем комплексную амплитуду поля, обусловленную действием вторичного источника на участке \(ds\), по формуле:
\(K(\alpha)\;\frac{f_0\left(\overrightarrow{r_1}\right)ds}{\lambda r}exp\;(ikr)\)
где \(f_0\left(\overrightarrow{r_1}\right)\) — комплексная амплитуда поля первичной волны на участке ds;
\(K(\alpha)\) — коэффициент наклона;
\(\lambda\) — длина волны.
Когда в задаче идет речь о дифракции, нужно применить постулат о граничных условиях и проинтегрировать вышеприведенное выражение по поверхности S, разделяя затененные и не прикрытые экраном участки.
Определение комплексной амплитуды первичной волны в данном случае выглядит следующим образом:
\(\left\{\begin{array}{l}f_0(\xi,\;\eta)\;-\;в\;области\;отверстия\\0\;-\;на\;затененной\;части\end{array}\right.\)
Тогда комплексную амплитуду в точке наблюдения можно найти по формуле:
\(\int\int_sK(\alpha)\;\frac{f\left(s\right)}{\lambda r}exp\;(ikr)ds\)
В оптических задачах часто используется метод зон Френеля. Он позволяет с помощью геометрических построений определить закономерности распределения интенсивности волн. С целью упрощения расчетов волновую поверхность делят на кольцевые зоны.
Что такое зона Френеля
Определение
Зонами Френеля называют области, на которые можно разделить поверхность световой, либо звуковой волны с целью расчета результатов дифракции света или звука.
Методика анализа была впервые применена О. Френелем в 1815 – 1819 годах. Зону Френеля можно наглядно представить в виде объема радио-волнового канала между двумя передатчиками сигнала.
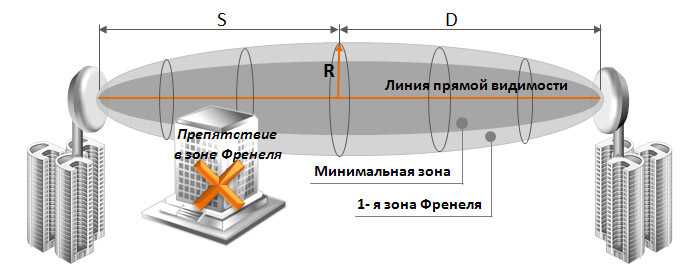
Максимальное значение объема канала отмечено центральной точкой, равноудаленной от двух антенн. Наиболее качественный сигнал обеспечивается путем подбора максимально чистой зоны, в которой отсутствуют физические и радио-волновые препятствия.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Работа Френеля над принципом Гюйгенса
Что он изменил и добавил
Большинство маститых учёных — и среди них Жан Био, Пьер Лаплас, Симеон Пуассон — вслед за Исааком Ньютоном считали свет потоком частиц, или корпускул. В рамках корпускулярной теории были сделаны самые значительные открытия в оптике, например, обнаруженная в 1808 году Этьеном Малюсом поляризация света при отражении.
Волновая теория света не могла объяснить поляризацию и двойное лучепреломление, в то время как у её противников имелись на этот счет хоть и громоздкие, но все же вполне приемлемые гипотезы. В 1815 году Огюстен Френель сопоставил волновую и корпускулярную теории света и, признав преимущества корпускулярной в объяснении прямолинейного распространения света, доказал, что те же явления можно объяснить и в рамках гипотезы колебаний. Через некоторое время, исследуя явления поляризации, Френель понял, что их можно объяснить, только приняв предположение о поперечном характере световых волн. Теоретические рассуждения Гюйгенса о том, как волны огибают препятствия, Френель заменил доказательством интерференции вторичных волн.
Формулировка
Дополнение Френеля к принципу Гюйгенса доказывает, что каждый элемент волнового фронта можно считать центром возбуждения вторичных сферических волн. Световое поле в каждой точке пространства будет определяться их интерференцией.
Расчет радиуса зоны Френеля
С помощью определенных характеристик можно выполнить корректный расчет. Для определения зоны Френеля в ее центре необходимо использовать формулу:
\(Radius (mts.)=17.31\times \sqrt{\frac{D (in km)}{4\times f(in GHz)}}\)
Где D равно расстоянию в километрах, f является частотой в GHz.
Если необходимо рассчитать размер зоны Френеля в любой ее точке, к примеру, в месте, где обнаружено препятствие, следует воспользоваться формулой:
\(r=17.3\sqrt{\frac{1}{f}\frac{D_{1}D_{2}}{D_{1}+D_{2}}}\)
Где f — это частота в GHz, D1 является расстоянием от первой антенны до искомой точки в километрах, D2 равно расстоянию от второй антенны до искомой точки в километрах.
Знание характеристик зоны Френеля позволяет выполнить точные расчеты. В практическом применении представленные формулировки обеспечивают данные для стабильности параметров беспроводного моста и максимально возможной скорости передачи сигнала.
Видео
В интернете можно найти видео, демонстрирующие, как работает принцип Гюйгенса-Френеля. Например, наглядная демонстрация для отражения плоской волны от поверхности доказывает, что угол падения и угол отражения равны.
Если волна падает на плоскость, отражаясь от нее, различные точки волновой поверхности доходят до плоскости неодновременно. Начинают распространяться вторичные колебания.
Касательная к ним — это и есть волновой фронт отраженного колебания. Решив простую геометрическую задачу о равенстве треугольников, можно установить, что углы, под которыми излучение падает и отражается, равны.
Можно построить изображение источника в плоском зеркале. Фронт отраженного возмущения будет сферой с центром в некоторой точке. Эта точка и будет мнимым изображением плоского источника в зеркале.
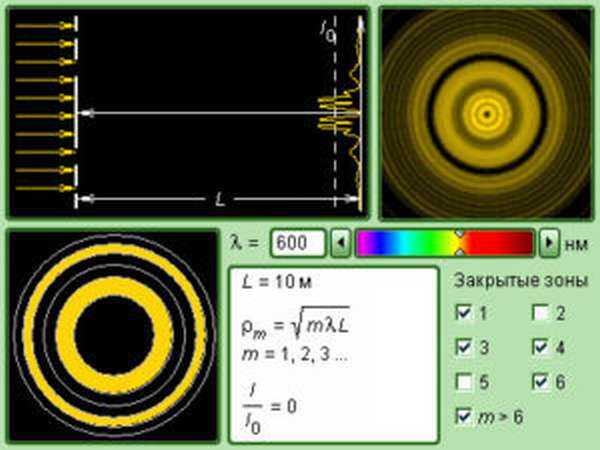
Можно найти видео, иллюстрирующие и другие физические явления. Например, можно пронаблюдать зоны Френеля для электромагнитного колебания. Также можно найти лекции, посвященные принципу Гюйгенса-Френеля и другим вопросам оптики.
Принцип Гюйгенса
Законы геометрической оптики были установлены еще в античности. Однако их полное объяснение в то время было невозможно. Закон отражения света можно было объяснить с механистической позиции по аналогии с упругим ударом шарика о стену. Свету приписывалось корпускулярное строение, и отражение его объяснялось отражением «частиц света» подобно отскоку мяча. Однако закон преломления с механистической точки зрения объяснить было невозможно.
Рис. 1. Законы геометрической оптики.
Лишь во второй половине XVII в. Х. Гюйгенс предложил принцип, который смог объяснить геометрическую оптику. Принцип Гюйгенса гласит, что каждая точка среды, до которой дошла волна, сама становится источником волны. И волновая поверхность в следующий момент времени является огибающей всех этих волн от вторичных источников.
Хотя принцип Гюйгенса впервые был применен именно к свету, этот принцип легче всего понять на механической аналогии, поскольку он не зависит от физической природы волн.
В самом деле, если поглядеть на образование волн на поверхности воды, можно убедиться, что их распространение обусловлено именно тем, что молекулы воды, до которых дошло колебание, сами начинают колебаться и передают колебания соседним молекулам. Говоря простыми словами, препятствия прекращают распространение волн именно потому, что они не дают колеблющимся молекулам воды быть вторичными источниками.
Суть принципа Гюйгенса-Френеля
Это утверждение объясняет и описывает то, как распространяются колебания, например, свет. Оно состоит из двух частей. Первую часть (принцип Гюйгенса) предложил Христиан Гюйгенс в 1678 году. Он предположил, что при распространении излучения из каждой точки волнового фронта начинают исходить новые сферические волны.
Волновой фронт — это поверхность, на которой возмущение находится в одинаковой фазе. Проще говоря, это граница пространства, в котором уже распространилось возмущение. Например, если бросить камень в воду, пойдут круги — волны. Их фронт в этом случае — это самый внешний круг.
Огюстен Жан Френель в 1815 году развил предположение Гюйгенса.
Интерференция — это наложение волн друг на друга. При этом в одних участках колебания они взаимно усиливают друг друга, в других ослабляют. Поэтому для света получается картина из светлых и темных полосок. Пример этого кольца Ньютона, картина из концентрических кругов, получающаяся, если плоско-выпуклую линзу положить на стеклянную пластинку.
Чтобы можно было наблюдать картину интерференции, излучение должно быть когерентным. Это значит, что оно должно иметь постоянную разность фаз и давать колебания такой же частоты, если их сложить.
Утверждение, сделанное Гюйгенсом, помогало определить только направление распространения возмущения и объясняло распространение света, как его описывает геометрическая оптика. Дополнение принципа Гюйгенса позволяет рассчитывать амплитуду и интенсивность.