Вектор и скаляр отличие

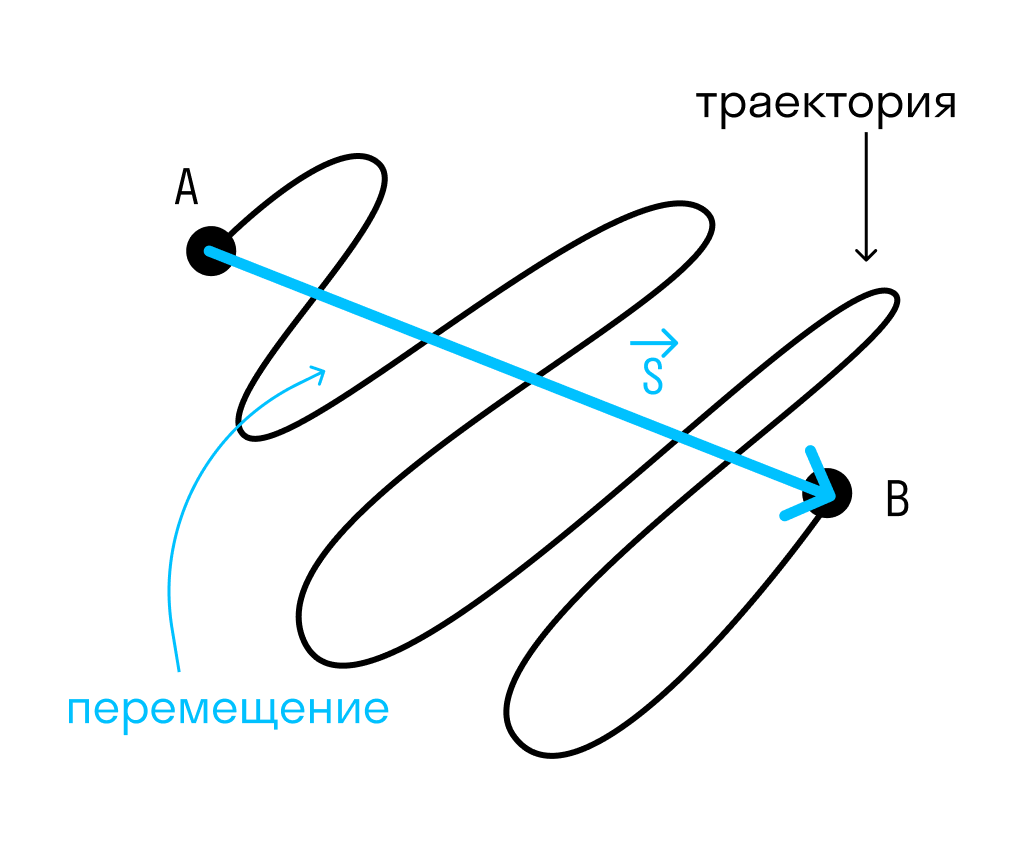
Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки

Очень важно разделить движение по окружности и вращение тела

При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.

При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.

Центростремительное ускорение

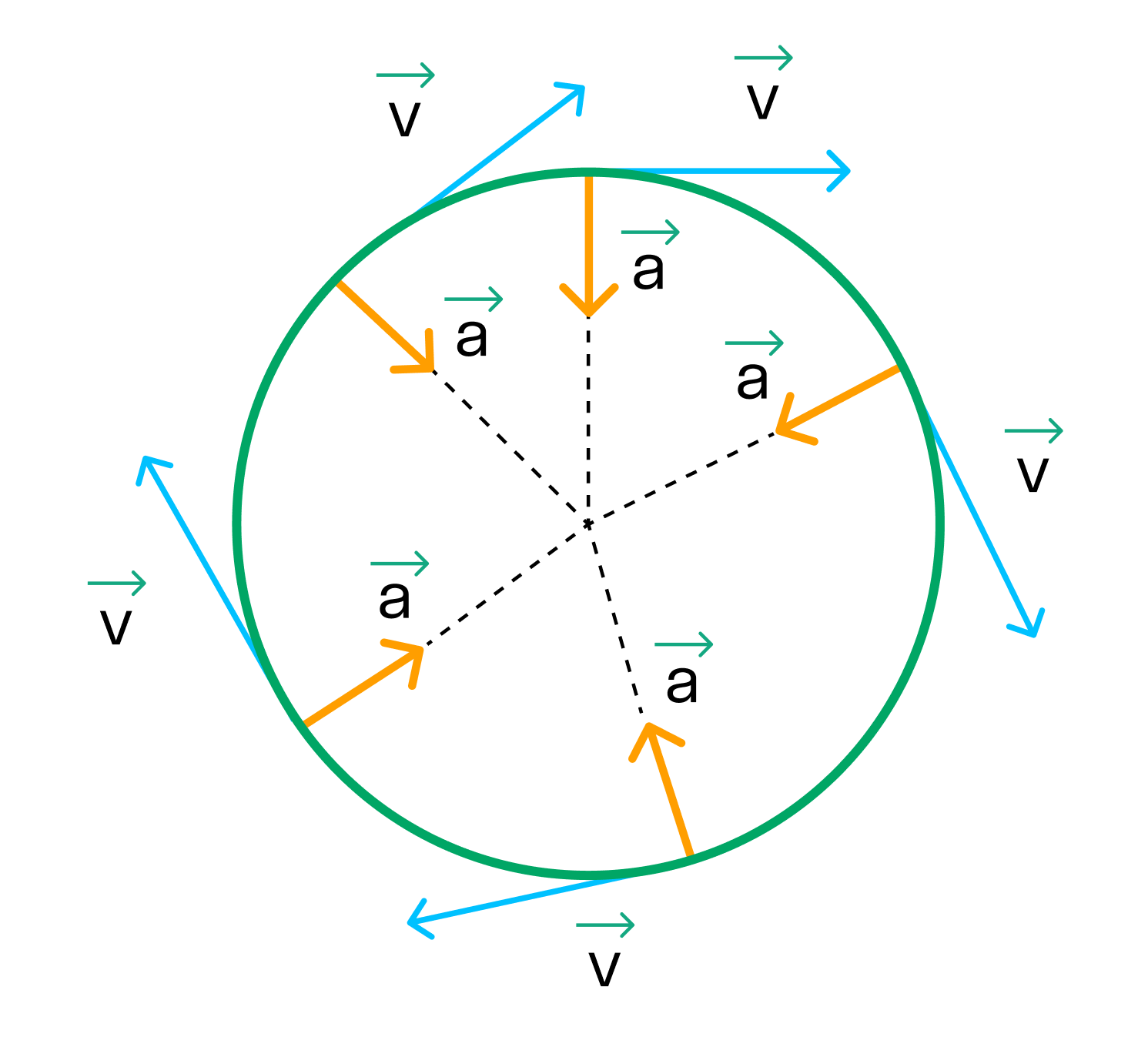
При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.

Центростремительное ускорение aц = v2/R aц — центростремительное ускорение [м/с2] v — скорость [м/с] R — радиус окружности

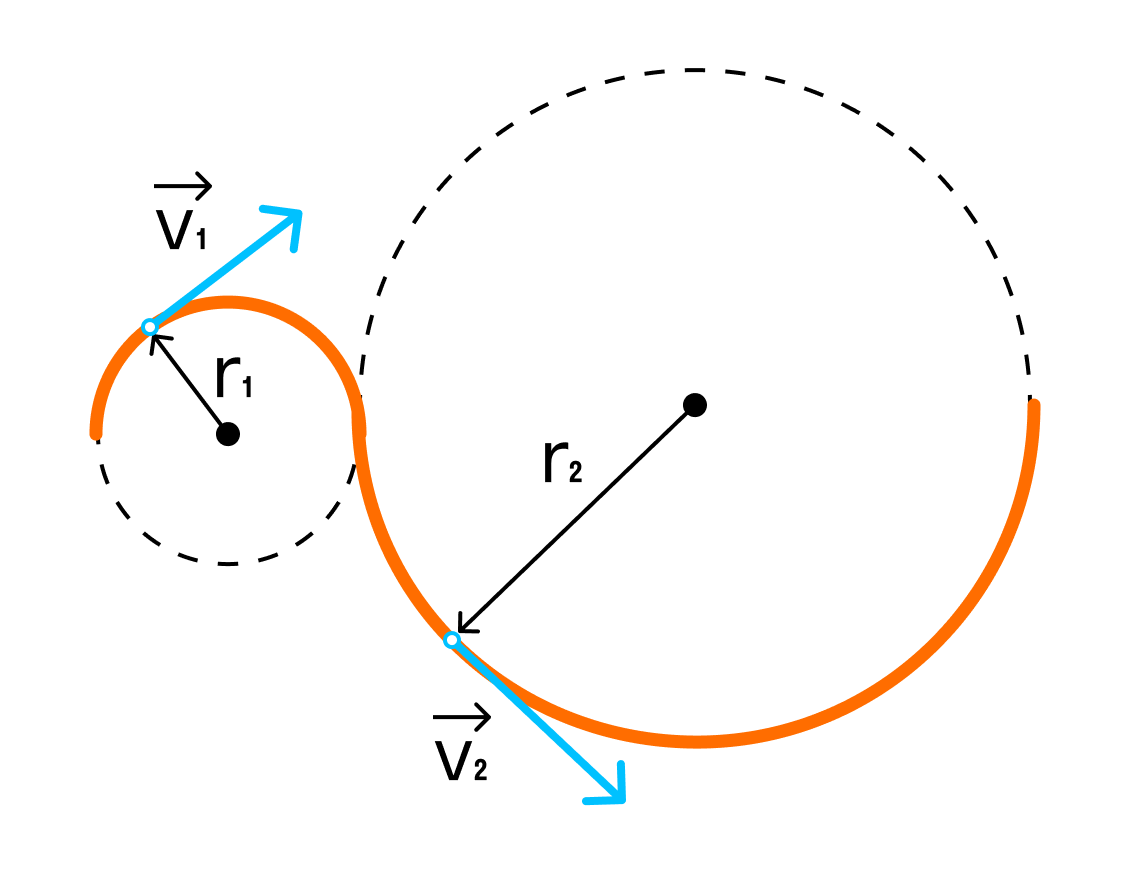
Задачка

Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?

Решение:

Возьмем формулу центростремительного ускорения тела

a_ц = v2/R

В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.

36 км/с = 10 м/с

Теперь можно подставить значения в формулу:

a_ц = 102/120 = 100/120 = 10/12 ≃ 0,83 м/с2

Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с2

Эту и другие темы мы разбираем на курсе физики за 9 класс.

Как изображать

Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

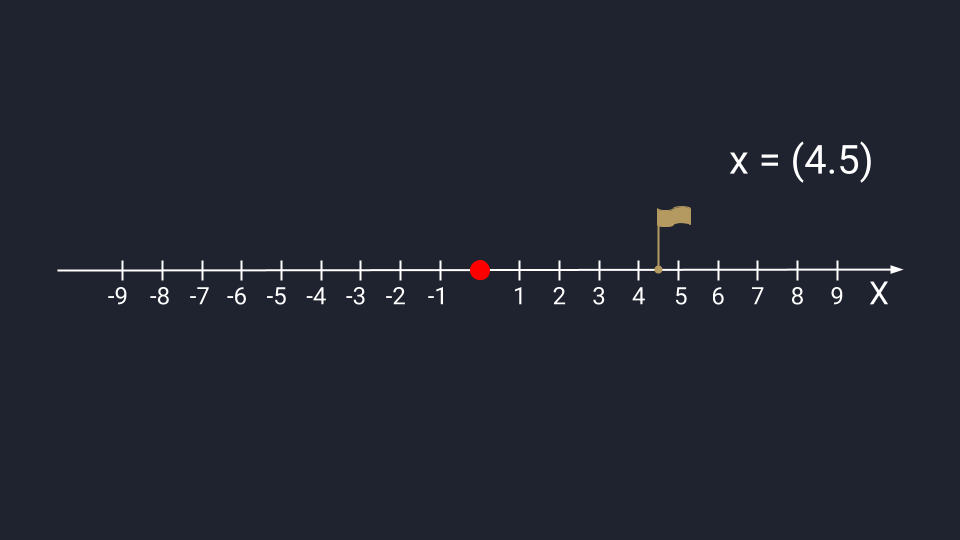Графическое представление скаляра. Записывается в круглых скобках

Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

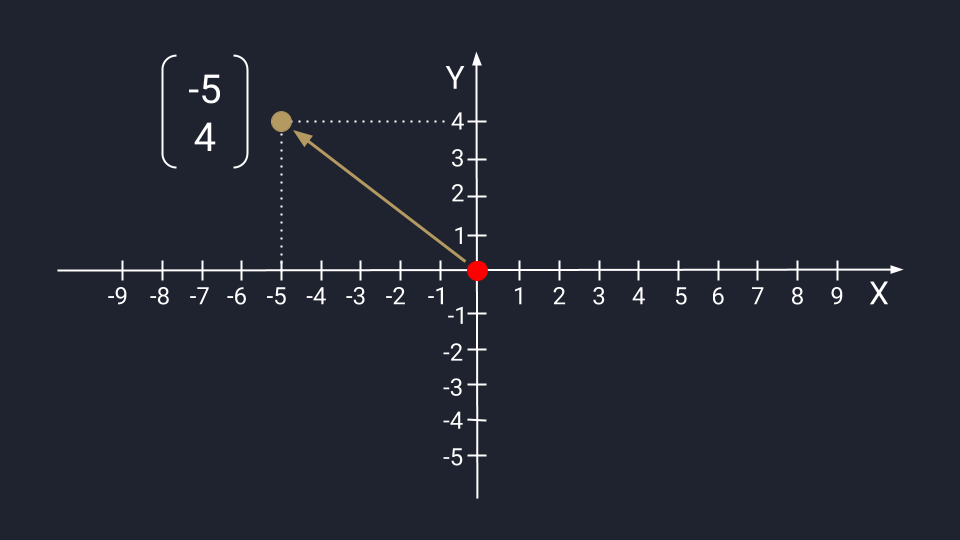Графическое представление числового вектора в двух измерениях

Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

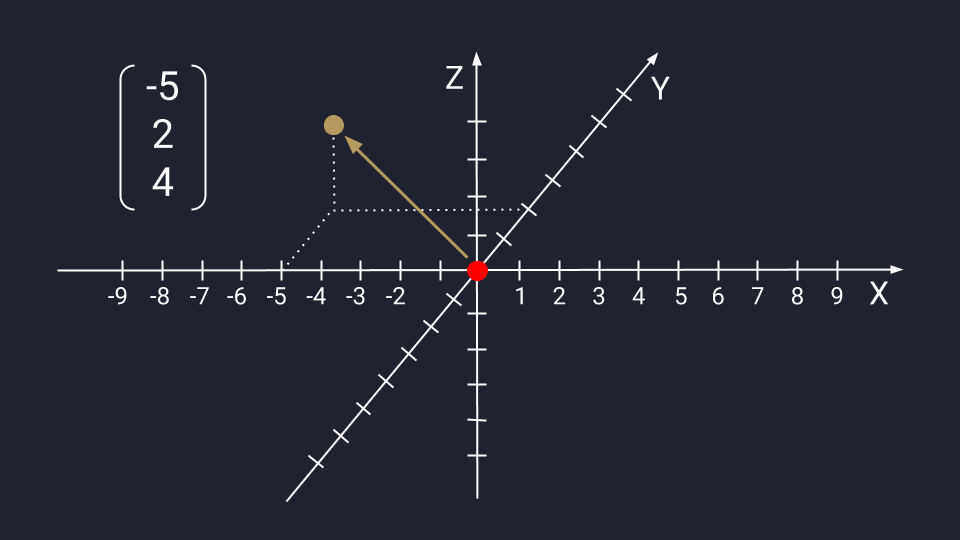Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке

Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Два вида физических величин: скалярные величины и векторные величины

«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.

Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:

• скалярная величина;
• векторная величина.

Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что

вектор — это направленный отрезок .

Стрелка — по-простому. У стрелки (вектора) есть длина (длина стрелки) и направление. Вектор — это нечто , что обладает длиной и направлением .

Примеры векторных величин: сила F ⃗ \vec F ⃗ , скорость V ⃗ \vec V ⃗ .

Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.

Может возникнуть вопрос: а как отличить векторную величину от скалярной ? Или так: как я узнаю, что передо мной вектор, а не скаляр?

Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.

А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.

Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.

Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.

Какие из представленных на рисунках величин являются скалярными, а какие — векторными?

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

• Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
• Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
• Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

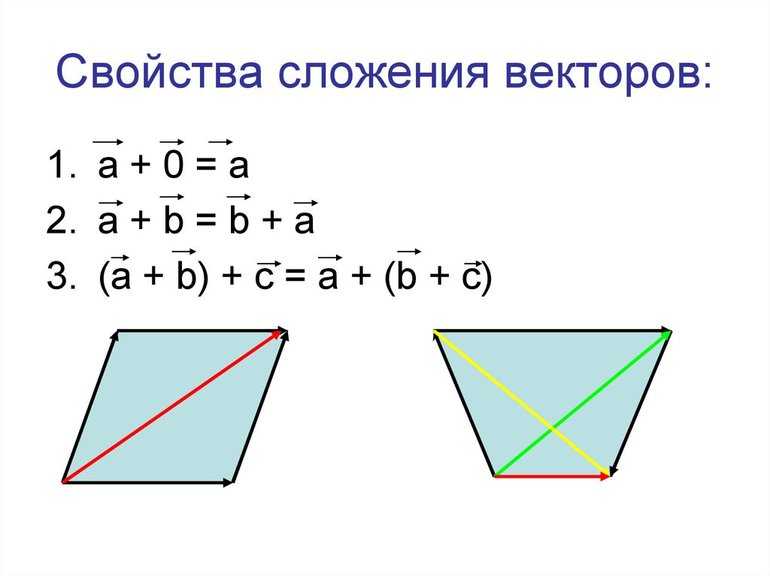
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.

И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Определение положительного скаляра и его измерения

Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.

Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).

Какая разница между вектором и скаляром?

Часто многим ученикам или даже студентам сложно понять отличия векторной и скалярной величины. Поэтому я хотел бы объяснить максимально понятным языком суть каждого из этих понятий и на примерах показать главные их отличия. Так как они оба часто используются в математических задачах, для правильного и быстрого решения которых нужно знать это.

Начнём с определений:

То есть у вас уже должна появиться основная картина, если есть направление у величины, то это вектор, а если нет, то это скаляр. Далее рассмотрим всё на конкретных примерах.

Пример 1. Когда какая-то сила действует на материальную точку, то она будет вектором, так как она обладает направлением. Так же и скорость материальной точки — тоже вектор.

Пример 2. А от уже температура тела будет скаляром, так как с ней не связано никакое направление. Поэтому масса тела и его плотность — тоже будут скалярами.

Если не учитывать направление векторной величины, то ее, как и скалярную, можно измерить, выбрав соответствующую единицу измерения. Но в этом случае полученное число, характеризует скалярную величину полностью, а векторную только частично. Её можно полностью охарактеризовать направленным отрезком, предварительно задав линейный масштаб. И это хорошо показано в следующем примере. Пример 3. Направленный отрезок АВ при введенном масштабе MN, изображающем единицу силы (1 Н) (более подробно смотрите на рисунке), характеризует силу в 3,5 Н, направление которой совпадает с направлением отрезка АВ (указанным стрелкой).

Думаю, после таких явных данных у вас уже не должно появиться проблем, при различии этих понятий.

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

• На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
• Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Что такое вектор

Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

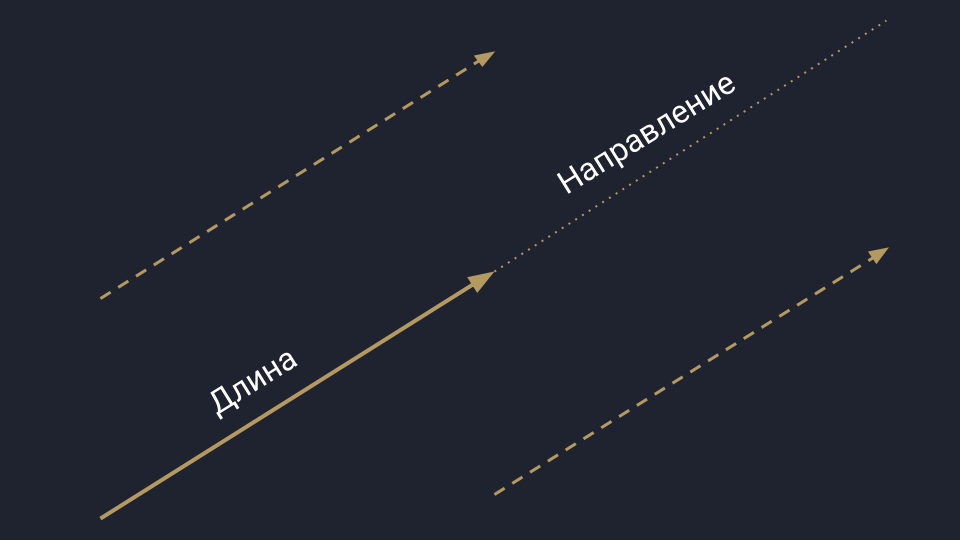Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

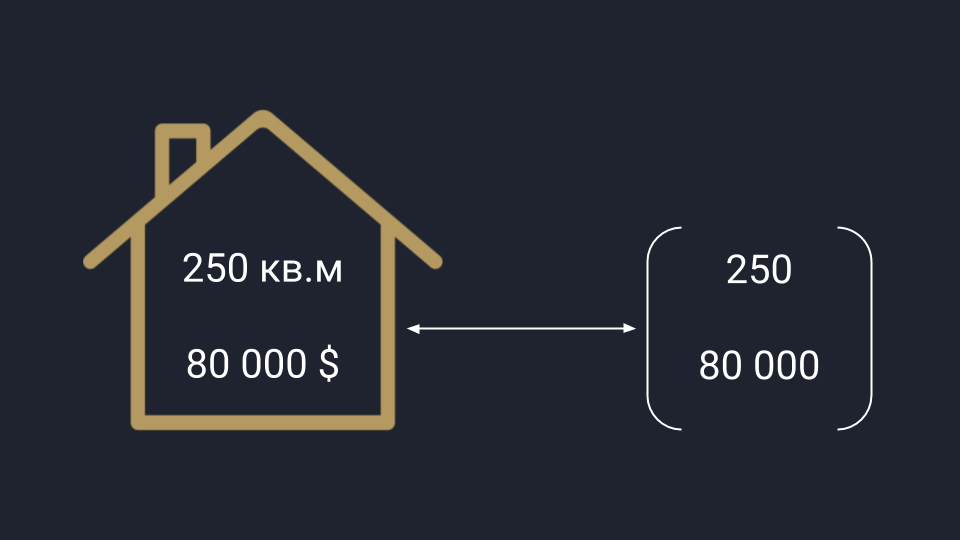Аналитическое представление вектора: данные можно перевести в числа

Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

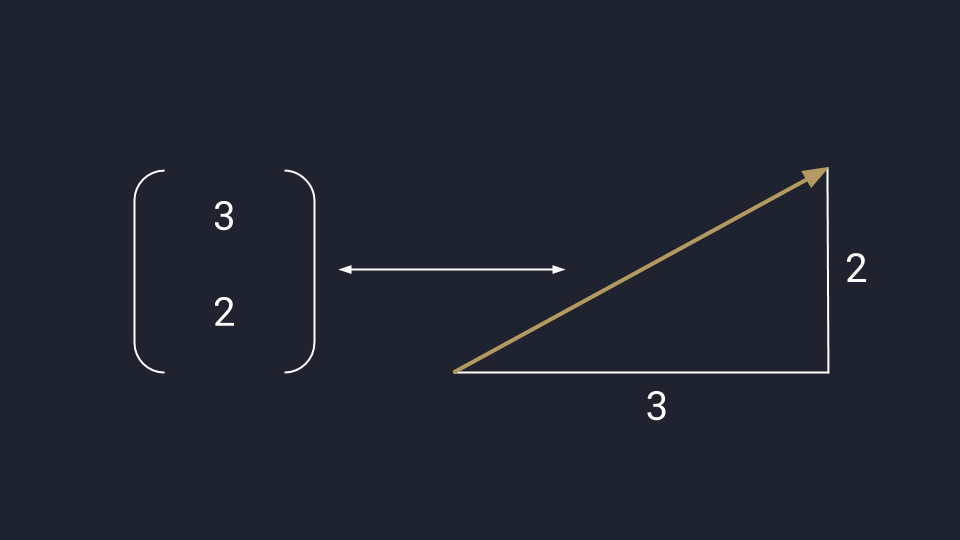Математическое представление вектора: данные можно перевести в числа или график

В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

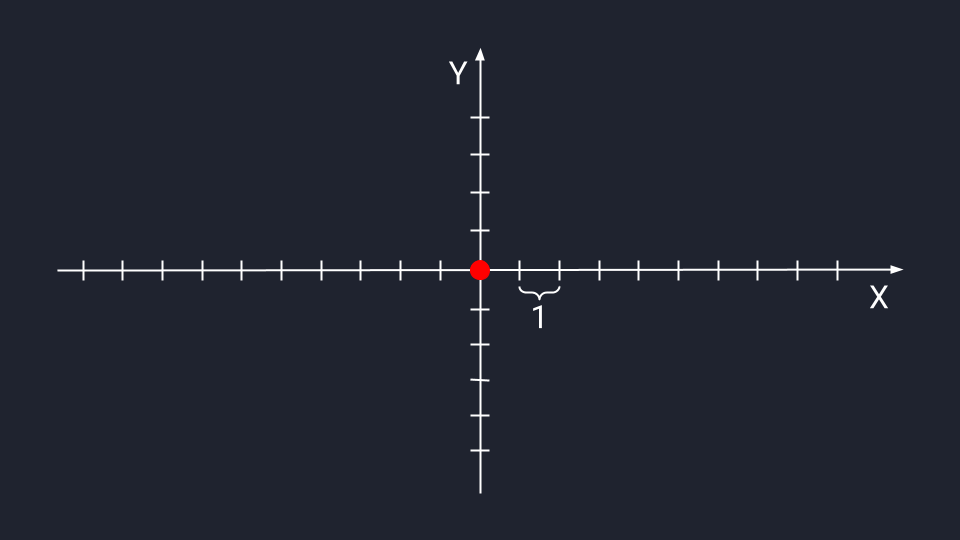Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

• Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
• Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
• Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

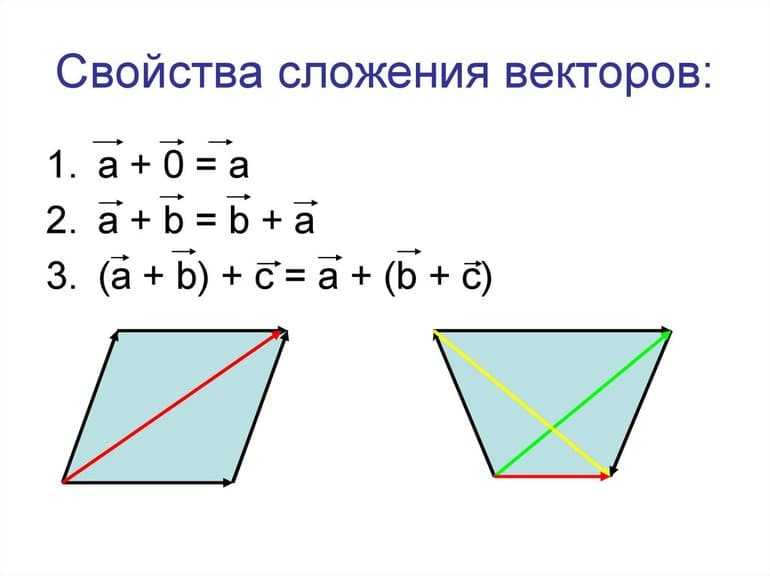
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Предыдущая запись Пружинный маятник — формулы и уравнения нахождения величин
Следующая запись Математический маятник — определение, формулы и принцип действия

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах .
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка .

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Перемещение — вектор, проведенный из начальной точки пути в конечную .

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

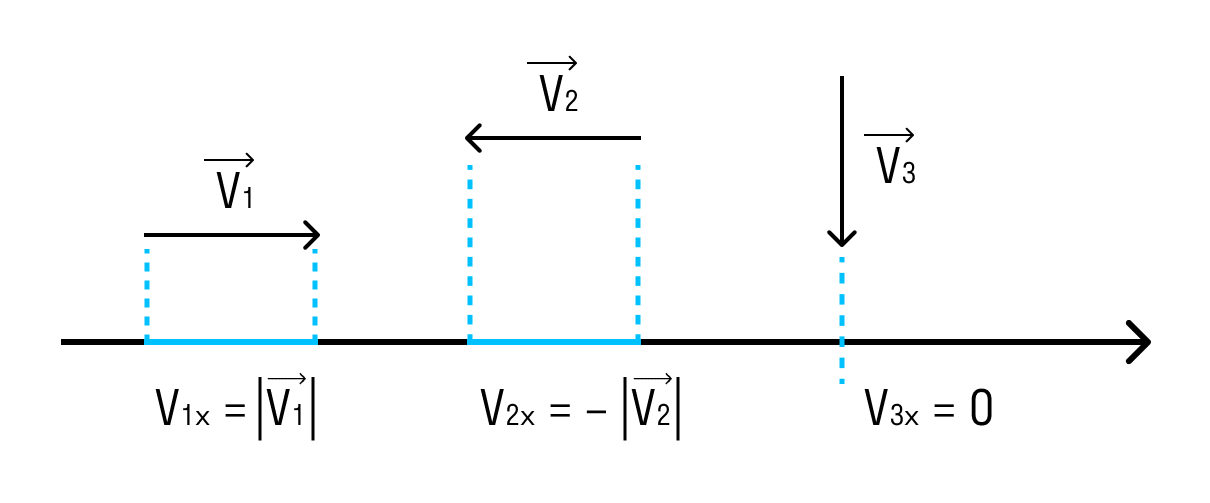
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость — скорость [м/с] — перемещение — время

Средняя путевая скорость V ср.путевая = S/t V ср.путевая — средняя путевая скорость [м/с] S — путь t — время

В чем разница между перемещением и путем? Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости

V ср.путевая = S/t

Подставим значения:

V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения x(t) = x + vxt x(t) — искомая координата в момент времени t x — начальная координата vx — скорость тела в данный момент времени [м/с] t — момент времени

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

Уравнение движения при движении против оси x(t) = x − vxt x(t) — искомая координата в момент времени t x — начальная координата vx — скорость тела в данный момент времени [м/с] t — момент времени

Что нужно знать о векторных величинах (векторах)

Векторы характеризуются модулем и направлением в пространстве

Модулем вектора называется его числовое значение.

Вектор изображают в виде направленного отрезка (стрелки). Стрелка указывает, куда направлен вектор (рис. 14, 15). Длина стрелки характеризует модуль вектора (рис. 16). Над буквенным обозначением вектора ставят стрелку, например:  

Модуль вектора обозначают той же буквой, но без стрелки над ней или символом  Например, модуль вектора на рисунке 16 равен

Модуль любого (не равного нулю) вектора — число положительное.

Векторы равны между собой, если равны их модули и одинаковы направления

Равные векторы лежат на одной и той же прямой или на параллельных прямых и направлены в одну и ту же сторону. На рисунке 17   Однако, несмотря на равенство модулей, так как у векторов различные направления.  

Угол между векторами

Чтобы найти угол между векторами (рис. 18, а), нужно совместить их начала (рис. 18, б). Если направления векторов одинаковы, то (рис. 18, в), если противоположны, то (рис. 18, г).

Умножение вектора на число

Произведение вектора на число есть вектор Чему в равен его модуль? Куда направлен вектор

Модуль вектора равен

Если то вектор направлен так же, как вектор а если то противоположно ему.

На рисунке 19 показаны результаты умножения вектора на 2, на 0,5, на (-3) и на (-1) соответственно. 

Противоположные векторы

Вектор называется противоположным вектору если У векторов одинаковые модули, но противоположные направления (рис. 19, а, г).

Сложение векторов

В 7-м классе вы складывали силы, направленные или одинаково, или в противоположные стороны. Результатом сложения в первом случае была сила, модуль которой равен а во втором

То же самое получается и при сложении векторов  (рис. 20). Если они направлены одинаково (рис. 20, а), то их сумма имеет модуль Если же направления векторов противоположны (рис

20, б), то модуль их суммы Обратите внимание: в последнем случае вектор направлен так, как вектор с большим модулем (т. е

как вектор ).  

А как сложить векторы, направленные под любым углом друг к другу? Для этого можно использовать любое из двух следующих далее правил. 

Правило параллелограмма

Совместим начала векторов (рис. 21, а), сохраняя их направления (рис. 21, б). Построим параллелограмм ABCD, принимая векторы за его стороны. Сумма векторов есть вектор совпадающий с диагональю АС параллелограмма: (см. рис. 21, б).

Правило треугольника

Совместим конец вектора с началом вектора сохраняя их направления (рис. 21, в). Вектор проведенный из начала вектора в конец вектора  равен сумме (см. рис. 21, в).

Из рисунков 21, б и 21, в ясно, что правило треугольника и правило параллелограмма дают одинаковые результаты. А как найти разность векторов?

Вычитание векторов

Пусть начала векторов совмещены (рис. 22). Проведем вектор из конца вычитаемого вектора в конец уменьшаемого вектора Вектор есть искомая разность:  Докажите с помощью построения, что Такой способ вычитания векторов очень удобен.

Правило многоугольника

Чтобы найти сумму нескольких векторов (например, ), каждый следующий вектор нужно проводить из конца предыдущего (рис. 23). Замыкающий вектор проведенный из начала первого вектора в конец последнего есть сумма данных векторов: 

Правило многоугольника следует из правила треугольника.

Модуль суммы векторов

Не путайте модуль суммы векторов, т. е. и сумму их модулей  Равенство  выполняется только для одинаково направленных векторов (см. рис. 20, а на с. 13). Во всех остальных случаях т. е. модуль суммы векторов меньше суммы их модулей. Так получается потому, что в любом треугольнике (см. рис. 21, в) длина одной стороны меньше суммы длин двух других сторон. Проверьте это на примерах.

Нуль-вектор

Пусть вектор равен вектору Тогда их разность т. е. нуль-вектору.

Главные выводы:

1. Векторные величины характеризуются модулем и направлением, скалярные — только числовым значением.
2. Сумму двух векторов находят по правилу параллелограмма или треугольника.
3. Разность двух векторов находят, проводя вектор из конца вычитаемого вектора в конец уменьшаемого (при совмещенных началах векторов).
4. Разность векторов можно найти как сумму
5. Произведение вектора на число есть вектор При направления векторов совпадают, а при — противоположны. Модуль вектора равен

§ 1. Векторы и скаляры

Cкаляр – это величина, которая характеризуется только числовым значением, а вектор – это величина, у которой, помимо числового значения, есть еще и направление

И векторные, и скалярные величины используются при описании того или иного движения, поэтому с самого начала важно научиться их различать

Представьте футбольный мяч, лежащий на траве. Кто-то слегка бьет по нему, в результате чего он перемещается вправо на некоторое расстояние, которое затем измеряется при помощи рулетки. Допустим, что мяч переместился на четыре метра. Это пройденное им в итоге расстояние называется путем.

Путь – это скалярная величина, ведь он характеризуется только числовым значением и ничего не говорит о направлении движения. Если бы нам сказали, что мяч переместился на четыре метра, оставалось бы только гадать, куда именно он переместился: вправо? влево? вверх? В рамках нашего обсуждения мы будем обозначать путь буквой d (от английского слова «distance», расстояние).

Если бы мы знали направление движения, если бы мы знали, что мяч переместился на четыре метра вправо, мы бы знали, какое перемещение совершило тело. Перемещение \vec{s} (от итальянского слова «spostamento», смещение) – это физическая величина, показывающая изменение положения объекта.

Перемещение – это вектор: у него есть и направление, и числовое значение. На письме это подчеркивается при помощи стрелочки: \vec{s}. Если же отбросить направление, мы получим модуль перемещения: \lvert\vec{s}\rvert или просто s.

В нашем случае модуль перемещения равен пройденному пути:

\lvert\vec{s}\rvert=d=4\thickspaceметра

Но так происходит далеко не всегда. Мы поговорим с вами об этом подробнее, когда придет время.

А теперь представим, что у наблюдателя, помимо рулетки, был еще и секундомер, с помощью которого он измерил время движения мяча. Допустим, это время равно двум секундам. С какой тогда скоростью двигался мяч? Ответить несложно: надо взять пройденное расстояние и разделить на время, в течение которого тело двигалось. В нашем случае скорость равна:

\dfrac{4\thickspaceм}{2\thickspaceс}=2\thickspaceм/с

При этом скорость бывает разной. Например, та скорость, которую мы только что получили, ничего не говорит нам о направлении движения. Ее мы можем назвать путевой скоростью. Эта скорость зависит от пройденного пути и является скалярной величиной. Мы будем обозначать эту скорость при помощи буквы v (от английского слова «velocity», скорость) и индекса «пут». В общем, v_{пут}.

Если бы мы разделили перемещение (четыре метра вправо) на время движения (две секунды), мы бы получили скорость перемещения – два метра в секунду вправо. Эта скорость является векторной величиной, и ее мы будем обозначать следующим образом: \vec{v}. В таком случае модуль скорости перемещения можно записать так: \lvert\vec{v}\rvert. Модуль скорости перемещения и путевая скорость – это не одно и то же. Впрочем, мы подробно рассмотрим этот вопрос чуть позже.

Подведем итоги. И у векторной, и у скалярной величины есть числовое значение, но у вектора также имеется какое-то направление. И это, по сути, все, что вам нужно запомнить. В будущем, используя эту простую идею, мы с вами получше разберемся в различиях между путем и перемещением, а также в различиях между путевой скоростью и скоростью перемещения.