Дифракция света. принцип гюйгенса-френеля. зоны френеля

Открытие интерференции. Опыт Юнга

Ученые конца XVII в. Роберт Бойль и Роберт Гук открыли интерференцию независимо друг от друга при наблюдениях за разноцветными тонкими масляными плёнками на воде. Томас Юнг в начале 1800-х гг. теоретически обобщил эти наблюдения и ввел в научный оборот само понятие интерференции света. Он также впервые продемонстрировал это явление в ходе опыта с использованием щелевых источников.

Для наблюдения интерференции нужны световые волны, колеблющиеся с одинаковой частотой, но не в одинаковой фазе. Из источников света только лазеры обладают свойством когерентности, однако получить ее можно разбив единый световой пучок на два или более, что и проделал Юнг во время своего знаменитого опыта.

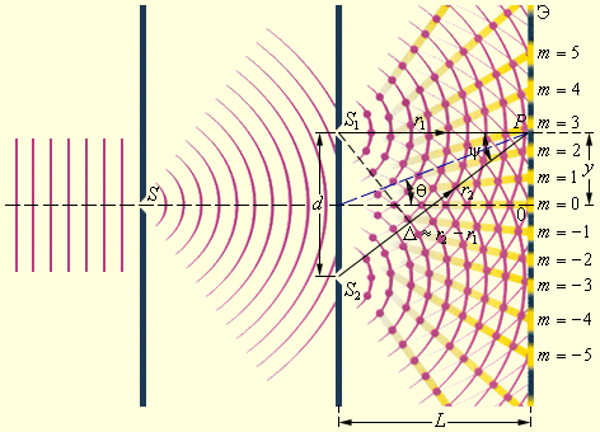Рисунок 1. Опыт Юнга. Автор24 — интернет-биржа студенческих работ

Щели $S_1$ и $S_2$ в опыте Юнга являются источниками вторичных волн, происходящих от источника $S$. Если щели расположены симметрично, то световые пучки от $S_1$ и $S_2$ порождают волны, колеблющиеся синфазно, но для наблюдателя, рассматривающего, например, точку $P$ под углом, они не будут выглядеть таковыми, поскольку свет от каждой из щелей проходит до этой точки разные расстояния $r_1$ и $r_2$, т.е. волны колеблются со сдвигом по фазе.

Замечание 1

Опыт Юнга экспериментальным путем доказывает, что волны от щелевых источников распространяются независимо друг от друга и складываются в точке наблюдения. Это явление известно как принцип суперпозиции.

Выразим разность между расстояниями, которое проходит свет как

$\Delta = r_2 — r_1$

Это расстояние называется разностью хода.

Для определения интенсивности свечения интерференционных полос на экране выразим каждую из световых волн как

$E = a \cdot \cos{(ω \cdot t – k \cdot r)}$, где:

• $a$ — амплитуда,
• $k$ — волновое число,
• $ω$ — круговая частота,
• $E$ — модуль вектора напряженности электромагнитного поля световой волны.

При сложении волн результирующее колебание можно выразить как

$E = a_1 \cdot \cos{(ωt – kr_1)} + a_2 \cdot \cos{(ωt – kr_2)} = A \cdot \cos{(ωt – φ)}$ ,

где $A$ — амплитуда результирующего колебания, а $φ$ — его фаза.

Интенсивность света, от которой зависит темная или светлая «окраска» интерференционных полос, принято выражать как квадрат амплитуды электрического поля волны:

$I = A^2$

Выразив амплитуду из предыдущих формул и подставив в уравнение интенсивности, получим, после тригонометрических преобразований:

$I = A^2 = a_1^2 + a_2^2 + 2 \cdot a_1 \cdot a_2 \cdot \cos{k \cdot \Delta} = I_1 \cdot I_2 + 2 \cdot \sqrt{I_1 \cdot I_2} \cdot \cos{k \cdot \Delta}$ ,

где $\Delta$ — разность хода.

По этой формуле можно вычислить интенсивность освещенности любой точки экрана, на который падает свет от взаимодействующих в процессе интерференции волн.

Применение интерференции в технике

Благодаря тому, что интерференционные изображения чувствительны к малейшим изменениям геометрии и оптической плотности прозрачных тел, интерференцию используют в технике для точных измерений. Особенно широко она примеряется в оптике.

Например, при шлифовке вогнутых зеркал для телескопов отклонения их поверхностей от геометрически правильной формы проверяют особым образом освещая и рассматривая отражение светового пучка на специальном экране. Характер расположения светлых и темных полос выявляет характер дефектов.

Просветление линз — еще одно применение интерференции в оптике. Объективы оптических устройств (фотоаппаратов, проекторов, перископов) представляют собой системы, состоящие из большого числа оптических компонентов (линз, призм, зеркал). Их стеклянные поверхности отражают около 5% попадающего на них света. Интерференция используется для снижения этих потерь. Для этого на поверхности оптических компонентов наносят тонкие пленки. Их толщину подбирают так, чтобы происходило гашение отражающегося света для длин волн зеленой (средней) части. Красные и фиолетовые лучи при прохождении через объективы ослабляются в меньшей степени, что, кстати, обуславливает сиреневые блики, испускаемые объективами в отраженном свете.

Интерферометры применяются также для анализа химического состава и физических характеристик (температуры, плотности) газов и других пропускающих свет веществ.

Принцип Гюйгенса-Френеля. Дифракція світла

Дифракцією називається сукупність явищ, що спостерігаються при поширенні світла в середовищі з різними неоднорідностями (поблизу границь непрозорих або прозорих тіл, через малі отвори) і які пов’язані із зміною напрямку поширення світлових хвиль (порівняно з напрямком, передбаченим геометричною оптикою).

Дифракція, зокрема, приводить до огинання світловими хвилями перешкод і проникнення світла в область геометричної тіні.

Між інтерференцією і дифракцією немає суттєвої фізичної відмінності.

 Інтерференція хвиль – це перерозподіл інтенсивності, який виникає в результаті суперпозиції хвиль, що збуджуються скінченним джерелом когерентних джерел.

Перерозподіл інтенсивності, який виникає внаслідок суперпозиції хвиль, що збуджуються когерентними джерелами, які розміщені неперервно, називається дифракцією хвиль.

Явище дифракції пояснюється за допомогою принципу Гюйгенса

кожна точка, до якої доходить хвиля, служить центром вторинних хвиль, а обвідна цих хвиль дає положення хвильового фронту в наступний момент часу.

Як приклад застосування принципу Гюйгенса розглянемо падіння плоскої хвилі на перешкоду з отвором (рис.220).

Коли хвильовий фронт доходить до перешкоди, то кожна точка отвору стає джерелом вторинних хвиль, а обвідна цих хвиль задає фронт хвилі, що пройшла через отвір. Цей фронт плоский лише в се­редній частині, а біля границі отвору відбувається загинання хвильового фронту, тобто хвиля проникає в область геометрич­ної тіні, огинаючи краї перешкоди.

Принцип Гюйгенса – суто геометричний спосіб побудови хвильових поверхонь –  розв’язує лише задачу про напрямок поширення хвильового фронту, але не зачіпає, по суті, питання про амплітуду, а отже, і про інтенсивність хвиль, що поширюються в різних напрямках. Френель вклав у принцип Гюйгенса фізичний зміст, доповнивши його ідеєю інтерференції вторинних хвиль.

•  Принцип Гюйгенса-Френе­ля можна виразити такими положеннями:
• 1).    під час розрахунку амплітуди світло­вих коливань, що збуджуються джерелом   в довільній точці М, джерело   можна замінити еквівалентною йому системою вторинних джерел – малих ділянок dS будь-якої замкненої допоміжної поверхні S, проведеної так, щоб вона охоплювала джерело   і не охоплювала розглядувану точку М;
• 2).    вторинні джерела, які еквівалентні джерелу  , когерентні між собою, тому вторинні хвилі, збуджені ними, інтерферують, і розрахунок інтерференції найбільш простий, якщо S – хвильова поверхня для світла джерела  , оскільки при цьому фази коливань всіх вторинних джерел однакові;

3).    амплітуда   коливань, що збуджуються в точці М вторинним джерелом, пропорційна до площі dSвідповідної ділянки хвильової поверхні обернено пропорційна до від­стані r від неї до точки М і залежить від кута   між зов­нішньою нормаллю до хвильової поверхні і напрямком від елемента dS до точки М (рис. 221):

,

де   – фаза коливань в місці розміщення хвильової поверхні, a – величина, яка пропорційна до амплітуди первинних хвиль в точках елемента dS;   монотонно спадає від 1 при   до при   (вторинні джерела не випромінюють назад); кут   називається кутом дифракції.

4).    якщо частина поверхні S закрита не­прозорими екранами, то вона не випро­мінює енергію, а інші випромінюють так само, як і за відсутності екранів.

Врахування амплітуд і фаз вторинних хвиль дозволяє в кожному конкретному випадку знайти амплітуду результуючої хвилі в довільній точці простору, тобто визначити закономірності поширення світла.

В загальному випадку розрахунок інтерференцій вторинних хвиль досить складний і громіздкий, однак для ряду випадків знаходження амплітуди результуючого коливання здійснюється алгебраїчним або геометричним додаванням.

1. Результуюче коливання в точці М є суперпозицією коливань , взятих для всієї хвильової поверхні S:
2. .
3. Ця формула є аналітичним виразом принципу Гюйгенса-Френеля.

Интерференция двух монохроматических волн

Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Рассмотрим идеализированный случай сложения двух монохроматических волн одинаковой частоты. Уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси X, имеет вид:

Если амплитуда и начальная фаза одинаковы во все моменты времени во всем пространстве, то волна называется однородной. Строго монохроматические волны никогда не могут быть точно реализованы в действительности и представляют идеализацию реальных волновых процессов. Условия применимости этой идеализации в каждой конкретной задаче требуют специального рассмотрения.

Пусть две плоские монохроматические волны одной частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления: и , где , .

Так как угол , то амплитуда результирующего колебания в данной точке определится выражением: , а интенсивность:

,

(2.4)

Если , , то интенсивность максимальна: , если , то интенсивность минимальна: .

Таким образом, при наложении двух монохроматических волн происходит устойчивое во времени перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. В тех точках пространства, для которых , результирующая интенсивность ; в точках, где , результирующая интенсивность .

Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: . Тогда в максимумах , в минимумах же . Для некогерентных волн при том же условии получается всюду одинаковая интенсивность .

Не нашли то, что искали? Воспользуйтесь поиском:

Интерференция света в тонких пленках

Картину интерференции часто можно наблюдать в тонких пленках, например, таких, какие образуются на поверхности воды при попадании на нее маслянистых прозрачных жидкостей. Такие вещества, будучи легче воды, растекаются по ее поверхности до тех пор, пока их толщина не будет представлять собой всего несколько слоев молекул. Это расстояние сопоставимо с длиной световой волны. К тому же наружная и внутренняя поверхности таких пленок параллельны с высокой точностью.

Интерференционная картина при попадании света на такую пленку получается потому, что часть пучка отражается от внешней ее стороны, а часть, пройдя сквозь пленку, отражается от внутренней.

Поскольку оптическая плотность пленки отличается от оптической плотности среды, из которой пришел световой пучок, световой луч преломляется при вхождении в пленку и выходе из нее. От точки, где такой луч выходит из пленки, может отразиться еше один луч, пришедший из того же источника. Таким образом, для наблюдателя эта точка будет выглядеть как источник двух независимых лучей, светящих с одной частотой, но с разностью по фазе, возникающей в результате задержки при прохождении первого луча сквозь пленку. Эта разность зависит от угла, под которым наблюдатель смотрит на точку, а математические закономерности, описывающие характеристики результирующей волны, будут такими же, как в опыте Юнга.

Особенностью интерференционной картины, порождаемой тонкими пленками, является то, что на них меняется не интенсивность освещения, а цвета, которые при изменении угла зрения «переливаются», создают радужные картины. Это связано с тем, что длина волны результирующего пучка настолько мала, что сопоставима с длинами волн различных цветов. Если пленка немного утончается (например, вследствие ветра, колышущего поверхность воды), цвет интерференционной картины смещается к синей стороне спектра, если утолщается — к красной.

Зависимость длины результирующей волны от толщины пленки можно описать формулой

$2dn = m \cdot \lambda$ ,

где $d$ — толщина пленки, $n$ — коэффициент, отражающий оптическую плотность вещества пленки и, следовательно, обуславливающий коэффициент преломления.

Кольца Ньютона

Еще одно проявление интерференции можно наблюдать в так называемых кольцах Ньютона. Увидеть их можно в ходе следующего опыта. Нужно положить выпуклую линзу на прозрачную пластину выпуклостью вниз. Верхняя поверхность линзы должна быть плоской. Если осветить такую систему монохроматическим (с постоянной длиной волны) светом сверху, то вокруг места соприкосновения линзы и пластинки образуется система из темных и светлых концентрических колец. Замерив диаметр одного из таких колец и определив его порядковый номер, можно узнать длину волны освещающего пучка. Чем больше выпуклость линзы, тем ближе друг к другу располагаются светлые и тёмные кольца.

Рисунок 2. Кольца Ньютона. Автор24 — интернет-биржа студенческих работ

Здесь, как и в случаях с опытом Юнга и тонкими пленками, мы имеем дело с распадением исходного светового пучка на два производных с той же длиной волны (частотой), но сдвинутых по фазе за счет преломления в линзе и ее геометрии.

Зависимость между радиусом кольца $r$, кривизной линзы $R$ и длиной волны $\lambda$ описывается формулой

$r = \sqrt{R \cdot k \cdot \lambda}$ .

Построение изображений в линзах

Для построения изображения в линзах следует помнить:

1. луч, идущий вдоль главной оптической оси линзы, не преломляется;
2. луч, проходящий через оптический центр линзы, не преломляется;
3. луч, падающий на собирающую линзу параллельно главной оптической оси, после преломления пройдет через фокус линзы;
4. луч, падающий на рассеивающую линзу параллельно главной оптической оси, преломится так, что его мнимое продолжение пройдет через фокус линзы, а сам луч – противоположно мнимому продолжению;
5. луч, падающий на собирающую линзу через фокус, после преломления пройдет параллельно главной оптической оси линзы;
6. произвольный луч после преломления в собирающей линзе пойдет через побочный фокус (точку фокальной плоскости, в которой ее пересечет параллельная произвольному лучу побочная оптическая ось);
7. произвольный луч, падающий на рассеивающую линзу, преломится так, что его мнимое продолжение пройдет через точку, в которой пересечет фокальную плоскость линзы побочная оптическая ось, параллельная произвольному лучу.

Изображение, даваемое тонкой линзой, может быть действительным или мнимым.

Действительное изображение получается в результате пересечения преломленных в линзе лучей, исходящих из данной точки.

Мнимое изображение получается в результате пересечения продолжений преломленных в линзе лучей, исходящих из данной точки.

Построение изображений точки, даваемых собирающей линзой

Если точка находится за двойным фокусом линзы, то ее действительное изображение получается между фокусом и двойным фокусом по другую сторону от линзы.

Если точка находится в двойном фокусе линзы, то его действительное изображение получается в двойном фокусе по другую сторону от линзы.

Если точка находится между фокусом и двойным фокусом линзы, то его действительное изображение получается за двойным фокусом по другую сторону от линзы.

Если точка находится в фокусе линзы, то его изображение находится в бесконечности.

Если точка находится между линзой и фокусом, то его мнимое изображение получается по ту же сторону от линзы.

Построение изображений предмета, даваемых собирающей линзой

Если предмет находится за двойным фокусом линзы, то его изображение получается действительным, перевернутым, уменьшенным, по другую сторону от линзы.

Если предмет находится в двойном фокусе линзы, то его изображение получается действительным, перевернутым, равным по размерам предмету, в двойном фокусе по другую сторону от линзы.

Если предмет находится между фокусом и двойным фокусом линзы, то его изображение получается действительным, перевернутым, увеличенным, по другую сторону от линзы.

Если предмет находится в фокусе линзы, то его изображение находится в бесконечности.

Если предмет находится между линзой и фокусом, то его изображение получается мнимым, прямым, увеличенным, по ту же сторону от линзы.

Построение изображений точки, даваемых рассеивающей линзой

В рассеивающей линзе изображение точки всегда получается мнимым, по ту же сторону от линзы.

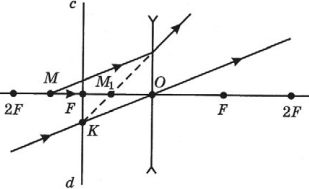
Построение изображений предмета, даваемых рассеивающей линзой

Изображение предмета в рассеивающей линзе всегда получается мнимым, прямым, уменьшенным, по ту же сторону от линзы.

Важно!
При решении задач на прохождение световых лучей сквозь линзы и получение изображений в них прежде всего выясните, о какой линзе идет речь: собирающей или рассеивающей. Обязательно сделайте чертеж, на котором соответствующими буквами укажите все основные расстояния: расстояние от предмета до линзы, расстояние от линзы до изображения, фокусное расстояние. Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы

Также обязательно укажите оптический центр линзы и оба фокуса по разные стороны от линзы.

При построении изображения следует заранее выучить, каким оно должно быть при соответствующем расположении предмета относительно линзы и где находиться (действительным или мнимым, увеличенным или уменьшенным, прямым или обратным). В противном случае при неверном построении, когда вы чуть-чуть искривите луч или он пойдет неточно через фокус или центр, изображение может оказаться не там, где надо, или вместо увеличенного уменьшенным, и тогда в решении появится ошибка.

Принцип Гюйгенса — Всё для чайников

Подробности Категория: Оптика

Законы отражения и преломления света можно вывести из одного общего принципа, описывающего поведение волн. Этот принцип впервые был выдвинут современником Ньютона Христианом Гюйгенсом.

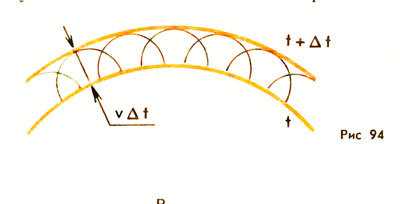
Принцип Гюйгенса. Согласно принципу Гюйгенса каждая точка среды, до которой дошло возмущение, сама становится источником вторичных волн.

Для того чтобы, зная положение волновой поверхности в момент времени t, найти ее положение в следующий момент времени t +Δt, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени (рис. 94).

Этот принцип в равной мере пригоден для описания распространения волн любой природы: механических, световых и т. д. Гюйгенс сформулировал его первоначально именно для световых волн.

Закон отражения. С помощью принципа Гюйгенса можно вывести закон, которому подчиняются волны при отражении от границы раздела сред.

Рассмотрим отражение плоской волны. Волна называется , плоской если поверхности равной фазы (волновые поверхности) представляют собой плоскости. На рисунке 95     MN — отражающая поверхность, прямые А1А и В1В— два луча падающей плоской волны (они параллельны друг другу). Плоскость АС—волновая поверхность этой волны.

Угол а между падающим лучом и перпендикуляром к отражающей поверхности в точке падения называют углом падения.Волновую поверхность отраженной волны можно получить, если провести огибающую вторичных волн, центры которых лежат на границе раздела сред. Различные участки волновой поверхности АС достигают отражающей границы неодновременно.

Возбуждение колебаний в точке А начнется раньше, чем в точке В, на время Δt=CB/v (v — скорость волны).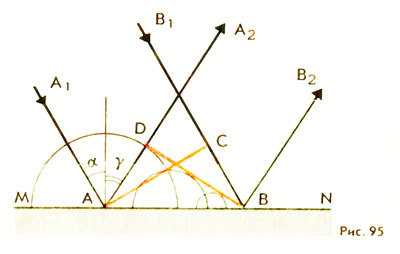

В момент, когда волна достигнет точки Вив этой точке начнется возбуждение колебаний, вторичная волна с центром в точке А уже будет представлять собой полусферу радиусом r = AD = vΔt = CB. Радиусы вторичных волн от источников, расположенных между точками А и В, меняются так, как показано на рисунке 95. Огибающей вторичных волн является плоскость , касательная к сферическим поверхностям. Она представляет собой волновую поверхность отраженной волны. Отраженные лучи АА2 и ВВ2 перпендикулярны волновой поверхности    DB. Уголϒ между перпендикуляром к отражающей поверхности и отраженным лучом называют углом отражения.

Так как AD=СВ и треугольники ADB и АСВ прямоугольные, то ∠ DBA = ∠CAB и ϒ=∠DBA как углы с перпендикулярными сторонами. Следовательно, угол отражения равен углу падения:

а=ϒ

Кроме того, как вытекает из построения Гюйгенса, падающий луч, луч отраженный и перпендикуляр, восставленный в точке падения, лежат в одной плоскости.

Эти два утверждения представляют собой закон отражения света.Если обратить направление распространения световых лучей, то отраженный луч станет падающим, а падающий — отраженным.

Обратимость хода световых лучей — их важное свойство. Сформулирован общий принцип распространения волн любой природы — принцип Гюйгенса. Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент

Из принципа Гюйгенса выведен закон отражения волн

Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент. Из принципа Гюйгенса выведен закон отражения волн

Сформулирован общий принцип распространения волн любой природы — принцип Гюйгенса. Этот принцип позволяет с помощью простых геометрических построений находить волновую поверхность в любой момент времени по известной волновой поверхности в предшествующий момент. Из принципа Гюйгенса выведен закон отражения волн.

Измерение скорости света               

Механические модели волн. 1.                

Механические модели волн. 2.                 

Диаграмма направленности диполя                  

Спектр модулированного колебания                  

Принцип суперпозиции. Модель на осциллографе                   

Частота сигнала и характерное время прибора                    

«Стоячая волна» на экране осциллографа                    

Проблема когерентности волн

Для возникновения интерференционных полос недостаточно двух источников света, излучающих с одинаковой частотой. В повседневной жизни можно видеть множество примеров, когда при наличии таких источников (например, светящихся одноцветных светодиодов в гирлянде) никаких светлых и темных полос не возникает.

В реальности световые волны, за исключением тех, что излучают некоторые лазеры, не совпадают по частоте с достаточной для появления интерференционной картины точностью. Источник света состоит из атомов, излучающих свет независимо друг от друга в хаотической последовательности и с интервалами порядка $\tau = 10^{–8}$ с.

Это можно объяснить следующим образом. Результирующие волны от очень большого числа источников существует в течение очень краткого периода времени, после чего в процесс вступает другая группа излучающих атомов. Суммарное излучение меняет амплитуду и фазу, т.е. интерференционная картина появляется на чрезвычайно малые моменты времени, неразличимые с помощью оптических приборов. Фрагменты испускаемого света продолжительностью $\tau$ называют цугами. Их длина в пространстве равна $c \cdot τ$, где $c$ – скорость света. Фазы разных цугов не совпадают, поэтому мы видим не интерференционную картину, а хаотический по фазе набор цугов, т.е. эти колебания некогерентны, а интерференционные полосы хаотически перемещаются и глаз или фотоприбор вместо них видит лишь точки с усредненной освещенностью.

Нестационарная интерференция света

К ней от­но­сят­ся све­то­вые бие­ния, на­блю­даю­щие­ся при на­ло­же­нии све­то­вых по­лей разл. час­тот. В этом слу­чае воз­ни­ка­ет бе­гу­щая в про­стран­ст­ве ин­тер­фе­рен­ци­он­ная кар­ти­на, так что в за­дан­ной точ­ке про­стран­ст­ва ин­тен­сив­ность све­та пе­рио­ди­че­ски ме­ня­ет­ся во вре­ме­ни с час­то­той, рав­ной раз­но­сти час­тот ин­тер­фе­ри­рую­щих волн. Бие­ния воз­ни­ка­ют в обыч­ных (не­ла­зер­ных) схе­мах И. с. при из­ме­не­нии во вре­ме­ни раз­но­сти хо­да ин­тер­фе­ри­рую­щих лу­чей. При­ме­ром мо­жет слу­жить ин­тер­фе­ро­метр Май­кель­со­на с пе­ре­мен­ной дли­ной од­но­го из плеч. При пе­ре­ме­ще­нии вдоль лу­ча све­та од­но­го из зер­кал ин­тен­сив­ность све­та на вы­хо­де ин­тер­фе­ро­мет­ра пе­рио­ди­че­ски ме­ня­ет­ся, что мо­жет слу­жить сред­ст­вом из­ме­ре­ния ско­ро­сти очень мед­лен­ных пе­ре­ме­ще­ний. Напр., при дви­же­нии зер­ка­ла со ско­ро­стью 10–6 м/с ин­тен­сив­ность све­та ме­ня­ет­ся с час­то­той ок. 4 Гц.

Бие­ния мо­гут на­блю­дать­ся и в из­лу­че­нии не­за­ви­си­мых ис­точ­ни­ков све­та. Для это­го их яр­ко­сти и спек­траль­ные плот­но­сти из­лу­че­ния долж­ны быть очень ве­ли­ки. Обе эти ха­рак­те­ри­сти­ки вы­ра­жа­ют­ся че­рез па­ра­метр вы­ро­ж­де­ния фо­то­нов $ρ$, рав­ный чис­лу фо­то­нов в объ­ё­ме ко­ге­рент­но­сти. При фо­то­элек­трич. ре­ги­ст­ра­ции бие­ний па­ра­метр $ρ$ в про­из­ве­де­нии с кван­то­вым вы­хо­дом при­ём­ни­ка оп­ре­де­ля­ет ве­ли­чи­ну сиг­на­ла бие­ний по от­но­ше­нию к фо­ну фо­тон­но­го шу­ма. Из­лу­че­ние ла­зе­ров силь­но вы­ро­ж­де­но $(ρ≫1)$, вслед­ст­вие че­го бие­ния в све­те двух ла­зе­ров и ме­ж­ду разл. ти­па­ми ко­ле­ба­ний од­но­го ла­зе­ра лег­ко на­блю­да­ют­ся. Эти бие­ния час­то иг­ра­ют вред­ную роль как ис­точ­ник мощ­но­го шу­ма ла­зе­ра.

Для те­п­ло­вых ис­точ­ни­ков обыч­но $ρ≪1$, по­это­му эф­фек­ты не­ста­цио­нар­ной И. с. в их из­лу­че­нии край­не ма­лы. Тем не ме­нее их уда­лось об­на­ру­жить в тон­ких экс­пе­ри­мен­тах по кор­ре­ля­ции ин­тен­сив­но­стей.

И. с. ис­поль­зу­ет­ся при спек­траль­ном ана­ли­зе све­та, для точ­но­го из­ме­ре­ния рас­стоя­ний, уг­лов, ско­ро­стей, в реф­рак­то­мет­рии. Боль­шое зна­че­ние ин­тер­фе­ро­мет­рия име­ет в оп­тич. про­из­вод­ст­ве как сред­ст­во кон­тро­ля ка­че­ст­ва по­верх­но­стей и лин­зо­вых сис­тем. Ин­тер­фе­рен­ци­он­ные яв­ле­ния ис­поль­зу­ют­ся для соз­дания све­то­фильт­ров, вы­со­ко­ка­че­ст­вен­ных зер­кал, про­свет­ляю­щих по­кры­тий для оп­тич. де­та­лей. И. с. со­став­ля­ет ос­но­ву оп­тич. го­ло­гра­фии.

Расчет интерференционной картины от двух источников.

Расчет интерференционной картины от
двух когерентных источников.

Рассмотрим две когерентные световые
волны, исходящие из источников
и(рис.1.11.).

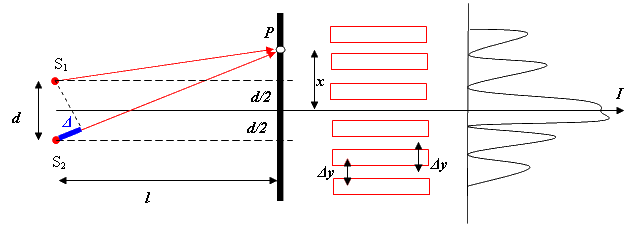
Экран для наблюдения интерференционной
картины (чередование светлых и темных
полос) поместим параллельно обеим щелям
на одинаковом расстоянии
.Обозначим
за x — расстояние от центра интерференционной
картины до исследуемой точки Р на
экране.

Расстояние между источниками
иобозначим
какd. Источникиирасположены
симметрично относительно центра
интерференционной картины. Из рисунка
видно, что

Следовательно

и оптическая разность хода равна

Разность хода
составляет
несколько длин волн и всегда значительно
меньшеи,
поэтому можем считать, чтои.
Тогда выражение для оптической разности
хода будет иметь следующий вид:

Так как расстояние от источников до
экрана во много раз превосходит
расстояние от центра интерференционной
картины до точки наблюдения
,
то можно допустить, чтот.
е.

Подставив значение
(1.95)
в условие (1.92) и выразив х, получим, что
максимумы интенсивности будут наблюдаться
при значениях

, (1.96)

где
—
длина волны в среде, аm— порядок
интерференции, ах max —
координаты максимумов интенсивности.

Подставив (1.95) в условие (1.93), получим
координаты минимумов интенсивности

, (1.97)

На экране будет видна интерференционная
картина, которая имеет вид чередующихся
светлых и темных полос. Цвет светлых
полос определяется светофильтром,
используемым в установке.

Расстояние между соседними минимумами
(или максимумами) называется шириной
интерференционной полосы. Из (1.96) и
(1.97) следует, что эти расстояния имеют
одинаковое значение. Чтобы рассчитать
ширину интерференционной полосы, нужно
из значения координаты одного максимума
вычесть координату соседнего максимума

Для этих целей можно использовать и
значения координат двух любых соседних
минимумов.