Дизъюнкция

Логические операции

Операции логического типа очень часто применяются при построении выражений, используемых в программировании. К ним относятся следующие:

1. Конъюнкция.
2. Дизъюнкция.
3. Инверсия.

Однако булева алгебра не ограничивается только ими, поскольку существуют и другие их производные. Для каждой из трех составляются определенные таблицы истинности, которые каждый раз необходимо строить для получения результата вычисления логических выражений. Специалисты рекомендуют отдельно на листе картона перечертить таблицы всех логических операций.

Функция конъюнкции

Конъюнкция — операция логического умножения, которая будет истинным при достоверности каждого выражения. Ее обозначение — символ конъюнктора «&». Записывается следующим образом: S&T, где S и T — логические тождества или конкретные значения. Операция имеет такие особенности: только при равенстве всех элементов 1 значение выражения является истинным, а в других случаях — ложью. Для проверки необходимо составить таблицу значений логического тождества:

S	T	S&T
F
1	F
1	F
1	1	T

Таблица 1. Значение функции в зависимости от логических переменных.

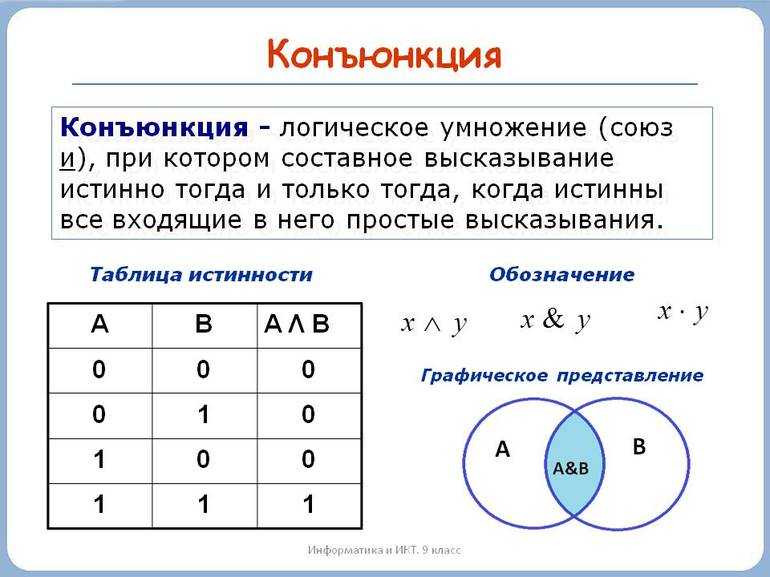
Из таблицы 1 видно, что выражение S&T принимает только TRUE при всех истинных значениях переменных. Если рассматривать алгебру, то можно провести аналогию между логическим и обыкновенным умножениями. Например, произведение двух чисел S*T, которые для удобства сравнения принимают значения 0 или 1.

Информация о дизъюнкции

В булевой алгебре операция логического сложения называется дизъюнкцией. Обозначается она символом, который называется дизъюнктором (V или I). Логическое тождество, содержащее два элемента, имеет такой вид: SVT. Операция имеет только ложное значение при равенстве S и T нулю. Для нее нужно также строить специальную таблицу:

S	T	Результат — S|T
1	1
1	1
1	1	1

Таблица 2. Истинность операции дизъюнкции SVT.

Операция аналогична сложению в алгебре, хотя имеются некоторые отличия. Чтобы убедиться в этом, требуется выполнить определенное действие — построить специальную таблицу результатов для алгебраического сложения нулей и единиц.

Если рассмотреть результаты в последнем случае, то можно сделать вывод о схожести сложения и дизъюнкции. Однако в последней строке алгебраической суммы есть некоторое несоответствие — 2. Это показывает, какое переполнение разряда происходит в булевой алгебре. В последней происходит переход с одного разряда в другой.

Булево отрицание

В алгебре логики применяется также операция отрицания, которую также называют инверсией. Суть ее заключается в том, что при истинном значении выражения под знаком инверсии получается ложный результат, а при ложном — истина. Обозначается она символом инверсии «¬», а записывается в таком виде ¬(S). Для демонстрации операции необходимо ознакомиться с таблицей:

Исходное выражение, S	Результат, ¬(S)
T
1	F

Таблица 3. Истинность ¬(S).

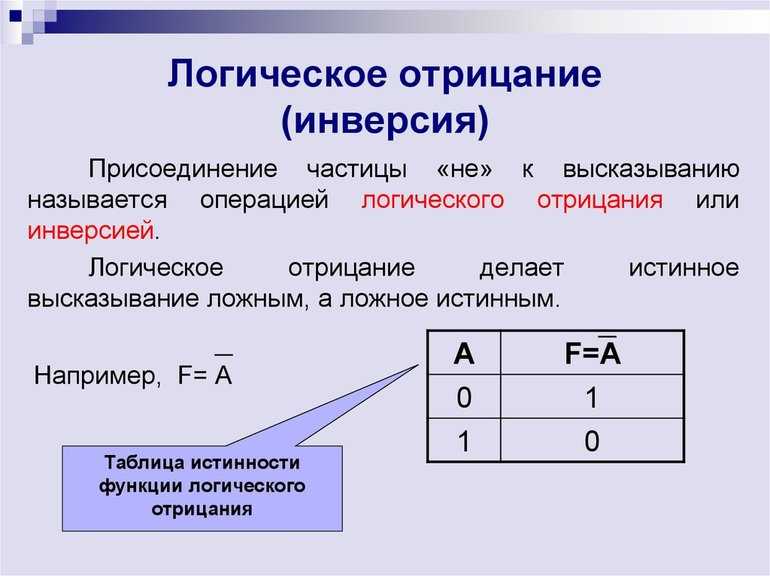
Следует отметить, что операция инверсии функции прибавляет к искомому выражению частицу «НЕ». Очень часто используется при построении логических условий. В алгоритмах и языках программирования отрицание записывается в виде комбинации следующих символов: «<!» (не меньше), «=!» (не равно) и «>!» (не больше).

Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t<0)&(t>0). При использовании логического отрицания условие выглядит короче: t=!0.

Приоритеты вычислений

При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:

1. Написать выражение: S&T|S|.
2. Определить последовательность вычислений: , S&T, |S и v.
3. Составить обобщенную таблицу.

Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:

1. ¬(0)=1.
2. ¬(1)=0.
3. ¬(¬(0))=0.
4. ¬(¬(1))=1.
5. ¬(S&T)=¬(S)&¬(T).
6. S&(S|T)=S|T.

Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.

Обозначения

Наиболее часто встречаются следующие обозначения для операции дизъюнкции:

\displaystyle{ a \lor b, \; a } || \displaystyle{ b, \; a } | \displaystyle{ b, \; a~\mbox{OR}\,\,b }\displaystyle{ , \; \max(a,b). }

При этом обозначение \displaystyle{ a \lor b }, рекомендованное международным стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике. Появилось оно не сразу: Джордж Буль, положивший начало систематическому применению символического метода к логике, не работал с дизъюнкцией (используя вместо неё строгую дизъюнкцию, которую обозначал знаком +), а Уильям Джевонс предложил для дизъюнкции знак . Эрнст Шрёдер и П. С. Порецкий вновь использовали знак +, но уже применительно к обычной дизъюнкции. Символ \displaystyle{ \lor } как обозначение дизъюнкции впервые встречается в статье «Математическая логика, основанная на теории типов»Бертрана Рассела (1908); он образован от лат. vel, что означает «или».

Обозначение для дизъюнкции было использовано и в раннем языке программирования Алгол 60. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для дизъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения и (с возможностью замены последнего на ключевое слово ); в языках Паскаль и Ада используется зарезервированное слово ; в языках C и C++ применяются обозначения для побитовой дизъюнкции и для логической дизъюнкции).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что \displaystyle{ 0 \lt 1 }), оказывается, что \displaystyle{ (a \lor b)\,=\,\max(a,b). } Таким образом, дизъюнкция оказывается частным случаем операции вычисления максимума; это открывает наиболее естественный способ определить операцию дизъюнкции в системах многозначной логики.

Чтобы лучше понять тему

В сети сделано и размещено немало калькуляторов, при помощи которых можно судить об истинности высказываний. Но хороший программист должен самостоятельно уметь производить соответствующие подсчеты. Операцией логического характера не является выражение, результатом которого не выступает:

• понимание смысла;
• изменение содержания или объема;
• образование новых понятий.

Логическое выражение в программировании обычно предусматривает работу с операторами:

• XOR;
• IF;
• IF…Else.

А для того, чтобы лучше понимать соответствующую тему, рекомендуется пройти онлайн курсы дистанционно. Они помогут быстрее вникнуть в особенности программирования, коддинга и выбранных языков. По выпуску ученику будет выдан сертификат, указывающий на наличие знаний в выбранном направлении. Так логическое выражение и упомянутые ранее операции не доставят никаких хлопот даже новичку-разработчику.

Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!

Также, возможно, вам будет интересен следующий курс:

Основные операции

Математика, информатика, программирование и другие науки немыслимы без анализа, а также построения теорий по заданным вопросам. Здесь без мышления логического характера не обойтись. Соответствующий момент активно применяется в приложениях — не только сложных, но и элементарных.

Чтобы понять, как работает логи ческая цепочка в калькуляторах истинности, стоит запомнить ключевые операции над логическими выражениями. Всего их несколько:

• конверсия;
• дизъюнкция;
• конъюнкция;
• строгая дизъюнкция;
• импликация;
• эквивалентность.

В программировании также стоит обратить внимание на запись исключающего или. Это – операция XOR

Информация в информатике

Понятие данного термина в информатике имеет целый ряд свойств. К таким свойствам относятся следующие:

• Достоверность,
• Релевантность,
• Полнота,
• Эргономичность,
• Актуальность,
• Защищённость,
• Доступность.

Информация является особым видом ресурсов, который обладает свойствами, характерными именно для него. К таким свойствам относятся следующие:

• Стираемость,
• Запоминаемость,
• Преобразуемость,
• Передаваемость,
• Воспроизводимость.

Рассмотрим каждое из данных свойств более подробно.

1. Запоминаемость является одним из самых главных свойств данных. Запоминаемую информацию принято называть макроскопической. При этом имеются в виду пространственные масштабы запоминающей ячейки, а также время запоминания. С макроскопическими данными люди имеют дело на реальной практике.
2. Передача происходит с помощью специальных каналов связи, в том числе и с помехами. Передаваемость хорошо исследована на основе теории Шеннона. В этом случае имеется в виду немного другой аспект, заключающийся в способности сведений к их копированию, таким образом, она может быть запоминающейся другой макроскопической системой, одновременно с этим оставаясь тождественной самой себе. Становится очевидным, что при копировании количество данных не будет возрастать.
3. Говоря о воспроизводимости сведений, необходимо отметить, что она тесно связывается с ее передаваемостью, но не относится к ее независимому базовому свойству. Если же под передаваемостью имеется в виду, что не стоит считать существенными пространственные отношения между отдельными частями системы, среди которых передаются данные, то воспроизводимость характеризуется неиссякаемостью и неистощаемостью сведений, то есть во время копирования сведений будет оставаться тождественной самой себе.
4. Преобразуемостью называется фундаментальное свойство данных. Она подразумевает то, что сведения могут сами поменять форму и способ своего существования. Копируемость при этом является разновидностью преобразования сведений, но ее количество при этом не меняется. Говоря об общем случае, стоит отметить, что количество данных в процессе преобразования будет меняться, но не будет возрастать.
5. Стираемость тоже относится к независимому свойству сведений. Стираемость связана с таким преобразованием данных, во время которого ее количество снижается или становится равным нулю.

Разделительное суждение или дизъюнкция (от лат. disjunction – разобщение)

Используется союз или (либо).

Поскольку союз или (либо) употребляется в естественном языке в двух значениях – соединительно-разъединительном и исключающе-разделительном, то следует различать и два типа дизъюнкции:

1. 1. слабую (нестрогую) и
   2. сильную (строгую).

Соединительно-разделительное суждение (слабая дизъюнкция) – это сложное суждение, в котором входящие в него простые суждения не исключают друг друга.

Например: «Ученик может допустить в диктанте орфографическую или пунктуационную ошибку».

В данном примере два простых суждения, соединенных между собой союзом или:

1. «Ученик может допустить в диктанте орфографическую ошибку»,
2. «Ученик может допустить в диктанте пунктуационную ошибку».

Поскольку ученик может допустить в диктанте либо только орфографическую, либо только пунктуационную ошибку, либо и ту, и другую – это суждение является слабой дизьюнкцией. Члены подобного суждения не исключают друг друга.

Слабая дизъюнкция обозначается знаком «v».

Схема суждения «а v в» читается «А или В».

Исключающе-разделительное суждение  (строгая дизъюнкция) – это сложное суждение, в котором входящие в него простые суждения исключают друг друга.

Например: «Человек либо жив, либо мертв».

В данном примере два простых суждения, соединенных между собой союзом либо:

1. «Человек жив»,
2. «Человек мертв».

Строгая дизъюнкция обозначается галочкой с точкой наверху. Суждение читается: «либо А, либо Б». Члены строгой дизъюнкции исключают друг друга, поэтому называются альтернативами.

Примеры

Следующие предложения являются высказываниями:

%%A_1%%: «Лондон — столица Австрии».
%%A_2%%: «Число 8 больше числа 3».
%%A_3%%: «Число 8 больше числа 13».
%%A_4%%: «Луна — спутник планеты Земля».

Причем высказывания %%A_1, A_3%% — ложные, а %%A_2, A_4%% — истинные.

Следующие предложения не являются высказываниями:

%%B_1%%: «Какой сегодня день недели?».
%%B_2%%: «%%2 + 3%%».
%%B_3%%: «Число %%x%% больше 3».

Мы не можем сказать о любом из высказываний %%B_1, B_2, B_3%% истинно оно или ложно. Например, в предложении %%B_3%% буква %%x%% — переменная. Если поставить какое либо значение вместо нее, например 8, то получим истинное высказывание.

Примечания

1. Гутников В. С. . Интегральная электроника в измерительных приборах. — Л.: Энергия, 1974. — 144 с. — С. 14—16.
2. , с. 534.
3. Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 320, 349, 352, 368.
4. . // Website Jeff Miller Web Pages. Дата обращения: 5 февраля 2016.
5. , с. 149—150.
6. , с. 30.
7. Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
8. Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
9. Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
10. Эллис М., Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
11. Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
12. Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.

Связь с естественным языком

В естественном языке операция «сложение по модулю» эквивалентна двум выражениям:

1. «результат истинен (равен 1), если A не равно B (A≠B)»;
2. «если A не равно B (A≠B), то истина (1)».

Часто указывают на сходство между сложением по модулю 2 и конструкцией «либо … либо …» в естественном языке. Составное утверждение «либо A, либо B» считается истинным, когда истинно либо A, либо B, но не оба сразу; в противном случае составное утверждение ложно. Это в точности соответствует определению операции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как {\displaystyle 0}.

Эту операцию нередко сравнивают с дизъюнкцией потому, что они очень похожи по свойствам, и обе имеют сходство с союзом «или» в повседневной речи. Сравните правила для этих операций:

1. A∨B{\displaystyle A\lor B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, или оба сразу («хотя бы один из двух»).
2. A⊕B{\displaystyle A\oplus B} истинно, если истинно A{\displaystyle A} или B{\displaystyle B}, но не оба сразу («только один из двух»).

Операция ⊕{\displaystyle \oplus }исключает последний вариант («оба сразу») и по этой причине называется исключающим «ИЛИ».
Операция ∨{\displaystyle \lor }включает последний вариант («оба сразу») и по этой причине иногда называется включающим «ИЛИ».Неоднозначность естественного языка заключается в том, что союз «или» может применяться в обоих случаях.

Основные логические операции

Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.

Логическое отрицание (инверсия) —НЕ

Данная операция используется при обозначении отрицания. Она обозначается знаками — NO, NOT, ! В=2 (истина), а после выполнения операции отрицания, В, к примеру, приобретет значение 1 (ложное).

Таблица истинности инверсии:

Результаты операции НЕ следующие:

• если исходное выражение истинно, то результат его отрицания будет ложным;

• если исходное выражение ложно, то результат его отрицания будет истинным. 

Логическое сложение (дизъюнкция, объединение) — ИЛИ

Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |. 

Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.

Таблица истинности операции ИЛИ:

Логическое умножение(конъюнкция) — И

В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.

За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице). 

При всех остальных значениях операция будет ложной.

Таблица истинности операции И приведена ниже:

Логическое следование (импликация) — ЕСЛИ ТО

Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если…, то».

Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if…then.

Таблица истинности операции ЕСЛИ ТО выглядит так:

Операция эквивалентности (равнозначности) — А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В

Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.

И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.

Таблица истинности операции эквивалентности:

Стрелка Пирса

Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.

Обозначения: $\downarrow$ , ИЛИ-НЕ

Таблица истинности для стрелки Пирса

Рисунок 7.

Свойства:

Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:

$X \downarrow X = ¬X$— отрицание

$(X \downarrow Y) \downarrow (X \downarrow Y) \equiv X \vee Y$ — дизъюнкция

$(X \downarrow X) \downarrow (Y \downarrow Y) \equiv X \wedge Y$ — конъюнкция

$((X \downarrow X) \downarrow Y) \downarrow ((X \downarrow X) \downarrow Y) = X \to Y$ — импликация

В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).

Примеры решений

В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).

Решать задание нужно по такому алгоритму:

1. Упрощение выражения: S|T|T&S|¬(T&S).
2. Порядок операций: первая — ¬(T&S), вторая — T&S, третья — совокупность первой и второй, четвертая — включает третью и один элемент, стоящий впереди и пятая — к полученному результату в четвертой прибавить первый элемент.
3. Составление таблицы:

T	S	¬(T&S)	T&S	|	S|T|	Результат
T	F	T	T	T
1	T	F	T	T	T
1	T	F	T	T	T
1	1	T	T	T	T

Следующий пример будет сложнее, поскольку выражение ¬ { ¬& ¬(S&S) } следует упростить, а затем составить таблицу. Задача решается по такой методике:

1. Упрощение: ¬{ ¬& ¬(S&S)}=¬{ ¬&¬(S)}=1&S.
2. Составление таблицы:

S	1&S
O	FALSE
1	TRUE

Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.

Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.

Виды выражений

С помощью логических операций можно строить теории, а также решать сложные задачи, результатом которых окажется справедливый итог. Стоит помнить о том, что прослеживать имеющиеся связи для анализа необходимо крайне внимательно. А еще – учитывать заданные условия, которые относятся к поставленной задаче.

Логические выражения могут быть:

• простыми;
• сложными.

В первом случае результатом обработки заданной операции выступать только «истина» или «ложь». Во втором – или итогом становятся или только истинные операции, или исключительно ложные.

Процедуры получения сложного выражения из нескольких простых имеют определенное название. А именно – формулы логического характера.

Программирование

В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++/Perl/PHP логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|». В языках Pascal/Delphi оба вида дизъюнкции обозначаются с использованием ключевого слова «or», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата \displaystyle{ false } или \displaystyle{ true }. Например:

if (a || b)
{
    /* какие-то действия */
};

Результат будет равен \displaystyle{ false }, если оба операнда равны \displaystyle{ false } или \displaystyle{ 0 }. В любом другом случае результат будет равен \displaystyle{ true }.

При этом применяется стандартное соглашение: если значение левого операнда равно \displaystyle{ true }, то значение правого операнда не вычисляется (вместо \displaystyle{ b } может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

{$B-}

или выключающую

{$B+}

подобное поведение. Например, если левый операнд проверяет необходимость вычисления правого операнда:

if (a == NULL || a->x == 0)
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдёт разыменования нулевого указателя.

Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	\displaystyle{ 01100101_2 }
b =	\displaystyle{ 00101001_2 }
то
a ИЛИ b =	\displaystyle{ 01101101_2 }

Законы алгебры логики

Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.

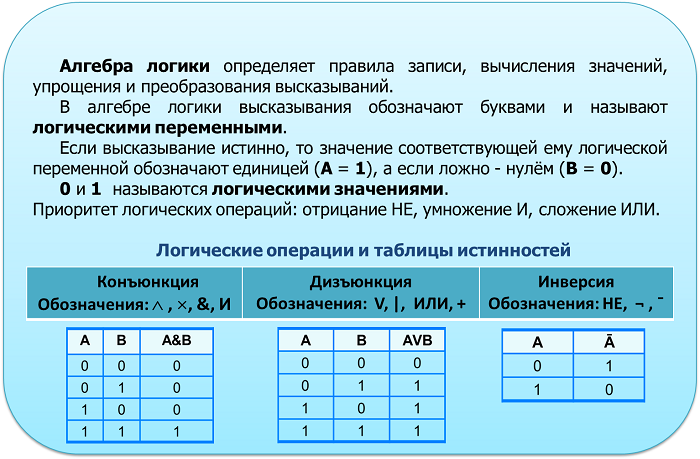
Переместительный закон — предназначен для процесса сложения и вычитания. Суть данного правила в том, что обозначения А и В в операциях дизъюнкции и конъюнкции можно менять.

Сочетательный закон — применяется, когда есть или только операция дизъюнкции, или только операция конъюнкции. Тогда можно обходиться без скобок или хаотично ставить скобки.

Распределительный закон — имеется два типа данного правила: дистрибутивность дизъюнкции относительно конъюнкции и дистрибутивность конъюнкции относительно дизъюнкции. Первый тип схож с дистрибутивным законом алгебры, а второй — нет, поэтому его нужно доказывать.

Закон двойственности и инверсии (закон Моргана) — основоположником данного правила стал шотландский математик и логик де Морган. Он разработал правило, которое связывает логические операции конъюкцию (И) и дизъюнкцию (ИЛИ) с помощью отрицания.

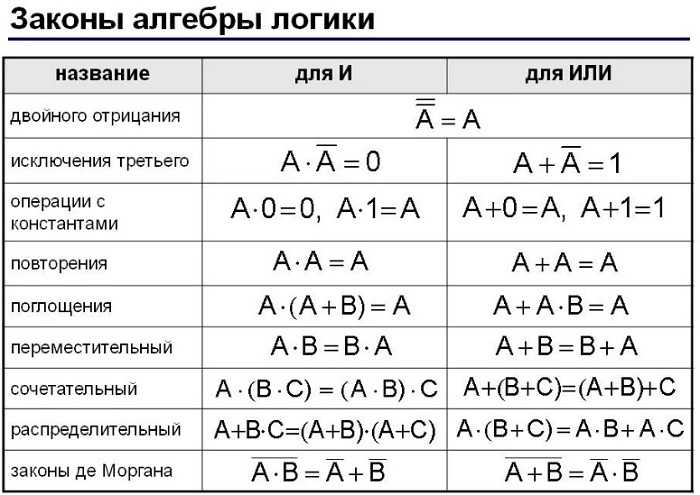
Основные законы алгебры логики представлены в таблице:

Программирование

В языках C/C++, Java, C#, Ruby, PHP, JavaScript, Python и т. д. битовая операция поразрядного дополнения обозначается символом «^», в языках Паскаль, Delphi, Ada, Visual Basic — зарезервированным словом xor, в языке ассемблера — одноимённой логической командой. При этом сложение по модулю 2 выполняется для всех битов левого и правого операнда попарно. Например,

если

a=011001012{\displaystyle a=01100101_{2}}

b=001010012{\displaystyle b=00101001_{2}}

то

a ^b=010011002{\displaystyle a{\hat {\ }}b=01001100_{2}}

Выполнение операции исключающее «или» для значений логического типа (true, false) производится в разных языках программирования по-разному. Например, в Delphi используется встроенный оператор XOR (пример: условие1 xor условие2). В языке C, начиная со стандарта C99, оператор «^» над операндами логического типа возвращает результат применения логической операции XOR. В С++ оператор «^» для логического типа bool возвращает результат согласно описанным правилам, для остальных же типов производится его побитовое применение.

Использование побитового исключающего «или» позволяет поменять местами значения целых переменных без использования дополнительной памяти.

Операторы сравнения

Для формирования логических условий применяются соответствующие знаки. К ним относятся следующие: более (>), менее (<), более либо равно (>=), менее или равно (<=), равно (==) и не равно (==!). Чтобы понять их смысловое значение, нужно разобрать примеры на практике:

1. >: 5>4.
2. <: 3<9.
3. >=: 5>=5 и 6>=8.
4. <=: 3<=3 и 6<=11.
5. <> <>

Следует отметить, что в этих примерах получается истинное значение, поскольку условие выполняется. Однако в информатике при построении алгоритмов используются методы ветвления. Они представляют собой такую конструкцию: ЕСЛИ (a>b), ТО a+b. ИНАЧЕ (a*b). Читается запись следующим образом: в том случае, когда значение а больше b, нужно сложить оба числа, а иначе (a<b) — их перемножить.

Булева алгебра

Логическая функция MAX в двухзначной (двоичной) логике называется дизъюнкция (логи́ческое «ИЛИ», логи́ческое сложе́ние или просто «ИЛИ»). При этом результат равен наибольшему операнду.

В булевой алгебре дизъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Таким образом, результат равен {\displaystyle 0}, если все операнды равны {\displaystyle 0}; во всех остальных случаях результат равен 1{\displaystyle 1}.

Таблица истинности
a{\displaystyle a}	b{\displaystyle b}	a∨b{\displaystyle a\lor b}
{\displaystyle 0}	{\displaystyle 0}	{\displaystyle 0}
{\displaystyle 0}	1{\displaystyle 1}	1{\displaystyle 1}
1{\displaystyle 1}	{\displaystyle 0}	1{\displaystyle 1}
1{\displaystyle 1}	1{\displaystyle 1}	1{\displaystyle 1}

Таблица истинности для тернарной (трёхоперандной) дизъюнкции:

a{\displaystyle a}	b{\displaystyle b}	c{\displaystyle c}	a∨b∨c{\displaystyle a\lor b\lor c}
1	1
1	1
1	1	1
1	1
1	1	1
1	1	1
1	1	1	1

Условное суждение или импликация (от лат. implico – тесно связываю).

Передавая условие в естественном языке, мы начинаем со слова «если», поэтому в импликации используется союз если…, то… .

Обозначается знаком «→».

Схема суждения: «а → в». Читается: «если А, то В».

Например: «Если перерезать провод, то лампа погаснет».

Первое суждение (основание) «Провод перерезали», второе(следствие) – «Лампа погасла».

Суждение «а» называется основание или антецендент (от лат. antecedens – предшествующий, предыдущий), суждение «в» – следствие или консеквент (от лат. concequens – следствие).

Двойная импликация или эквиваленция

Используется союз если и только если…, то… (тогда и только тогда, когда…).

Например: «Если студент сдал все зачеты и экзамены, то может быть переведен на следующий курс».

Эквиваленция обозначается знаком «».

Схема: «а в». Читается: «если, и только если А, то В».

Разница между импликацией и эквиваленцией:

• Если в импликации поменять местами основание и следствие, суждение перестанет быть истинным, станет только вероятным. Например: «Если мотор заглох, то машина не поедет» – истинное суждение. Напротив, суждение «Если машина не едет, значит, мотор заглох» является только вероятным.
• В эквиваленции перестановка основания и следствия не ведет к изменению значения суждения. Например: «Если субъект и предикат общеутвердительного суждения совпадают по объему, то оба термина распределены» так же верно, как и суждение «Если субъект и предикат общеутвердительного суждения распределены, то их объемы совпадают». Эквивалентные суждения являются равнозначными.

Следует отметить, что если в конъюнкции, слабой и строгой дизъюнкциях может быть больше чем два члена суждения, то в импликации и эквиваленции их может быть только два.

Классическая логика

В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для дизъюнкции:

• a→a∨b{\displaystyle a\to a\lor b}
• b→a∨b{\displaystyle b\to a\lor b}
• (a→c)→((b→c)→((a∨b)→c)){\displaystyle (a\to c)\to ((b\to c)\to ((a\lor b)\to c))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции

Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.