Алгоритм

Свойства алгоритмов

Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.

Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.

Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.

Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.

Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.

Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.

Главные характеристики

Выделяют следующие свойства алгоритма: массовость, дискретность, результативность, определенность, понятность, формальность, завершаемость. Будет не лишним рассмотреть их более подробно, дав каждому свойству алгоритма пояснение:
1. Массовость (универсальность). Благодаря этому свойству, алгоритм можно успешно применять к различным наборам исходных данных. Пусть существует запись некой абстрактной последовательности, выраженная формулой. Подставляя в эту формулу значения (каждый раз новые), пользователь будет получать верные решения в соответствии с определенным алгоритмом действий.
2. Дискретность (разрывность). Это свойство характеризует структуру. Каждая алгоритмическая последовательность действий делится на этапы (шаги), а процесс решения задачи — это последовательное исполнение простых шагов. Также дискретность обозначает, что для выполнения каждого этапа потребуется конечный временной отрезок (исходные данные преобразуются во времени в результат дискретно).
3. Определенность (точность, детерминированность) — это свойство указывает алгоритму, что каждый его шаг должен быть строго определенным, то есть различные толкования должны быть исключены. Строго определяется и порядок выполнения шагов. В результате каждый шаг определяется состоянием системы однозначно, когда четко понятно, какая команда станет выполняться на следующем шаге. Как итог — при любом исполнителе для одних и тех же исходных данных при выполнении одной и той же цепочки команд будет выдаваться одинаковый результат. Да, существуют вероятностные алгоритмы — в них на последующий шаг влияют как текущее состояние системы, так и генерируемое случайное число. Но при включении способа генерации рандомных чисел в перечень «исходных данных», вероятностный алгоритм превращается в подвид обычного.
4. Понятность. Должны быть включены лишь те команды, которые доступны и понятны исполнителю, то есть входят в систему его команд.
5. Формальность. Любой исполнитель действует формально и лишь выполняет инструкции, не вникая в смысл. Он не отвлекается от поставленной задачи и не рассуждает, зачем и почему они нужны. Рассуждениями занимается разработчик алгоритма, задача же исполнителя — просто исполнить предложенные команды и получить результат. «Приказы не обсуждают, а выполняют».
6. Завершаемость (конечность). Если исходные данные заданы корректно, алгоритм завершит свое действие и выдаст результат за конечное число шагов.
7. Результативность. Согласно этому свойству, любой алгоритм должен завершаться конкретными результатами.

Сложность алгоритма

Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.

Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.

Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.

•  O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
•  O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
•  O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
•  O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
•  O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.

Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.

Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.

O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.

Свойства и виды

Для изучения понятия нужно разобраться в свойствах алгоритма в информатике. Их существует несколько:

• дискретность;
• детерминированность или определенность;
• понятность;
• завершаемость или конечность;
• массовость или универсальность;
• результативность.

Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задания в виде выполнения простых шагов. При этом на пункты отводится определенное количество времени. Каждый шаг должен определяться состоянием системы, то есть при одних и тех же исходных данных результат не меняется. Но есть и вероятностные алгоритмы, где пункты зависят от системы и случайно генерируемых чисел. В этой ситуации понятие становится подвидом обычного.

Понятность заключается в том, что команды алгоритма должны быть доступны конкретному исполнителю и входить в его личную систему. В ходе работы математическая функция при правильно заданных исходных данных выдает результат за определенное количество шагов. Иногда процедура может не завершиться, но вероятность таких случаев стремится к нулю.

У каждого алгоритма есть свои начальные условия, цели и пути решения задачи. Существует большая разница между вычислительными и интерактивными видами. Происхождение первых связано с опытами ученого Тьюринга, они могут преобразовать входные данные в выходные. Вторые предназначены для связи с объектом управления, они работают только под внешним воздействием. Ученые выделяют несколько видов алгоритмов в информатике:

• детерминированные или жесткие;
• гибкие;
• линейные;
• разветвляющиеся;
• циклические;
• вспомогательные;
• структурные блок-схемы.

Жесткие еще называются механическими, так как чаще всего они используются для работы двигателя или машины. Они задают действия в единственно верной последовательности, что приводит к искомому или требуемому результату при условии выполнения процессов, для которых они и разработаны.

Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются при различных умственных выводах без строгих аргументов, а вторые дают возможность получить один результат несколькими способами.

Линейный тип — это набор команд, которые выполняются в строгой последовательности. Разветвляющийся включает хотя бы одно условие и при проверке дает разделение на несколько блоков. Появляются альтернативные ветвления программы.

В циклических видах несколько раз повторяются одни и те же действия, при этом меняются исходные данные. Сюда относятся переборы вариантов и бо́льшая часть способов расчета. Циклом в этом случае называют последовательность команд, которые нужно выполнить множество раз для достижения требуемого результата.

Подчиненный или вспомогательный вид является ранее разработанным алгоритмом для быстрого решения задачи. Он необходим для сокращения записи, если в структуре есть одинаковые команды. Схемами называются графические изображения с помощью блоков и соединяющих их прямых линий. Их используют перед программированием в качестве наглядных примеров, поскольку зрительное восприятие позволяет быстрее осмыслить процесс обработки информации и выявить возможные ошибки. В блоках отображаются исходные данные, которые вносятся в компьютер для вычислений.

Правила составления блок-схемы

Чтобы составить блок-схему алгоритма грамотно, необходимо следовать приведенным ниже принципам.

• Начало и конец схемы обязательно ограничиваются соответствующими блоками в одном экземпляре.
• Начальный блок должен быть соединен с конечным линиями связи.
• Линии потока необходимо рисовать из всех блоков, кроме конечного.
• Все блоки нумеруются по порядку слева направо и сверху вниз. Номера ставятся в верхнем левом углу с разрывом начертания.
• Между всеми блоками обеспечивается взаимная связь через линии, определяющие последовательность выполнения команд. Движение потока в обратном порядке от принятого по умолчанию обязательно обозначается стрелками.
• Используемые в схеме линии могут быть входящими или выходящими. Это разделение относительное. Для одного линия, выходящая из одного блока, для другого уже будет являться входящей.
• Начальный блок имеет лишь выходящие линии потока. Соответственно, в конечный блок линии могут только входить.
• Поскольку движение потока идет сверху вниз, входящие линии принято изображать сверху от блока, а выходящие — снизу. Это в целом упрощает чтение блок-схемы.
• Линии потока могут обрываться. При этом места разрывов необходимо помечать специальными соединительными элементами.
• Чтобы блок-схема легче читалась, допускается описательную часть выносить в комментарии.

Правила составления блок-схемы

Виды алгоритмов и примеры

По конструкции алгоритмы можно разделить на несколько групп.

Линейные алгоритмы

В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.

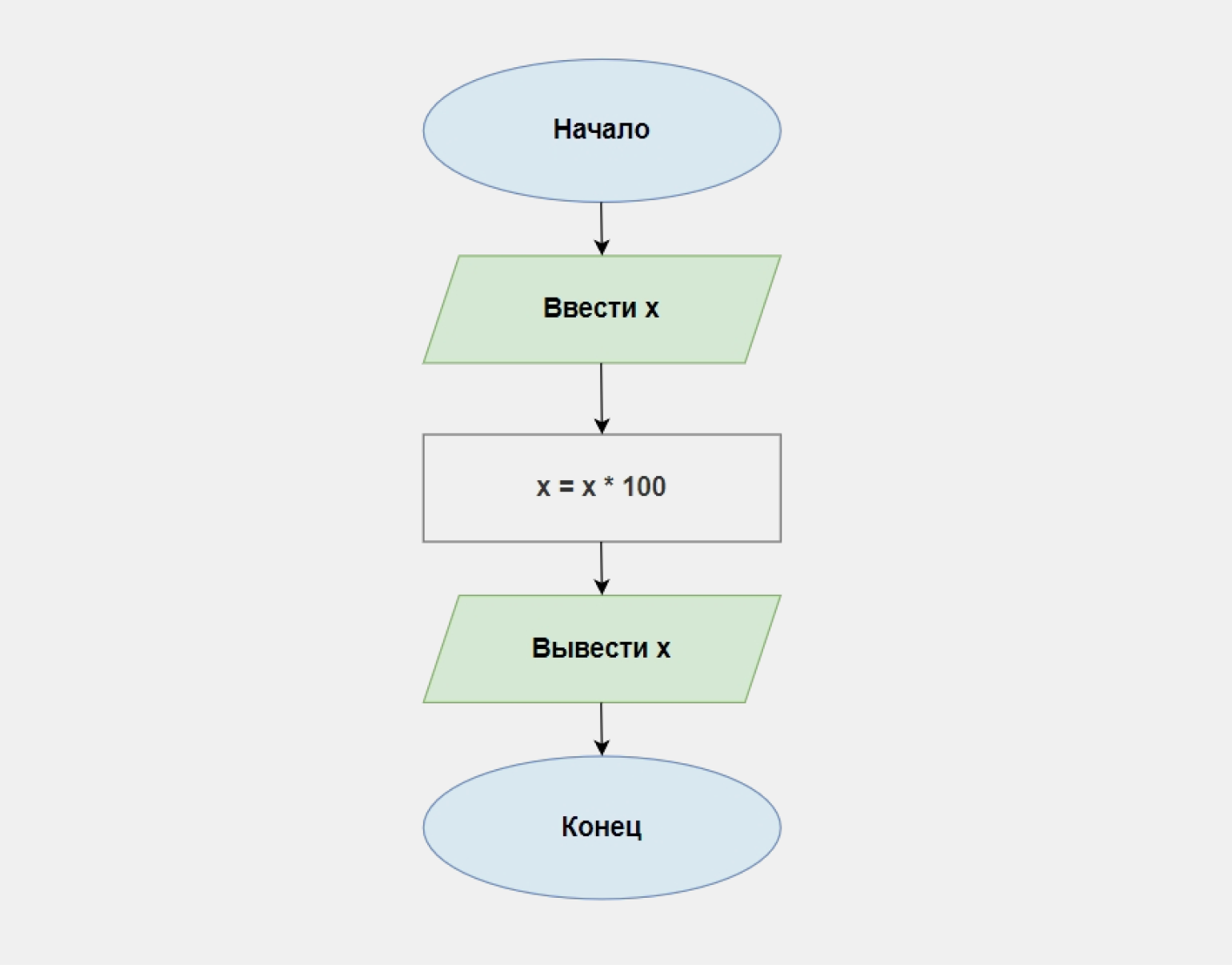
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.

Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:

Изображение: Skillbox Media

Ниже приведена реализация алгоритма на языке Python:

Ветвящиеся алгоритмы

В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).

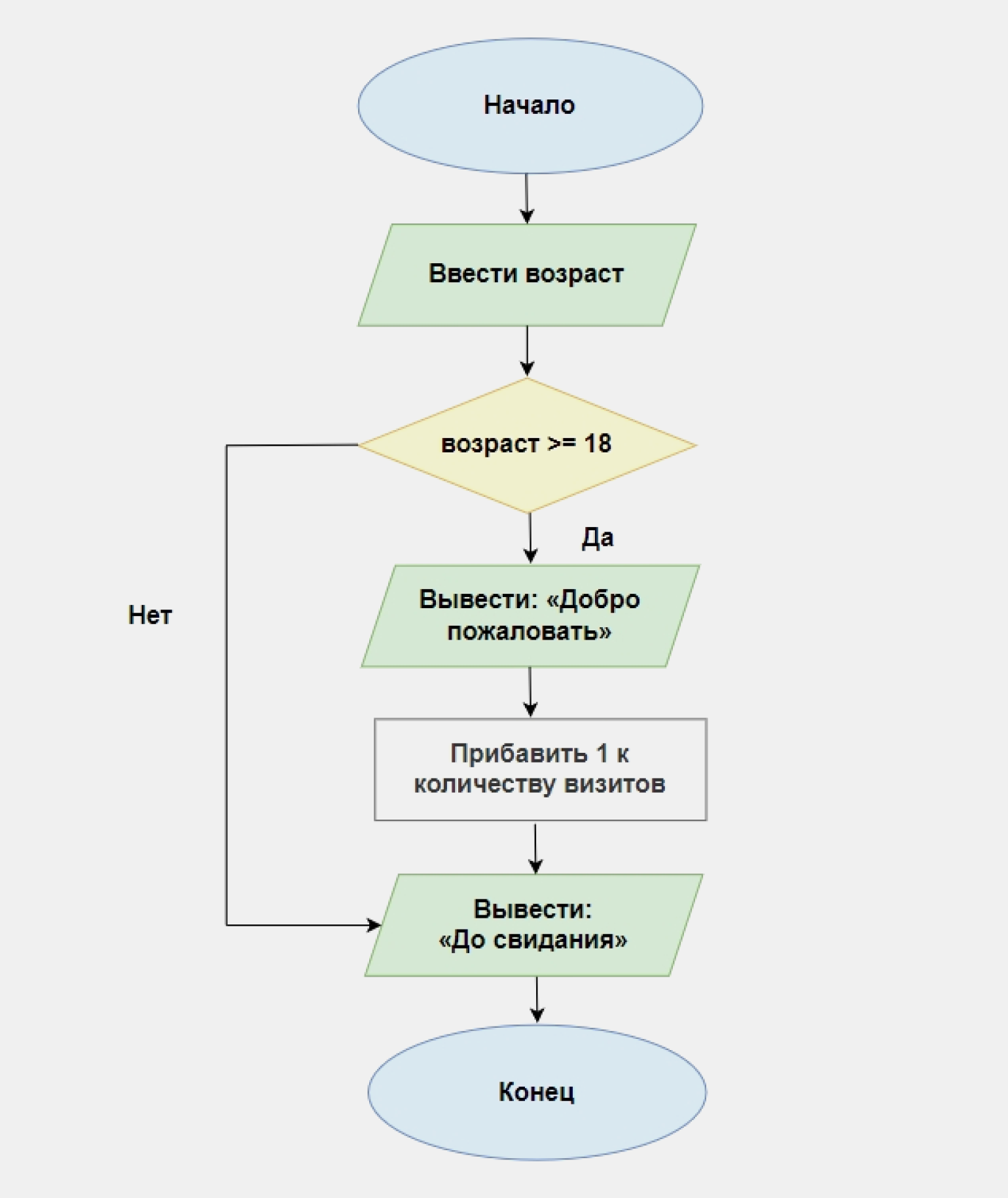
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.

Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:

Изображение: Skillbox Media

То же самое на Python:

Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.

Циклические алгоритмы

Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.

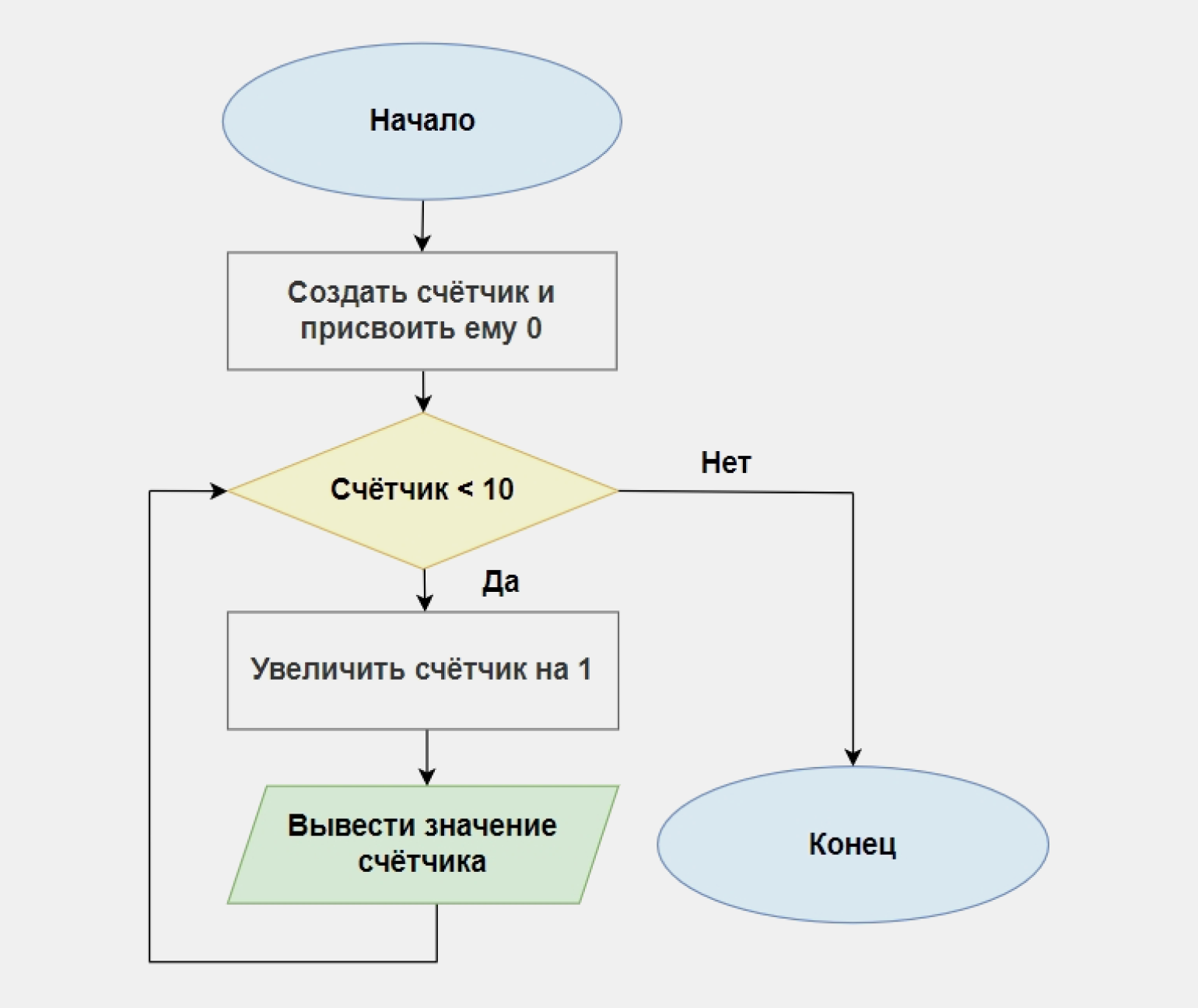
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.

В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:

Изображение: Skillbox Media

Переведём это в код на Python

Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:. Результат работы программы:

Результат работы программы:

Рекурсивные алгоритмы

Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.

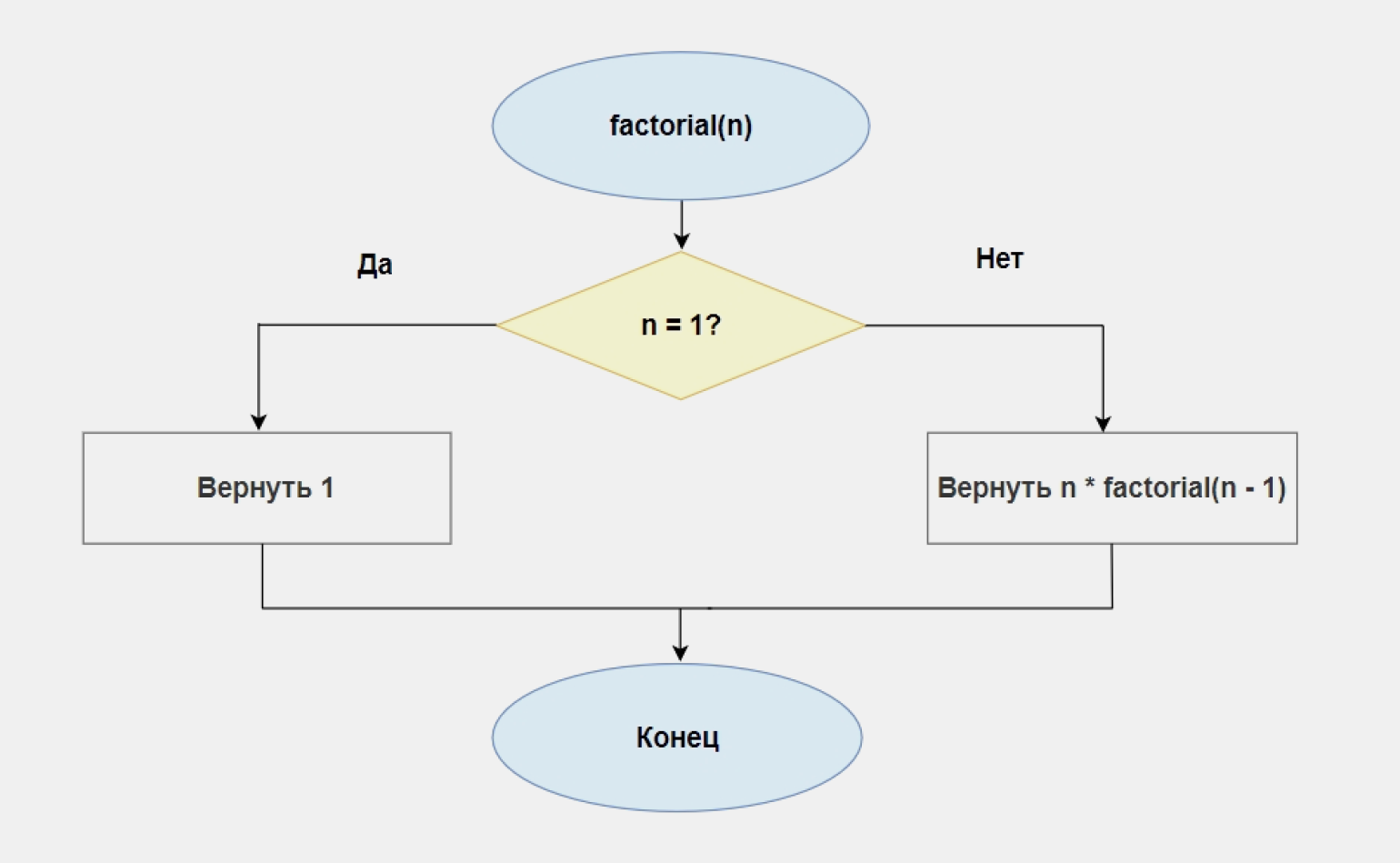
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.

Вот как выглядит блок-схема рекурсивного алгоритма:

Изображение: Skillbox Media

На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.

Корректные и некорректные алгоритмы

Мы называем алгоритм корректным, если на каждый получаемый ввод он делает правильный вывод. Алгоритм считается некорректным, если хотя бы один ввод приводит к неправильному выводу.

Остановитесь и подумайте:Каково минимальное количество монет номиналами $(25, 20, 10, 5, 1)$, необходимое для сдачи в $40$ центов?

— это некорректный алгоритм! Представьте сдачу в 40 центов, выданную в номиналах $c_1 = 25$, $c_2 = 20$, $c_3 = 10$, $c_4 = 5$ и $c_5 = 1$. привел бы к неправильному результату: он выдал бы 1 четвертак (25 центов), 1 дайм (10 центов) и 1 никель (5 центов) вместо 2 монет по двадцать центов. Хоть это и может выглядеть надуманно, в 1875 году в США существовала монета в двадцать центов. Насколько мы можем быть уверены, что выдаст минимальное количество монет в современных номиналах Соединенных Штатов или любой другой страны?

Чтобы исправить алгоритм , нам нужно рассмотреть все возможные комбинации монет с номиналами $c_1, c_2, \dotsc , c_d$, которые дают в сумме $money$, и выдать комбинацию с минимальным количеством монет. Мы рассматриваем только комбинации, в которых $i_1 \le money/c_1$ и $i_2 \le money/c_2$ (в целом, величина $i_k$ не должна превышать $money/c_k$), в ином случае мы вернем большее количество денег, чем $money$. В псевдокоде, приведенном ниже, используется символ $\sum$. Он обозначает суммирование: $\sum^m_{i=1} a_i = a_1 + a_2 + \dotsm + a_m$. Псевдокод также использует концепт «бесконечность» (обозначается $\infty$) в качестве начального значения для $smallestNumberOfCoins$. Реализация описанного подхода на реальных языках программирования может различаться, но сейчас подробности для нас не важны.

Вторая строка повторяется с каждой возможной комбинацией $(i_1, \dotsc, i_d)$ из $d$ индексов и останавливается, когда достигает

$$
\left(\frac{money}{c_1}, \dotsc, \frac{money}{c_d}\right),
$$

Как мы можем узнать, что не содержит ту же проблему, что и , — неверный результат при каком-то вводе? Раз рассматривает все возможные комбинации номиналов, рано или поздно алгоритм придёт к оптимальному решению и запишет его в массив $change$. В любой комбинации монет, которая даёт в сумме $M$, должно быть как минимум столько же монет, сколько и в оптимальной. Таким образом, никогда не завершит работу с неоптимальным набором $change$.

На данный момент мы ответили только на один из двух важных вопросов об алгоритмах: «Работает ли он?». Однако мы не ответили на вопрос: «Сколько времени занимает выполнение?».

Остановитесь и подумайте:Сколько примерно итераций цикла выполняет ?

• money
• $money^d$
• $d$

Что такое алгоритм?

Понятие алгоритма такое же основополагающее для информатики, как и понятие информации

Именно поэтому важно в нем разобраться.. Название «алгоритм» произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в
783—850 гг

В своей книге «Об индийском счете» он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними «столбиком», знакомые теперь каждому школьнику. В
XII веке эта книга была переведена на латынь и получила широкое распространение в Европе.

Название «алгоритм» произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса ал-Хорезми (Alhorithmi), жившего в
783—850 гг. В своей книге «Об индийском счете» он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними «столбиком», знакомые теперь каждому школьнику. В
XII веке эта книга была переведена на латынь и получила широкое распространение в Европе.

Человек ежедневно встречается с необходимостью следовать тем или иным правилам, выполнять различные инструкции и указания. Например, переходя через дорогу на перекрестке без светофора надо
сначала посмотреть направо. Если машин нет, то перейти полдороги, а если машины есть, ждать, пока они пройдут, затем перейти полдороги. После этого посмотреть налево и, если машин нет, то перейти
дорогу до конца, а если машины есть, ждать, пока они пройдут, а затем перейти дорогу до конца.

В математике для решения типовых задач мы используем определенные правила, описывающие последовательности действий. Например, правила сложения дробных чисел, решения квадратных уравнений и
т. д. Обычно любые инструкции и правила представляют собой последовательность действий, которые необходимо выполнить в определенном порядке. Для решения задачи надо знать, что дано, что следует
получить и какие действия и в каком порядке следует для этого выполнить. Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, и есть
алгоритм.

Алгоpитм — заранее заданное понятное и точное пpедписание возможному исполнителю совеpшить определенную последовательность действий для получения решения задачи за конечное число шагов.

Это — не определение в математическом смысле слова, а, скорее, описание интуитивного понятия алгоритма, раскрывающее его сущность.

Понятие алгоритма является не только одним из главных понятий математики, но одним из главных понятий современной науки. Более того, с наступлением эры информатики алгоритмы становятся
одним из важнейших факторов цивилизации .

Понятие алгоритма[править]

Понятие алгоритма — одно из основных в программировании и информатике. Это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм должен описываться на формальном языке, исключающем неоднозначность толкования. Исполнитель может быть человеком или машиной. Исполнитель должен уметь выполнять все команды, составляющие алгоритм. Множество возможных команд конечно и изначально строго задано. Действия, выполняемые по этим командам, называются элементарными.

Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.

Приведём для примера простой алгоритм действия пешехода, который
позволит ему безопасно перейти улицу:

1. Подойти к дороге.
2. Дождаться зелёного сигнала светофора.
3. Перейти дорогу.
4. Если впереди есть ещё одна дорога, то перейти к шагу 1.

Алгоритмы обладают свойством детерминированности (определённости): каждый шаг и переход от шага к шагу должны быть точно определены так, чтобы его мог выполнить любой другой человек или механическое устройство.

Кроме детерминированности, алгоритмы также должны обладать свойством конечности и массовости:

Конечность

Алгоритм всегда должен заканчиваться за конечное число шагов, но это число не ограничено сверху.

Массовость

Алгоритм применяется к некоторому классу входных данных (чисел, пар чисел, набору букв и тому подобному). Не имеет смысла строить алгоритм нахождения наибольшего общего делителя только для одной пары чисел 10 и 15.

Поясним эти свойства на простом примере. Рассмотрим следующую формулу вычисления числа π\pi:
π=4(1−13+15−17+…)=4∑i=∞(−1)i2i+1\pi =4\left(1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\dots \right)=4\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{2i+1}}.

Является ли эта формула алгоритмом вычисления числа π\pi? Ответ на этот вопрос — «нет», так как здесь нет ни свойства массовости (нет входных данных), ни свойства конечности (сумма бесконечного количества чисел).

Операция суммирования бесконечного ряда не является элементарной ни для современных компьютеров, ни для человека, а если разложить эту операцию на отдельные шаги сложения, то получим бесконечное число шагов. Алгоритмы же по определению должны выполняться за конечное число шагов и через конечное число шагов предоставлять результат вычислений.

Примеры простых алгоритмических задач[править]

Здесь мы сформулируем несколько простых алгоритмических задач, которые полезно прорешать, чтобы освоится с понятием алгоритма.

Задача 5

Сколько раз в рекурсивном алгоритме вычисления будет вызвана процедура вычисления ?

Задача 6

Сколько раз в рекурсивном алгоритме вычисления будет вызвана процедура вычисления ?

Задача 7

Продолжите ряд FnF_{n} на отрицательные значения n. Измените рекурсивный алгоритм вычисления так, чтобы он работал и при отрицательных .

Задача 8

Разработайте алгоритм вычисления числа F1000F_{1000} и реализуйте его в виде программы на языке Паскаль, Си или любом другом языке программирования. Сколько цифр в десятичной записи этого числа?

Задача 9

Напишите рекурсивный алгоритм вычисления n!=1⋅2⋅⋯⋅nn!=1\cdot 2\cdot \dots \cdot n на псевдокоде.

Задача 10

Используя соотношение НОД(a,b)=(a,\;b)=\;НОД(amodb,b)(a\;{\bmod {\;}}b,b), напишите рекурсивный алгоритм, вычисляющий НОД двух чисел aa и bb.

Задача 11

Напишите алгоритм, который получает на вход чило nn и выводит слово «Простое», если это число простое (делится только на себя и на единицу), а иначе — слово «Составное». Попробуйте написать алгоритм, время работы которого ограничено функцией CnC{\sqrt {n}}, где CC — некоторая константа.

Задача 12

Дана рекуррентная последовательность an=2⋅an−1−an−2+1a_{n}=2\cdot a_{n-1}-a_{n-2}+1, a=a1=1a_{0}=a_{1}=1. Напишите рекурсивный и нерекурсивный алгоритмы вычисления nn-го элемента этой последовательности. Найдите явную формулу члена этой последовательности (рассмотрите последовательность разностей соседних элементов).

Задача 13

Квадратный бумажный лист сложили пополам по вертикали (так, что изгиб шёл посредине, сверху вниз) (1-я операция), потом по горизонтали (2-я операция), затем снова по вертикали (3-я операция) и так далее, сделав всего nn операций. Затем сделали разрез по горизонтали. Напишите рекурсивный алгоритм, вычисляющий
число получившихся бумажек.

Задача 14

Дано множество прямых на плоскости, никакие три из которых не пересекаются в одной точке. Напишите рекурсивный алгоритм (псевдокод) закраски получившихся многоугольников в чёрный и белый цвета так, чтобы многоугольники одного цвета не имели общей стороны.

Задача 15

Рассмотрим следующее рекуррентное соотношение для функции f(n)=an{f(n)=a^{n}}:

a=1,an={an−1⋅a,if n is odd(an2)2⋅a,if n is evena^{0}=1,\;a^{n}=\left\{{\begin{matrix}a^{n-1}\cdot a,&{\mbox{if }}n{\mbox{ is odd}}\\\left(a^{n/2}\right)^{2}\cdot a,&{\mbox{if }}n{\mbox{ is even}}\end{matrix}}\right..

Нарисуйте дерево рекурсивных вызовов для f(1000)f(1000) (подсказка: это дерево не ветвится и выглядит как цепочка вызовов).

Задача 16

Чем отличается алгоритм от функции?

Чем отличается программа от алгоритма?

В чём разница между идеей решения и алгоритмом решения задачи?

Способы записи

Алгоритмы записываются несколькими методами. В информатике используется всего три:

• словесно-формульный;
• графический;
• программный.

В первом случае алгоритм записывается простым языком — словами и математическими формулами, что необходимо для понимания его теории. Здесь учитываются исходные данные, действия с ними и условия получения результата. Второй тип записи — компьютерное описание. Для этого применяются языки программирования и сами программы — форсы представления расчетов для их выполнения машиной.

Графическое описание состоит из связанных между собой географических фигур. Основные элементы блок-схем:

• прямоугольники;
• эллипсы;
• ромбы;
• шестиугольники;
• стрелки;
• пунктирные линии;
• соединительные фигуры.

В прямоугольниках записывают процессы, они указывают на выполнение операций, которые изменяют форму или значение данных. Ромбы содержат способы решения, здесь выбирается следующее направление в зависимости от поставленных условий. Модификации могут передаваться в шестиугольниках, где записываются операции, меняющие команды.

Графическое изображение содержит блоки документов и дисплеев. Оператор может вводить данные с бумаги и выводить их на нее, а также с помощью устройств, которые воспроизводят информацию на экране (проекторы для интерактивных досок, подключенные к компьютерам планшеты и ноутбуки).

Линии и соединительные фигуры указывают на связи между разными блоками и их последовательность. В схеме есть блоки начала и конца алгоритма, его прерывания, которое может произойти из-за сбоев в программе. Можно также указывать комментарии и пояснения исполнителя, для этого есть отдельные фигуры.

Какими свойствами обладают алгоритмы?

Основные свойства алгоритмов следующие:

1.   Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных
данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.

2.   Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс pешения задачи как последовательное выполнение простых (или pанее
опpеделенных) шагов (этапов).

3.   Определенность — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение
алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

4.   Результативность (или конечность) состоит в том, что за конечное число шагов алгоритм либо должен приводить к решению задачи, либо после конечного
числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с
выдачей промежуточных результатов.

5.   Массовость означает, что алгоритм решения задачи разpабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач,
различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

Перейти к параграфам

Ассоциативные контейнеры

Ассоциативные контейнеры сопоставляют ключам некоторые значения. В стандартной библиотеке есть ассоциативные контейнеры, основанные на сбалансированных деревьях поиска и контейнеры, основанные на хеш-таблицах.

Адаптеры и представления

Адаптеры над стандартными контейнерами — это не самостоятельные контейнеры. Они используют какой-нибудь другой последовательный контейнер для хранения своих элементов, но при этом предоставляют свой набор функций для работы с ними. Представления (views) не владеют памятью, а лишь ссылаются на диапазон значений другого контейнера.

Быстрые и медленные алгоритмы

Настоящие компьютеры требуют определенное количество времени на выполнение таких операций, как сложение, вычитание или проверка условий цикла while. Суперкомпьютер может выполнить сложение за $10^{-10}$ секунды, а калькулятор — за $10^{-5}$. Представьте, что у вас есть компьютер, которому требуется $10^{-10}$ секунды на выполнение простой операции (например, сложения), и вы знаете, сколько операций выполняет какой-то конкретный алгоритм. Вы могли бы рассчитать время выполнения алгоритма, просто взяв произведение количества операций и времени, которое занимает одна операция. Однако компьютеры постоянно улучшаются, благодаря чему им требуется меньше времени на операцию. Так, ваше представление о времени выполнения быстро стало бы устаревшим. Вместо того, чтобы рассчитывать время выполнения на каждом компьютере, мы описываем время выполнения через общее количество операций, необходимых алгоритму, — это характеристика самого алгоритма, а не компьютера, который вы используете.

К сожалению, нам не всегда легко определить, сколько операций выполнит алгоритм. Однако если мы можем рассчитать количество базовых операций, выполняемых алгоритмом, то это позволит сравнить его с другим алгоритмом, решающим ту же задачу. Чтобы мучительно не подсчитывать каждое умножение и сложение, можно сравнивать только те участки кода, которые при увеличении размера ввода потребуют больше операций.

Представьте, что алгоритм $A$ выполняет $n^2$ операций при вводе размера $n$, и алгоритм $B$ решает ту же задачу за $3n+2$ операций. Какой алгоритм быстрее: $A$ или $B$? Хотя $A$ и может быть быстрее, чем $B$, при более малом значении $n$ (например, при $n$ между 1 и 3), $B$ будет быстрее при больших значениях $n$ (например, $n >4$). . Так как $f(n)=n^2$ — это, в каком-то смысле, более «быстрорастущая» функция относительно $n$, чем $g(n)=n$. При этом константы 3 и 2 в $3n+2$ не влияют на конкуренцию между двумя алгоритмами при больших значениях $n$. Мы называем $A$ квадратичным алгоритмом и $B$ — линейным

$A$ менее эффективен, чем $B$, потому что он выполняет больше операций для решения задачи, когда значение $n$ большое. Так, иногда мы будем допускать неточности при подсчете операций алгоритма: поведение алгоритма при маленьком вводе неважно

Рассчитаем примерное количество операций, которое потребуется для при вводе из $M$ центов и номиналов $(c_1, c_2, \dotsc, c_d)$. Чтобы рассчитать общее количество операций в цикле for, нам необходимо взять примерное число операций, выполняемое при каждой итерации, и умножить его на общее количество итераций. В нашем случае количество операций можно оценить сверху величиной

$$
\frac{money}{c_1} \times \frac{money}{c_2} \times \dotsm \times \frac{money}{c_d}
$$

Такой тип алгоритмов называется экспоненциальным в противоположность квадратичным, кубическим или другим полиномиальным алгоритмам. Выражение времени выполнения экспоненциального алгоритма использует $n^d$, где $n$ и $d$ — это параметры задачи (например, $n$ и $d$ можно произвольно сделать большими, изменив ввод для алгоритма). Время выполнения полиномиального алгоритма ограничено $n^k$, где $k$ — это константа, не связанная с величиной параметров задачи.

Способы описания алгоритмов

О блок-схеме, как об основном способе представления алгоритмов, мы уже поговорили. Но кроме блоков, есть и другие методы:

1. Словесное описание — это когда структура алгоритма описывается естественным языком. Лучше всего вспомнить любой бытовой прибор (утюг, телевизор, микроволновую печь, холодильник и т. п.). Все эти приборы имеют инструкцию по эксплуатации, то есть перед нами типичное описание алгоритма словами, с учётом которых прибором надо пользоваться. Такой способ не формализован и не учитывает все возможные ситуации, возникающие при эксплуатации. К недостаткам словесного описания относят и неоднозначность толкования некоторых терминов.
   Представьте, что вы куда-то собрались, и вас интересует погода на улице. Словесное описание будет приблизительно таким:
   1) смотрим на градусник, определяем температуру на улице;
   2) если температура ниже 0, надеваем шубу, если выше — куртку.
2. Псевдокод — в этом случае можно говорить о естественном и частично формализованном языке, то есть это описание уже позволяет определить главные этапы решения задачи, что необходимо перед составлением программы — точной записи на языке программирования. Псевдокод характеризуется уже наличием формализованных конструкций и общепринятой математической символикой, однако строгих синтаксических правил по записи не существует.
3. Блок-схема. Схему, состоящую из блоков и линий, включая значения наиболее часто используемых блоков, уже рассмотрели выше. Но вернёмся к нашему примеру с погодой:
4. Программа — описание, созданное на языке алгоритмического программирования. Такой вариант характеризуется высокой степенью формализации, то есть появление программы позволяет решать прикладные задачи. В форме программы описываемый ранее пример будет выглядеть следующим образом: