Длина окружности

Площадь круга

Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан – угольникnправильный   (рис. 1).

Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.

Рис.1

равнаR, – угольника, вписанного в окружность радиуса nПлощадь правильного

, равна1 – угольника, вписанного в окружность радиуса nПлощадь правильного

Следовательно,

Поскольку π, стремится к 1 – угольника, вписанного в окружность радиуса n площадь правильного nпри увеличении , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу   πR2.

Таким образом, площадь круга радиуса R, обозначаемая S, равна

S = πR2.

Дуга окружности

Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360\(\circ\). Тогда половина дуги окружности будет равняться 180. 

При этом дуга, равная 180\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.  

Думаем, хоть раз в жизни вы слышали  фразу “повернуться на 180\(\circ\) градусов” или “поменять свое мнение на 180\(\circ\) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180\(\circ\). 

Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности. 

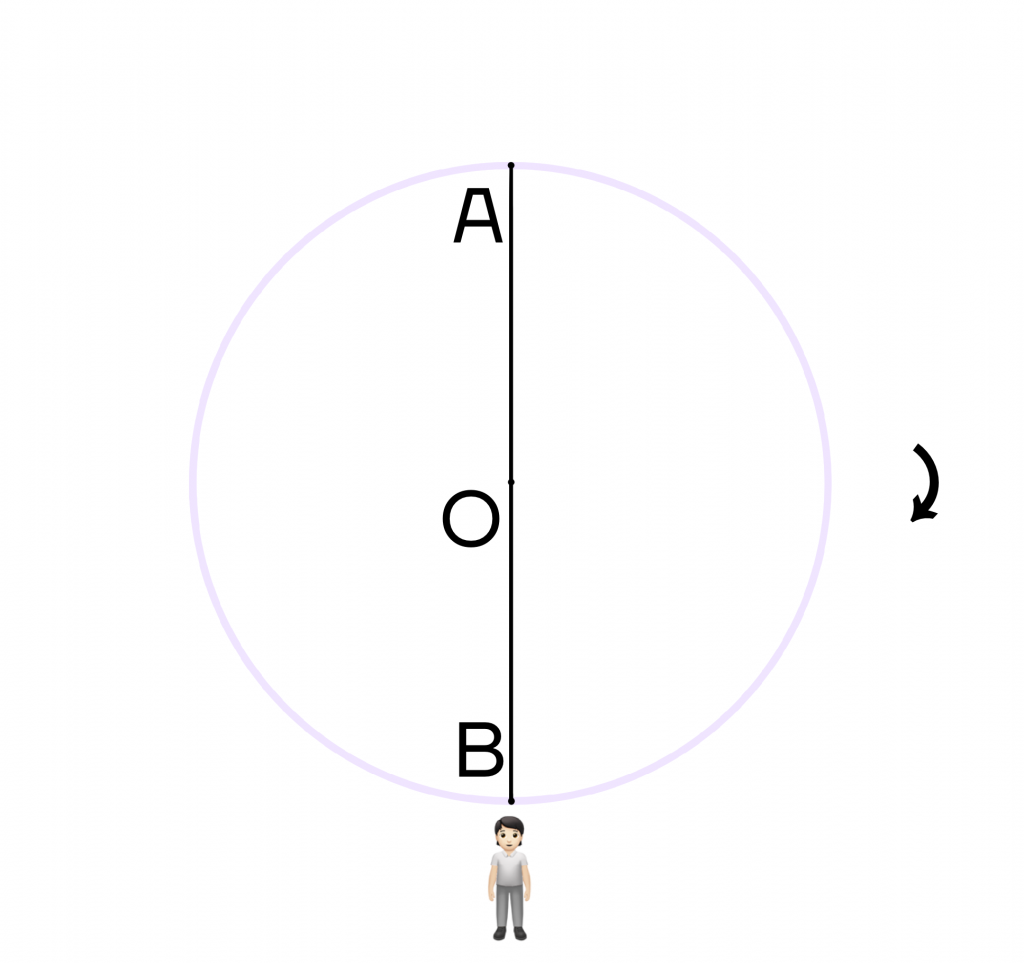
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.

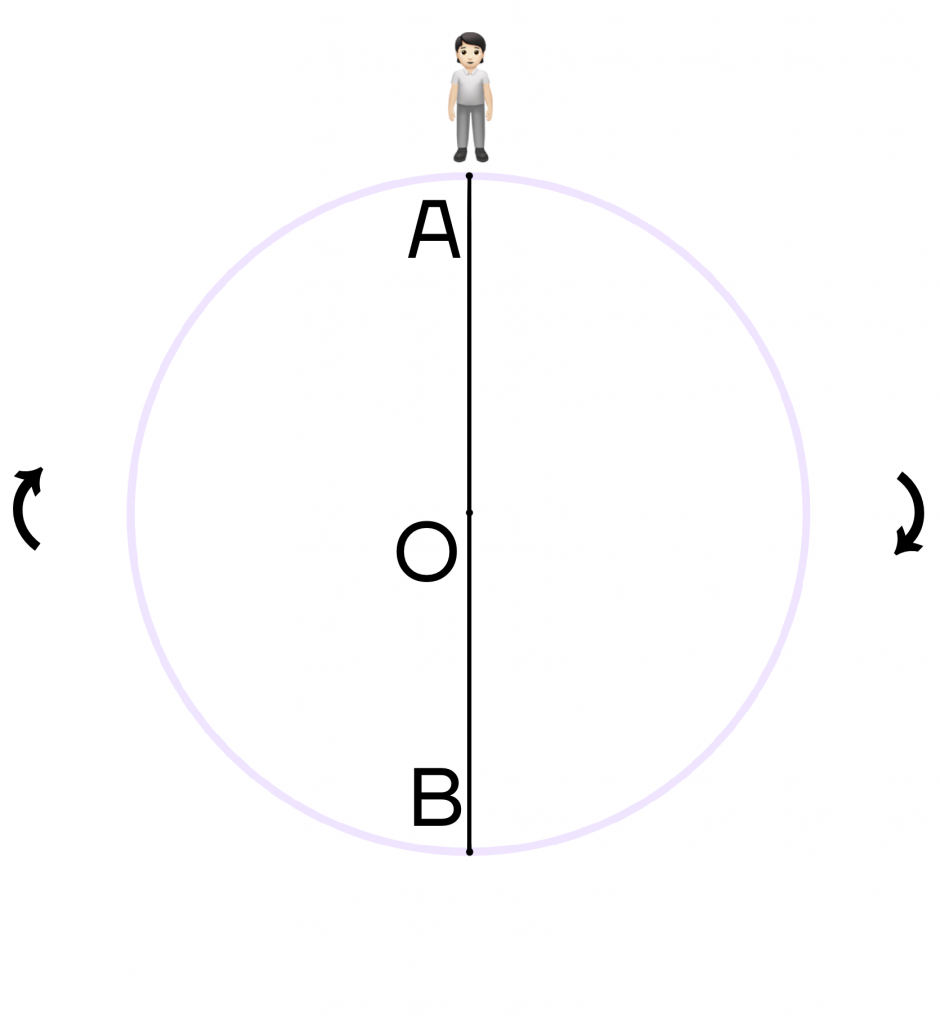
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А. 

Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.

Уравнения[править | править код]

Декартовы координатыправить | править код

Окружность с центральной точкой M=(xM,yM)M = \left(x_M, y_M \right) и радиусом rr описывается следующим уравнением:
(x−xM)2+(y−yM)2=r2\left( x-x_M\right)^2 + \left(y-y_M \right)^2 = r^2
если MM есть начало координат, то уравнение принимает вид:
x2+y2=r2.x^2 + y^2 = r^2.\,
Через три точки на плоскости (x1,y1),(x2,y2),(x3,y3)(x_1,y_1),(x_2,y_2),(x_3,y_3) , не лежащие на одной прямой, всегда можно провести окружность, координаты центра которой определяются формулами:
xM=−12y1(x22+y22−x32−y32)+y2(x32+y32−x12−y12)+y3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2) x_M=-\frac 12 \frac{y_1(x_2^2+y_2^2-x_3^2-y_3^2)+y_2(x_3^2+y_3^2-x_1^2-y_1^2)+y_3(x_1^2+y_1^2-x_2^2-y_2^2)}{x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)}yM=12×1(x22+y22−x32−y32)+x2(x32+y32−x12−y12)+x3(x12+y12−x22−y22)x1(y2−y3)+x2(y3−y1)+x3(y1−y2)
y_M=\frac 12 \frac{x_1(x_2^2+y_2^2-x_3^2-y_3^2)+x_2(x_3^2+y_3^2-x_1^2-y_1^2)+x_3(x_1^2+y_1^2-x_2^2-y_2^2)}{x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)}

Полярные координатыправить | править код

Если полярные координаты центра окружности M=(r,α)M=(r,\alpha), то окружность радиуса rr описывается уравнением:
ρ(φ)=2rcos Косинус (φ−α),\rho(\varphi)=2r\cos (\varphi-\alpha),⩽φ0\leq\varphi
если MM есть начало координат, то уравнение будет иметь вид:
ρ=r.\rho=r.

Комплексная плоскостьправить | править код

На комплексной плоскости окружность задается формулой:
|z−z|=r|z — z_0| = r\,
или в параметрическом виде
Undefined control sequence \Rz_0 + r e^{it},\ t\in\R.

Как графикправить | править код

В декартовой системе координат окружность не является , но она может быть описана как объединение графиков двух следующих функций:
y=yM±r2−(x−xM)2.y = y_M \pm \sqrt{r^2 — (x — x_M )^2}.

если yM=xM=y_M = x_M=0, то функции принимают вид:
y=±r2−x2.y = \pm \sqrt{r^2 — x^2 }.

Параметрическое представлениеправить | править код

Другую возможность описать окружность с помощью декартовых координат даёт параметрическое представление:
x=xM+rcos Косинус φx = x_M + r \cos \varphiy=yM+rsin Синус φy = y_M + r \sin \varphi

здесь координаты xx и yy выражаются через параметр φ\varphi, принимающий все значения, удовлетворяющие неравенству ⩽φ<2π0 \le \varphi < 2 \pi.

Расстояние между центрами окружностей

1. Если две окружности пересекаются в двух точках, расстояние центров меньше суммы и больше разности радиусов.

Действительно, с одной стороны (черт. 104)

OO’ < AO + AO’

с другой

AO + OO’ > AO’

следовательно,

OO’ > AO’ — AO

2. Если две окружности касаются, расстояние центров равно сумме радиусов, если соприкосновение внешнее, и разности радиусов, если соприкосновение внутреннее.

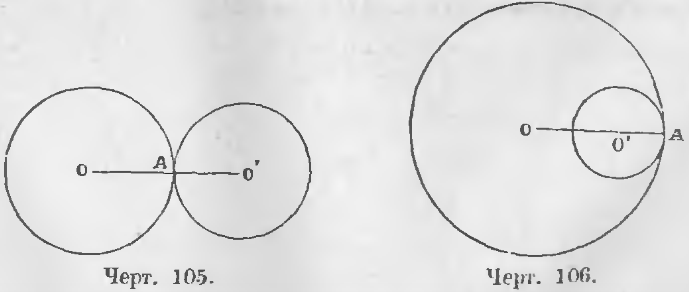
Из чертежа 105 видно, что

OO’ = AO + AO’

а из чертежа 106

OO’ = AO — AO’.

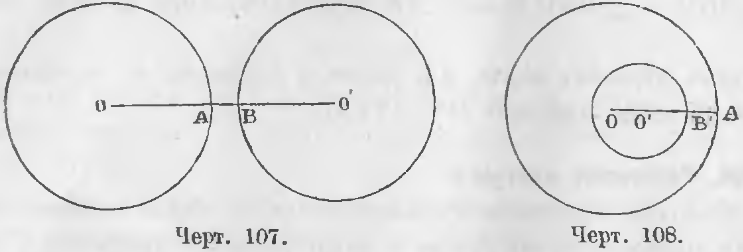
3. Если одна окружность лежит вне другой, расстояние центров больше суммы радиусов.

Из чертежа 107 видно, что

OO’ > AO + BO’

4. Если окружность лежит одна внутри другой, расстояние центров меньше разности радиусов.

Действительно, из чертежа 108 видно, что

OO’ < AO — BO’.

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

l=πd

Подставляем туда известные переменные и получается, что длина окружности равна

l=πd=3,14·5=15,7(см)

Ответ: 15,7 (см)

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен
Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Так и сделаем:

l=2πr=2·π·4≈2·3,14·4=25,12(дм)

Ответ: l=25,12(дм)

Измерение углов

Центральные углы. Углы, имеющие вершину при центре, называются центральными углами.

Относительно этих углов имеют место следующие теоремы.

Теорема 74. Равным центральным углам в одной и той же окружности соответствуют равные дуги.

Дано. Углы AOB и COD равны (черт. 109).

Требуется доказать, что ◡AB = ◡CD.

Доказательство. Проведем хорды AB и CD и соединим точки A, B, C, D с центром. Два треугольника AOB и COD равны, ибо AO = CO и BO = DO как радиусы, ∠AOB = ∠COD по условию. Следовательно, хорды AB и CD равны.

Против равных хорд лежат равные дуги, следовательно и дуги AB и CD равны: ◡AB = ◡CD (ЧТД).

Теорема 75 (обратная 74). Равным дугам в одной и той же окружности соответствуют равные углы.

Дано. Дуги AB и CD равны (черт. 109).

Требуется доказать, что ∠AOB = ∠COD.

Доказательство. Из того, что дуги AB и CD равны, следует, что и хорды AB и CD тоже равны (теорема 61).

Два треугольника AOB и COD равны, ибо AB = CD как равные хорды, AO = CO и BO = DO как радиусы. Следовательно, ∠AOB = ∠COD (ЧТД).

Теорема 76. Отношение центральных углов равно отношению соответствующих им дуг.

Даны два центральные угла AOB и COD (черт. 110).

Требуется доказать, что

AOB/COD = AB/CD.

Доказательство. Здесь имеют место два случая:

1) Когда дуги AB и CD соизмеримы и 2) когда они несоизмеримы.

1-й случай. Дуги AB и CD соизмеримы.

Пусть дуга AE будет их общей мерой. Положим, что она p раз содержится в дуге AB и q раз в дуге CD. Разделив дугу AB на p, а CD на q равных частей и соединив точки деления дуг с центром O, мы разделим угол AOB на p, а угол COD на q равных углов, из которых каждый равен углу AOE.

Из равенств

AB = pAE, CD = qAE
AOB = pAOE, COD = qAOE

получаем

AOB/COD = p/q, AB/CD = p/q, откуда
AOB/COD = AB/CD (ЧТД).

2-й случай. Дуги AB и CD несоизмеримы.

Отложим дугу AF равную CD и соединим F с O. Углы AOF и COD равны.

Требуется доказать, что

AOB/AOF = AB/AF

Доказательство. A) Положим

AOB/AOF > AB/AF (1).

Для того, чтобы имело место равенство, нужно дробь во второй части неравенства (1) увеличить. Для этого следует ее знаменатель уменьшить.

Положим, мы нашли, что имеет место равенство

AOB/AOF = AB/AG (a)

Разделим дугу AB на равное число таких частей, чтобы каждая часть была менее GF; тогда одна из точек деления i упадет в промежутке между G и F. Дуги AB и Ai соизмеримы, следовательно,

AOB/AOi = AB/Ai (b).

Разделив равенства (b) на (a), находим

AOF/AOi = AG/Ai

равенство несообразное, ибо первая часть его больше, а вторая меньше 1, следовательно, допущение (1) не имеет места.

B) Допустим, что

AOB/AOF < AB/AF (2)

Тогда вторую часть этого неравенства нужно уменьшить для того, чтобы имело место равенство. Для этого нужно знаменатель дроби AB/AF увеличить. Положим, мы нашли такую точку H, чтобы удовлетворялось равенство

AOB/AOF = AB/AH (c)

Разделив дугу AB на такие равные части, чтобы каждая часть была меньше FH, мы найдем, что одна из точек деления J упадет в промежуток между F и H. Дуги AB и AJ будут соизмеримы, следовательно,

AOB/AOJ = AB/AJ (d)

Разделив равенство (d) на (c) найдем

AOF/AOJ = AH/AJ

Это равенство несообразно, ибо первое отношение меньше, а второе больше единицы, следовательно, и допущение (2) тоже не имеет места, откуда видно, что справедливо только равенство AOB/AOF = AB/AF (ЧТД).

Зная, что отношение углов равно отношению дуг, описанных равными радиусами, мы в пропорции (черт. 111)

AOB/COD = AB/CD

можем принять за единицу любую дугу. В этом случае должны принять за единицу и соответствующий ей угол.

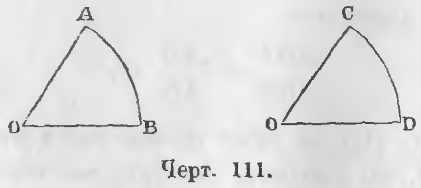
Принимая дугу CD, а следовательно, и угол COD за 1, имеем равенство

AOB/1 = AB/1

или отношение угла к своей единице равно отношению дуги к своей соответствующей единице, откуда

∠AOB = ◡AB.

Это равенство означает, что

числовая величина угла равна числовой величине дуги, или что угол измеряется дугой, описанной из его вершины, как из центра.

Взаимное отношение хорд и их расстояний от центров

Изобразим окружность и ее элементы, согласно теореме:

Заметим, что радиус, обозначенный, как OC, расположен перпендикулярно к хорде AB, как показано на рисунке:

.

Попробуем доказать следующее:

.

Проведем прямую через точки А и В, которая соединит их с центральной точкой О. Заметим, что наклонные OA и OB равны и удалены от перпендикулярной прямой ОС. В результате:

AD = DB.

Предположим, что перпендикулярная прямая CD выходит из середины AB. В таком случае, точка C равноудалена относительно концов перпендикуляра. Из этого следует равенство хорд AC и CB. Таким образом:

.

Получаем, что перпендикуляр OC делит на две равные части дугу AB, что и требовалось доказать.

Начнем доказательство данного утверждения с того, что центральная точка равноудалена от концов хорды. В таком случае, она будет расположена на перпендикуляре, который восстановлен из середины хорды, что и требовалось доказать.

Перенесем данные на рисунок:

Запишем равенство двух хорд AB и CD:

AB = CD

Представим доказательство того, что данные хорды расположены на одинаковом расстоянии от центральной точки:

OE = OF

Если соединить между собой точки A и C, а также центральную точку O, получим пару треугольников AEO и COF, которые равны и являются прямоугольными. Объясним это равенством радиусов:

OA = OC.

Заметим также, что половины одинаковых хорд будут равны друг другу:

AE = CF.

В результате получим доказательство теоремы:

OE = = OF.

Воспользуемся предыдущим рисунком. Запишем, что хорды AB и CDравноудалены от центра:

OE = OF.

Попробуем подтвердить справедливость следующего равенства:

AB = CD.

Рассмотрим пару прямоугольных треугольников AEO и COF. Данные треугольники равны, исходя из равенства гипотенуз и катетов. Согласно условию:

OE = OF

Равенство радиусов:

OA = OC.

В результате получим, что:

AE = CF

Таким образом, теорема доказана:

AB = CD

Заметим, что хорда AB больше по сравнению с хордой AC:

AB > AC

Требуется доказать следующее:

OD < OE

Заметим, что OD расположен перпендикулярно относительно AB. Линия OF является наклонной. В таком случае:

OD < OF

Запишем, что:

OF < OE

В результате теорема доказана:

OD < OE

Уравнения[]

Декартовы координаты

Окружность радиуса r = 1, центр (a, b) = (1.2, -0.5)

Общее уравнение окружности записывается как:

x2+y2+Ax+By+C=,{\displaystyle x^{2}+y^{2}+Ax+By+C=0,\,}

или

(x−x)2+(y−y)2=R2,{\displaystyle \left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}=R^{2},}

где

2x=−A,2y=−B,2R=A2+B2−4C.{\displaystyle 2x_{0}=-A,\;2y_{0}=-B,\;2R={\sqrt {A^{2}+B^{2}-4C}}.}

Точка (x,y){\displaystyle \left(x_{0},y_{0}\right)} — центр окружности, R{\displaystyle R} — её радиус.

Уравнение окружности радиуса R{\displaystyle R} с центром в начале координат:

x2+y2=R2.{\displaystyle x^{2}+y^{2}=R^{2}.\,}

Уравнение окружности, проходящей через три точки (с помощью определителя) (x1,y1),{\displaystyle \left(x_{1},y_{1}\right),} (x2,y2){\displaystyle \left(x_{2},y_{2}\right)} и (x3,y3){\displaystyle \left(x_{3},y_{3}\right):}

|x2+y2xy1x12+y12x1y11x22+y22x2y21x32+y32x3y31|={\displaystyle {\begin{vmatrix}x^{2}+y^{2}&x&y&1\\x_{1}^{2}+y_{1}^{2}&x_{1}&y_{1}&1\\x_{2}^{2}+y_{2}^{2}&x_{2}&y_{2}&1\\x_{3}^{2}+y_{3}^{2}&x_{3}&y_{3}&1\end{vmatrix}}=0.}

Окружность также можно описать с помощью параметрического уравнения:

{x=x+Rcos⁡φy=y+Rsin⁡φ,≤φ<2π.{\displaystyle {\begin{cases}x=x_{0}+R\cos \varphi \\y=y_{0}+R\sin \varphi \end{cases}},\;\;\;0\leq \varphi <2\pi .}

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

y=y±R2−(x−x)2.{\displaystyle y=y_{0}\pm {\sqrt {R^{2}-(x-x_{0})^{2}}}.}

Если центр окружности совпадает с началом координат, функции принимают вид:

y=±R2−x2.{\displaystyle y=\pm {\sqrt {R^{2}-x^{2}}}.}

Полярные координаты

Окружность радиуса R{\displaystyle R} с центром в точке (ρ,ϕ){\displaystyle \left(\rho _{0},\phi _{0}\right)}:

ρ2−2ρρcos⁡(ϕ−ϕ)+ρ2=R2.{\displaystyle \rho ^{2}-2\rho \,\rho _{0}\cos \left(\phi -\phi _{0}\right)+\rho _{0}^{2}=R^{2}.}

Если полярные координаты центра окружности ρ=R,ϕ=α,{\displaystyle \rho _{0}=R,\;\phi _{0}=\alpha ,} то проходящая через начало координат окружность описывается уравнением:

ρ(φ)=2Rcos(φ−α),α−π2≤φ≤α+π2.{\displaystyle \rho (\varphi )=2R\cos \,(\varphi -\alpha ),\;\;\;\alpha -{\frac {\pi }{2}}\leq \varphi \leq \alpha +{\frac {\pi }{2}}.}

Если же центр является началом координат, то уравнение будет иметь вид:

ρ=R.{\displaystyle \rho =R.\,}

Комплексная плоскость

На комплексной плоскости окружность задаётся формулой:

|z−z|=R{\displaystyle \left|z-z_{0}\right|=R\,}

или в параметрическом виде

z=z+Reit,t∈R.{\displaystyle z=z_{0}+Re^{it},\,t\in \mathbb {R} .\,}

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
• Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
• Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
• Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
• Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
• Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
• Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
• Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
• Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
• Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Обруч и окружность

Давайте вспомним один из предметов инвентаря художественной гимнастики  – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца.  Именно с помощью обруча мы приближаемся к термину “окружность”. 

Окружность – это замкнутая кривая, все точки которой равноудалены от центра. 

Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой. 

То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра. 

Чем круг отличается от окружности: объяснение

Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая

Также обратите внимание на отличия между окружностью и кругом:

• Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
• Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
• Сходство между окружностью и кругом: радиус и диаметр;
• У круга и окружности единый центр;
• В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
• У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Элементы круга

Рассмотрим элементы круга. 

Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы. 

Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков. 

Форма кусочков пиццы очень напоминает сектор круга. 

Сектор – это часть круга, которую ограничивают радиусы и дуга. 

При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым. 

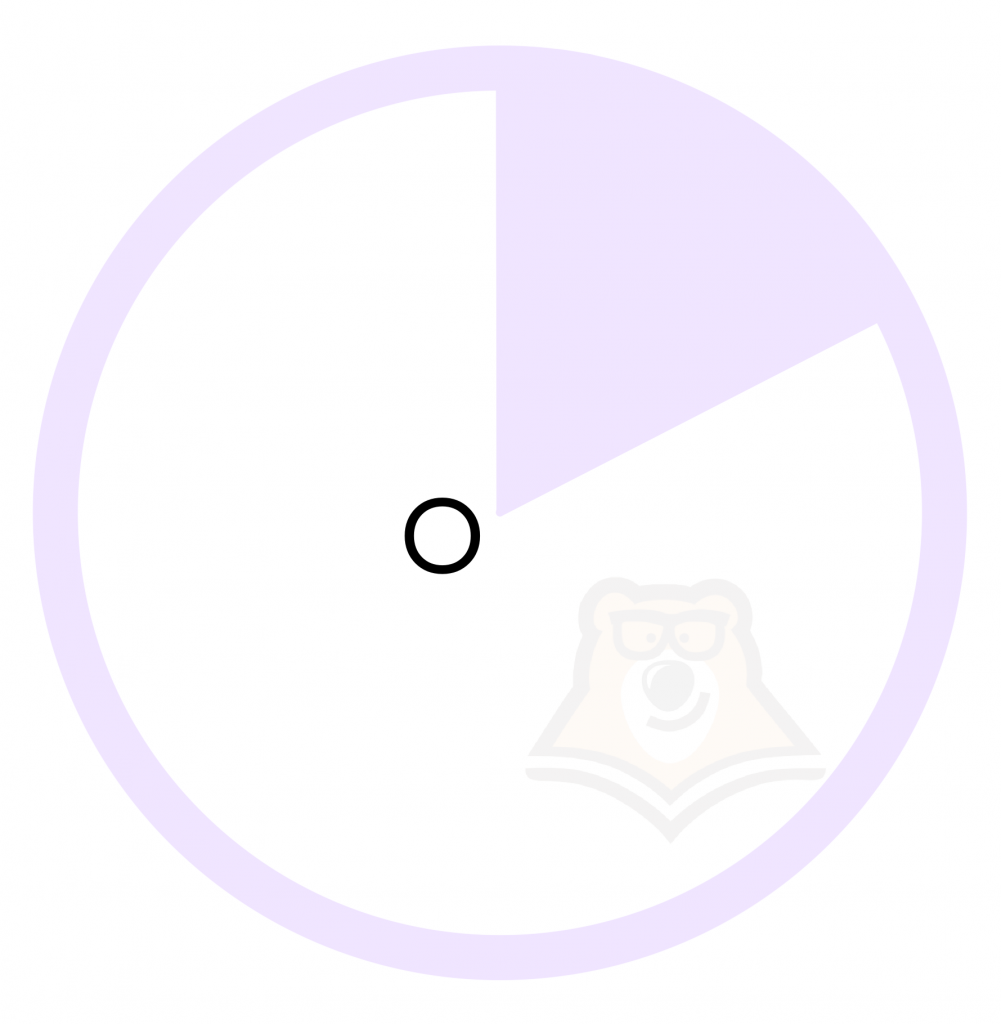
Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга. 

Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину: 

Таким образом, мы отрежем уже не сектор, а сегмент от пиццы. 

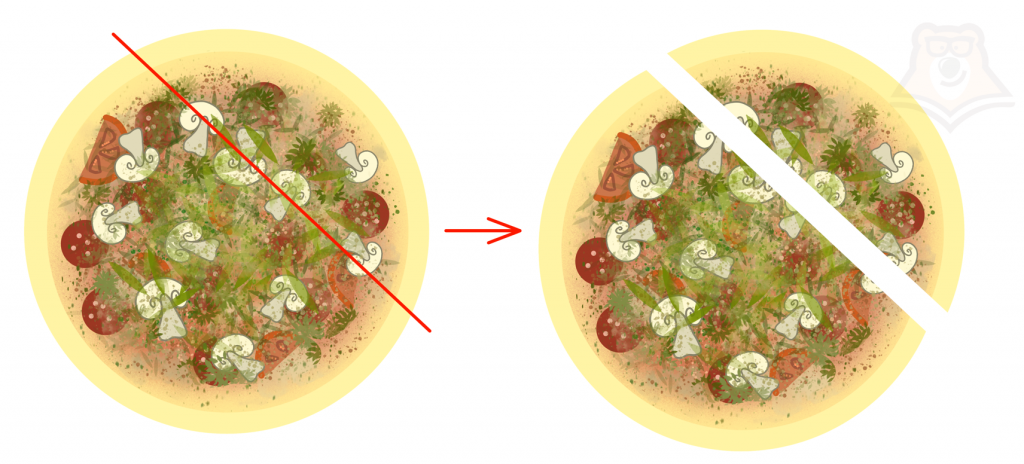
Сегмент – это часть круга, которая ограничена хордой и дугой. 

Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым. 

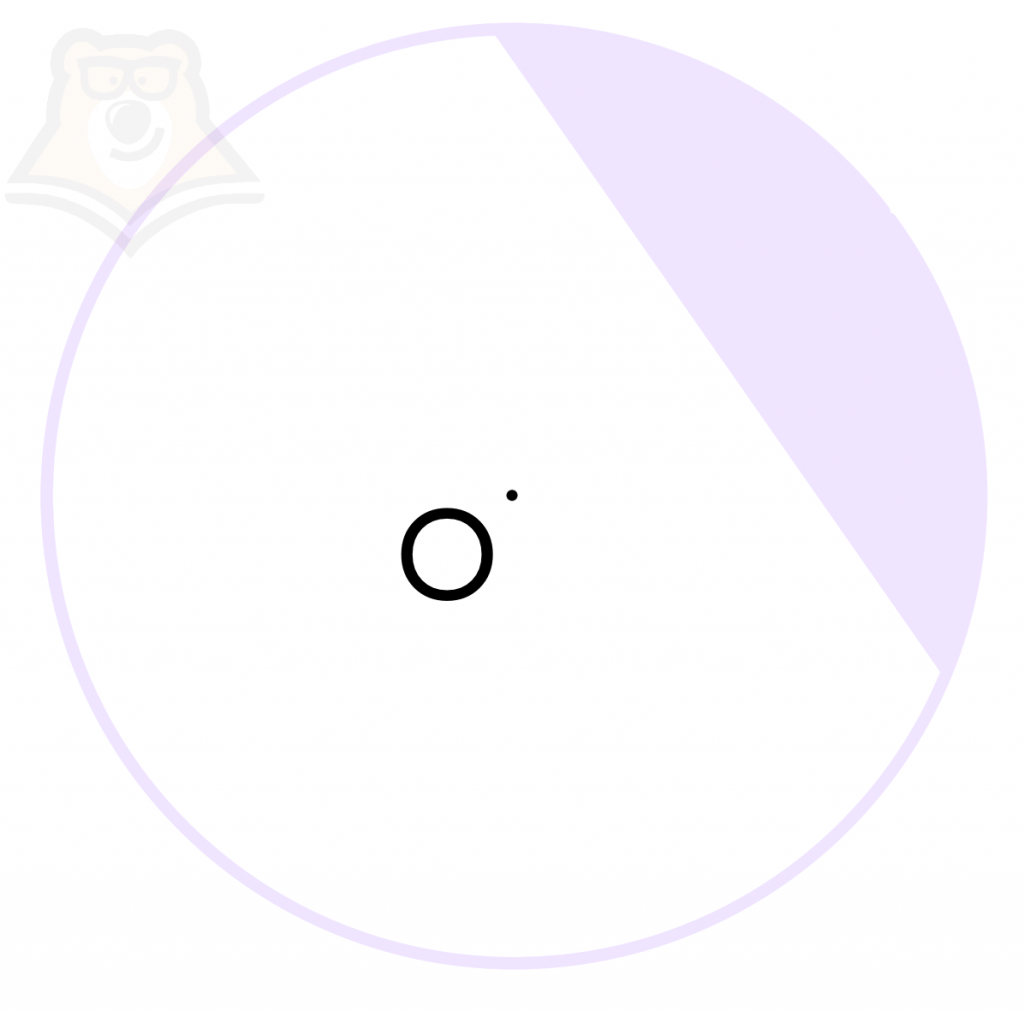
Подведем итог:И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент.

Формулы для окружности и круга

Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их. 

Однако перед этим необходимо ввести еще несколько терминов. 

Длина окружности – это длина кривой, которая образует окружности. 

Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности. 

Длина дуги – это длина части кривой, которая образует окружность. 

Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть. 

В таблице ниже приведены основные формулы, которые могут встретиться при решении задач. 

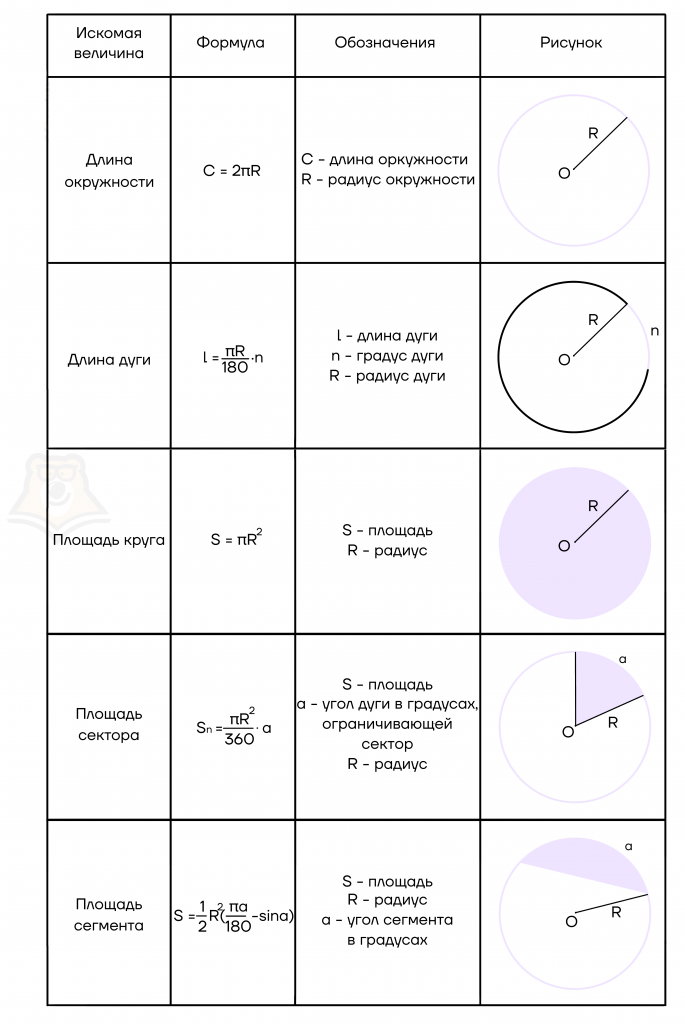
❓Вопросы и ответы

И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.

Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?

Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:

• Площадь круга
• Длина окружности
• Диаметр
• Радиус

Какие есть ещё калькуляторы для круга у вас на сайте?

У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.

Почему Пи равняется 3,1415926…, а не является «ровным» числом?

Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.

Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?

Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.

4 теоремы про окружность в ЕГЭ и ОГЭ

Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.

Теорема № 1: теория и задания из ЕГЭ и ОГЭ

Первая теорема про хорду и касательную звучит так: 

Угол между касательной и хордой равен половине дуге, которую стягивает хорда.

Подробнее с выведением вы можете ознакомиться на рисунке:

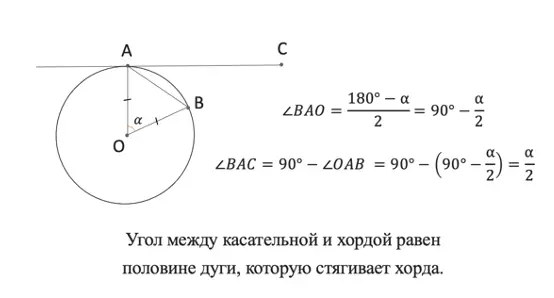Вот так выводится теорема про хорду и касательную

Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:. Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную

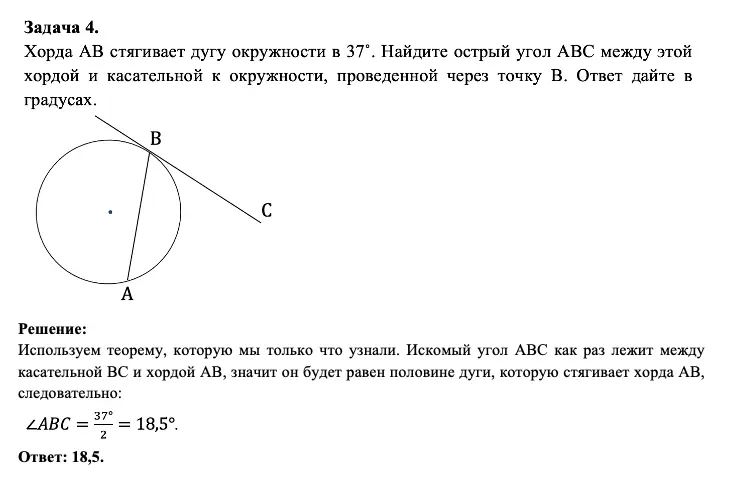Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную

Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!

Теорема № 2: теория и задания из ЕГЭ и ОГЭ

А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:

Квадрат касательной равен произведению секущей на её внешнюю часть. Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.

Наглядно познакомиться с теоремой можно на рисунке ниже:

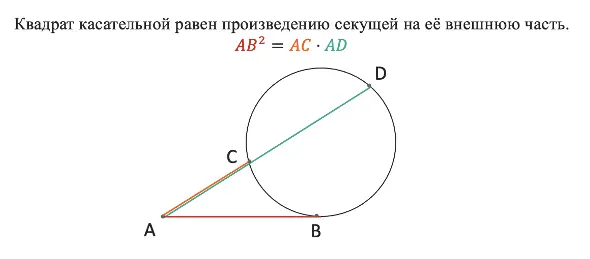Теорема: квадрат касательной равен произведению секущей на её внешнюю часть

И конечно же давайте отработаем на практике!

Пример задания на теорему № 2

Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!

Решение:

Вот так просто решается это задание!

Теорема № 3: теория и задания из ЕГЭ и ОГЭ

Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).

Эта теорема интересна тем, что работает в обе стороны:

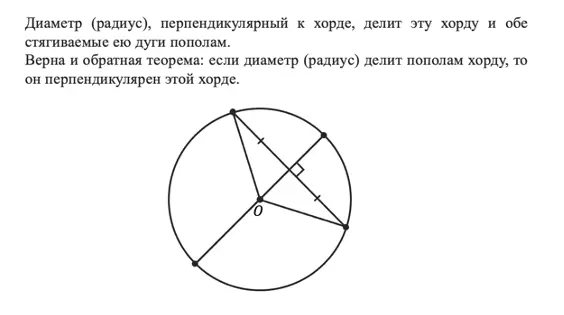Вот так хорду можно связать с диаметром (радиусом)

Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:

Задание на нашу теорему и его решение

Теорема № 4: пересекающиеся хорды

Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд: 

Произведения отрезков пересекающихся хорд равны.

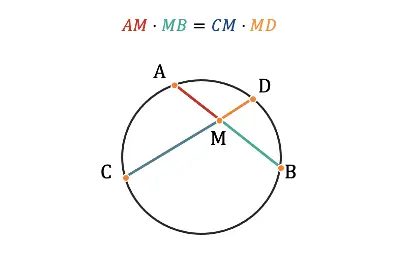Свойство пересекающихся хорд на рисунке

Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.

А теперь отработаем его на практике:

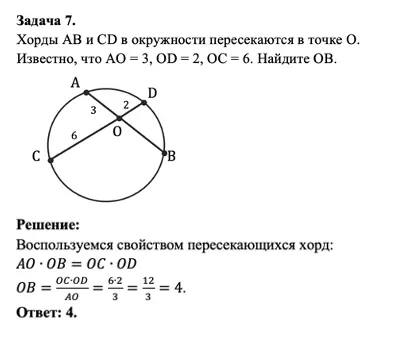Задание на свойство пересекающихся хорд и его решение

Вписанные и описанные окружности

Окружность и треугольник

• центр вписанной окружности — точка пересечения
  ,
  ее радиус r вычисляется по формуле:

r = ,

где S — площадь треугольника, а —
полупериметр;

центр описанной окружности — точка пересечения
,
ее радиус Rвычисляется по формуле:

R =
,

R = ;

здесь a, b, c — стороны треугольника,
— угол, лежащий против стороны a, S — площадь треугольника;

центр описанной около окружности лежит на середине ;

центр описанной и вписанной окружностей треугольника совпадают только
в том случае, когда этот треугольник — .

Окружность и четырехугольники

• около
  можно описать окружность тогда и только тогда, когда сумма его внутренних
  противоположных углов равна 180°:

 +
 =  +
 = 180°;

в можно вписать
окружность тогда и только тогда, когда у него равны суммы противоположных
сторон:

a
+ c = b + d;

• около можно
  описать окружность тогда и только тогда, когда он является ;
• около
  можно описать окружность тогда и только тогда, когда эта
  — ; центр
  окружности лежит на пересечении оси симметрии
  с
  к боковой стороне;
• в можно вписать
  окружность тогда и только тогда, когда он является .

Длина окружности

Рассмотрим – угольникnправильный     B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центра O окружности перпендикуляры на все стороны многоугольника (рис. 2).

Рис.2

Поскольку – угольникаnплощадь   B1B2…Bn   равна

то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R:

C = 2πR.

Следствие. Длина окружности радиуса 1 равна   2π.

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

l=πd, где

π— число пи — математическая константа, равная 3,14

d — диаметр окружности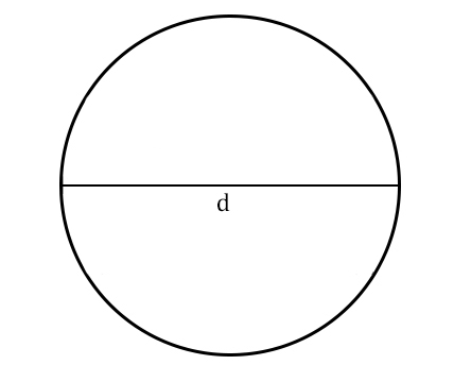

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

l=2πr , где

π — число пи, равное 3,14

r — радиус окружности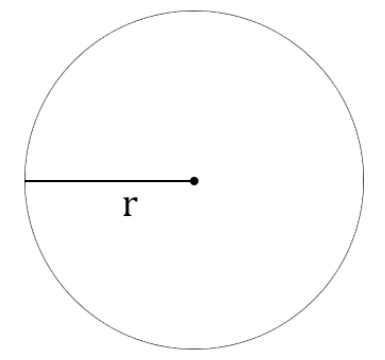

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

где:

• π — число пи, равное 3,14
• S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник: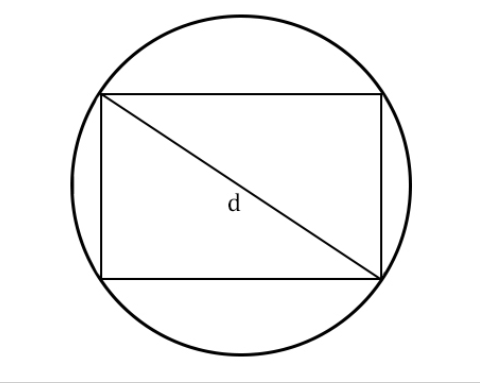

l=πd, где

• π — число пи, равное 3,14
• d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата: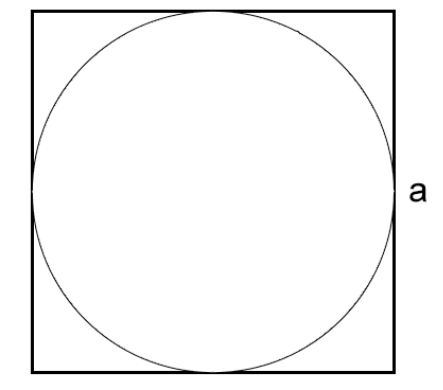

l=πa, где

• π — математическая константа, равная 3,14
• a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

где:

• π — математическая константа, она всегда равна 3,14
• a — первая сторона треугольника
• b — вторая сторона треугольника
• c — третья сторона треугольника
• S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

где:

• π — математическая константа, равная 3,14
• S — площадь треугольника
• p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:

где:

• π — математическая константа, равная 3,14
• a — сторона многоугольника
• N — количество сторон многоугольника