Прямоугольник, свойства, признаки и формулы

Применение прямоугольников в повседневной жизни

Прямоугольники являются одним из наиболее распространенных геометрических фигур в нашей повседневной жизни. Мы можем встретить их в самых разных местах и ситуациях.

• В строительстве и архитектуре прямоугольники используются для построения стен, полов, оконных и дверных проемов.
• В мебельном производстве прямоугольники также являются основной формой многих предметов мебели, таких как столы, шкафы, кровати и прочее.
• В производстве электроники и бытовой техники прямоугольники встречаются как корпуса различных устройств и приборов.
• В промышленности прямоугольники используются для изготовления упаковок, ящиков и контейнеров различных видов.
• В сфере дизайна и графики прямоугольники широко используются как основные элементы оформления и композиции.

Таким образом, прямоугольники стали неотъемлемой частью нашего быта и повседневной жизни, позволяя нам производить и использовать различные предметы и конструкции.

Формулы

S = а ⋅ б

 Периметр прямоугольника (P):

Р = а + а + б + б = 2а + 2б

Формулы определения длин сторон прямоугольника

 Формула стороны прямоугольника (длина и ширина прямоугольника) через диагональ и другую сторону:

а = √d2 — b2

б = √d2 — а2

 Формула стороны прямоугольника (длина и ширина прямоугольника) через площадь и другую сторону:

а =	С
б

б =	С
один

 Формула стороны прямоугольника (длина и ширина прямоугольника) через периметр и другую сторону:

а =	П-2б
2

б =	Р-2а
2

 Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол α:

а = dsinα

b = d cosα

 Формула стороны прямоугольника (длина и ширина прямоугольника) через диаметр и угол β:

а = d грех	β
2

б = dcos	β
2

Формулы определения длины диагонали прямоугольника

 Формула диагонали прямоугольника через две стороны прямоугольника (по теореме Пифагора):

d = √a2 + b2

 Формула диагонали прямоугольника через площадь и любую сторону:

д =	√С2 + а4	=	√S2 + b4
один	б

 Формула диагонали прямоугольника через периметр и любую сторону:

д =	√P2 — 4Па + 8а2	=	√P2 — 4Pb + 8b2
2	2

 Формула диагонали прямоугольника через радиус описанной окружности:

д=2R

 Формула диагонали прямоугольника через диаметр описанной окружности:

д = сделать

 Формула диагонали прямоугольника в виде синуса угла, примыкающего к диагонали, и длины стороны, противолежащей этому углу:

д =	один
син

 Формула диагонали прямоугольника в виде косинуса угла, следующего за диагональю, и длины стороны, следующего за этим углом:

д =	б
коса

 Формула диагонали прямоугольника через синус острого угла между диагоналями и площадь прямоугольника

d = √2S : sinβ

Формулы определения длины периметру прямоугольника

 Формула периметра прямоугольника через две стороны прямоугольника:

Р = 2а + 2б

Р = 2 (а + б)

 Формула периметра прямоугольника через площадь и любую сторону:

П =	2С + 2а2	=	2с + 2б2
один	б

 Формула периметра прямоугольника через диагональ и любую сторону:

P = 2(a + √d2 — a2) = 2(b + √d2 — b2)

 Формула периметра прямоугольника через радиус описанной окружности и любую сторону:

P = 2(a + √4R2 — a2) = 2(b + √4R2 — b2)

 Формула периметра прямоугольника через диаметр описанной окружности и любую сторону:

P = 2(a + √Do2 — a2) = 2(b + √Do2 — b2)

Формулы определения радиуса окружности описанной вокруг прямоугольника

 Формула радиуса окружности, описанной вокруг прямоугольника через две стороны:

Р =	√а2 + б2
2

 Формула радиуса окружности, описанной вокруг прямоугольника через периметр квадрата и любую сторону:

Р =	√P2 — 4Па + 8а2	=	√P2 — 4Pb + 8b2
4	4

 Формула радиуса окружности, описанной вокруг прямоугольника, через площадь квадрата:

Р =	√С2 + а4	=	√S2 + b4
2а	2б

 Формула радиуса окружности, описанной вокруг прямоугольника через диагональ квадрата:

Р =	д
2

 Формула радиуса окружности, описанной вокруг прямоугольника, через диаметр описанной окружности:

Р =	Делать
2

 Формула радиуса окружности, описанной вокруг прямоугольника, в виде синуса угла, прилежащего к диагонали, и длины стороны, противолежащей этому углу:

Р =	один
2 синα

 Формула радиуса окружности, описанной вокруг прямоугольника, в виде косинуса угла, следующего за диагональю, и длины стороны, следующего за этим углом:

Р =	б
2cosα

 Формула радиуса окружности, описанной вокруг прямоугольника, в виде синуса острого угла между диагоналями и площади прямоугольника:

Р =	√2S : sinβ
2

Формулы определения угла между стороной и диагональю

 Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:

sinα =	один
д

cosα =	б
д

 Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:

α =	β
2

Формулы определения угла между диагоналями прямоугольника

 Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:

β = 2α

 Формула определения угла между диагоналями прямоугольника через площадь и диагональю:

грех β =	2С
d2

Примеры вопросов и задач

Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.

Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?

Решение Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.

Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?

Решение Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.

Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.

Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.

Вопрос 2. У прямоугольника все стороны равны или нет?

Решение Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.

Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.

Решение По формулам для квадрата проведём следующие расчёты:

• Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17, d = a √2 =1 7√2.
• Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
• Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.

Свойства прямоугольника

К свойствам прямоугольника относятся следующие утверждения:

1. Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
   1. У прямоугольника равны противоположные стороны.

Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:

Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:

К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.

Прямоугольник отличается от квадрата, этому учат в школе в младших классах. Квадрат — это одинаковая длина соединяющих углов, если я правильно выражаюсь, а прямоугольник формы может быть: телефон, звуковые колонки, паспорт и прочее.

Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.

Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.

Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.

Какой четырёхугольник называется прямоугольником

В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.

Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.

• Признаки и свойства прямоугольника
• Формулы для вычисления длины сторон
• Периметр и площадь
• Диагонали прямоугольника
• Определение и свойства квадрата
• Примеры вопросов и задач

Признаки и свойства прямоугольника

Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:

• фигура является четырёхугольником, три угла которого равны 90°,
• представленный четырёхугольник — это параллелограмм с равными диагоналями,
• параллелограмм, который имеет по крайней мере один прямой угол.

Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.

Формулы для вычисления длины сторон

В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).

Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:

• С использованием диагонали и известной стороны: a = √(d ² b ²), b = √(d ² a ²).
• По площади фигуры и одной из её сторон: a = S / b, b = S / a.
• При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
• Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
• Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.

Признаки

Перед нами параллелограмм. Как доказать, что он является прямоугольником? Воспользоваться одним из признаков:

Параллелограмм является прямоугольником, если один из углов – прямой.

В параллелограмме противоположные углы равны. Значит, если один из углов – прямой, то противоположный ему угол так же прямой, а два оставшихся равны между собой. Сумма всех углов четырехугольника 360 градусов.

Два угла прямые, значит остается 360-90*2=180. Эта сумма двух равных углов, значит, каждый из оставшихся углов прямой: 180/2=90. Если все углы параллелограмма прямые, то это прямоугольник.

Этот признак работает только для параллелограммов. В случае с четырехугольниками прямой угол может быть и у прямоугольной трапеции.

Рис. 1. Прямоугольная трапеция.

Если вокруг параллелограмма можно описать окружность, то это прямоугольник.

Для того, чтобы вокруг четырехугольника описать окружность, необходимо, чтобы противоположные углы в сумме давали 180 градусов. Противоположные углы в параллелограмме равны, значит 180/2=90 градусов составляет каждый угол. Значит это прямоугольник.

Рис. 2. Прямоугольник, вписанный в окружность.

• Если в четырехугольнике все углы равны, то он является прямоугольником. Для этого признака необязательно убеждаться, что перед вами параллелограмм. В любом четырехугольнике сумма углов равна 360. Если все углы равны, то 360/4=90 градусов составляет каждый из углов. Вот и получается, что в любом случае это прямоугольник.
• Если в параллелограмме диагонали равны, то это прямоугольник. Для доказательства нужно провести две диагонали и рассмотреть получившиеся треугольники. Треугольники АВD и АСD равны по трем сторонам. Основание у них общее, диагонали равны, а третья сторона это две противоположные стороны параллелограмма, которые так же равны между собой. Равны треугольники, значит, равны и их части: смежные углы параллелограмма равны, значит, все углы параллелограмма равны между собой. Перед нами прямоугольник.

Рис. 3. Рисунок к доказательству.

• Если в четырехугольнике три угла прямые, то он является прямоугольником. Если посчитать, то четвертый угол в таком случае будет равен: 360-90*3=90, то есть и четвертый угол будет прямым.
• Если квадрат диагонали равен сумме квадратов двух смежных сторон. В этом случае диагональ является гипотенузой, а стороны катетами прямоугольного треугольника по теореме, обратной теореме Пифагора (это один из признаков прямоугольного треугольника).

Это существенные признаки прямоугольников. Существуют так же дополнительные, которые сводятся к уже перечисленным. И главное, помните, что в математике важны определения. Признаки прямоугольного прямоугольника – неправильная формулировка. Прямоугольник всегда был, есть и будет прямоугольным.

Что мы узнали?

Мы разобрались как можно доказать, что параллелограмм или четырехугольник является параллелограммом, вспомнили некоторые определения и ознакомились с ведущим методом определения прямоугольника – по углам.

1. /5

   Вопрос 1 из 5

Прямоугольник — это одна из основ геометрии

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.

Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.

Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.

Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».

Примеры решения задач

Пример

Упражнение. В прямоугольнике $ABCD$ одна сторона на 2 см длиннее другой. Найдите стороны прямоугольника, периметр которого равен 20 см.

Решение. Сделаем чертеж (рис. 2)

Пусть наименьшая сторона прямоугольника равна $x$ см, тогда большая сторона равна $(x+2)$ см. Поскольку периметр равен $P_{ABCD}=2(AB+AD)=20$, мы получаем следующее уравнение

$2(х+(х+2))=20$

$х+х+2=20 : 2$

$quad 2 x=10-2$

$quad 2 x=8$

$х=4$

Таким образом, $AB=CD=4$ см, $AD=BC=6$ см.

Отвечать. $AB=CD=4$ см, $AD=BC=6$ см.

Упражнение. Окружность радиуса $R$ описана вокруг прямоугольника $ABCD$ со сторонами 12 дм и 5 дм. Найдите $R$.

Решение. Сделаем чертеж (рис. 3.)

Радиус описанной окружности равен половине диагонали. Найдем диагональ. Рассмотрим $Delta ABD$, он прямоугольный ($angle A=90^{circ}$). По теореме Пифагора:

$$BD=sqrt{AB^{2}+AD^{2}}$

подставляя значения сторон, получаем

$BD=sqrt{12^{2}+5^{2}}$

$BD=sqrt{144+25}=sqrt{169}$

$BD=13$ (дм)

Тогда $R=frac{BD}{2} Rightarrow R=frac{13}{2} Rightarrow R=6.5$ (дм)

Отвечать. $R=6,5$ дм

Периметр и площадь

Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:

Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:

К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Три способа найти длину прямоугольника

Если вы разделите фигуру на две части диагональю, то заметите, что прямоугольник делит ее на два прямоугольных треугольника. Из этого деления следуют все формулы длины прямоугольника.

Через теорему Пифагора

Если известна длина диагонали (обозначим ее буквой d) и длина прямоугольника (примем значение за букву а). Тогда квадратный корень из разницы между квадратами диагонали и длины будет равен ширине прямоугольника.

Чтобы было понятнее, запишем решение в виде нескольких формул.

По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Гипотенуза — сторона, лежащая против прямого угла, две другие стороны называются катетами. В нашем случае гипотенуза — это диагональ.

Итак: d2=a2+b2 . Из этого выражения выражаем квадрат ширины (значение «b»): b2=d2-a2

Чтобы определить значение b, извлеките квадратный корень из обеих частей полученного выражения: b=(d2-a2)(-1)

При необходимости вы можете поменять местами a и b, и вы получите формулу длины.

Через площадь

Рассмотрим еще один способ нахождения длины прямоугольника — через площадь. Площадь прямоугольника равна произведению длины на ширину. То есть использовать уже известное обозначение S=a*b. Выразим значение ширины из этой формулы: b=S/b.

Как и в первом методе, вы можете поменять местами a и b, чтобы получить формулу длины: a=S/b.

Тригонометрическая функция

Один из самых быстрых, но и несколько сложных способов нахождения длины — использование тригонометрической функции.

Если это прямоугольный треугольник, существуют соотношения, известные как синус и косинус соответственно.

Выберем угол между длиной и диагональю. Обозначим его через α. Тогда sin α равен отношению между катетом, противолежащим углу α, и гипотенузой: Sin α = a/c

Рис. 2. Угол альфа на половине прямоугольника

Значение синуса любого угла можно найти в таблицах Брадиса или воспользовавшись калькулятором. Для удобства можно использовать онлайн-версию, которая автоматически находит значение коэффициента.

Но в формуле нет значения b, которое соответствует длине, а значит будем использовать основное тригонометрическое тождество. Косинус – это отношение катета, следующего за углом, к гипотенузе: cos a=b/c

Таким образом, вы можете найти длину, умножив косинус на гипотенузу: b=cos α*c

Признаки прямоугольника

У прямоугольника всего три основных признака:

По углу. Если один из углов параллелограмма равен 90 градусам, то параллелограмм является прямоугольником.
Если три угла четырехугольника равны 90 градусам, то такой четырехугольник является прямоугольником

Обратите внимание, что в этом случае нет необходимости доказывать, что перед нами параллелограмм. Достаточно знать значения углов четырехугольника.
По диагоналям: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.

Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве. В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других

Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки

В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.

Что мы узнали?

Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника

Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма

1. /10

   Вопрос 1 из 10

Общая информация

В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.

Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.

Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.

Главные признаки прямоугольника

Прямые углы – это главный признак прямоугольника. Прямой угол имеет точно 90 градусов и делим на два одинаковых прямых угла.

Конечные точки – каждая вершина прямоугольника связана с другими двумя точками, чтобы образовать одинаковый угол. Две противоположные точки должны иметь одинаковую или параллельную линию.

Противоположные стороны – это группа линий, которые соединяют между собой противоположные вершины фигуры. Отличительной особенностью противоположных сторон является их одинаковая длина и жесткая параллельность.

Равные противоположные углы – в прямоугольнике существует две группы вершин, которые образуют равные углы друг с другом. Углы находятся ближе к соседней точке, и они расположены по обе стороны от главной диагонали.

Диагонали – это линии, которые соединяют противоположные вершины фигуры, начиная от одного угла к другому. Диагонали прямоугольника равны друг другу в длине и разделяют данный четырехугольник на два треугольника.

Периметр и площадь – это основные характеристики прямоугольника, важные для расчета. Периметр равен сумме всех четырех сторон, а площадь вычисляется как произведение длины и ширины.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

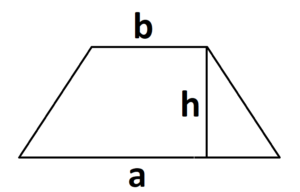
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Круг

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

1. S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
2. S = π × d2 : 4, где d — это диаметр.
3. S = L2​ : (4 × π), где L — это длина окружности.

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.