Влияние температуры на направление реакции[править]
По формуле зависимости энергии Гиббса от энтропии, энтальпии и температуры очевидно, что влияние температуры определяется знаком и величиной энтропии. Для реакции, протекающей с увеличением энтропии, повышение температуры уменьшает энергию Гиббса (то есть благоприятствует протеканию процесса). Для реакции, протекающей с уменьшением энтропии, повышение температуры препятствует протеканию процесса. Это приводит к тому, что некоторые вещества при определенных температурах образуют одни соединения, а при других температурах — другие.
Процессы, протекающие с уменьшением энтальпии (ΔН < 0) и увеличением энтропии (ΔS > 0), практически необратимы. Вне зависимости от температуры, энергия Гиббса будет здесь отрицательной.
4.6. Энергия Гиббса window.top.document.title = «4.6. Энергия Гиббса»;
Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным T ΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж):
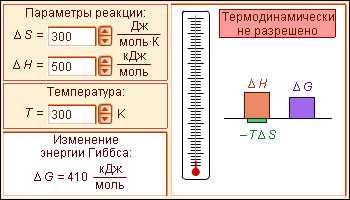 |
|
Модель 4.10. Энергия Гиббса |
При ΔG < 0 реакция термодинамически разрешена и система стремится к достижению условия ΔG = 0, при котором наступает равновесное состояние обратимого процесса; ΔG > 0 указывает на то, что процесс термодинамически запрещен (рис. 4.4).
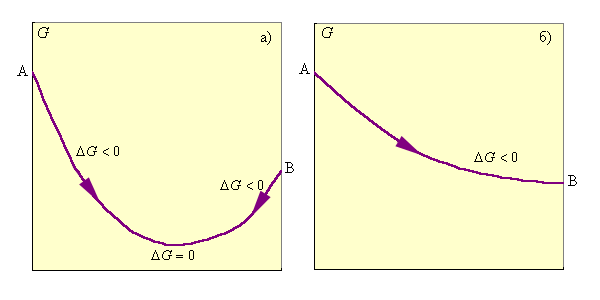 |
| Рисунок 4.4Изменение энергии Гиббса: а – обратимый процесс; б – необратимый процесс |
Записав уравнение (4.2) в виде ΔH = ΔG + T ΔS, получим, что энтальпия реакции включает свободную энергию Гиббса и «несвободную» энергию ΔS · T. Энергия Гиббса, представляющая собой убыль изобарного (P = const) потенциала, равна максимальной полезной работе. Уменьшаясь с течением химического процесса, ΔG достигает минимума в момент равновесия (ΔG = 0). Второе слагаемое ΔS · T (энтропийный фактор) представляет ту часть энергии системы, которая при данной температуре не может быть превращена в работу. Эта связанная энергия способна лишь рассеиваться в окружающую среду в виде тепла (рост хаотичности системы).
Итак, в химических процессах одновременно изменяются энергетический запас системы (энтальпийный фактор) и степень ее беспорядка (энтропийный фактор, не совершающая работу энергия).
Анализ уравнения (4.2) позволяет установить, какой из факторов, составляющих энергию Гиббса, ответственен за направление протекания химической реакции, энтальпийный (ΔH) или энтропийный (ΔS · T).
-
Если ΔH < 0 и ΔS > 0, то всегда ΔG < 0 и реакция возможна при любой температуре.
-
Если ΔH > 0 и ΔS < 0, то всегда ΔG > 0, и реакция с поглощением теплоты и уменьшением энтропии невозможна ни при каких условиях.
-
В остальных случаях (ΔH < 0, ΔS < 0 и ΔH > 0, ΔS > 0) знак ΔG зависит от соотношения ΔH и TΔS. Реакция возможна, если она сопровождается уменьшением изобарного потенциала; при комнатной температуре, когда значение T невелико, значение TΔS также невелико, и обычно изменение энтальпии больше TΔS. Поэтому большинство реакций, протекающих при комнатной температуре, экзотермичны. Чем выше температура, тем больше TΔS, и даже эндотермические реакции становятся осуществляемыми.
Проиллюстрируем эти четыре случая соответствующими реакциями:
| 1. | ΔH < 0ΔS > 0ΔG < 0 | C2H5–O–C2H5 + 6O2 = 4CO2 + 5H2O(реакция возможна при любой температуре) |
| 2. | ΔH > 0ΔS < 0ΔG > 0 | реакция невозможна |
| 3. | ΔH < 0ΔS < 0ΔG > 0, ΔG < 0 | N2 + 3H2 = 2NH3 (возможна при низкой температуре) |
| 4. | ΔH > 0ΔS > 0ΔG > 0, ΔG < 0 | N2O4(г) = 2NO2(г) (возможна при высокой температуре). |
Для оценки знака ΔG реакции важно знать величины ΔH и ΔS наиболее типичных процессов. ΔH образования сложных веществ и ΔH реакции лежат в пределах 80–800 кДж∙
Энтальпия реакции сгорания всегда отрицательна и составляет тысячи кДж∙. Энтальпии фазовых переходов обычно меньше энтальпий образования и химической реакции Δ – десятки кДж∙, Δ и Δ равны 5–25 кДж∙.
Зависимость ΔH от температуры выражается соотношением ΔHT = ΔH° + ΔCp · ΔT, где ΔCp – изменение теплоемкости системы. Если в интервале температур 298 К – T реагенты не претерпевают фазовых превращений, то ΔCp = 0, и для расчетов можно пользоваться значениями ΔH°.
Энтропия индивидуальных веществ всегда больше нуля и составляет от десятков до сотен Дж∙моль–1K–1 (табл. 4.1). Знак ΔG определяет направление реального процесса. Однако для оценки осуществимости процесса обычно пользуются значениями стандартной энергии Гиббса ΔG°. Величина ΔG° не может использоваться в качестве критерия вероятности в эндотермических процессах со значительным возрастанием энтропии (фазовые переходы, реакции термического разложнения с образованием газообразных веществ и др.). Такие процессы могут быть осуществлены за счет энтропийного фактора при условии
 |
|
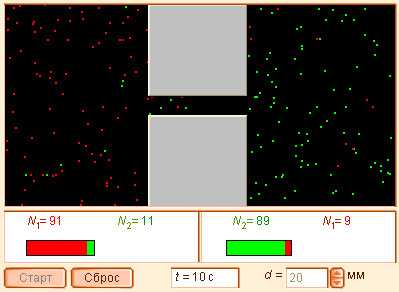
Модель 4.11. Диффузия газов |
Примеры решения задач
Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:
Объяснить знак и величину ΔS о .
Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | NH3(г) | O2(г) | NО(г) | H2O(ж) |
| S о 298,
Дж/(моль·К) |
192,66 | 205,04 | 210,64 | 69,95 |
В данной реакции ΔV o х.р.,298
Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH4NO3(к). Отличается ли стандартная энтропия образования NH4NO3(к) от стандартной энтропии этого соединения?
Решение. Стандартной энтропии образования NH4NO3 отвечает изменение энтропии в процессе:
Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2(г) | H2(г) | O2(г) | NH4NO3(к) |
| S о 298,
Дж/(моль·К) |
191,50 | 130,52 | 205,04 | 151,04 |
Стандартная энтропия образования NH4NO3(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S о 298(NH4NO3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S о 298 всегда больше нуля, в то время как величины ΔS 0 f,298, как правило, знакопеременны.
Задача 3. Изменение энергии Гиббса реакции:
равно δG о 298= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.
Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS о о 298 реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS о
Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:
Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | С4Н10(г) | С2Н4(г) | Н2(г) |
| ΔG о f,298× , кДж/моль | — 17,19 | 68,14 | |
| S о 298, Дж/(моль·К) | 310,12 | 219,45 | 130,52 |
ΔG о х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.
Поскольку ΔS о х.р.,298 > 0, то при температуре Т>ΔН о /ΔS о величина ΔG о х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.
Задача 5. Пользуясь справочными данными по ΔG о f,298 и S о 298, определите ΔH о 298 реакции:
Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:
| Вещество | N2O(г) | H2(г) | N2H4(г) | H2O(ж) |
| ΔG о f,298, кДж/моль | 104,12 | 159,10 | -237,23 | |
| S о 298, Дж/(моль·К) | 219,83 | 130,52 | 238,50 | 69,95 |
ΔG о 298 = ΔН о 298 – ТΔS о 298. Подставляя в это уравнение величины ΔН о 298 и ТΔS о 298, получаем:
ΔН о 298 = –182,25× 10 3 + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.
Следует подчеркнуть, что поскольку ΔS о 298 выражена в Дж/(моль× К), то при проведении расчетов ΔG 0 298 необходимо также выразить в Дж или величину ΔS 0 298 представить в кДж/(мольK).
Определение[]
Энергией Гиббса (или потенциалом Гиббса, или просто термодинамическим потенциалом в узком смысле) называют термодинамический потенциал следующего вида:
G=U+PV−TS{\displaystyle \,\!G=U+PV-TS},
где U — внутренняя энергия, P — давление, V — объем, T — абсолютная температура, S — энтропия.
Энергию Гиббса можно понимать как полную химическую энергию системы (кристалла, жидкости и т.д.)
Дифференциал энергии Гиббса для системы с постоянным числом частиц:
dG=−SdT+VdP{\displaystyle \,\!dG=-SdT+VdP}.
Для системы с переменным числом частиц этот дифференциал записывается так:
dG=−SdT+VdP+μdN{\displaystyle \,\!dG=-SdT+VdP+\mu dN}.
Здесь μ{\displaystyle \mu } — химический потенциал, который можно определить как энергию, которую необходимо затратить, чтобы добавить в систему ещё одну частицу.
Можно показать, что химический потенциал есть отношение энергии Гиббса к числу частиц в системе:
μ=GN{\displaystyle \,\!\mu ={\frac {G}{N}}}.
Химический потенциал применяется при анализе систем с переменным числом частиц, а также при изучении фазовых переходов.
Можно показать, что минимум потенциала Гиббса соответствует устойчивому равновесию термодинамической системы с фиксированными температурой, давлением и числом частиц.
Энтальпийный, энтропийный фактор и направление процесса
Проанализируем уравнение ΔG о Т = ΔН о Т — ΔТS о Т. При низких температурах ТΔS о Т мало. Поэтому знак ΔG о Т определяется в основном значением ΔН о Т (энтальпийный фактор). При высоких температурах ТΔS о Т – большая величина, знак Δ G о Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН о Т) и энтропийного (ТΔS о Т) факторов существует четыре варианта процессов.
-
-
- Если ΔН о Т о Т > 0, то ΔG о Т
- Если ΔН о Т > 0, ΔS о Т о Т > 0 всегда (процесс не протекает ни при какой температуре).
- Если ΔН о Т о Т о Т о /ΔS о (процесс идет при низкой температуре за счет энтальпийного фактора).
- Если ΔН о Т > 0, ΔS о Т > 0, то ΔG о Т ΔН о / ΔS о (процесс идет при высокой температуре за счет энтропийного фактора).
-
Абсолютная энтропия веществ и изменение энтропии в процессах
При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.
Изменение энтропии в процессе выражается уравнением:
где S(прод.) и S(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.
На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δnг. Так, для реакции
(Δnг = 1) ΔV > 0, значит, ΔS > 0.































