История возникновения геометрии: кто и зачем создал, когда открыли науку

Пифагор Пифагор Самосский. (ок. 580 – ок. 500 г. до н.э.)

(Пифагор VI век до н.э., основал свою школу).

Пифагор известен как великий ученый – философ, математик, выдающийся оратор и тонкий психолог.

Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя. Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго до него. В вавилонских текстах она встречается за 1200 лет до Пифагора. По-видимому, он первым нашёл её доказательство. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим свидетельствам – даже сто быков. Это, однако, противоречит сведениям о моральных и религиозных воззрениях Пифагора. В литературных источниках можно прочитать, что он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». В связи с этим более правдоподобной можно считать следующую запись: «… когда он открыл, что в прямоугольном треугольнике гипотенуза имеет соответствие с катетами, он принес в жертву быка, сделанного из пшеничного теста».

Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

теорема о сумме внутренних углов треугольника;

построение правильных многоугольников и деление плоскости на некоторые из них;

геометрические способы решения квадратных уравнений;

деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

доказательство того, что не является рациональным числом;

создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое. (Слайд 16).

Изучение до нашей эры

Развитие геометрии связано с трудами многих исследователей. Весомый вклад в эти работы внесли Евклид и Архимед.

Труды Евклида

Благодаря Евклиду Александрийскому была создана «современная геометрия». Этот ученый ввел понятие математической строгости и аксиоматического метода, который применяется по сей день. Его книга «Начало» была написана примерно 300 лет до нашей эры. Она представляет собой наиболее влиятельный учебник всех времен и народов. Этот труд был известен всем образованным людям в западных странах вплоть до середины двадцатого века.

Благодаря Евклиду появилось 23 определения, 5 постулатов и 5 аксиом. Элементы теории Евклида легли в основу современной геометрии, которая по сей день преподается в учебных заведениях.

Труды Архимеда

Архимед считается автором формулы, которая помогает определять площадь треугольника через три его стороны. Ее ошибочно называют формулой Герона. Также Архимед создал теорию полуправильных выпуклых многогранников, которые называются архимедовы тела. Впрочем, она получилась неполной. Вот зачем другие ученые впоследствии дорабатывали эту теорию.

Описание науки

Геометрией называют раздел математики, который занимается изучением пространственных структур и отношений, а таких их обобщений. Эта наука специализируется на взаимном расположении тел, которое проявляется в виде касания и прилегания друг к другу, размеров объектов и их преобразования.

Геометрическое тело воспринимается как абстракция еще со времен Евклида. Точка является абстракцией, которая связана безграничным уменьшением всех габаритов тела или пределом бесконечного деления. Размеры, размещение и преобразование геометрических фигур регламентируются пространственными отношениями.

При исследовании реальных предметов эта наука концентрируется лишь на их форме и взаимном расположении. При этом плотность, цвет или вес не имеют значения.

Как в дальнейшем развивалась наука

На качественно новый уровень геометрия вышла только через много веков. Это произошло в семнадцатом столетии. Этого удалось добиться благодаря достижениям алгебры, которые накопились к тому моменту. Важный вклад в проект развития геометрии вложил французский математик и философ Рене Декарт. Именно этот ученый предложил новый подход к решению геометрических задач. Он использовал метод координат, связав алгебру с геометрией. Благодаря этому удалось использовать алгебраические методы для решения геометрических задач.

На Руси древнейший труд по арифметике, который дошел до наших дней, был написан еще в 1196 году. Его автором считается новгородский монах Кирик. При этом самая древняя работа, которая дошла до наших дней и включала геометрические сведения, была написана в начале семнадцатого века – скорее всего, в 1607 году. Этот труд получил название «Устав ратных дел». В работе присутствуют правила для решения задач на определение расстояния до объектов. При этом каких-либо теорем или доказательств в работе нет.

В других рукописях, таких как «Книга и письма», присутствуют правила изменения площадей, расчета объемов тел, определения расстояний. Такие правила включают большое количество ошибок и совсем не содержат доказательств.

Популяризации геометрии на Руси противилась церковь. Священнослужители опасались, что с книгами из западных стран в Россию попадет и католицизм. Потому они занимались введением жестких мер против всех, кто занимался математикой. В одном из древнерусских поучений также присутствует фраза: «богомерзостен перед богом всякий, кто любит геометрию».

В конце восемнадцатого века многие ученые столкнулись с мыслью, что доказать пятый постулат Евклида невозможно. Его утверждение отличается сложной формулировкой, потому нередко заменяется аксиомой параллельных прямых. Лобачевский попытался доказать пятый постулат от противного, однако не сумел добиться противоречивых утверждений. В 1826 году ученый заявил о создании новой геометрии, которая отличалась от науки Евклида. Новая теория получила название геометрии Лобачевского. Похожие выводы сделали немецкий ученый Гаусс и венгерский математик Бойяи.

Создание новой геометрии произвело значительное влияние на развитие науки. Геометрия Лобачевского получила широкое применение в естествознании. Также новая наука существенно повлияла на развитие самой геометрии. Это наиболее ярко проявилось в последующем углублении представлений людей о пространстве. До теории Лобачевского считалось, что геометрией окружающего мира может быть исключительно евклидова наука.

Стремительное развитие математики в восемнадцатом веке стало причиной целого ряда важнейших открытий. В частности, немецкий ученый Риман создал новую геометрию. В его науке обобщались сведения из учений Евклида и Лобачевского.

В семидесятые годы девятнадцатого века появилась теория множеств. Согласно этому учению, фигура определяется как множество точек. Этот подход дал возможность посмотреть новым взглядом на геометрию Евклида и проанализировать ее основы. Они подверглись разного рода уточнениям в работах Гильберта.

Где применяется геометрия

В настоящее время геометрия применяется в самых разных отраслях науки – в химии, физике, биологии. Также сложно переоценить ее значение в прикладных сферах знаний. Это, в частности, касается картографии, геодезии, машиностроения. Геометрические методы активно применяются в любых разделах науки и техники, и, безусловно, сама математика не является исключением.

Геометрия представляет собой весьма важную науку, которая зародилась еще в глубокой древности и изначально носила чисто прикладной характер. По мере развития этого учения стало появляться все больше аксиом и теорем. Это позволило изменить представление людей о геометрии и сделать ее более полезной для самых разных сфер человеческой жизни.

Сообщение
появились сначала на
.

Определение инверсии

Присоединим к евклидовой плоскости „бесконечно удалённую» точку . Получим расширенную плоскость, обозначим её через П.

Пусть в плоскости П дана окружность (O,r) с центром O и радиусом r.

Определение. Инверсией относительно окружности (O,r) называют такое отображение П на себя, при котором всякой точке А П, (А≠О, А≠ ) ставится в соответствие точка А’ П так, что выполняются условия:

1) А’ [OA),

2) |OA|·|OA’|= .

Точке О ставим в соответствие точку и, обратно, точке -точку О.

Символом обозначим инверсию относительно окружности (O,r).

Отметим простейшие свойства инверсии, которые вытекают из определения.

. Пусть А П и (A) =A’. Тогда (A’) =A.

Точки А и А’ называются инверсными.

. Инверсия является 1-1 отображением расширенной плоскости П на себя.

. Пусть А П и (A) =A’.

Если |OA|>r, то |OA’| r.

Если |OA|=r, то |OA’|=r.

Таким образом, точки окружности (O,r) и только они, являются при неподвижными.

Легко выполнить построение точки, инверсной данной. Рассмотрим три возможных случая:

2) |OA|>r. Проведём [OA). Через точку А проводим касательную к (O, r). Пусть Т — точка касания. Проведём из Т перпендикуляр на [OA). Основание этого перпендикуляра и есть искомая точка А’. Действительно, из прямоугольного ОТА имеем |OA|·|OA’|= = .

Данная презентация разработана для сопровождения урока-конференции по геометрии, которую целесообразно провести в первый год обучения данному предмету.

Описание разработки

Многие учителя математики сталкивались с тем, что после первых восторгов семиклассников о разделении математики на алгебру и геометрию наступает период, когда часть ребят начинает отдавать явное предпочтение одному из этих двух предметов.

Нередко те, кому хорошо дается алгебра, вдруг начинают испытывать затруднения при решении геометрических задач и применении теорем. И в этот момент учитель должен постараться помочь ученику, и не только с учебной точки зрения, но и в первую очередь с точки зрения мотивации.

Показать, как интересна геометрия, как обширны ее применения, как далеко вглубь времен уходят корни этой науки.

Геометрия (греч. geometria, от ge — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.

В развитии геометрии можно указать четыре основных периода, переходы между которыми обозначали качественное изменение геометрии.

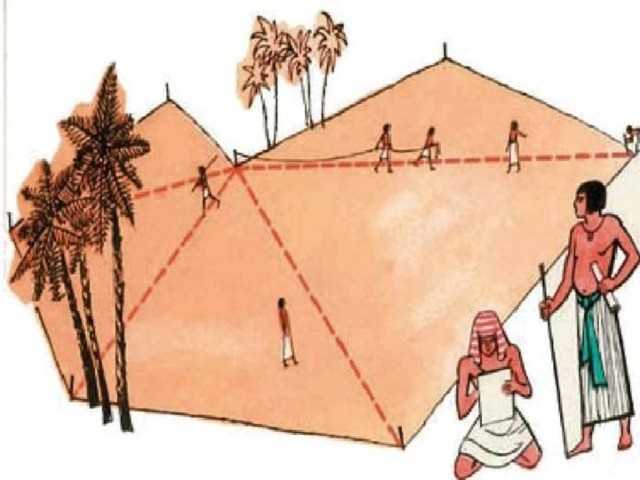
1 период — период зарождения геометрия как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э.

2 период — Геометрия была перенесена в Грецию из Египта в 7 в. до н. э. Здесь геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.

3 период — Возрождение наук и искусств в Европе повлекло дальнейший расцвет геометрии. Принципиально новый шаг был сделан в 1-й половине 17 в.

4 период — В развитии геометрия открывается построением Н. И. Лобачевским в 1826 новой, неевклидовой геометрия.

Василий васильевич розанов философия кратко
Календарно тематическое планирование по русскому языку 4 класс школа россии 2020 2021
Правило чаргаффа это в биологии кратко
Тренинг для начальной школы на тему общения
Нетрадиционные формы работы с родителями в доу в условиях фгос

Евклид

Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птоломея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.

В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.

Ученый гордо ответил: «В геометрии нет царской дороги».

В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида. (Слайд 17).

Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».

IV. Основные понятия планиметрии

Конечно, геометрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.

Мы начинаем изучать планиметрию.

Даже самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших фигур.

Конечно, самая главная — это точка.

Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык непосредственно не с греческого, а через латинский язык.

Точка – результат мгновенного касания, укол

Отсюда же произошел медицинский термин пункция-прокол. Пунктир.

Линия – льняная нить.

Линолеум – первоначально означал промасленное льняное полотно.

Как уже было сказано ранее, все названия геометрических фигур первоначально были названиями конкретных предметов, имеющих форму, более или менее близкую к форме данной фигуры.

V. Повторение известного материала о точках и прямых и их расположении относительно друг друга.

Давайте вспомним, как обозначают на чертеже прямые и точки.

— Прямая безгранична, поэтому на чертеже изображают часть.

— Прямые обозначают двумя заглавными латинскими буквами, соответствующим двум точкам на прямой или одной малой буквой.

— Точки обозначают заглавными латинскими буквами. (Слайд 18).

— Знак Є означает принадлежание, т.е. А Є n означает, что точка А принадлежит прямой n или лежит на ней. И C Є n соответственно, не принадлежит или не лежит. (Слайд 19).

Выполнить задание

Опишите этот рисунок, используя условные обозначения.

VI. Проверка усвоения изученного материала.

1.Практические задания № 1, 2, 3, 7.

2.Учитель выдает кроссворд каждому ученику.

Кроссворд (Слайд 20, 21).