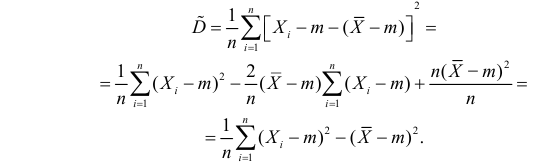Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем Если – результаты независимых наблюдений случайной величины, то в качестве оценки для математического ожидания можно предложить среднее арифметическое наблюдаемых значений 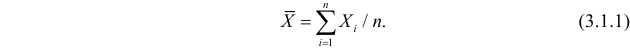
Несмещенность такой оценки следует из равенств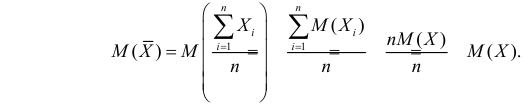
В силу независимости наблюдений 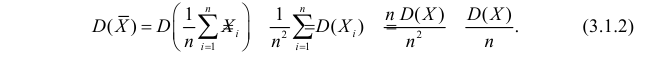
При условии имеем что означает состоятельность оценки .
Доказано, что для математического ожидания нормально распределенной случайной величины оценка еще и эффективна.
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину

Преобразуем величину обозначая для краткости через 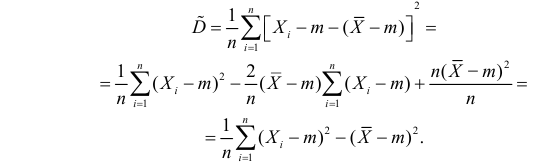
В силу (3.1.2) имеем Поэтому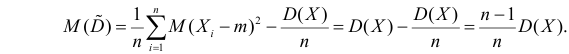
Последняя запись означает, что оценка имеет смещение. Она систематически занижает истинное значение дисперсии. Для получения несмещенной оценки введем поправку в виде множителя и полученную оценку обозначим через
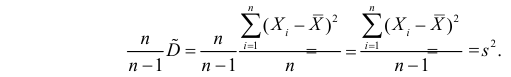
Величина
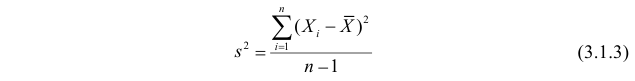
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем 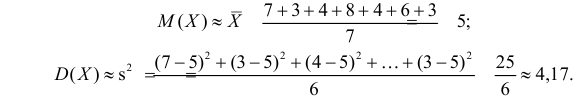
Ответ.
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде: 
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки: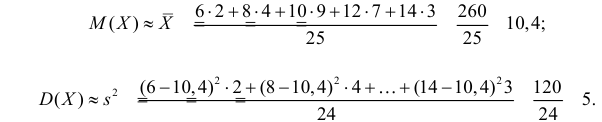
Ответ.
Краткое описание
Чтобы понять смысл условного математического ожидания случайной величины, необходимо изучить ряд правил, а также ознакомится с примерами, дабы в будущем можно было избежать грубых ошибок. Одной из важнейших числовых характеристик дискретной величины является матожидание. Для изучения всех нюансов необходимо ввести понятие системы случайных процессов. Если представить значение в виде графика, то итоговое ожидание будет выступать в виде некоторого центра массы, изображённой на графике фигуры. Для решения классической задачи можно задействовать следующую формулу: Е (х) = Х1О1 + Х1О2 + … + Х n О n.
Расшифровка формулы выглядит следующим образом:
- Е (х) — это точное значение матожидания величины Х.
- Ха — показатель величины случайного типа при конкретном исходе а.
- О — вероятность исхода а.
- n — количество возможных вариантов исходов.
В теории вероятности специалистам удалось доказать, что среднее значение постоянной величины даже после многочисленных испытаний всё равно будет стремиться к матожиданию. В некоторых случаях результат может быть отрицательный. А это значит, что если количество итоговых испытаний слишком велико, то среднее значение обязательно будет равно матожиданию (прогноз среднего значения). Для более тщательного изучения темы специалисты рекомендуют использовать следствие (теорема с небольшим доказательством, которое следует из другой теоремы).
Гораздо проще разобраться в этой теме в том случае, если изучить наглядный пример. Если человек несколько раз бросит самый обычный шестигранный игральный кубик, и будет записывать все выпавшие значения, то при большом количестве испытаний можно получить число 3,5. Аналогичный результат будет достигнут и в том случае, если просчитать матожидание. Подсчёт выглядит следующим образом:
- Р1 = Р2 … = Р6 = 1/6. Это число указывает на вероятность выпадения одной из граней игрального кубика и все они равны, так как у качественного кубика вероятность выпадения каждой грани абсолютно одинаковая.
- Ха = а — формула указывает на то число, которое может выпасть на кубике.
- n = 6 — точное число граней кубика либо количество вариантов.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:
очка
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
, таким образом, математическое ожидание данной игры проигрышно.
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры ![]() Ну, может, только ради развлечения.
Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Пример 5
Случайная величина задана своим законом распределения вероятностей:
Найти , если известно, что . Выполнить проверку.
Есть?
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда: – вероятность промаха.
Составим – закон распределения попаданий при двух выстрелах:
– ни одного попадания. По теореме умножения вероятностей независимых событий:
– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:
– два попадания. По теореме умножения вероятностей независимых событий:
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ
Примечание: можно было использовать обозначения – это не принципиально.
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: Вычислим математическое ожидание: Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: поменяем части местами и проведём упрощения:таким образом:
Выполним проверку:, что и требовалось проверить.
Ответ
(Переход на главную страницу)
Математическое ожидание дискретной случайной величины
Подойдём к понятию математического ожидания. Пусть масса некоторого вещества
распределена между точками оси абсцисс .
При этом каждая материальная точка имеет соответствующую ей массу с вероятностью из .
Требуется выбрать одну точку на оси абсцисс, характеризующую положение всей системы материальных точек,
с учётом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Это
есть среднее взвешенное значение случайной величины X, в которое абсцисса каждой точки
входит с «весом», равным соответствующей
вероятности. Полученное таким образом среднее значение случайной величины X называется её
математическим ожиданием.
Математическим ожиданием дискретной случайной величины называется сумма произведений
всех возможных её значений на вероятности этих значений:
Пример 1. Организована беспроигрышная лотерея.
Имеется 1000 выигрышей, из них 400 по 10 руб. 300 — по 20 руб. 200 — по 100 руб. и 100 —
по 200 руб. Каков средний размер выигрыша для купившего один билет?
Решение. Средний выигрыш мы найдём, если общую сумму выигрышей,
которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая
сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта
среднего выигрыша можно представить и в следующем виде:
С другой стороны, в данных условиях размер выигрыша является
случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с
вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый
средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.
Пример 2. Издатель решил издать новую книгу. Продавать книгу
он собирается за 280 руб., из которых 200 получит он сам, 50 — книжный магазин и 30 — автор. В таблице
дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги.
| Число проданных экземпляров | Вероятность | Затраты |
| 500 | 0,20 | 225000 |
| 1000 | 0,40 | 250000 |
| 2000 | 0,25 | 300000 |
| 3000 | 0,10 | 350000 |
| 4000 | 0,05 | 400000 |
Найти ожидаемую прибыль издателя.
Решение. Случайная величина «прибыль» равна разности доходов от продажи и стоимости затрат.
Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а
затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей
таблице обобщены ожидаемые значения случайной величины — прибыли:
| Число | Прибыль | Вероятность | |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Всего: | 1,00 | 25000 |
Таким образом, получаем математическое ожидание прибыли издателя:
.
Пример 3. Вероятность попадания при одном выстреле .
Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5.
Решение. Из всё той же формулы математического ожидания, которую мы использовали до
сих пор, выражаем — расход снарядов:
.
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения Его параметры и имеют смысл математического ожидания и дисперсии соответственно. Их можно оценить с помощью и В общем случае параметры законов распределения не всегда напрямую связаны со значениями числовых 179 характеристик. Поэтому практический интерес представляет следующая задача.
Пусть случайная величина Х имеет функцию распределения причем тип функции распределения F известен, но неизвестно значение параметра По данным результатов наблюдений нужно оценить значение параметра. Параметр может быть и многомерным.
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности или 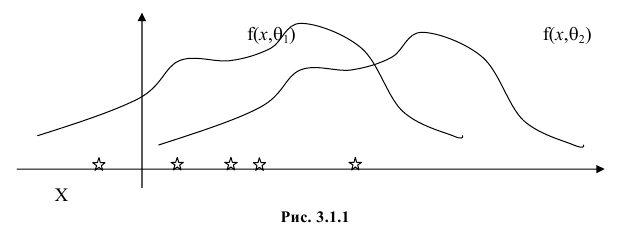
Из рисунка видно, что при значении параметра такие результаты наблюдений маловероятны и вряд ли бы реализовались. При значении же эти результаты наблюдений вполне возможны. Поэтому значение параметра более правдоподобно, чем значение . Такая аргументация позволяет сформулировать принцип наибольшего правдоподобия: в качестве оценки параметра выбирается то его значение, при котором данные результаты наблюдений наиболее вероятны.
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра Обозначим через для непрерывной случайной величины плотность вероятности в точке а для дискретной случайной величины – вероятность того, что Если в независимых наблюдениях реализовались значения случайной величины то выражение ![]()
называют функцией правдоподобия. Величина зависит только от параметра при фиксированных результатах наблюдений При каждом значении параметра функция равна вероятности именно тех значений дискретной случайной величины, которые получены в процессе наблюдений. Для непрерывной случайной величины равна плотности вероятности в точке выборочного пространства
Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое при котором принимает наибольшее значение. Величина будучи функцией от результатов наблюдений называется оценкой наибольшего правдоподобия.
Во многих случаях, когда дифференцируема, оценка наибольшего правдоподобия находится как решение уравнения ![]()
которое следует из необходимого условия экстремума. Поскольку достигает максимума при том же значении , что и , то можно решать относительно эквивалентное уравнение![]()
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция равна произведению, а – сумме, а дифференцировать проще.
Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.