Относительные величины
Интенсивные величины
Интенсивные величины — характеризуют частоту, уровень, интенсивность явления в среде, продуцирующей данное явление. (Например, среда — население, явление — случай заболевания).
Интенсивные показатели в здравоохранении: инвалидность, заболеваемость, смертность, рождаемость.Интенсивные общие показатели — характеризуют явление в целом (общая заболеваемость).Интенсивные специальные (групповые) показатели — характеризуют явление в группе (заболеваемость детей до 1 года).
Экстенсивные величины
Экстенсивные величины — показатели удельного веса, структуры, распределения — характеризуют распределение целого явления на составные части, его внутреннюю структуру, отношение части явления к целому. Выражаются в процентах или долях единицы.
Экстенсивные показатели в медицине: лейкоцитарная формула, структура причин смерти, распределение госпитализированных по срокам поступления и пр.
| Абсолютный размер части явления | ||
| Экстенсивный показатель = | ————————————————— | × основание (100) |
| Абсолютный размер целого явления |
Показатели соотношения
Показатели соотношения характеризуют численное соотношение двух самостоятельных, независимых друг от друга, качественно разнородных совокупностей, сопоставимых только логически.
Например: показатели обеспеченности населения медицинским персоналом (врачами, сестрами), показатели лабораторных исследований на одного врача, число переливаний крови на одного пациента и пр.
| Абсолютный размер явления | ||
| Показатель соотношения = | ————————————————— | × основание (1 000, 10 000) |
| Абсолютный размер среды, не продуцирующей данное явление |
Показатели наглядности
Показатели наглядности применяются с целью более наглядного и доступного сравнения статистических величин. Используются в анализе, когда необходимо отобразить направление процесса, тенденции, не показывая истинных (абсолютных) значений. Показывают сколько процентов составляют анализируемые величины по отношению к сравниваемым.
| Размер явления | ||
| Показатель наглядности = | ————————————————— | × основание (100) |
| Размер такого же явления из ряда сравниваемых, принятый за 100 |
Показатель наглядности
Применяется для анализа однородных чисел и используется когда необходимо «уйти» от показа истинных величин (абсолютных чисел, относительных и средних величин). Как правило, эти величины представлены в динамике.
Для вычисления показателей наглядности одна из сравниваемых величин принимается за 100% (обычно, это исходная величина), а остальные рассчитываются в процентном отношении к ней.
Особенно их целесообразно использовать, когда исследователь проводит сравнительный анализ одних и тех же показателей, но в разное время или на разных территориях.
Пример 1. Рассчитать показатели наглядности для уровней госпитализации в больничные учреждения городов Н. и К. в динамике за 5 лет наблюдения и представить графически.
Таблица 5. Уровень госпитализации в больничные учреждения в городах Н. и К. за 5 лет (на 100 человек населения)
| Показатели | Годы | ||||
| Уровень госпитализации в городе Н. | 24,4 | 22,8 | 21,2 | 20,5 | 20,7 |
| Показатель наглядности, % | 93,44 | 86,9 | 84,0 | 84,7 | |
| Уровень госпитализации в городе К. | 30,0 | 32,0 | 34,0 | 38,0 | 40,0 |
| Показатель наглядности, % | 106,75 | 113,3 | 126,7 | 133,3 |
Решение:
Снижение количества больных, поступивших в стационары будет нагляднее, если приравнять показатель исходного уровня госпитализации в городе Н. (1 год — 24,4) за 100%, а остальные показатели пересчитать в процентах по отношению к нему.
| 24,4 — 100 % 22,8 — X | X = (22,8 х 100) / 24,4 = 93,44% | (показатель наглядности для второго года) |
| 24,4 — 100 % 21,2 — X | X = (21,2 х 100) / 24,4 = 86,9% | (показатель наглядности для третьего года) |
| 24,4 — 100 % 20,5 — X | X = (20,5 х 100) / 24,4 = 84% | (показатель наглядности для четвертого года) |
| 24,4 — 100 % 20,7 — X | X = (20,78 х 100) / 24,4 = 84,8% | (показатель наглядности для пятого года) |
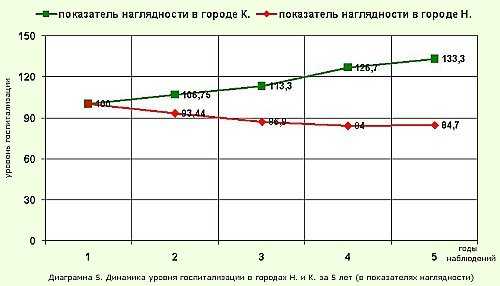
Аналогично рассчитываются показатели наглядности, характеризующие уровень госпитализации в больничные учреждения города К.
Вывод: В динамике за 5 лет наблюдения уровень госпитализации больных в городе Н. снижается, а в городе К. повышается.
Пример 2. Сравнить число коек в больницах А, Б и В и представить графически (табл. 6).
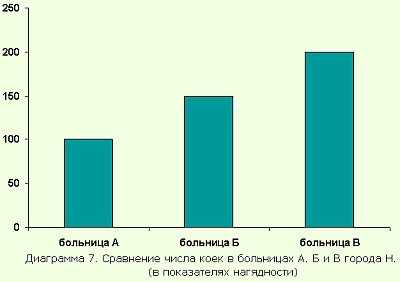
Таблица 6. Число коек в больницах А, Б и В города Н.
| Больница | Число коек | Показатели наглядности, % |
| А | ||
| Б | ||
| В |
Решение:
Принимаем число коек в больнице А (300 коек) за 100%, тогда для » больницы Б показатель наглядности составит:
300 — 100% 450 — X% X = 450 x 100 / 300 = 150%
Аналогично рассчитывается показатель наглядности для больницы В. Он составил 200%.
Вывод: Число коек в больнице Б на 50 %, а в больнице В на 100% больше, чем в больнице А.
Источник
Показатели наглядности: сущность, методика расчета, графика.
Коэффициент наглядности определяет, на сколько процентов или во сколько раз произошло увеличение или уменьшение по сравнению с величиной, принятой за 100%. Используется для характеристики динамики явления. Например, число врачей в 1995 г. по сравнению с числом врачей в 1994 г., принятым за 100% (отношение числа специалистов в данном году к числу специалистов в предыдущем году, умноженное на 100%).
При анализе статистической совокупности используют графические изображения (графические образы — точки, линии, фигуры). Любой график содержит следующие элементы: масштаб, условные обозначения (окраска, штриховка), фигуры, линии, цифры. В медицинской статистике применяют линейные, плоскостные, объемные и фигурные диаграммы. Линейные диаграммы отражают изменение явления в динамике. Сезонный, циклический характер изображают радиальной диаграммой, при этом месяцы года располагают по часовой стрелке. Плоскостные диаграммы (секторные, внутристолбиковые) используют для изображения показателей распределения, доли, процентов, структуры. Ленточные, столбиковые и пирамидальные диаграммы показывают частоту (распространенность, уровень) явления. Фигурные диаграммы, картограммы и картодиаграммы отображают показатели на определенных административных территориях в виде обозначений, фигур.
Вариационные ряды. Виды, определение, составные части, правила.
Для вычисления средних величин необходимо построить вариационный ряд. Вариационные ряды бывают: 1) простыми и взвешенными; 2) сгруппированными и несгруппированными; 3) открытыми и закрытыми; 4) одномодальными и мультимодальными; 5) симметричными и несимметричными; 6) дискретными и непрерывными; 7) четными и нечетными.
Несгруппированные (простые) – составляются при малом числе наблюдений (до 30), сгруппированные – более 30.
Правила составления вариационных рядов:
расположить все варианты по порядку;
суммировать единицы, имеющие одинаковый признак, т.е. найти частоту каждой варианты;
определить количество групп и размер интервала;
разбить весь ряд на группы, используя выбранный интервал и строго соблюдая непрерывность сгруппированного ряда;
дать графическое изображение.
Степень разнообразия (колеблемости) признака в разнородном вариационном ряду можно оценить по коэффициенту вариации (отношение среднего квадратического отклонения к средней арифметической, умноженное на 100%); при вариации менее 10% отмечается слабое разнообразие, при вариации 10—20% — среднее, а при вариации более 20% — сильное разнообразие признака. Если нет возможности сравнить вариационный ряд с другими, то используют правило трех сигм. Если к средней прибавить одну сигму, то этой вычисленной средней соответствует 68,3%, при двух сигмах — 95,4%, при трех сигмах — 99,7% от всех признаков.
Источник
Вариационный ряд
Вариационный ряд — ряд однородных статистических величин, характеризующих один и тот же количественный учётный признак, отличающихся друг от друга по своей величине и расположенных в порядке возрастания или убывания.
Элементы вариационного ряда
- Варианта (V) — числовое значение изучаемого количественного признака
- Частота (p — pars или f — frequency) — частота встречаемость варианты в вариационном ряду.
- Общее число наблюдений (n) — сумма всех частот.
Виды вариационных рядов
- По частоте встречаемости вариант
- Простой — каждая варианта встречается один раз (p = 1)
- Обычный — варианты встречаются более одного раза (p > 1)
- Сгруппированный — варианты объединены в группы по их величине в пределах интервала. Используется при большом числе наблюдений (n > 30) и при большом размахе крайних вариант.
- По типу значений вариант
- Прерывный (дискретный) — состоящий из целых чисел (например, ЧСС, ЧД, число дней лечения).
- Непрерывный — когда значения выражены дробным числом (например, температура тела, уровень белка в крови).
- По числу наблюдений
- Чётный, где n — чётное число
- Нечётный, где n — нечётное число
1.2. Расчет интенсивных показателей
1.2.1. Общий коэффициент смертности =

1.2.2. Коэффициент смертности от болезней системы кровообращения =
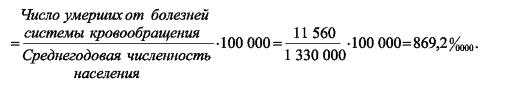
1.2.3. Коэффициент смертности от внешних причин =
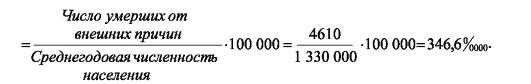
1.2.4. Коэффициент смертности от злокачественных новообразований =
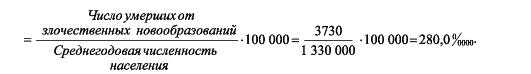
1.2.5. Коэффициент смертности от болезней органов дыхания =
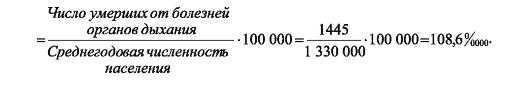
1.2.6. Коэффициент смертности от прочих причин =
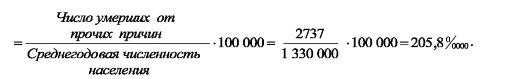
Коэффициент общей смертности населения в некотором субъекте РФ составил 18,1 0 /00, наибольший уровень смертности — от болезней
системы кровообращения (869,2 0 /0000), наименьший — от болезней органов дыхания (108,6 0 /0000). Эти данные превышают аналогичные средние показатели по РФ.
2.2. Полученные данные можно представить в виде столбиковой диаграммы с использованием прикладной компьютерной программы Microsoft Excel (рис. 1.5).
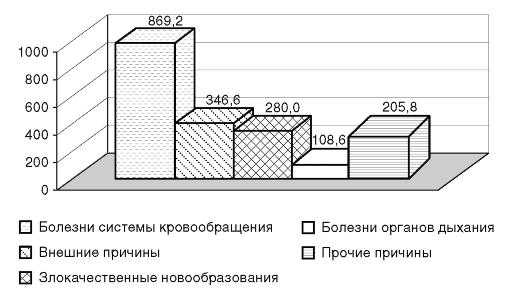
Рис. 1.5. Коэффициент смертности населения от различных причин (на 100 000 населения)






























