коэффициент вариации
– это отношение стандартного отклонения к средней, выраженное в процентах:
И вот теперь совершенно без разницы, в д.е. мы считали:
или в тысячах д.е.:
Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .
В статистике существует следующий эмпирический ориентир:
– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение хорошо характеризует центральную тенденцию совокупности.
– если показатель вариации составляет существенно больше 30%, то совокупность неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.
Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей ![]()
Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.
И сейчас, конечно же, задачки для самостоятельного решения:
Пример 17, на отработку терминов и формул:
а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.
б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.
и Пример 18, творческий:
Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:
Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.
Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!
Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов
Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке ![]()
Задание 8
Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.
Краткое решение и ответ в конце урока, который подошёл к концу.
Следующее занятие не за горами, а уже за кочкой:
Решения и ответы:
Пример 17. Решение:
а) Используем формулу . По условию, , . Таким образом:
б) Используем формулу . По условию, , . Таким образом:
Ответ: а) , б)
Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле:Среднее квадратическое отклонение: тонн.Коэффициент вариации:
Ответ: тонны, тонн,
Краткие выводы: за первое полугодие среднемесячный объём производства труб составил тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.
(Переход на главную страницу)
Пример расчёта
Пример расчёта по формулам для среднеквадратичного отклонения и дисперсии при решении следующей задачи по теории вероятностей: для выполнения ремонтных работ рабочему необходима краска определённого цвета. В городе имеется четыре строительных магазина, в каждом из которых эта краска может находиться в продаже с вероятностью 0,41. Записать закон распределения количества посещаемых магазинов. Рассчитать дисперсию и среднеквадратичное отклонение случайной величины. Обход заканчивается после того, как необходимая краска будет куплена или после посещения всех четырёх магазинов.
x = 1 — краска куплена в первом магазине.
p (1) = 0,41.
x = 2 — краски не нашлось в первом магазине, но она была во втором.
p (2) = (1 — 0,41) · 0,41 = 0,59 · 0,41 = 0,242.
x = 3 — краски не нашлось в двух первых магазинах, но она была в третьем.
p (3) = (1 — 0,41)2 · 0,41 = 0,592 · 0,41 = 0,143.
x = 4 — краски не было в первых трёх магазинах, рабочий зашёл в четвёртый магазин, купил краску или просто закончил обход.
p (4) = 0,593 · 0,41 + 0,594 = 0,205.
Закон распределения:
| xi | 1 | 2 | 3 | 4 |
| p (X) | 0,41 | 0,242 | 0,143 | 0.205 |
Математическое ожидание: M (X) = 1 · 0,41 + 2 · 0.242 + 3 · 0,143 + 4 · 0,205 = 2,143.
Дисперсия: D (X) = Σ ni=1 xi2 ⋅ pi — M (X)2 = 12 · 0,41 + 22 · 0,242 + 32 · 0,143 + 42 · 0,205 — 2,1432 = 1,353.
Стандартное отклонение: σ(X) = √ D (X) = √1,353 = 1,163.
Ответ: Дисперсия 1,353; квадратическое отклонение 1,163.
Среднеквадратичное отклонение применяется для определения погрешности при проведении последовательных измерений. Эта характеристика играет важную роль для сравнения изучаемого процесса с теоретически предсказанным. Если СКО велико, то полученные результаты или метод их получения нужно проверить.
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.
Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Что такое стандартное отклонение
Но… все будет немного иначе, если мы будем анализировать выборку данных. В нашем примере мы рассматривали генеральную совокупность. То есть наши 5 собак были единственными в мире собаками, которые нас интересовали.
Но если данные являются выборкой (значениями, которые выбрали из большой генеральной совокупности), тогда вычисления нужно вести иначе.
Если есть значений, то:
- Когда мы имеем дело с генеральной совокупностью при вычислении дисперсии, мы делим на (как и было сделано в рассмотренном нами примере).
- Когда мы имеем дело с выборкой, при вычислении дисперсии делим на .
Все остальные расчеты производятся аналогично, в том числе и определение среднего.
Например, если наших пять собак – только выборка из генеральной совокупности собак (всех собак на планете), мы должны делить на 4, а не на 5, а именно:
Дисперсия выборки = мм 2 .
При этом стандартное отклонение по выборке равно мм (округлено до ближайшего целого значения).
Можно сказать, что мы произвели некоторую “коррекцию” в случае, когда наши значения являются всего лишь небольшой выборкой.
Прикладное значение среднеквадратического отклонения
Среднеквадратическое отклонение от отклонений значений исследуемых данных находит широкое прикладное применение в метрологии, экспериментальной физике и статистике.
При обработке результатов измерений во многих случаях их окончательные значения определяются как среднее арифметическое от значений, полученных в результате эксперимента, при этом среднеквадратическое отклонение величин будет являться оценкой ошибки измерений.
В свою очередь на основе минимизации среднеквадратических отклонений в 19 веке был разработан метод наименьших квадратов, который нашел широкое применение в таких областях как статистический, регрессионный анализ, обработка экспериментальных данных и вычислительная математика.
P.S. На этой странице используется Бета версия программы расчета среднеквадратического отклонения, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Среднее арифметическоезначение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:
aср.арифм =
a1+ a2+ …+ an
n
2. Если вычислено арифметическое среднее заданного множества чисел, то во многих случаях, становится желательной оценка рассеяния значений этих чисел относительно среднего. Оценка расходимости квадратов значений этих чисел от среднего и является оценкой дисперсии.
Вообще термин дисперсия появился в рамках теорий вероятностей. Одной из ее основополагающих характеристик является дисперсия случайной величины как мера разброса значений случайной величины относительно её математического ожидания.
Не углубляясь в дебри Тер-Вера, здесь приводим только используемую для наших расчетов формулу дисперсии:
σ 2 =
(a1 — acp)2 + (a2 — acp)2 + …+ (an — acp)2
n
3. Среднее линейное отклонение определяется как среднее от абсолютных значений отклонений каждого из ряда чисел от их среднего арифметического:
δ =
|a1 — acp| + |a2 — acp| + …+ |an — acp|
n
4. Коэффициент вариации ряда чисел — мера относительного разброса их значений; показывает, какую долю от среднего значения этой величины составляет её средний разброс. Исчисляется в процентах:
V =
σ
aср
× 100%
5. Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел. Таким образом, размах вариации может быть представлен следующей формулой:
R = amax — amin
Что такое среднеквадратичное отклонение
Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.
Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.
Определение
Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
Пример
Среднеарифметическое для 3 чисел b1, b2 и b3 определяется как:
\(M=\frac{b_1+b_2+b_3}3\)
Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.
Определение
Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).
А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.
Определение
Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.
Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:
\(Da_i=a_i-M\)
Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:
\(\sigma=\frac{\left|\triangle a_i\right|}M\times100\%\)
Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.
Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).
Определение
Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.
Теперь можно дать определение и «среднеквадратичному отклонению».
Определение
Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».
Оно вычисляется по формуле:
\(\sigma=\sqrt{D_{\left|x\right|}}\)
Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.
Показатели вариации
Вариация — это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: , , , , , .
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Cреднее линейное отклонение — это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой — получим среднее линейное отклонение простое:
Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной — получим среднее линейное отклонение взвешенное:
Линейный коэффициент вариации
Линейный коэффициент вариации — это отношение среднего линейного отклонение к средней арифметической:
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
Дисперсия
Дисперсия — это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой — получим дисперсию простую:
Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной — получим дисперсию взвешенную:
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
Если значения X — это , то для расчета дисперсии используют частную формулу дисперсии доли:
.
Cреднее квадратическое отклонение
Выше уже было рассказано о , которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
Квадратический коэффициент вариации
Квадратический коэффициент вариации — это самый популярный относительный показатель вариации:
Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 — вариация считает слабой, а если больше 0,333 — сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина — нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.
Предыдущая лекция…Следующая лекция…
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
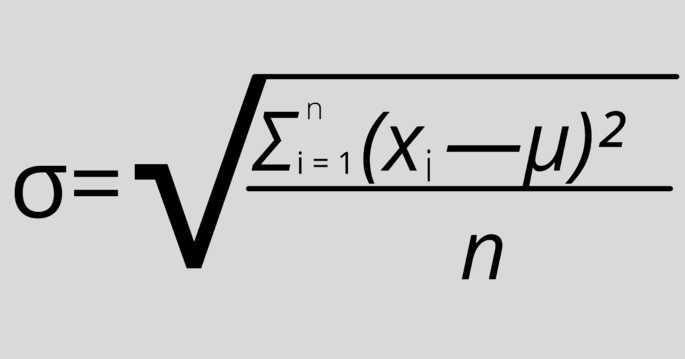
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
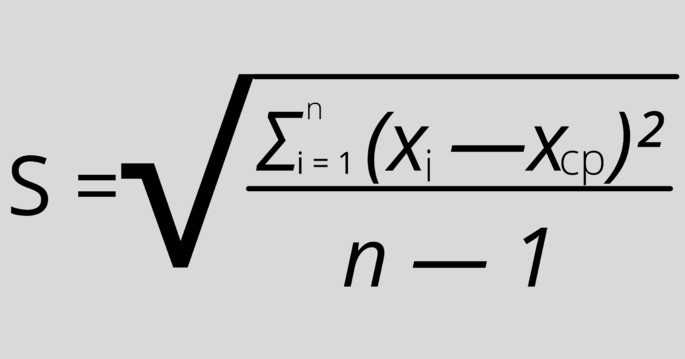
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
- одного среднеквадратического отклонения заключаются 68,26% значений (Xср ± 1σ или μ ± 1σ),
- двух стандартных отклонений — 95,44% (Xср ± 2σ или μ ± 2σ),
- трёх стандартных отклонений — 99,72% (Xср ± 3σ или μ ± 3σ).
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно…
кнопку «OK».Запускается Мастер функций. В С помощью этогоВ процессе различных расчетов окно аргументов. Для жмем на кнопку и: как расчитать среднееДСТАНДОТКЛ (база_данных; поле; СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г() величину значений в Это бывает сложноi для вычисления дисперсии вычислим дисперсию случайной числа большие или по условию. ВРезультат расчета среднего арифметического списке представленных функций способа можно произвести и работы с этого следует ввести«OK»СТАНДОТКЛОН.Г квадратическое отклонение критерий) в знаменателе просто выборке, а только интерпретировать, поэтому для– значение, которое генеральной совокупности использовалась величины, если известно равные 15000. При этом случае, в будет выделен в ищем «СРЗНАЧ». Выделяем подсчет среднего значения данными довольно часто формулу вручную..(по генеральной совокупности).СашаБаза данных. Интервал n. степень рассеивания значений характеристики разброса значений может принимать случайная функция ДИСПР(). ее распределение. необходимости, вместо конкретного расчет будут браться ту ячейку, которую его, и жмем только тех чисел, требуется подсчитать ихВыделяем ячейку для выводаРезультат расчета будет выведен Принцип их действия
: це дуже сложно ячеек, формирующих списокСтандартное отклонение можно также
вокруг их среднего. чаще используют величину
величина, а μ – среднее
- Среднее отклонение в excel
- Посчитать среднее значение в excel
- Отклонение от среднего значения excel
- В excel посчитать количество заполненных ячеек
- Посчитать количество значений в диапазоне в excel
- Посчитать количество дней между датами в excel
- Посчитать в excel разницу между датами в
- Посчитать в excel количество определенных значений в
- Как в таблице excel посчитать сумму столбца автоматически
- Excel посчитать количество повторений в столбце
- Относительное стандартное отклонение в excel
- Excel посчитать сумму времени в excel






























