Дисперсия — свойства, виды и формулы

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где xi – значение из ряда;

fi – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Как найти данную дисперсию? По формуле:

где k – количество групп;

nj – элементов в группе с индексом j.

Внутригрупповая дисперсия

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

https://youtube.com/watch?v=RgaXFRSOELI

Групповая и межгрупповая вариации. Правило сложения дисперсии

Если
статистическая совокупность разбита
на группы или части по изучаемому
признаку, то для такой совокупности
могут быть исчислены следующие виды
дисперсии: групповые (частные), средне
групповые (частных), и межгрупповая.

Общая
дисперсия
–
отражает вариацию признака за счет всех
условий и причин, действующих в данной
статистической совокупности.

Групповая
дисперсия
—
равна среднему квадрату отклонений
отдельных значений признака внутри
группы от средней арифметической этой
группы, называемой групповой средней.
При этом групповая средняя не совпадает
с общей средней для всей совокупности.

Групповая
дисперсия отражает вариацию признака
только за счет условий и причин,
действующих внутри группы.

Средняя
групповых дисперсий

— определяется как среднее взвешенное
арифметическое из дисперсий групповых,
причем весами являются объемы групп.

Межгрупповая
дисперсия
—
равна среднему квадрату отклонений
групповых средних от общей средней.

Межгрупповая
дисперсия характеризует вариацию
результативного признака за счет
группировочного признака.

Между
рассмотренными видами дисперсий
существует определенное соотношение:
общая дисперсия равна сумме средней
групповой и межгрупповой дисперсии.

Это
соотношение называется правилом сложения
дисперсии.

Свойства дисперсии

Свойство 1. Дисперсия постоянной величины A равна (нулю).

D(A) = 0

Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.

D(AX) = А2 D(X)

Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.

D(A + X) = D(X)

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

D(X+Y) = D(X) + D(Y)

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.

D(X-Y) = D(X) + D(Y)

2.2.10 Полная дисперсия

В общем случае полная дисперсия в оптическом волокне должна определяться в соответствии с выражением 2.9:

1. В ОМ ОВ модовая дисперсия отсутствует, так как по такому волокну распространяется только одна мода НЕ₁₁ или, как отмечалось ранее, две моды в двух разных состояниях поляризации. В обычных условиях работы ОМ ОВ поляризационная дисперсия достаточно мала и поэтому при расчёте полной дисперсии ею можно пренебречь. Другими словами, расширение импульсов в ОМ ОВ определяется хроматической дисперсией в пределах низшей моды. Тогда полная дисперсия в ОМ ОВ может быть представлена в общем виде выражением:

Волноводная дисперсия τ_вол мала, и ею можно пренебречь:

Таким образом в ОМ ОВ материальная дисперсия является основным видом дисперсии.

2. В ММ ОВ, так же мала по величине волноводная дисперсия τ_вол, поэтому ею пренебрегают при определении полной дисперсии. Исходя из этого, полная дисперсия ММ ОВ может быть представлена в общем виде выражением:

В ММ ОВ со ступенчатым профилем показателя преломления τ_мод доминирует над τ_мат (τ_мод>τ_мат) и модовая дисперсия является основным видом дисперсии:

3.В градиентном ММ ОВ – наоборот τ_мат доминирует над τ_мод (τ_мат>τ_мод). Это объясняется тем, что в градиентном многомодовом ММ ОВ τ_мод уменьшается за счёт выравнивания времени распространения различных мод и поэтому материальная дисперсия является основным видом дисперсии:

Сравнивая дисперсионные характеристики различных волокон, можно отметить, что наилучшими показателями обладают ОМ ОВ, а наиболее сильно дисперсия проявляется в ММ ОВ со ступенчатым профилем показателя преломления.
В световодах с градиентным профилем показателя преломления и одномодовых световодах уширение импульса вызывается главным образом материальной дисперсией, обусловленной зависимостью показателя преломления материала световода от длины волны.
Во многих случаях модовая дисперсия не играет никакой роли при конструировании волоконных систем: быстродействие слишком мало или расстояния незначительны.

2.2.6 Материальная дисперсия

Напомним, что материальная дисперсия – это дисперсия, обусловленная зависимостью показателя преломления от длины волны:

Волны различной длины движутся с различными скоростями по ВС, даже в одной и той же моде. Как известно, показатель преломления равен:

где c– скорость света в вакууме; υ– скорость света в веществе.
Поскольку волны различной длины движутся с разной скоростью, то величина скорости υ в этом уравнении изменяется для каждой длины волны. Таким образом, показатель преломления изменяется в зависимости от длины волны. Дисперсия, связанная с этим явлением, называется материальной (молекулярной) дисперсией, поскольку зависит от физических свойств вещества волокна. Материальная дисперсия определяется электромагнитным взаимодействием волны со связанными электронами материала среды, которое носит, как правило, нелинейный характер. Уровень материальной дисперсии зависит от двух факторов:

• диапазона длин волн света, вводимого в волокно;
• центральной рабочей длины волны источника.

Рассмотрим каждый фактор подробнее.
1. Как правило, источник не может излучать одну длину волны; он излучает спектр волн. Диапазон длин волн Δλ называется спектральной шириной источника. Светоизлучающий диод (СИД) характеризуется большей спектральной шириной Δλ≈35нм, а лазерный диод (ЛД) – меньшей: от 2 до 3нм – многомодовый и от 0,01 до 0,02нм – одномодовый.
2. В области 850нм более длинные волны (более красные) движутся быстрее по сравнению с более короткими (более синими) длинами волн (рисунок 2.9). Длина стрелок соответствует скорости волн, следовательно, более длинная стрелка соответствует более быстрому движению. Волны длиной 850нм движутся быстрее по стеклянному волокну, чем волны длиной 845нм.

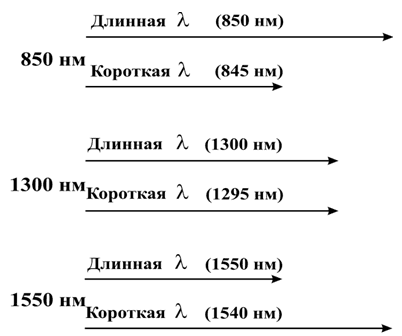Рисунок 2.9 – Скорости распространения света разной длины волны

В выражение для материальной дисперсии одномодового волокна входит дифференциальная зависимость показателя преломления от длины волны:

где Δλ – ширина спектра источника излучения;l – длина световода;λ – длина волны излучения;c – скорость света в вакууме;n₁ – показатель преломления сердцевины; – удельная материальная дисперсия (определяется экспериментальным путём).

Удельная материальная дисперсия измеряется в пикосекундах на километр длины световода и на нанометр ширины спектра источника: [nc/(км•нм)] .
Зависимость удельной материальной дисперсии от длины волны приведена на рисунке 2.10.

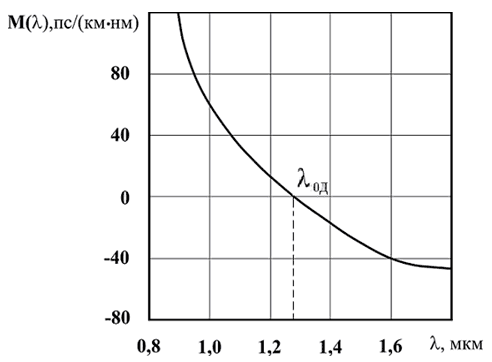Рисунок 2.10 – Зависимость удельной материальной дисперсии объёмного кварцевого стекла от длины волны

Интересно отметить, что в объёмном кварцевом стекле в диапазоне длин волн 1000 – 1600нм М(λ) почти линейно уменьшается от плюс 70 до минус 40пс/(км•нм), принимая нулевое значение на длине волны примерно 1300нм, а точнее 1270нм.
Длина волны, при которой удельная материальная дисперсия М(λ) обращается в ноль, называется длиной волны нулевой дисперсии λ_0Д для объёмной среды.
В области длин волн менее λ_0Д материальная дисперсия положительная – более красные волны опережают более синие и прибывают раньше. В области длин волн больше λ_0Д материальная дисперсия отрицательная – более красные волны отстают и прибывают позднее.
Из описанного ясно, что для уменьшения дисперсии нужно, с одной стороны, при выборе источника переходить от оптических источников типа СИД к ЛД, а. c другой стороны, необходимо переходить от источников с длинами волн порядка 850нм к источникам с длинами волн порядка 1300нм для использования эффекта нулевой дисперсии.

2.2.7 Волноводная дисперсия

Волноводная дисперсия – это дисперсия реальных световодов, отличающаяся от дисперсии объёмной среды по причине наличия волноводной структуры, изменяющей эффективный показатель преломления моды. Когда растёт длина волны, то большая часть поля заходит в оболочку и меняет показатель преломления среды. Изменяя эффективный показатель преломления среды можно менять дисперсию.
Волноводная дисперсия обусловлена зависимостью эффективного показателя преломления от длины волны, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра

где Δλ – ширина спектра источника излучения;l – длина световода;n₁ – показатель преломления сердцевины;Δ – относительный показатель преломления;c – скорость света в вакууме;λ – длина волны излучения; – удельная волноводная дисперсия.
Типичная зависимость удельной волноводной дисперсии кварцевого одномодового волокна от длины волныприведена на рисунке 2.11.

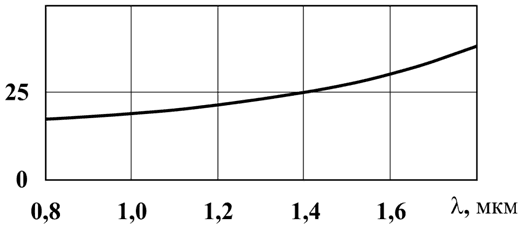Рисунок 2.11 – Зависимость удельной волноводной дисперсии кварцевого волокна от длины волны

Как видно из рисунка 2.11, удельная волноводная дисперсия N(λ) всегда больше нуля, т. е. положительная.
Вклад волноводной дисперсии зависит от:

• радиуса сердцевины;
• разности показателей преломления сердцевины и оболочки;
• числа оболочек.

В многомодовых ОВ волноводная дисперсия относительно мала по величине.

2.2.1 Дисперсия

Оптический сигнал, распространяясь по волокну, не только затухает, но и искажается за счёт дисперсии различного рода.
Под дисперсией σ в оптике понимают зависимость фазовой скорости световых волн от частоты υ_ф=υ_ф(ω). Это же относится и к показателю преломления n=n(ω). Величина и характер дисперсии определяется как:

В этом смысле дисперсия носит название хроматической дисперсии, подчёркивая факт разложения света на его спектральные составляющие. Дисперсия называется нормальной, если n увеличивается с увеличением частоты ω и аномальной, если n уменьшается с увеличением ω. Зависимость фазовой скорости от ω для нормальной и аномальной дисперсий – обратная.

Смещение

Аналогично тому, как производится выборка из генеральной совокупности, дата-сайентисты из готового датасета выделяют тренировочный набор. Именно на этой «выборке второго порядка» модель учится делать предсказания.

Прочитайте нашу статью о создании простой модели машинного обучения. Она предсказывает город, в который вероятнее всего поедет турист, на основании его возраста, пола, места жительства, дохода и транспортных предпочтений. Такая рекомендательная система на минималках.

Смещение происходит, когда модель недооценивает или переоценивает какой-либо параметр. Представим, что модель из статьи выше отправляет всех краснодарцев в Париж — независимо от их дохода, предпочтений и других параметров. В этом случае мы скажем, что модель переоценивает значение параметра «Город проживания».

Чаще всего причиной смещения являются:

• неправильный сбор данных в датасет: например, в него попали только краснодарцы — любители Парижа;
• неправильное формирование тренировочного набора из датасета;
• неправильное измерение ошибок.

Когда мы неверно собираем данные, говорят о систематической ошибке отбора. Например, в прошлом веке многие считали, что во Вселенной больше голубых галактик, — впечатление возникало потому, что плёнка была более чувствительна к голубой части спектра.

О доброте дельфинов мы знаем только от спасённых ими людей. Фото: Pixabay

Другая ошибка — ошибка меткого стрелка — происходит, когда мы вольно или невольно отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадём.

Причин, вызывающих смещение, так много, что Марк Твен заметил: «Существует три вида лжи: ложь, наглая ложь и статистика». Например:

• Эффект низкой/высокой базы. Если в финансовом отчёте найти самый низкий показатель прибыли, то на его фоне любой другой результат будет выглядеть как достижение. И наоборот: если хотите показать, что ученик перестал прогрессировать, сравнивайте текущие оценки с его лучшими результатами за все годы обучения.
• Сокращение рассматриваемого периода. Если хочется доказать, что рекламная кампания не приносит результатов, надо просто найти период, когда деньги уже потрачены, а эффекта ещё нет. И рассматривать только его.
• Исключение из выборки. Если вы измеряете результативность методики снижения веса, то можно выкидывать из выборки участников, которые отказались от методики, не дойдя до конца. Это существенно «повысит» эффективность методики.
• Ну и, конечно же, классика: «Интернет-опрос населения показал, что 100% населения пользуются интернетом».

Эти и другие ошибки смещения трудно выявить статистическими методами, поэтому нужно стараться избежать их до того, как вы начнёте сбор данных.

Если пить «Боржоми» уже поздно (датасет уже сформирован), обязательно спросите себя: «Не смещены ли мои данные?» — а они наверняка смещены, «Куда и почему они смещены?» и «Можно ли с этим жить?»

Виды дисперсии

Общая
дисперсия
измеряет
вариацию признака по всей совокупности
в целом под влиянием всех факторов,
обуславливающих эту вариацию. Она
равняется среднему квадрату отклонений
отдельных значений признака х от общего
среднего значения х и может быть
определена как простая дисперсия или
взвешенная дисперсия.

Внутригрупповая
дисперсия

характеризует
случайную вариацию, т.е. часть вариации,
которая обусловлена влиянием неучтенных
факторов и не зависящую от признака-фактора,
положенного в основание группировки.
Такая дисперсия равна среднему квадрату
отклонений отдельных значений признака
внутри группы X от средней арифметической
группы и может быть вычислена как простая
дисперсия или как взвешенная дисперсия.

Таким
образом, внутригрупповая
дисперсия измеряет
вариацию
признака внутри группы и определяется
по формуле:

где
хi — групповая средняя;
ni
— число единиц в группе.

Например,
внутригрупповые дисперсии, которые
надо определить в задаче изучения
влияния квалификации рабочих на уровень
производительности труда в цехе
показывают вариации выработки в каждой
группе, вызванные всеми возможными
факторами (техническое состояние
оборудования, обеспеченность инструментами
и материалами, возраст рабочих,
интенсивность труда и т.д.), кроме отличий
в квалификационном разряде (внутри
группы все рабочие имеют одну и ту же
квалификацию).

Средняя
из внутри групповых дисперсий отражает
случайную вариацию,
т. е. ту часть вариации, которая происходила
под влиянием всех прочих факторов, за
исключением фактора группировки. Она
рассчитывается по формуле:

Межгрупповая
дисперсия
характеризует
систематическую вариацию результативного
признака, которая обусловлена влиянием
признака-фактора, положенного в основание
группировки. Она равняется среднему
квадрату отклонений групповых средних
от общей средней. Межгрупповая дисперсия
рассчитывается по формуле:

Дисперсия
в статистике определяется как среднее
квадратическое отклонение индивидуальных
значений признака в квадрате от средней
арифметической. Распространенный способ
расчета квадратов отклонений вариантов
от средней с их последующим усреднением.

В
экономически-статистическом анализе
вариацию признака принято оценивать
чаще всего с помощью среднего
квадратического отклонения, оно
представляет собой корень квадратный
из дисперсии.

(3)

Характеризует
абсолютную колеблемость значений
варьирующего признака выражается в тех
же единицах измерения, что и варианты.
В статистике часто возникает необходимость
сравнения вариации различных признаков.
Для таких сравнений используется
относительный показатель вариации,
коэффициент вариации.

Свойства
дисперсии:

1)если
из всех вариант вычесть какое-либо
число, то дисперсия от этого не изменится;

2)
если все значения вариант разделить на
какое-либо число b,
то дисперсия уменьшится в b^2
раз, т.е.

3)
если исчислить средний квадрат отклонений
от какого-либо числа с неравного средней
арифметической, то он будет больше
дисперсии
.
При этом на вполне определенную величину
на квадрат разности между средней
величиной поc.

Дисперсию
можно определить как разницу между
средним квадратом и средней в квадрате.

Коэффициент осцилляции

Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.

Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. 

Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.

2.2.11 Ширина полосы пропускания

Полоса пропускания – это мера способности волокна передавать определённый объём информации в единицу времени.
Чем шире полоса пропускания, тем выше скорость передачи волокна. Например, одно волокно с градиентным профилем показателя преломления может легко передавать 500млн. бит информации в секунду (500Мбит/с).
Поскольку модовая дисперсия не зависит от длины волны излучения в многомодовых изделиях, многие производители волокна и оптического кабеля не используют в спецификации дисперсию. Вместо неё они указывают произведение информационной ширины полосы пропускания Δf на длину волокна l, выраженное в мегагерцах на километр (рисунок 2.14).

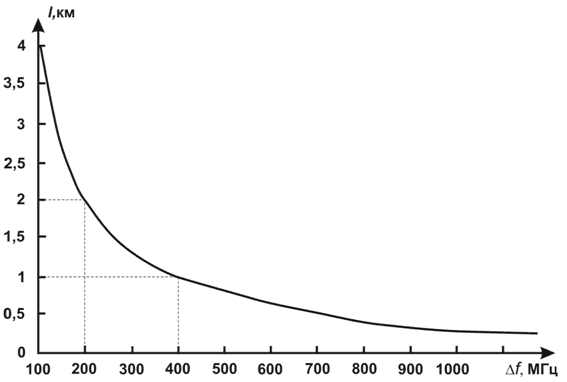Рисунок 2.14– Зависимость длины линии передачи от ширины полосы пропускания для ОВ с параметром B=400МГц·км

Полоса пропускания B=400МГц·км означает возможность передачи сигнала в полосе 400МГц на расстояние 1км. Это также означает, что произведение максимальной частоты сигнала на длину линии передачи может быть меньше или равно 400МГц·км. Другими словами, при одной и той же дисперсии можно передавать сигнал более низкой частоты на большее расстояние или более высокой частоты на меньшее расстояние, как показано на рисунке 2.14.
В зависимости от ППП и длины волны излучения сигнала многомодовые волокна имеют различную полосу пропускания сигнала:

• при ступенчатом ППП – полоса пропускания 20МГц⋅км;
• при градиентном ППП – полоса пропускания 160МГц⋅км для λ=0,85мкм и 500МГц⋅км для λ=1,3мкм.

Рабочая полоса частот (полоса пропускания) в ВОК лимитируется дисперсией ОВ. Полоса пропускания ММ ОВ имеет верхнюю границу 500–800МГц⋅км.
На рисунке 2.15 показан характер изменения дисперсии τ и полосы пропускания Δf ОВ в зависимости от длины линии l.

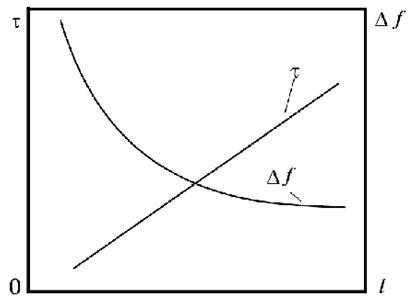Рисунок 2.15 – Дисперсия τ и полоса пропускания Δf ОВ от длины линии

Снижение из-за дисперсии величины Δf до допустимого значения лимитирует дальность передачи по ВОК. Таким образом, полоса частот Δf и дальность передачи l взаимосвязаны.
В ОМ ОВ спецификация дисперсии необходима. Для заданного ОМ ОВ дисперсия в основном определяется спектральной шириной источника: чем шире полоса излучения источника, тем больше дисперсия.

Предыдущая

Оглавление

Следующая

коэффициент вариации

– это отношение стандартного отклонения к средней, выраженное в процентах:

И вот теперь совершенно без разницы, в д.е. мы считали:

или в тысячах д.е.:

Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .

В статистике существует следующий эмпирический ориентир:

– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение  хорошо характеризует центральную тенденцию совокупности.

– если показатель вариации составляет существенно больше 30%, то совокупность неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.

Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей

Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.

И сейчас, конечно же, задачки для самостоятельного решения:

Пример 17, на отработку терминов и формул:

а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.

б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.

и Пример 18, творческий:

Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:

Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.

Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!

Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов

Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке

Задание 8

Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.

Краткое решение и ответ в конце урока, который подошёл к концу.

Следующее занятие не за горами, а уже за кочкой:

Решения и ответы:

Пример 17. Решение:

а) Используем формулу . По условию, , . Таким образом:

б) Используем формулу . По условию, , . Таким образом:

Ответ: а) , б)

Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле:Среднее квадратическое отклонение: тонн.Коэффициент вариации:

Ответ:  тонны,  тонн,

Краткие выводы: за первое полугодие среднемесячный объём производства труб составил  тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.

(Переход на главную страницу)

2.2.2 Воздействие дисперсии на сигнал

При прохождении импульсных сигналов по световоду дисперсия приводит, как было сказано выше, к уширению импульса (рисунок 2.5).

а – входные импульсы; б – выходные импульсы
Рисунок 2.5 – Уширение импульса из-за дисперсии в волоконном световоде

Она определяется как квадратичная разность длительности импульсов на выходе и входе световода длиной l, получаемой на половине высоты импульса, и измеряется в пикосекундах .

Предел пропускной способности (скорости передачи информации, информационной полосы пропускания) волоконного световода определяется тем, насколько близко могут располагаться кодирующие информацию соседние импульсы без взаимного перекрытия и, следовательно, без возникновения межсимвольных помех. Большие значения дисперсии приводят к ошибкам декодирования вследствие перекрытия импульсов цифрового оптического сигнала.

Уширение импульса определяет полосу частот передаваемого сигнала Δf (скорость передачи информации) следующим образом:

Например, значения дисперсии τ=2–5пс соответствуют полосе частот Δf=500–200МГц.
Дисперсия также ограничивает длину регенерационного участка, так как уширение импульса пропорционально длине линии. В конечном итоге может возникнуть ситуация, когда соседние импульсы перекрывают друг друга.

Что такое среднеквадратичное отклонение

Рассматривая какие-либо величины или их изменения, используют такие критерии как среднеарифметическая величина и ее отклонение. Различные понятия позволяют оценить разброс измеряемой величины и ее отклонение. К ним относится абсолютная погрешность, которая показывает насколько каждая конкретная величина отличается от среднего значения. Но так как сумма всех абсолютных погрешностей равна нулю, то этот критерий не позволяет показать разброс измеряемых величин. И для решения этой задачи был введен новый показатель — среднее квадратичное отклонение.

Для того чтобы объяснить его смысл необходимо вспомнить некоторые основные математические понятия.

Определение

Средней величиной или средним арифметическим называется число, полученное в результате деления суммы всех величин на их количество.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Пример

Среднеарифметическое для 3 чисел b₁, b₂ и b₃ определяется как:

\(M=\frac{b_1+b_2+b_3}3\)

Со средней величиной непосредственно связана и другая характеристика — математическое ожидание.

Определение

Значение среднего арифметического некоторого множества при стремлении его членов к бесконечности называется математическим ожиданием (М).

А оценкой математического ожидания является среднее арифметическое определенного числа измерений изучаемой величины.

Определение

Вариантой или абсолютной погрешностью называется разность измеряемой величины со средним значением.

Она обозначается греческой буквой D. Для того чтобы найти варианту единичного измерения ai следует отнять от ее значение среднее арифметическое:

\(Da_i=a_i-M\)

Также для оценки единичного измерения используется и относительная погрешность, значение которой выражается в процентах. Ее вычисление проводят по формуле:

\(\sigma=\frac{\left|\triangle a_i\right|}M\times100\%\)

Относительная погрешность каждой величины позволяет отбросить из вариации измерений значения с очень большой погрешностью и проводить дальнейший анализ только величин с незначительной относительной погрешностью.

Характеристикой распределения значений некоторой измеряемой величины является дисперсия (D).

Определение

Дисперсией называется среднее арифметическое квадратов всех абсолютных погрешностей.

Теперь можно дать определение и «среднеквадратичному отклонению».

Определение

Значение корня квадратного из дисперсии случайной величины называется среднеквадратичным отклонением и обозначается «ϭ».

Оно вычисляется по формуле:

\(\sigma=\sqrt{D_{\left|x\right|}}\)

Единицей измерения среднеквадратического отклонения является единица измерения исследуемой величины. Данный критерий используется при измерении линейной функции, статической проверки гипотезы, расчете стандартной ошибки среднего арифметического, а также при построении доверительных интервалов.

Семплирование

Предположим, вам требуется решить важную задачу: выяснить среднюю ширину морды домашних котов нашей страны. Прямой способ, то есть измерение всех домашних питомцев, невозможен по ряду объективных причин. Придётся ограничиться выборкой — взять какое-то число животных, измерить морды именно им и сделать выводы по итогам только этих исследований.

Иллюстрация: Pixabay

Но тут сразу же возникают вопросы:

• Сколько и каких котов отобрать для замера?
• Почему именно этих, а не других?
• Какие есть гарантии, что вычисленное значение действительно будет средней шириной морды всех котов России?

Семплирование — это группа статистических методов и приёмов, отвечающих на эти вопросы. С помощью семплирования мы формируем нашу выборку так, чтобы она наилучшим образом отражала свойства генеральной совокупности — то есть свойства всех котов страны.

Качественная выборка сохраняет свойства всей генеральной совокупности

Иными словами, вы не можете измерить N первых попавшихся котов и обобщить результат для остальных. Выборка должна хорошо «сидеть» во всей популяции кошек, чтобы можно было делать обоснованные выводы. Такую выборку называют релевантной.

Кстати, статистика и котики — близнецы-братья. После выхода одноимённой книги Владимира Савельева мы говорим «статистика», а подразумеваем «котики», и наоборот. И смело рекомендуем эту книгу всем, кто дочитал до этого места.

В Data Science методы семплирования применяются при разработке, подготовке и оценке датасетов, чтобы они одновременно и были упорядоченными, и соответствовали реальности.

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Алгебра Координаты вектора как найти длину отрезка по двум точкам, правило и формула нахождения в пространстве, свойства, задачи с решением, онлайн-калькулятор

Диспе́рсия случа́йной величины́ — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается D[X] в русской литературе и \,X» width=»» height=»» /> (англ. variance ) в зарубежной. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии называется среднеквадрати́чным отклоне́нием, станда́ртным отклоне́нием или стандартным разбросом.

Заключение

Data Science — не просто комбинирование модных моделей в Jupyter-ноутбуке. Профессионалы в этой области глубоко понимают природу данных и то, как они могут помочь в принятии конкретных бизнес-решений.

Всё это изучалось в статистике задолго до того, как первый дата-сайентист набрал свой первый import pandas as pd. Статистика — фундамент всей современной науки о данных, включая машинное обучение, глубокие нейросети и даже искусственный интеллект.

В нашем курсе «Профессия Data Scientist» статистике уделено самое пристальное внимание. Вы не ударите в грязь лицом ни на тусовке статистиков, ни на настоящем DS-собеседовании

Приходите!