Начертательная геометрия тема 03

Прямая на плоскости — понятие.

Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).

Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости.

Теперь можно переходить и к понятию прямой линии на плоскости.

Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ

Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г).

Можно задать плоскость следами. Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Pv — фронтальный след плоскости Р, Рн — горизонтальный след плоскости Р, Pw — профильный след плоскости Р.

Различные случаи расположения плоскостей относительно плоскостей проекций

Плоскость общего положения — плоскость, расположенная наклонно ко всем плоскостям проекций (рис. 208). Такая плоскость пересекается с тремя плоскостями проекций по прямым, которые являются следами этой плоскости. Каждая пара следов сходится в точке, которая называется точкой схода следов плоскости и располагается на оси проекций. Плоскость общего положения имеет три точки схода, которые обозначаются Рх, Ру, Рz. В этих точках плоскость пересекает оси координат. Плоские фигуры, лежащие в плоскости общего положения, проецируются проекций с искажением.

Проецирующая плоскость — плоскость, перпендикулярная какой-либо плоскости проекций.

Горизонтально — проецирующая плоскость — плоскость, перпендикулярная горизонтальной плоскости проекций Н (рис. 209).

Фронтально — проецирующая плоскость — плоскость, перпендикулярная фронтальной плоскости проекции (рис. 210).

Профильно-проецирующая плоскость — плоскость, перпендикулярная профильной плоскости проекций (рис. 211).

Проецирующая плоскость проецируется на плоскость проекций, к которой она перпендикулярна, в прямую. Па рис. 209 плоскость Р горизонтально-проецирующая, ΔАВС, лежащий в плоскости Р, проецируется в отрезок прямой линии, который совпадает со следом плоскости Рн. На рис. 210 ΔDEF, принадлежащий фронтально-проецирующей плоскости R, проецируется в отрезок, совпадающий со следом плоскости Rv. На рис. 211 ΔKMN, лежащий в профильно-проецирующей плоскости Q, проецируется на плоскость W в отрезок, совпадающий со следом плоскости Qw. Поэтому проецирующие плоскости часто используются в качестве вспомогательных при различных построениях. Например, чтобы через прямую AB провести горизонтально-проецирующую плоскость (рис. 212), достаточно через горизонтальную проекцию прямой ab провести горизонтальный след этой плоскости, так как все, что в этой плоскости лежит, в том числе и прямая AB, проецируется на ее горизонтальный след. Фронтальный след фронтально-проецирующей плоскости совпадает с фронтальной проекцией прямой a’b’ (рис. 213). Следы проецирующих плоскостей на других плоскостях проекций перпендикулярны соответствующим осям проекций (см. рис. 209, 210, 211).

Рис. 212 Рис. 213

Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости проекций. Геометрические фигуры, лежащие в этих плоскостях, проецируются без искажения на ту плоскость проекций, которой параллельна данная плоскость (рис. 214, 215; 216). Называются такие плоскости так же, как и плоскость проекций, параллельно которой они расположены: горизонтальная плоскость (рис. 214), фронтальная плоскость (рис. 215), профильная плоскость (рис. 216).

Источник

Тема №3 Взаимное положение прямой и плоскости

Контрольные задания по теме:Рабочая тетрадь задача 39, задача 40а, задача 40б

Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).

Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).

Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).

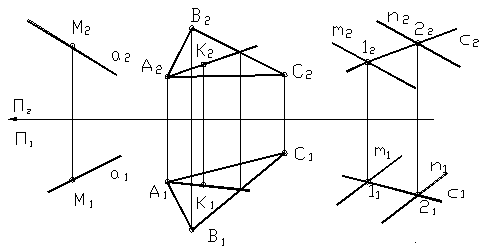Рисунок 21

Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (aÇb).

Рисунок 22

Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.

Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.

Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k ÇΣ (ABC) = K.

Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.

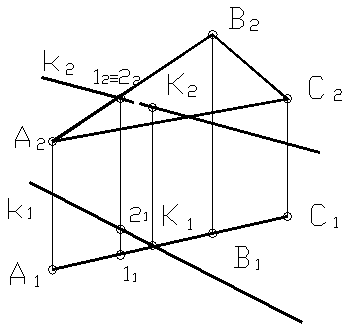Рисунок 23

Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.

t Î Σ ^ П₂ – прямая t принадлежит плоскости Σ, которая перпендикулярна горизонтальной плоскости проекций. Линия пересечения этой плоскости с данной — линия (1, 2). Затем находится точка пересечения этой линии с прямой t , которая и будет являться точкой встречи прямой и плоскости. Видимость прямой относительно плоскости определяется при помощи конкурирующих точек. Возьмем горизонтально конкурирующие точки 3 и 4. Так как точка 3, принадлежащая прямой, оказалась ниже чем точка 4, следовательно, прямая на горизонтальной плоскости справа от точки пересечения невидима. Затем берем фронтально конкурирующие точки 1 и 5. Точка 1, принадлежащая плоскости, лежит ближе, следовательно, прямая находится за плоскостью, и она на фронтальной проекции невидима от точки 1 до точки К.

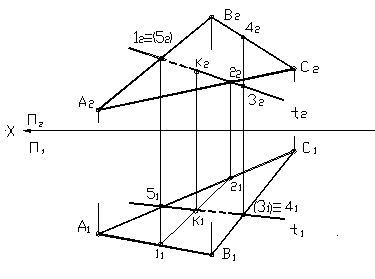Рисунок 24

К особым прямым, принадлежащим плоскости, относятся горизонталь, фронталь и профильная прямая. Построение этих прямых используется при решении многих задач по начертательной геометрии. Их изображение дано на рисунке 25. Причём на горизонтальной плоскости горизонталь имеет натуральную величину, на фронтальной плоскости — фронталь и на профильной плоскости – профильная прямая.

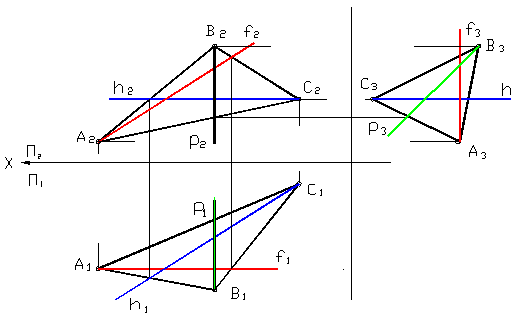Рисунок 25

1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.

2. Как построить прямую параллельную заданной плоскости?

3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.

4. Какие точки называются конкурирующими?

5. Как провести в плоскости горизонталь и фронталь?

6. Какие еще особые прямые плоскости вы знаете?

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

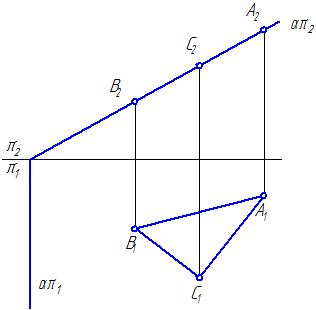
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

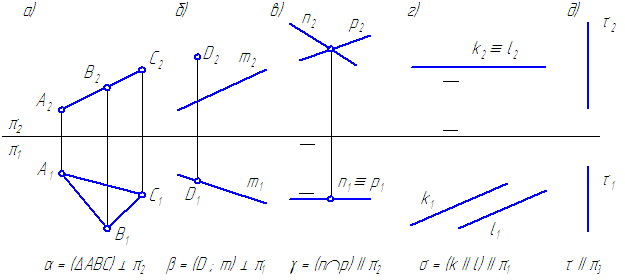
Рисунок 3.4 – Эпюры плоскостей частного положения

Прямые частного положения в плоскости

В каждой плоскости можно провести бесчисленное множество прямых линий частного положения. Рассмотрим некоторые прямые, лежащие в плоскости и занимающие относительно плоскостей проекций частные положения.

Горизонталь плоскости — это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций . Она обладает всеми свойствами горизонтальной прямой: ее фронтальная проекция параллельна оси , а на горизонтальную плоскость проекций она проецируется в истинную величину.

Построим любую горизонталь плоскости, заданной треугольником (рис.39). Фронтальную проекцию горизонтали получаем, построив (расстояние от оси выберем произвольно). Строим горизонтальные проекции точек и , и через и проводим горизонтальную проекцию горизонтали.

Если плоскость задана следами (рис.40), то горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Следует отметить одну интересную особенность горизонтальных проекций горизонталей плоскости: все они параллельны между собой и, поскольку они параллельны горизонтальному следу этой плоскости, положение любой из них определяет направление горизонтального следа плоскости.

Фронталь плоскости — это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали параллельна оси , а фронтальная проекция — ее истинная величина.

Пример построения фронтали плоскости, заданной треугольником , дан на рис.41 (построение выполнено аналогично построению горизонтали на рис.39).

В плоскости, заданной следами, фронтальная проекция фронтали параллельна фронтальному следу плоскости (рис.42).

Линия наибольшего ската — это прямая, лежащая в плоскости и перпендикулярная горизонталям этой плоскости. На рис.43 построена прямая , являющаяся линией наибольшего ската плоскости . Прямой угол между линией наибольшего ската плоскости и любой горизонталью этой плоскости проецируется на плоскость без искажения (на основании правил проецирования плоских углов). Следовательно, горизонтальная проекция линии наибольшего ската перпендикулярна горизонтальной проекции любой горизонтали или горизонтальному следу плоскости.

Из всех прямых, принадлежащих плоскости, линия наибольшего ската имеет самый большой угол наклона к горизонтальной плоскости проекций, который называется углом падения данной плоскости. В горно-геологической практике угол падения -это одна из важнейших характеристик изображаемого объекта (земной поверхности, пласта полезного ископаемого и т.п.).

Пример 6. Через точку построить линию наибольшего ската плоскости, заданной треугольником (рис.44).

1. Строим произвольную горизонталь плоскости треугольника .

2. Прямая является линией наибольшего ската плоскости треугольника , так как .

Рассмотренные нами прямые частного положения, лежащие в плоскости, главным образом горизонтали и фронтали, весьма часто применяют в различных построениях в качестве вспомогательных прямых.

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Решение

Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 )

Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Взаимное расположение плоскости и точки.

Начнем с аксиомы: в каждой плоскости имеются точки. Из нее следует первый вариант взаимного расположения плоскости и точки – точка может принадлежать плоскости. Другими словами, плоскость может проходить через точку. Для обозначения принадлежности какой-либо точки какой-либо плоскости используют символ «». Например, если плоскость проходит через точку А, то можно кратко записать .

Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.

Следующая аксиома показывает, сколько точек в пространстве необходимо отметить, чтобы они определяли конкретную плоскость: через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. Если известны три точки, лежащие в плоскости, то плоскость можно обозначить тремя буквами, соответствующими этим точкам. Например, если плоскость проходит через точки А, В и С, то ее можно обозначить АВС.

Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «», который равносилен фразе «не принадлежит».

К примеру, если точка А не лежит в плоскости , то используют краткую запись .

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

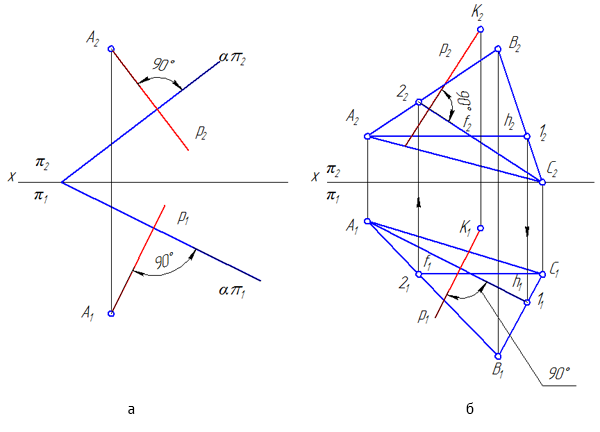
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

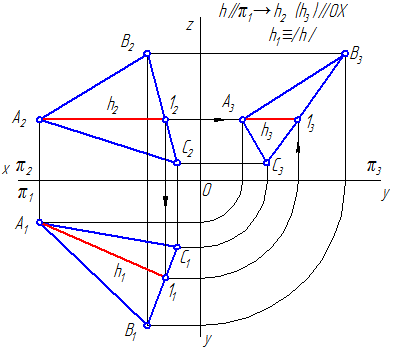
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂. Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций. Необходимо отдельно определить видимость на каждой плоскости проекций. Видимость на π₂ (рис. 3.15) Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF. Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂. Направление взгляда на π₂ показано стрелкой. По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁. 4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ. Видимость на π₁. Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5. Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁. Направление взгляда на π₁ показано стрелкой. По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂. 2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ. Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

Принадлежность точки прямой

Определимся, как выражать принадлежность точки прямой. Для этого рассмотрим на плоскости точки $C$, $D$, $F$, $G$ и прямые $a$, $b$. Точки $C$ и $D$ лежат на прямой $a$. Точка $G$ лежит на прямой $b$. С другой стороны, точки $F$ и $G$ не лежат на прямой $a$. То же самое можно сказать про точки $C$, $D$ и $F$ — они не лежат на прямой $b$.

Математические символыПринадлежность точки прямой обозначается символом «$\in$» и читается как «принадлежит». Например, $A\in{a}$ — «точка $A$ принадлежит прямой $a$». Для отсутствия принадлежности используется перечеркнутый символ «$\notin$». Например, $B\notin{c}$ — «точка $B$ не принадлежит прямой $c$».

{"questions":[{"content":"`image-1`Даны прямая $a$ и точки $A$ и $B$. Завершите ниже отношения принадлежности точек прямой, вписав соответствующие обозначения.`input-8` $\\in$ `input-18``input-44` $\\notin$ `input-66`","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/07/AB-test.svg"},"input-8":{"type":"input","inline":1,"answer":"A"},"input-18":{"type":"input","inline":1,"answer":"a"},"input-44":{"type":"input","inline":1,"answer":"B"},"input-66":{"type":"input","inline":1,"answer":"a"}},"step":1,"hints":["Точка $A$ принадлежит прямой $a$. В математической нотации: $$A\\in{a}$$","Точка $B$ не принадлежит прямой $a$. В математической нотации: $$B\\notin{a}$$"]}]}

Точки и прямые связаны отношениями принадлежности. Также вспомним, что прямая — абстрактный геометрический объект, состоящий из точек. Из этого мы можем сделать вывод, что на плоскости всегда будут точки, принадлежащие прямой, и точки, ей не принадлежащие. Это — одна из главных аксиом планиметрии.

Внимание. Аксиомы мы будем вымещать в рамочки и вести нумерацию «$A_x$», где $x$ — номер аксиомы

Давайте сформулируем нашу первую аксиому:

Точка и прямая: аксиома прямой

Мы говорили о том, что прямая — это совокупность точек, но ни разу не определили, сколько минимум нужно расположить точек на плоскости, чтобы задать строго одну прямую.

Предположим, что достаточно только одной точки. Рассмотрим, к примеру, точку $A$ и прямые $a$ и $b$. Как видим, через одну точку может проходить сколь угодно прямых.

Оставлять вопрос открытым нельзя. «Минимальные требования» к тому, сколько точек необходимо для проведения одной прямой, очень важны, ведь по сути они являются определением прямой.

Поэтому в планиметрии в данном отношении принята следующая аксиома:

Почему через две точки можно провести только одну прямую?

Во-первых, напомним, что аксиома — это прежде всего бездоказательный фундамент, поскольку ее «начинка» — здравый смысл. Смысл-то здравый, но почему через две точки можно провести только одну прямую? Это не кажется чем-то базовым, до чего догадается даже первоклассник.

Однако объяснение вполне прозаично. Давайте представим себе ситуацию с пересечением прямых. Пусть есть две прямые, которые пересекаются не в одной точке, а в двух. Давайте еще и не представлять, а чертить. Реален ли подобный чертеж выше?

Никак не реален. Если бы прямые имели две точки пересечения, они бы были уже не прямые, а изогнутые. Отсюда аксиома, говорящая, почему через две точки можно провести только одну прямую. И соответственно из нее следствие:

{"questions":,"answer":}}}]}

3.7. Перпендикулярность прямой плоскости

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

Что такое плоскость в геометрии?

Аналогия с конструктором-игрушкой, на самом деле, очень сподручна. И мы воспользуемся ей еще раз для того, чтобы рассмотреть, что такое плоскость в геометрии. Положим, вы купили набор в стиле «собери домик». Казалось бы, первым делом вы осмотрите схему сборки и детали. Однако… это не так. Первым делом вы освободите себе место на полу, где будет идти жилстроительство.

Определим плоскость математически:

Тем не менее, для правильного понимания, что такое плоскость в геометрии, сравнение «как место на полу» не стоит воспринимать буквально. Место на полу имеет физические ограничения. К тому же оно реально, — вы можете прикоснуться к поверхности пола в любой момент.

Давайте сравним. Плоскость в геометрии:

Абстрактна. Ее нельзя так же явственно представить, как реальный физический объект. Например, яблоко. Вы не можете ее сфотографировать или нарисовать.
Двухмерна. Построенный на плоскости пола домик из игрушечного набора является трехмерным. Плоскость в планиметрии задает фигуры без объема. Условно говоря, лишь их «очертания».
Не поддается измерению. Плоскость в геометрии нельзя измерить в длину или ширину как поверхность пола. Она бесконечна, она просто существует.

Абстрактные плоскости!

Вроде бы геометрические фигуры являются конкретными объектами мира, но вот начальная их стадия изучения, выходит, привязана к абстракциям. Просто помните, что во многом абстракция — это идея, и у идей нет формы. Задумайтесь: вся математика является воображаемой, ведь числа в действительности тоже не существует.

Число мы придумали как абстракцию, которая оказалась очень удобной для описания физически существующего. Плоскость в геометрии — еще одна удобная математическая идея, чтобы представить место, где бы располагались фигуры. Плоскость не в пример полу идеально ровная и идеально бесконечная. В общем-то наука полна абстрактных идей. Даже физика не исключение.

{"questions":[{"content":"Перечислим еще раз основные свойства плоскости. Выберите положения, которые соответствуют определению плоскости в геометрии. `speech-1``choice-5`","widgets":{"speech-1":{"type":"speech","text":"Небольшая подсказка: мы обсудили три положения."},"choice-5":{"type":"choice","options":,"answer":}}}]}

3.4. Главные линии плоскости

Плоскость – основные понятия, обозначения и изображение.

Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости. Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.

Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q, прямые а и d. Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В. Плоскости принято обозначать маленькими греческими буквами, например, плоскости , или .

При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.

Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.

Прямая на плоскости — понятие.

СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ

Тема №3 Взаимное положение прямой и плоскости

3.2. Плоскости частного положения

Прямые частного положения в плоскости

Неполное общее уравнение плоскости

Взаимное расположение плоскости и точки.

3.7. Перпендикулярность прямой плоскости

3.4. Главные линии плоскости

Общее уравнение плоскости, проходящей через точку

3.6. Определение видимости методом конкурирующих точек

Принадлежность точки прямой

Точка и прямая: аксиома прямой

Почему через две точки можно провести только одну прямую?

3.7. Перпендикулярность прямой плоскости

Что такое плоскость в геометрии?

3.4. Главные линии плоскости

Плоскость – основные понятия, обозначения и изображение.

Похожие записи:

Похожие записи: