Производная

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Конспект урока «Приращение аргумента, приращение функции»

· познакомиться с понятием непрерывной функции;

· познакомиться с понятием предел функции в точке;

· рассмотреть примеры использования данных понятий для решения задач.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются

Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит

Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.

Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.

Для описания таких изменений было введено понятие приращение.

Определение.

Пусть функция y = f(x) определена в точках x и x₁. Разность x₁ – x называют приращением аргумента, а разность f(x₁) – f(x) называют приращением функции.

Приращение аргумента обозначают так:

Приращение функции обозначают так:

Давайте рассмотрим, что же такое приращение аргумента и функции на графике.

Рассмотрим ещё один пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.

Определение непрерывности функции в точке x = a выглядит так:

Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка a; b.

Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

• Конспект занятия по рисованию вода в средней группе

    

• Музыкальные жанры 3 класс конспект

    

• Конспект родительского собрания 2 класс режим дня

    

• Телевизор конспект занятия в младшей группе

    

• Конспект внеклассного занятия по математике для развития интереса 2 класс

Проверь себя

Задание 1. Что такое приращение функции? 

1. Разность между значениями у;
2. Разность между значениями х;
3. Сумма значений у;
4. Сумма значений х. 

Задание 2. Чему равна производная?

1. Котангенсу угла наклона касательной;
2. Тангенсу угла наклона касательной;
3. Синусу угла наклона касательной;
4. Косинусу угла наклона касательной. 

Задание 3. Как меняется знак производной в точке максимума? 

1. Знак производной не меняется;
2. Производная всегда равна 0 и не имеет знака;
3. Знак меняется с положительного на отрицательный;
4. Знак меняется с отрицательного на положительный.

Задание 4. В каком случае функция будет возрастать? 

1. Если производная положительна;
2. Если производная отрицательна;
3. Если производная равна 0;
4. Ни один из вышеперечисленных случаев. 

Задание 5. Какая величина получится, если дважды взять производную у функции? 

1. Скорость;
2. Ускорение;
3. Путь;
4. Время

Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 1

Предел функции в точке

Порою нас интересует поведение функции не на бесконечности, а вблизи конкретной точки х. Конечно, в большинстве случае можно просто вычислить функцию в этой точке, однако иногда это невозможно сделать. Для примера рассмотрим функцию

Очевидно, что точка х = 2 не входит в ее область определения, ведь при подстановке этого значения в функцию знаменатель дроби обратится в ноль. Однако в любой другой точке значение функции будет равняться единице:

График такой функции будет выглядеть как прямая у = 1, у которой есть одна «выколотая точка», соответствующая х = 2:

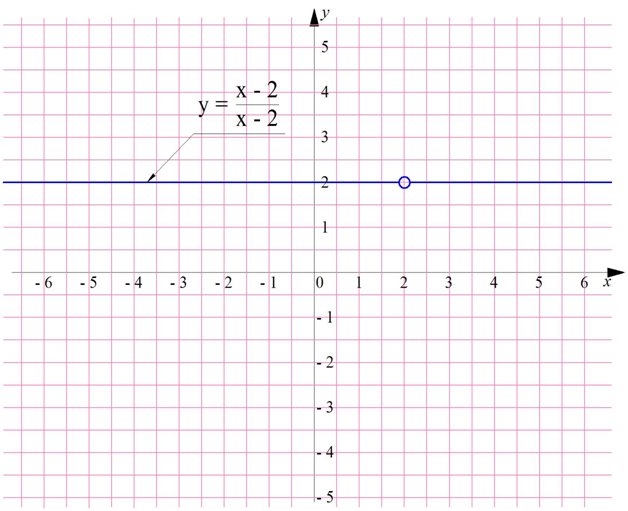
Итак, функция не определена в точке х = 2, однако можно вычислить предел функции в точке х = 2. Действительно, при любом, сколь угодно близком к 2 значении х функция будет равна единице:

Попробуем также приблизиться к точке 2 с другой стороны, подставляя в функцию числа, меньшие двух:

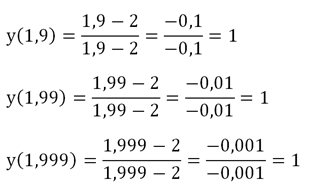
Снова всё время получается единица. Поэтому мы можем уверенно записать, что

Значительно чаще приходится иметь дело с пределами в точке, которые равны бесконечности. Снова посмотрим на график функции у = 1/х:

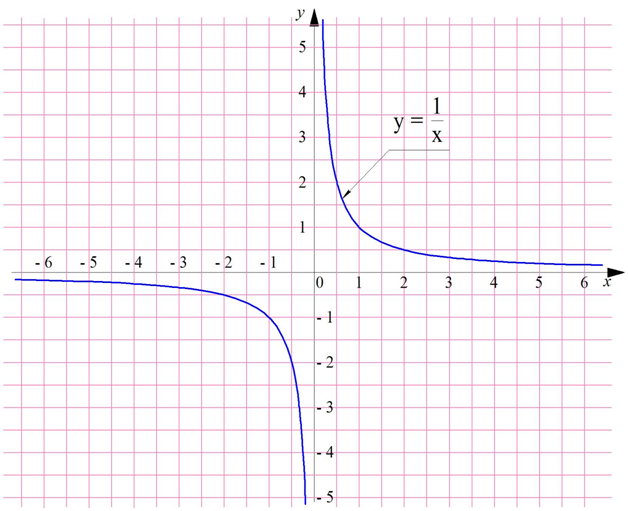
Видно, график не пересекает ось Оу, ведь число х = 0 не входит в область определения функции. Однако можно заметить, что при приближении х к нулю функция неограниченно возрастает:

Обратите внимание, что под пределом мы использовали запись «х → + 0», а не «х → 0». Почему? Дело в том, что если мы будем приближаться к нулю с «противоположной» стороны, подставляя в функцию не положительные, а отрицательные числа, то функция будет стремится к – ∞:

Получается, что предел функции в точке х = 0 зависит от того, с какой стороны мы приближаемся к этой точке, слева или справа. В связи с этим в математике существует понятие односторонних пределов. Для обозначения пределов, получаемых при приближении к нулю справа, то есть со стороны бОльших чисел, перед ним ставят знак плюс, а при указании предела слева, то есть со стороны мЕньших чисел – знак минус:

Предел и односторонние пределы – это два разных понятия. Считается, что функция имеет предел в точке только тогда, когда оба односторонних предела в этой точке совпадают.

В качестве ещё одного примера предела функции в точке можно привести зависимость , график которой выглядит следующим образом:

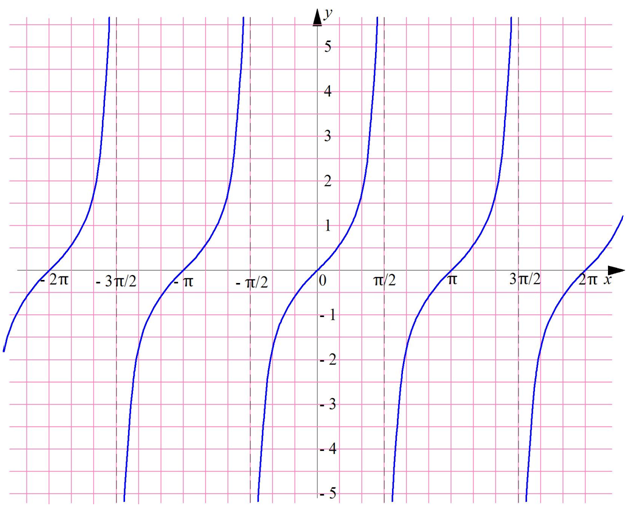
В точке х = π/2 функция не определена. Однако видно, что при приближении к этой точке слева функция неограниченно возрастает, а при приближении справа – неограниченно убывает. Это записывается следующим образом:

До этого мы вычисляли пределы функций в точках, где сами функции не определены. Однако пределы можно вычислять и в тех точках, где функция определена. В большинстве случаев (но не всегда) они как раз равны значению функции в этой точке. Например, найдем предел

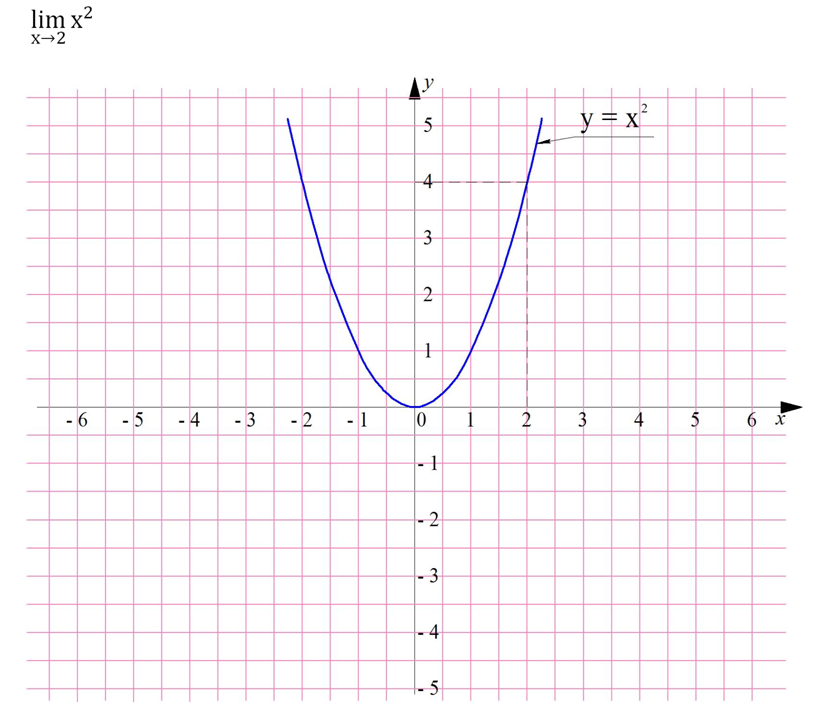
В точке х = 2 значение функции будет равно 4:

Будут ли односторонние пределы в этой точке также равняться 4? Сначала проверим предел справа

Действительно, получаем значения у, всё более близкие к 4. Аналогично можно убедиться, что и предел слева также равен 4:

Приведем несколько искусственный пример функции, у которой предел в точке не совпадает со значением функции в этой точке. Пусть функция задается с помощью такого графика

Он представляет собой параболу у = х2 с выколотой точкой (2; 4). При этом функция определена в точке х = 2, но имеет там значение, равное единице. Аналитически эту функцию можно описать так:

Понятно, что у(2) = 1, однако попытаемся приблизиться к точке х = 2 справа и слева и посмотрим, что получится:

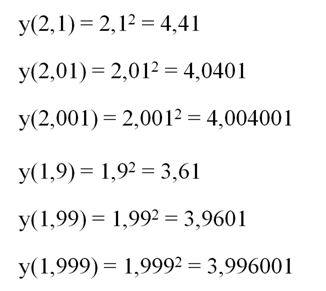
Мы видим, что при х→2 функция и справа, и слева стремится к четверке, а не к единице. То есть получается, что предел функции в точке х = 2 не совпадает со значением функции этой функции в этой же точке. Такая ситуация произошла именно из-за того, что точка х = является выколотой.

Сразу заметим, что непосредственно в практических задачах пределы почти не используются. В связи с этим эта тема изучается в школьном курсе довольно поверхностно, не дается строгое определение предела функции (предполагается, что это понятие интуитивно понятно), а также не рассматриваются примеры на вычисление пределов функций. С другой стороны, на понятии предела построены почти все строгие рассуждения и доказательства в математическом анализе. В частности, определение понятие производной (которая имеет огромное практическое применение) дается именно с помощью предела. Поэтому полностью исключить пределы из школьного курса нельзя.

Производная

Функции достаточно часто встречаются при решении задач. Они могут быть как составными частями какого-то задания, так и отдельным номером. Разумеется, встречаются не только простые функции. Если открыть банк заданий, то мы удивимся, насколько сложными они бывают. Так что делать с такими сложными и непонятными функциями? 

Производная — одно из самых важных понятий математического анализа. С ее помощью можно описать поведение любой функции. 

Почему функции похожи на американские горки? Предположим, мы хотим прокатиться на американских горках. Представим их вид сбоку: это череда подъемов и резких спусков. Мы можем с легкостью описать их: на каких участках будет подъем, а на каких спуск, насколько крутыми они будут, сколько раз вагончик преодолеет границу между подъемом и спуском или спуском или подъемом. Мы даже можем предположить, на каких участках вагончик разгоняется сильнее. Точно так же можно описать и любую функцию.

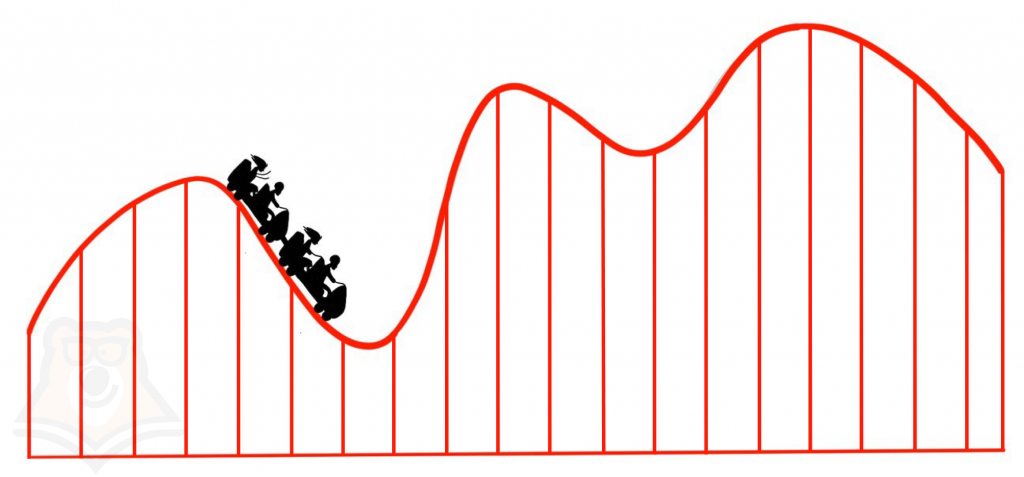
Представим наши американские горки в виде функции. 

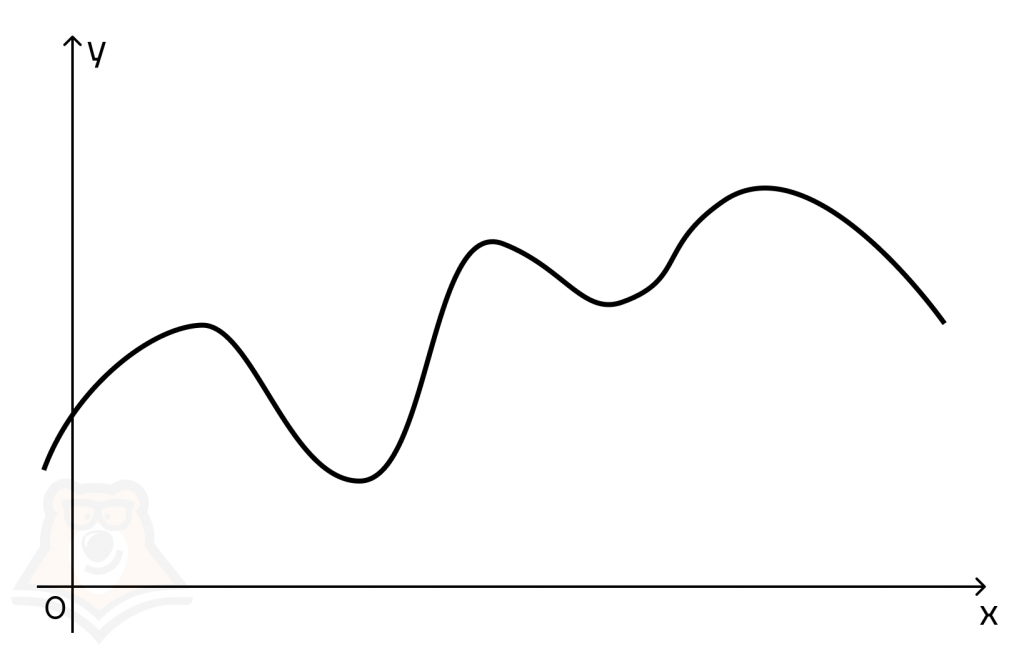
Функция будет на некоторых участках возрастать, а на некоторых убывать. Скорость ее изменения на разных участках будет разной. 

Скорость изменения функции показывает, насколько сильно будет изменяться значение функции (то есть значение у) при небольшом изменении переменной функции (то есть значения х). 

Отложим на нашем графике две точки: х и х₁ и поднимем из них прямые, которые пересекут график в точках А и В. Тогда точка А будет иметь координаты (х;у), а точка В — (х₁;у₁). 

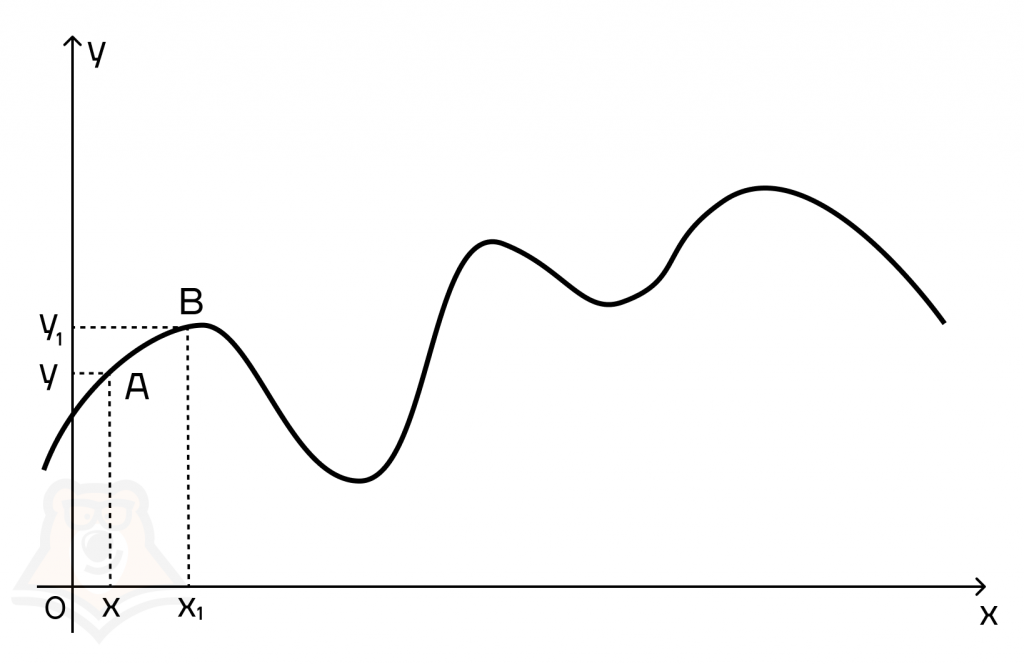
Представим, что наш вагончик проехал из точки А в точку В. Расстояние, которое он проехал по горизонтали, будет равно х₁ — х, а поднялся он на высоту у₁ — у. Для удобства дальнейших рассуждений примем эти расстояния за х и у. 

Знак Δ “дельта” — означает изменение величины, то есть разность между тем, что было в точке А и стало в точке В.

Теперь мы можем ввести определение приращения. 

Приращение функции — это разность между двумя значениями функции, то есть у.

Приращение аргумента — это разность между двумя значениями аргумента, то есть х.

Скорость изменения функции будет равна отношению приращения функции к приращению аргумента. При этом чем меньше будет приращение аргумента, тем точнее мы приблизимся к верному значению. 

Отсюда мы получаем определение производной функции. 

Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции. 

Производную функции обозначают как f'(x). 

\(f'(x) = \frac{\Delta y}{\Delta x}\: при\: \Delta x \rightarrow 0\)

Если мы применим одинаковое приращение аргумента к разным участкам функции, то заметим, что приращение функции также будет разное. Где-то значение у изменится больше, где-то меньше. Именно так изменяется скорость функции на разных ее участках. 

Нахождение производной называется дифференцированием. 

Как с помощью производной оценить рост популярности видео в соцсети?Допустим, мы выложили видео в соцсеть. Сначала было совсем невесело: за первый час всего один просмотр. За второй час ситуация сильно не изменилась — добавилось лишь 3 просмотра. Мы скинули ссылку на видео в чат друзей, и за третий час количество просмотров дошло до 9, а за четвертый час — до шестнадцати. Возможно, ситуация не очень похожа на правду, и мы бы сразу попали в топ. Но пусть будет так для удобства цифр. В результате мы имеем функцию, которая показывает, как количество просмотров менялось во времени. 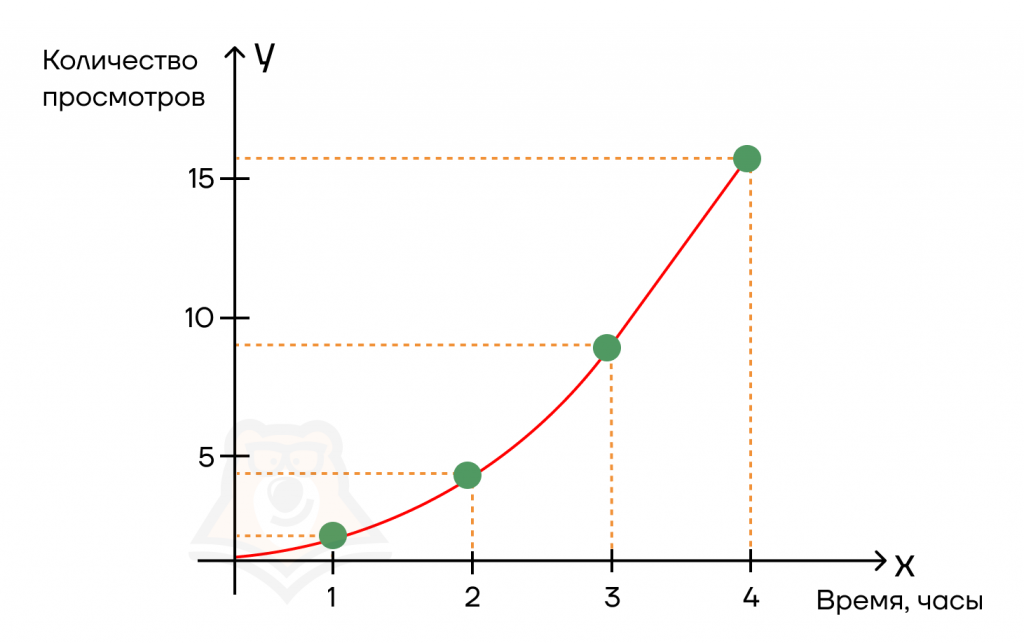Теперь зададимся вопросом: как быстро росла популярность у нашего ролика?Чтобы это выяснить, мы возьмем две соседние точки на графике и посчитаем:1) как изменилось количество просмотров между этими точкам (Δ количества просмотров);2) как изменилось время между этими точками (Δ времени);3) затем разделим Δ просмотров на Δ времени.Получается, что “производительность” нашего видео была 5 просмотров в час. Таким нехитрым образом, мы нашли производную от функции, показывающую рост популярности нашего ролика в сети за определенный промежуток времени:\(f'(x) = \frac{\Delta y}{\Delta x} = \frac{5}{1} = 5\)(просмотров в час)

Предел функции на бесконечности

Рассмотрим довольно простую функцию

y = 1/x

Её график называется гиперболой и выглядит так:

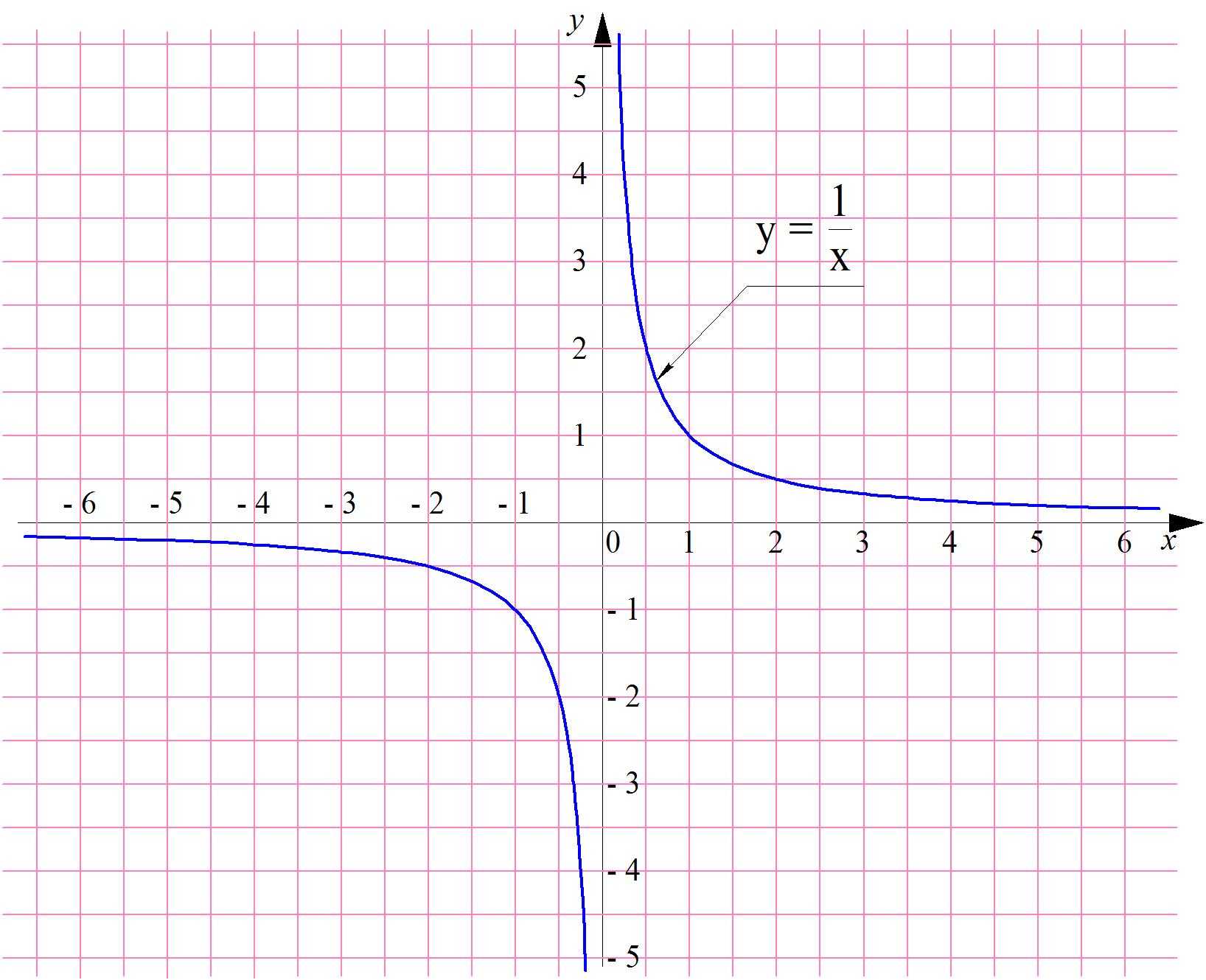
Можно заметить, что при больших положительных значениях х график функции приближается к горизонтальной оси Ох, но не пересекает её. Действительно, если мы будем вычислять значение у при всё больших значениях х, то будем получать всё меньшие, но всё же положительные числа:

Получается, что при бесконечном росте аргумента х функция стремится к нулю. Можно ли эту особенность функции как-то записать, используя математические символы? Оказывается, можно, и выглядит это запись так:

которая означает, что х стремится к бесконечности. После символа lim записана сама функция 1/х. В целом вся запись читается так: «предел функции у = 1/х при х, стремящемся к бесконечности, равен нулю».

Вернемся к графику функции у = 1/х. Видно, что если мы будем брать всё меньшие отрицательные значения х, то функция также будет стремится к нулю. Действительно, попробуем подставлять в нее как можно меньшие значения аргумента:

Чтобы записать эту особенность функции, используется следующая запись:

который может быть получен параллельным переносом графика у = 1/х на две единицы вверх:

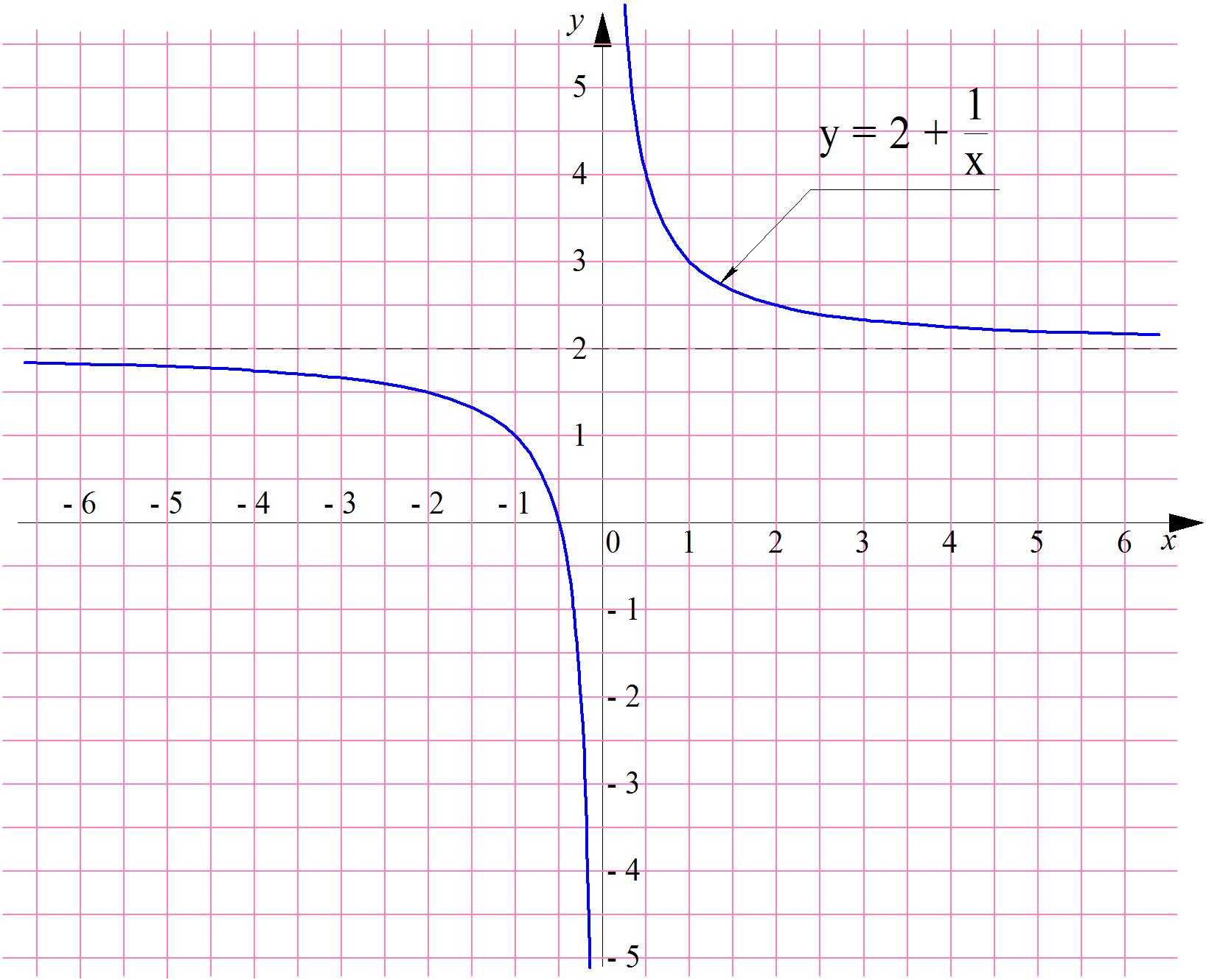
Очевидно, что пределы этой функции при х → + ∞ и х → – ∞ равны 2:

Возможны случаи, когда при бесконечном увеличении аргумента функции она не стремится к какому-то конкретному числу, а сама также неограниченно возрастает. Для примера посмотрим на график :

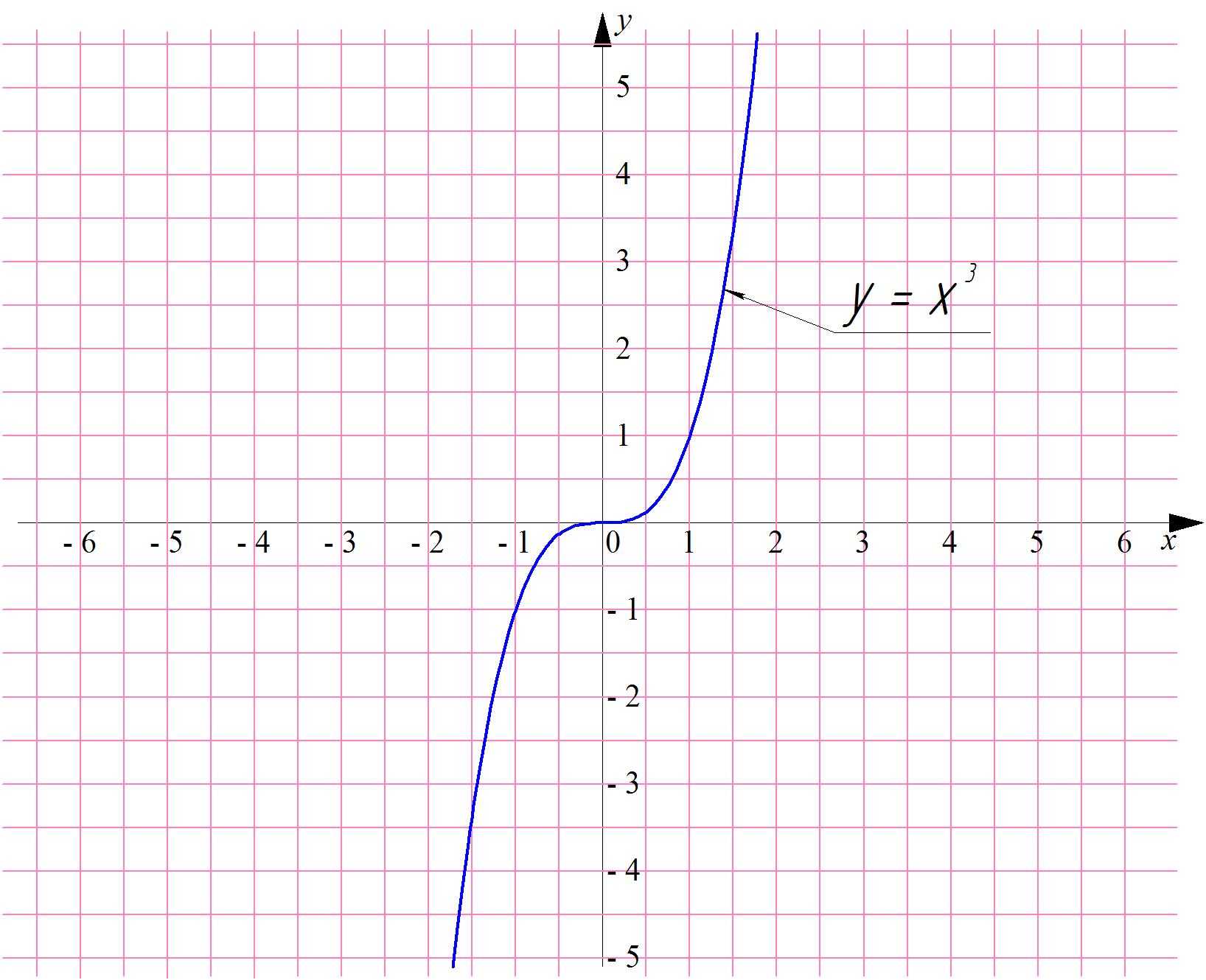
Видно, что при х → ∞ сама функция неограниченно растет, что можно показать расчетами:

Возникает вопрос – для всякой ли функции можно указать ее предел на бесконечности? Оказывается, что нет. Для примера рассмотрим у = sinx, графиком которой является синусоида:

С одной стороны, sinx явно не стремится к какому-то конкретному числу при увеличении х, он «колеблется» между числами 1 и (– 1). С другой стороны, нельзя и сказать, что он стремится к бесконечности. Получается, что у этой функции просто нет пределов на бесконечности.