Работа и переменные силы

Содержание

Слайд 1
Слайд 2

Работа переменной силы при поступательном движении
Работа при вращательном движении
Кинетическая и поступательная энергии при поступательном движении
Кинетическая энергия вращательного движения
Основной закон механики
Слайд 3

A = F∙ x =
x – перемещение
Работа при вращательном движении твердого тела. Рассчитаем работу силы, вызывающей вращательное движение тела вокруг некоторой оси и приложенной к произвольной точке этого тела. Согласно определению работы имеем:
dA = F·ds = Ft·ds.
Поскольку ds = r·da, то получим следующее выражение для работы:
dA = Ft·r·da = M·da.
При вращательном движении твердого тела под действием силы F работа равняется произведению момента этой силы на угол поворота.
Работа переменной силы при повороте тела на конечный угол равняется определенному интегралу от момента сил:
Слайд 4

Кинетическая энергия твердого тела, совершающего вращательное и поступательное движения. Любое произвольное движение твердого тела можно представить в виде суммы поступательного движения центра масс тела и вращательного движения в СО, связанной с этим центром масс. Проанализируем движение тела относительно двух таких систем: СО, связанной с центром масс тела — точкой С, и инерциальной СО — системой XY, относительно которой перемещается центр масс. Любая точка тела участвует в двух движениях: поступательном, происходящим в данный момент времени со скоростью Vc, и вращательном, происходящим с угловой скоростью w’ = vi’/Ri, относительно точки С.
Скорости тела в этих системах связаны между собой известным соотношением:
vi = Vc + vi’, гдеvi — скорость iой части в ИСО;Vc — скорость движения центра масс тела;vi’ — скорость iой части в СО, связанной с центром масс.
кинетическая энергия твердого тела состоит из кинетической энергии его поступательного движения и энергии его движения E’ = I·w2/2 относительно СО, связанной с центром масс тела. Это утверждение называется теоремой Кёнига.Eк = E’ + M·Vc2/2.
Теорема Кёнига справедлива для любого плоского движения при котором центр масс перемещается в некоторой фиксированной плоскости, а вектор угловой скорости все время перпендикулярен к этой плоскости. Примером плоского движения является качение.
Слайд 5

Теорема Штейнера.
Момент инерции тела относительно произвольной оси вращения равен его моменту инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы на квадрат расстояния между этими осями.
I = Ic + m·d2/2.
Слайд 6

Основные законы механики.
ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЭНЕРГИИ — общий закон природы: энергия любой замкнутой системы при всех процессах, происходящих в системе, остается постоянной (сохраняется). Энергия может только превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение (уменьшение) ее энергии равно убыли (возрастанию) энергии взаимодействующих с ней тел и физических полей.
ЗАКОН АРХИМЕДА — закон гидро- и аэростатики: на тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх, числено равная весу жидкости или газа, вытесненного телом, и приложенная в центре тяжести погруженной части тела. FA= gV, где r — плотность жидкости или газа, V — объем погруженной части тела. Иначе можно сформулировать так: тело, погруженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость (или газ). Тогда P= mg — FA
Слайд 7

ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ — закон тяготения Ньютона: все тела притягиваются друг к другу с силой прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними:

где M и m — массы взаимодействующих тел, R — расстояние между этими телами, G — гравитационная постоянная (в СИ G=6,67.10-11 Н.м2/кг2).
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ, механический принцип относительности — принцип классической механики: в любых инерциальных системах отсчета все механические явления протекают одинаково при одних и тех же условиях.
ЗАКОН ГУКА — закон, согласно которому упругие деформации прямо пропорциональны вызывающим их внешним воздействиям.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА — закон механики: импульс любой замкнутой системы при всех процессах, происходящих в системе, остается постоянным (сохраняется) и может только перераспределяться между частями системы в результате их взаимодействия.

Посмотреть все слайды

Работа постоянной силы

Предположим, что на мобильный телефон при перемещении по модулю d действует постоянная сила интенсивности F, наклоненная по отношению к направлению перемещения.

По определению работают (Т) под действием постоянной силы F вдоль смещения d определяется выражением:

Т = F · d · cos θ

В этом выражении F силовой модуль, d модуль смещения и θ, угол между векторами F и d. В Международной системе (СИ) единицей силы является Ньютон (N), единицей смещения является метр (м) а рабочая единица — это джоуль (Дж).

instagram stories viewer

В зависимости от угла θ между векторами F и d работа, совершаемая силой, может быть положительный, ноль или же отрицательный, в соответствии с характеристиками, описанными ниже.

1. Если θ равно 0 ° (сила и смещение имеют одинаковый смысл), то cos θ = 1. В этих условиях:

Т = F · d

2. Если 0 ° ≤ θ <90 °, то cos θ> 0. В этих условиях работа положительна (T> 0) и называется моторная работа.

3. Если θ = 90 °, то cos θ = 0. В этих условиях работа нулевая (T = 0), или сила не работает.

4. Если 90 ° тяжелая работа.

5. Если θ равно 180 ° (сила и смещение имеют противоположные направления), то cos θ = –1. В этих условиях:

T = –F · d

Обратите внимание, что работы:

это всегда сила;
это зависит от силы и смещения;
он положительный, когда сила способствует перемещению;
он отрицательный, когда сила противодействует смещению;
его модуль максимален, когда угол между вектором смещения и вектором силы равен 0 ° или 180 °.
его модуль минимален, когда сила и смещение перпендикулярны друг другу.

Уравнение связи потенциальной силы с потенциальной энергией

1. Связь между потенциальной энергией и силой. Потенциальная энергия тяготения и упругих деформаций.

Пространство, в котором действуют консервативные силы, называется потенциальным полем. Каждой точке потенциального поля соответствует некоторое значение силы F, действующей на тело, и некоторое значение потенциальной энергии U. Значит, между силой F и U должна быть связь , с другой стороны, dA = –dU, следовательно Fdr=-dU, отсюда:

Проекции вектора силы на оси координат:

Вектор силы можно записать через проекции: , F = –grad U, где .

Градиент – это вектор, показывающий направление наибыстрейшего изменения функции. Следовательно, вектор направлен в сторону наибыстрейшего уменьшения U.

Потенциальная энергия упругой деформации (пружины)

Найдём работу, совершаемую при деформации упругой пружины. Сила упругости Fупр = –kx, где k – коэффициент упругости. Сила непостоянна, поэтому элементарная работа dA = Fdx = –kxdx. (Знак минус говорит о том, что работа совершена над пружиной). Тогда , т.е. A = U1 – U2. Примем: U2 = 0, U = U1, тогда .

На рис. 5.5 показана диаграмма потенциальной энергии пружины.

Рис. 5.5 Здесь E = K + U – полная механическая энергия системы, К – кинетическая энергия в точке x1.

Потенциальная энергия при гравитационном взаимодействии

Работа тела при падении A = mgh, или A = U – U0. Условились считать, что на поверхности Земли h = 0, U0 = 0. Тогда A = U, т.е. A = mgh.

Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга, потенциальную энергию можно найти по формуле .

На рис. 5.4 изображена диаграмма потенциальной энергии гравитационного притяжения масс M и m.

Рис. 5.4 Здесь полная энергия E = K + E. Отсюда легко найти кинетическую энергию: K = E – U.

2. Цикл Карно. Теорема Карно.

3. С какой скоростью V движется частица, если ее полная энергия в два раза больше энергии покоя?

4. Объем моля идеального газа с показателем адиабаты γ изменяют по закону V = a/T, где а – постоянная. Найти количество тепла, полученное газом в этом процессе, если его температура изменилась на ΔT.

По какой формуле вычисляется кинетическая энергия

Тела, которые перемещаются, так же могут совершить работу. К примеру, движущийся поршень сжимает расположенный в цилиндре газ, снаряд при движении пробивает мишень. Таким образом, у движущихся тел есть запас энергии, которую называют кинетической. Данная величина определяется массой тела и его скоростью:

Записанное равенство является следствием из преобразования следующих формул:

Работа A = FS
Сила F = ma.

Путем подстановки выражения силы в уравнение работы получим:

A = maS

Известно, что:

Таким образом:

где — кинетическая энергия, характерная для тела в первом состоянии,

— кинетическая энергия, характерная для тела во втором состоянии.

Теорема о кинетической энергии справедлива независимо от характера сил, оказывающих воздействие на тело. Как правило, различают кинетическую силу поступательного и вращательного движения. Являясь физической величиной, представляющей собой функцию скорости, кинетическая энергия определяется следующими факторами:

внутренняя природа рассматриваемого объекта;
отношения между объектом и наблюдателем (в физике наблюдатель формально определяется инерциальной системой отсчета).

Кинетическая энергия деградирует и сохраняется в каждой трансформации. При этом утрачивается ее способность совершать новые трансформации. Однако кинетическую энергию нельзя создать или разрушить. Она может быть только трансформирована, поэтому ее сумма во вселенной всегда является постоянной величиной. Кинетическая энергия частицы или твердого тела уменьшается до нулевого значения, когда данные объекты не вращаются и останавливаются. С другой стороны, системы, содержащие множества частиц, движущихся независимо, не совсем верно рассматривать по такому принципу. Для твердого вращающегося тела, полная кинетическая сила может быть разбита на две суммы:

энергия перемещения, которая связана со смещением центра масс тела в пространстве;
энергия вращения (с вращательным движением с определенной угловой скоростью).

2.3.2. Энергия

1. Наиболее общим определением понятия энергии можно считать то, которое связано с понятием состояния системы (или тела). Энергия всегда является функцией состояния системы (тела). В любом состоянии система имеет определенное значение энергии и может сохранять это состояние, а значит и энергию этого состояния, сколь угодно долго. Для перехода системы (тела) в другое состояние должна быть совершена работа.

Физическая величина, характеризующая способность тела или системы тел совершить работу, называется энергией.

Состояние системы (тела) может меняться в процессе движений. Формы движений в природе различны. Для количественного сравнения разных форм движений и служит понятие энергии. Поэтому можно дать другое определение для энергии.

Энергией называется физическая величина, являющаяся общей мерой различных форм движения материи.

Различают виды энергии механическую, внутреннюю, электромагнитную, химическую, ядерную и т.д.

Механическая энергия может быть обусловлена или движением тела с некоторой скоростью (кинетическая энергия), или расположением данного тела в системе других тел определенной конфигурации (потенциальная энергия) W_мех. = W_кин. + W_пот..

Пример упражнения

Блок скользит по плоскости с наклоном 37 ° с горизонталью под действием трех сил, как показано на следующем рисунке.

Учитывая sin 37 ° = cos 53 ° = 0,60 и cos 37 ° = = sin 53 ° = 0,80, определите работу каждой из сил при перемещении AB на 10 м и результирующую работу над телом.

разрешение

Где T = F · d · cos θ, имеем:

Для силы 100 Н угол θ между силой и перемещением AB составляет 53 ° (90 ° — 37 °):Т₁₀₀ = F · d_AB · Cos 53rdТ₁₀₀ = 100 · 10 · 0,60Т₁₀₀ = 600 Дж (двигатель)
Для силы 80 Н угол θ между силой и перемещением AB равен 90 °:Т₈₀ = F · d_AB · Cos 90 °Т₈₀ = 80 · 10 · 0Т₈₀ = 0 Дж (ноль)
Для силы 20 Н угол θ между силой и перемещением AB составляет 180 °:Т₂₀ = F · d_AB · Cos 180 °Т₂₀ = 20 · 10 · (–1)Т₂₀ = –200 Дж (стойкое)
Полученная работа будет алгебраической суммой всех работ:Т_р = T₁₀₀ + Т₈₀ + Т₂₀Т_р = 600 + 0 – 200Т_р = 400 Дж

За: Даниэль Алекс Рамос

Работа переменной силы

В предыдущем пункте для вычисления работы постоянной силы мы использовали уравнение T = F · d · cos θ. Однако есть другой способ рассчитать эту работу, используя для этого графический метод. Затем у нас есть график постоянной силы F как функции произведенного смещения.

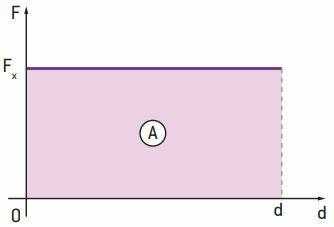
Обратите внимание, что область THE прямоугольника, указанного на рисунке, задается как A = FИкс · D, то есть работа численно равна площади фигуры, образованной кривой (линией графика) с осью смещения, в рассматриваемом интервале. Итак, мы пишем:. T = Площадь

T = Площадь

Мы можем применить это графическое свойство в случае силы с переменным модулем, чтобы вычислить работу, совершаемую этой силой. Учтите, что сила F изменяется в зависимости от смещения, как показано на следующем графике.

Площадь, обозначенная буквой A₁ обеспечивает работу силы F при перемещении (d₁ — 0), а область, обозначенная буквой A₂ обеспечивает работу силы F при перемещении (d₂ — d1). Как область А₂ лежит ниже оси смещения, работа силы в этом случае отрицательная. Таким образом, полная работа силы F при перемещении от 0 до d₂, определяется разностью площадей A₁ и площадь А₂.

Т = А1 — А2

НаблюдениеБудьте осторожны, не используйте знак минус дважды. Совет для решения этой ситуации состоит в том, чтобы вычислить две области по модулю, а затем определить разницу между площадью над осью d и площадью под осью d.

2.3.7. Применение законов сохранения в теории ударов тел

Ударом называется явление конечного изменения скоростей твердых тел за весьма малый промежуток времени при их столкновении.

Поведение соударяющихся тел можно рассчитать с помощью законов сохранения. Потенциальная энергия взаимодействующих тел не учитывается.

Абсолютно неупругий удар — удар, в результате которого тела после столкновения двигаются с одинаковыми скоростями. Поведение тел при таких ударах может быть описано моделью, называемой абсолютно неупругое тело.

Рассмотрим центральный неупругий удар двух шаров массой m₁ и m₂. Скорости шаров лежат на одной линии, соединяющей их центры: v₁и v₂— скорости шаров до удара, v — общая скорость шаров после удара. ЗСИ в векторной форме имеет вид:

m₁∙ v₁ + m₂∙ v₂ = ( m₁ + m₂)∙ v

Если v₁и v₂имеют одинаковые направления, то ЗСИ примет вид:

m₁∙ v₁ + m₂∙ v₂ = ( m₁ + m₂)∙v.

Если шары двигаются навстречу друг другу, тогда

m₁∙ v₁ — m₂∙ v₂ = ( m₁ + m₂)∙v

Закон сохранения механической энергии при таком ударе не выполняется, но с учетом энергии, затраченной на деформацию тел, общий закон сохранения энергии имеет вид:

Абсолютно упругий удар — такое кратковременное взаимодействие тел, при котором в обоих взаимодействующих телах не остается никаких деформаций. Поэтому кинетическая энергия, которой тела обладали до взаимодействия, превращается в кинетическую энергию тех же тел после взаимодействия.

Поведение тел при таких ударах может быть описано моделью, называемой абсолютно упругое тело.

Рассмотрим центральный упругий удар двух шаров массой m₁ и m₂. Скорости шаров лежат на одной линии, соединяющей их центры: v₁и v₂— скорости шаров до удара, u₁и u₂— скорости шаров после удара.

(ЗСИ) m₁∙ v₁ + m₂∙ v₂ = m₁∙ u₁ + m₂∙ u₂

( ЗСЭ_мех)

В ЗСИ надо учитывать направления скоростей до удара. Значения и направления скоростей после удара получаются при решении приведенной выше системы двух уравнений.

итоговая или полная работа

Исследуемые объекты (частицы, блоки и т. Д.) Могут подвергаться действию набора сил, которые действуют одновременно во время заданного смещения. В качестве примера рассмотрим следующий рисунок, на котором показан блок под действием четырех постоянных сил F₁, F₂, F₃ и F₄, во время смены d.

Работа, возникающая в результате одновременного действия четырех сил, может быть выполнена двумя способами, описанными ниже.

Рассчитываем работу каждой силы индивидуально (не забывая знак) и производим алгебраическую сумму всей работы:

Т_р = T₁ + Т₂ + Т₃ + Т₄

Рассчитываем чистую силу и применяем определение работы:

Т_р = F_р · D · cos θ

НаблюдениеЕсли есть переменные силы модуля, мы будем использовать исключительно первый режим (алгебраическая сумма).